L'altare di Betel

Centrale, nell'intera Tanakh, è il tema del Tempio di Gerusalemme, e nel Tempio, oltre altre al Santo dei Santi, c'è anche l'Altare. Impossibile dunque non dedicare una lezione ad esso, per trarne spunto per i nostri calcoli. La parola "altare" appare 361 volte nell'Antico Testamento e 23 nel Nuovo. I primi ad erigere un'ara al Signore per compiere un sacrificio in Suo onore sono Caino e Abele, anche se non pronunciano mai la parola "altare":

« Dopo un certo tempo, Caino offrì frutti del suolo in sacrificio al Signore; anche Abele offrì primogeniti del suo gregge e il loro grasso. » (Genesi 4, 3-4a)

Anche Noè compie un sacrificio a Dio, appena finito il diluvio, come segno della rinnovata alleanza tra Iddio e l'umanità:

« Allora Noè edificò un altare al Signore; prese ogni sorta di animali mondi e di uccelli mondi e offrì olocausti sull'altare. » (Genesi 8, 20)

Viene poi il turno di Abramo, appena arriva nella Terra Promessa cui il Signore lo ha indirizzato:

« Il Signore apparve ad Abramo e gli disse: "Alla tua discendenza io darò questo paese". Allora Abramo costruì in quel posto un altare al Signore che gli era apparso. » (Genesi 12, 7)

Anche Giacobbe innalza un altare a Dio in Betel, che non a caso significa "Casa del Signore" (sede di uno dei due santuari nazionali del regno settentrionale d'Israele, fatto risalire indietro nel tempo fino al patriarca Giacobbe):

« Dio disse a Giacobbe: "Alzati, va' a Betel e abita là; costruisci in quel luogo un altare al Dio che ti è apparso quando fuggivi Esaù, tuo fratello." » (Genesi 35, 1)

Mosè non può essere da meno, dopo che il popolo ebraico è stato liberato dalla schiavitù, ed infatti il Signore gli dice:

« Farai per me un altare di terra e, sopra, offrirai i tuoi olocausti e i tuoi sacrifici di comunione, le tue pecore e i tuoi buoi; in ogni luogo dove io vorrò ricordare il mio nome, verrò a te e ti benedirò. » (Esodo 20, 24)

Anche Giosuè fa la stessa cosa, una volta entrato nella sospirata Terra Promessa:

« In quell'occasione Giosuè costruì un altare al Signore, Dio di Israele, sul monte Ebal, secondo quanto aveva ordinato Mosè, servo del Signore, agli Israeliti, come è scritto nel libro della legge di Mosè » (Giosuè 8, 30-31)

Gedeone, all'epoca dei Giudici, non si limita a costruire un altare al Dio d'Israele, ma prima distrugge quello di Baal:

« In quella stessa notte il Signore gli disse: "Prendi il giovenco di tuo padre e un secondo giovenco di sette anni, demolisci l'altare di Baal fatto da tuo padre e taglia il palo sacro che gli sta accanto. Costruisci un altare al Signore tuo Dio sulla cima di questa roccia, disponendo ogni cosa con ordine; poi prendi il secondo giovenco e offrilo in olocausto sulla legna del palo sacro che avrai tagliato." » (Giudici 6, 25-26)

Non è da meno il Giudice Samuele, che la sua ara la edifica nella sua città natale di Rama di Beniamino, oggi Er-Ram, circa 8 km a nord di Gerusalemme:

« Poi ritornava a Rama, perché là era la sua casa e anche là giudicava Israele. In quel luogo costruì anche un altare al Signore. » (1 Samuele 7, 17)

Persino Re Saul si allinea agli altri patriarchi:

« Saul innalzò un altare al Signore. Fu questo il primo altare che egli edificò al Signore. » (1 Samuele 14, 35)

Davide non è da meno, quando ha l'idea di fare il censimento del suo popolo; Iddio non gradisce, perchè secondo la mentalità ebraica "contare" e "misurare" significa "possedere", e solo il Signore è il padrone del suo popolo. Per questo, manda una pestilenza. L'evento storico trova così, agli occhi del credente, una giustificazione trascendente. Dietro consiglio del profeta Gad, per riparare Davide deve costruire un'ara al Signore sull'aia di Araunà il Gebuseo:

« Davide acquistò l'aia e i buoi per cinquanta sicli d'argento; edificò in quel luogo un altare al Signore e offrì olocausti e sacrifici di comunione. Il Signore si mostrò placato verso il paese e il flagello cessò di colpire il popolo. » (2Samuele 24, 24b-25)

Ovviamente Salomone erige un altare nel suo Tempio:

« La cella interna era lunga venti cubiti e alta venti. La rivestì d'oro purissimo e vi eresse un altare di cedro. » (1 Re 6, 20)

Anche il suo successore Geroboamo, primo Re del regno settentrionale, erige un altare, onde impedire che i suoi sudditi si rechino in pellegrinaggio a Gerusalemme, nel regno meridionale, erige un altare a Betel, ma vi pone un vitello d'oro, provocando un culto idolatrico che YHWH non gradirà:

« Il quindici dell'ottavo mese salì sull'altare che aveva eretto a Betel; istituì una festa per gli Israeliti e salì sull'altare per offrire incenso. » (1 Re 12, 33)

Il profeta Elia invece a un certo punto sfida i quattrocentocinquanta profeti di Baal e i quattrocento profeti di Asera, che la regina pagana Gezabele ha chiamato alla sua corte. Entrambi porranno una vittima sacrificale sopra un'ara, e il vero Dio consumerà l'olocausto (sappiamo bene come è andata a finire):

« Con le pietre Elia eresse un altare al Signore; scavò intorno un canaletto, capace di contenere due misure di seme. » (1Re 18:32)

Il Re Acaz di Giuda ricostruì l'altare del Tempio di Gerusalemme modellandolo su quello del tempio di Damasco, dopo la sconfitta del Re Rezin di Aram da parte degli Assiri:

« Il sacerdote Uria costruì l'altare, prima che il re Acaz tornasse da Damasco, facendolo proprio identico a quello che il re Acaz gli aveva mandato da Damasco. » (2 Re 16, 11)

Dopo il ritorno dall'esilio babilonese, Giosuè figlio di Iozadàk e Zorobabele figlio di Sealtiel ricostruiscono il Tempio, ed il sacerdote Esdra ne riconsacra l'altare:

« Ristabilirono l'altare al suo posto, pur angustiati dal timore delle popolazioni locali, e vi offrirono sopra olocausti al Signore, gli olocausti del mattino e della sera. » (Esdra 3:3)

E anche i Profeti nominano l'altare del Tempio nelle loro visioni:

« In quel giorno ci sarà un altare dedicato al Signore in mezzo al paese d'Egitto e una stele in onore del Signore presso la sua frontiera...» (Isaia 19, 19)
« Vidi il Signore che stava presso l'altare e mi diceva: "Percuoti il capitello e siano scossi gli architravi..." » (Amos 9, 1a)
« Offrite sul mio altare un cibo contaminato e dite: "Come ti abbiamo contaminato?" Quando voi dite: "La tavola del Signore è spregevole." (Malachia 1, 7)

Pure nel Nuovo Testamento l'altare è al centro di molti discorsi e visioni:

« Se dunque presenti la tua offerta sull'altare e lì ti ricordi che tuo fratello ha qualche cosa contro di te, lascia lì il tuo dono davanti all'altare e va' prima a riconciliarti con il tuo fratello e poi torna ad offrire il tuo dono. » (Matteo 5, 23-24)
« Quando l'Agnello aprì il quinto sigillo, vidi sotto l'altare le anime di coloro che furono immolati a causa della parola di Dio e della testimonianza che gli avevano resa... » (Apocalisse 6, 9)

L'altare a quattro corna di Tel Beersheva, oggi all'Israel
Museum of Jerusalem, VIII secolo a.C. (da questo sito)

Che cosa noi possiamo imparare, dal punto di vista matematico, da tutti questi altari? Se ne forniscono forse dei dati quantitativi? Purtroppo, solo in rari casi. Nei capitoli 25-27 dell'Esodo, pur essendo ambientati ai piedi del Monte Sinai, subito dopo che Dio ha consegnato il Decalogo a Mosè, vengono elencate tutte le istruzioni per costruire ed adornare la Tenda del Convegno, sotto il quale dimorerà l'Arca dell'Alleanza, e con esso la Shekinah, la "Presenza" di Dio, fino alla costruzione del Tempio di Salomone. A proposito dell'altare, Iddio dice:

« Farai l'altare di legno di acacia: avrà cinque cubiti di lunghezza e cinque cubiti di larghezza. L'altare sarà quadrato e avrà l'altezza di tre cubiti. Farai ai suoi quattro angoli quattro corni e saranno tutti di un pezzo. Lo rivestirai di rame. » (Esodo 27, 1-2)

Sono probabilmente parole messe in bocca al Signore dall'autore biblico, che così intende conferire maggior sacralità alla dimora terrena del Dio del Cielo. L'altare dei sacrifici, costruito secondo Esodo 38, 22-23 da Bezaleel e Ooliab della tribù di Dan,  ha dunque la forma di un parallelepipedo a base quadrata, con quattro corni alle estremità superiore, si pensa con la forma ciascuno di un ottante di sfera, per analogia con altri templi riportati alla luce dagli archeologi. Siccome un cubito biblico misurava 44,45 centimetri, le dimensioni dell'altare erano di 2,22 x 2,22 x 1,33 m, per un volume totale di 6,572 m³. Nel Primo Libro dei Re vengono date informazioni anche sulle dimensioni dell'intero Santuario del Tempio, ma sembra troppo poco per dedicare a questo argomento un intero capitolo di questo ipertesto.

Il fatto è che l'ara del Tempio ci riporta alla mente uno dei tre problemi classici della matematica greca, ed in particolare quello della duplicazione del cubo, ossia la costruzione di un cubo avente volume doppio rispetto a quello di un cubo di spigolo dato. Tale problema infatti ha un'origine religiosa, la cui prima testimonianza si fa risalire ad Eratostene da Cirene (275-195 a.C.), curatore della Biblioteca di Alessandria al tempo del re d'Egitto Tolomeo III Evergete (284-222 a.C.), come ci narra quattrocento anni più tardi il filosofo neoplatonico Teone di Smirne (70-135 d.C.). Fu quest'ultimo a coniare la definizione di "Problema di Delo". Infatti gli abitanti di Atene sarebbero stati colpiti da una pestilenza, ritenuta un castigo inviato dal dio Apollo, ed avrebbero consultato il Santuario di Delo (isola delle Cicladi famosa per essere stata sede della Lega Delio-Attica), consacrato proprio a quel dio, per chiedergli come far cessare il flagello. L'Oracolo rispose che Apollo pretendeva si duplicasse il suo altare, di forma cubica. Allora gli abitanti di Atene raddoppiarono lo spigolo dell'altare già esistente, ma la peste infuriò più di prima. Grazie al Cielo, tra gli abitanti di Atene ve ne era almeno uno appassionato di geometria, il quale fece giustamente notare che, raddoppiando i lati di un cubo, se ne ottiene un altro con volume otto volte maggiore, non di volume doppio. Duplicare il volume dell'altare significava costruirne uno nuovo, il cui spigolo si ottiene dal precedente moltiplicandolo per la radice cubica di due. Il "problema della duplicazione del cubo" consiste insomma nel costruire con riga e compasso un segmento pari alla radice cubica di due. Costruire con riga e compasso un segmento pari alla radice quadrata di due è facile, come insegnò Pitagora di Samo (570-490 a.C.): basta costruire un triangolo rettangolo isoscele i cui cateti hanno lunghezza unitaria. Per il Teorema di Pitagora, l'ipotenusa ha una misura pari alla radice di due, come spiega bene un famoso passo del dialogo "Menone" di Platone. Ben presto però ci si rese conto che la radice cubica non era altrettanto facile da ottenere.

Un altro dei classici problemi della matematica greca, quello della rettificazione della circonferenza (o della quadratura del cerchio), non è risolubile con riga e compasso, come spiegheremo in un'altra lezione, perchè il pi greco è un numero irrazionale e trascendente, cioè non può essere soluzione di alcuna equazioni algebrica a coefficienti interi. Invece la radice cubica di 2 è sì un numero irrazionale (è privo di frazione generatrice, come si può facilmente dimostrare), ma non è trascendente, essendo soluzione dell'equazione algebrica x³ – 2 = 0. Tuttavia, ai primi dell'ottocento il francese Évariste Galois (1811-1832) dimostrò con un metodo che ora non riporteremo, esulando dalle nostre finalità didattiche, che anche questa costruzione con riga e compasso è impossibile. Ciò però non significa che il problema fosse insolubile per i matematici greci, che infatti escogitarono alcune brillanti soluzioni non elementari, cioè non utilizzando solo la riga e il compasso. Di tali metodi vogliamo parlare in questa lezione.

Ippocrate di Chio (470-410 a.C.) fu il primo a rendersi conto che risolvere questo problema equivale a inserire due medi proporzionali tra 1 e 2. Infatti ciò significa scrivere:

1 : x = x : y = y : 2

e per le proprietà delle proporzioni:

y = x²   ,   2 x = y²

Sostituendo la prima nella seconda si trova:

2 x = x⁴   cioè   x³ = 2

e quindi x è pari alla radice cubica di 2! Ma anche inserire due medi proporzionali fra due numeri dati non è un quesito di immediata soluzione. Menecmo (380-320 a.C.), scopritore delle sezioni coniche, propose una geniale soluzione basata proprio su queste ultime. Infatti le due relazioni sopra scritte, y = x² e 2 x = y², se rappresentate nel piano cartesiano danno vita a due parabole, la prima con l'asse parallelo all'asse y, e la seconda con l'asse parallelo all'asse x. Inoltre la proporzione 1 : x = y : 2 può essere a sua volta riscritta nella forma x y = 2, che è a sua volta l'equazione di una iperbole equilatera con gli asintoti coincidenti con gli assi cartesiani. Rappresentando tutte e tre queste coniche nel piano cartesiano si ha:

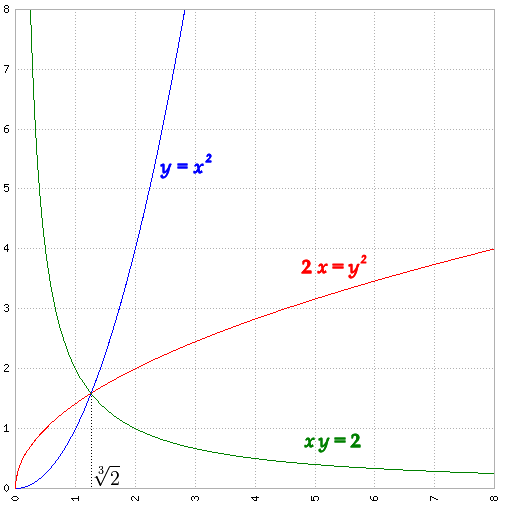
L'ascissa dell'intersezione fra le tre curve è proprio la radice cubica di 2 cercata: una soluzione davvero elegante, anche se non ci siamo pervenuti usando solo riga e compasso. Secondo alcuni, addirittura, Menecmo avrebbe introdotto tali curve proprio per risolvere questo problema!

L'altro grande matematico greco Apollonio di Perga (262–190 a.C.) propose invece la seguente costruzione. Si traccia un rettangolo ABCD di lati 1 e 2, come in figura, quindi si descrive un cerchio avente lo stesso centro Q del rettangolo e tale che due dei suoi punti d’intersezione con le rette AB e AD, indicati rispettivamente con H e K, siano allineati con C. Allora si può dimostrare che il segmento DH ha lunghezza pari alla radice cubica di 2 cercata:

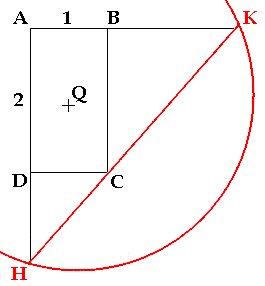
Purtroppo si tratta di una costruzione molto difficile ed approssimativa, in quanto il cerchio previsto dalla costruzione di Apollonio va cercato per tentativi, e non si può avere la certezza di aver individuato i punti giusti, come nella costruzione di un triangolo di dati lati, o di un segmento la cui lunghezza è pari alla radice di tre. Un modo per individuare con certezza i punti H e K fu proposto da Nicomede (280-210 a.C.), matematico del quale quasi nulla conosciamo al di fuori dei suoi lavori, giunti a noi grazie all'opera del matematico bizantino Proclo (412-485 d.C.), ma si tratta di una soluzione assai più complessa, che passa attraverso la definizione di una nuova curva, battezzata concoide di Nicomede.

Per costruire la concoide si segue questo procedimento. Sia data una retta r chiamata base, un punto O fuori di essa chiamato polo ed una distanza k. Tracciamo una retta passante per il punto O e un qualsiasi punto P sulla retta r. La concoide è il luogo dei punti Q₁ e Q₂ sulla retta OP, tali che i segmenti PQ1 e PQ2 siano uguali a k, al variare del punto P sulla retta r. Come si vede nel grafico sottostante, il punto Q₁ disegna un ramo della curva e il punto Q₂ un altro ramo senza punti in comune con il primo:

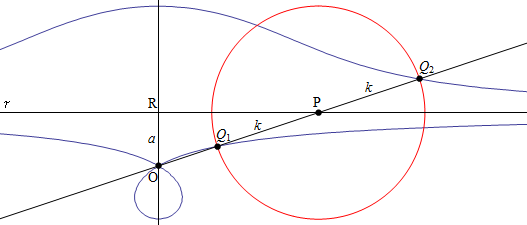
Preso come centro di un sistema di coordinate polari il polo O, come asse polare la perpendicolare ad O su r e detto R il punto di intersezione fra queste due rette, poniamo OR = a. Possiamo rappresentare la curva in coordinate polari con la seguente equazione:

Passando a coordinate cartesiane ed eseguendo alcuni facili passaggi algebrici, si ottiene l'equazione:

da cui si evince che la concoide di Nicomede è una curva del quarto ordine. Il suo nome deriva dal fatto che la sua forma ricorda quella di una conchiglia (in greco "conche"), come si evince da questo confronto:

Osserviamo che, a seconda di come si scelgono i valori di a e k, la curva ha in O un punto doppio, e precisamente un nodo se a < k, una cuspide se a = k e un punto isolato se a > k:

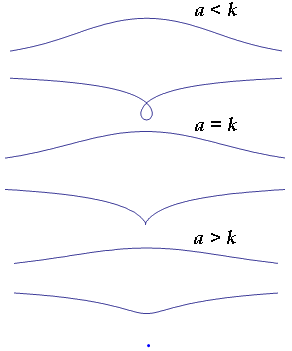
Noi però non utilizzeremo direttamente quest'equazione. Ora vi illustrerò il metodo attraverso il quale, mediante la concoide di Nicomede, si può risolve il problema delle due medie proporzionali, e quindi della duplicazione del cubo. Siano AB = 1 e AD = 2 due segmenti perpendicolari dati, tra i quali vogliamo inserire i due medi proporzionali. Si costruisce il rettangolo ABCD individuato dai segmenti dati, che è lo stesso di Apollonio visto sopra; se E è il punto medio di AD (AE = ED = 1), lo si unisce questo con C e si prolunga CE dalla parte di E fino ad incontrare in F il prolungamento di AB dalla parte di A. Chiamiamo G il punto medio di AB (AG = GB = 1/2), tracciamo la perpendicolare ad AB per G nel semipiano di bordo AB in cui non è situato il rettangolo ABCD, e con centro in B e raggio uguale ad 1 tagliamo con un arco di circonferenza questa perpendicolare nel punto L. Si unisce L con F, e da B si conduce la retta r parallela ad LF. A questo punto dobbiamo costruire la concoide avente L come polo, r come base e un parametro k = 1. Essa incontra la retta AB in un punto K, e la retta r incontra LK in un punto M con MK = 1, per definizione di concoide. La retta CK interseca la retta AD nel punto H; ebbene, i due segmenti BK e DH sono le due medie proporzionali cercate da Apollonio di Perga, e DH ha una misura pari alla radice di 2.

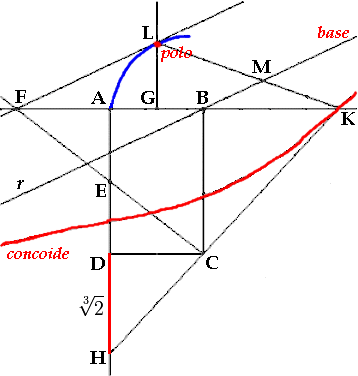
Poniamo infatti BK = x e DH = y. Si osservi che CD = DE = 1, quindi anche AE = AF = 1, perchè gli angoli CÊD e EÂF misurano 45°; di conseguenza BF = 2. FK = 2 + x. Inoltre GK = 1/2 + x, e inoltre:

Di conseguenza LK si può trovare con il Teorema di Pitagora applicato al triangolo LGK:

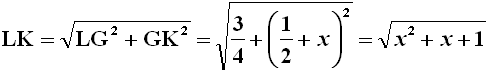
Ora, i due triangolo FLK e BMK sono simili tra di loro, essendo paralleli i due lati FL e BM, e quindi vale la proporzione:

FK : BK = LK : MK

cioè:

Da cui si ricava:

Elevando al quadrato ed eseguendo facili passaggi algebrici, si ottiene:

x⁴ + x³ – 4 x – 4 = 0

Quest'ultima equazione può essere scomposta in questo modo:

( x³ – 4 ) ( x + 1 ) = 0

Per il principio di annullamento del prodotto si ottiene o x = – 1, ovviamente non accettabile perchè x può assumere solo valori positivi, oppure x³ = 4, da cui si ricava che BK è pari alla radice cubica di 4. Ma anche i triangoli HDC e CBK sono simili tra loro per via della congruenza tra i loro angoli. Ne consegue la proporzione:

BC : DH = BK : DC

cioè:

2  :  y  =  x  :  1

e di conseguenza:

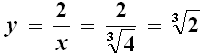
come volevasi dimostrare. Si può anche verificare, usando semplicemente il Teorema di Pitagora e un po' di algebra dei radicali, che le distanze QH e QK dei punti H e K trovati dal centro Q del rettangolo sono congruenti, e valgono precisamente:

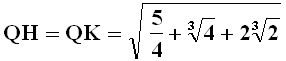
Questo vuol dire che è possibile tracciare con un compasso, facendo centro in Q e usando questa distanza come raggio, un arco di circonferenza che taglia i prolungamenti dei lati AB e AD del rettangolo in due punti allineati con il punto C; in altre parole, con questa complessa costruzione abbiamo trovato esattamente i punti H e K cercati da Apollonio di Perga! Per dirla con un celebre versetto biblico:

« Ciò che è stato sarà e ciò che si è fatto si rifarà; non c'è niente di nuovo sotto il sole. » (Qoelet 1, 9)

Tanto per confermare questo famoso detto dell'Ecclesiaste, anche Diocle di Caristo (240–180 a.C.), matematico nativo dell'isola di Eubea i cui lavori ci sono pervenuti attraverso traduzioni arabe, propose una soluzione del Problema di Delo usando un'altra curva da lui ideata, detta appunto cissoide di Diocle. Per costruire la cissoide, prendiamo una circonferenza C e la tangente l ad essa in un punto X. Detto O il punto opposto lungo il diametro al punto X di tangenza, prendiamo un punto N sulla circonferenza C e sia P il punto di intersezione della retta passante per O e N con la tangente l. Si chiama cissoide di Diocle il luogo dei punti M sulla linea OP tali che la lunghezza del segmento OM sia pari alla lunghezza del segmento NP al variare di N che si muove sulla circonferenza C, come mostra questa immagine:

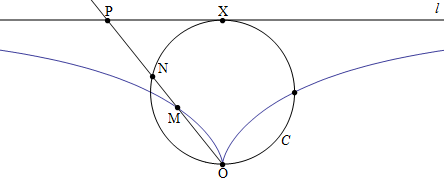
La cissoide di Diocle è simmetrica rispetto al diametro OX perpendicolare alla retta l, ed ha per asintoto la tangente alla circonferenza. Il suo nome deriva dal greco "kissos", cioè "edera", perchè l'area compresa tra la circonferenza e la cissoide internamente alla prima ha proprio la forma di una foglia d'edera, come dimostra questo confronto:

Anche in questo caso partendo dall'equazione in coordinate polari, si ricava che l'equazione cartesiana della cissoide è:

Quindi, a differenza della concoide di Nicomede, la cissoide di Diocle è una curva del terzo ordine, non del quarto, e questo ci suggerisce che potrebbe essere usata in modo semplice per trovare la sospirata radice cubica di 2. Come? Tanto per cominciare, poniamo r = 1/2, in modo che l'equazione precedente si semplifichi così:

Consideriamo un sistema di coordinate cartesiane ortogonali che ha l'origine in O, come asse x la retta OX (orientata verso X) e come asse y la retta OR (orientata verso R). Naturalmente OX = 1. Tracciamo la generica retta OS uscente dall'origine, di equazione y = m x. Essa taglia la retta l in un punto S di coordinate (1 ; m) e la cissoide nel punto T. Per trovare le coordinate di quest'ultimo, sostituiamo y = m x nell'ultima equazione cartesiana sopra scritta, e con facili passaggi algebrici otteniamo:

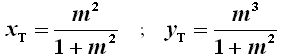
che rappresentano le equazioni parametriche della cissoide, in funzione del parametro m. Determiniamo ora l'equazione della retta TX, adoperando la formula della retta passante per due punti dati:

Sostituendovi i valori sopra trovati, si ha:

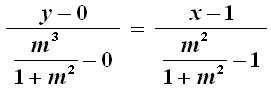
da cui si ricava:

Troviamo ora l'intersezione di questa retta con la tangente alla circonferenza condotta per O, di equazione x = 0; essa è ovviamente R ( 0 ; m³ ). Questo risultato ci permette di risolvere il problema della duplicazione del cubo, avendo costruito un segmento OR la cui lunghezza è il cubo della lunghezza di OS; o, se si preferisce, un segmento OS la cui lunghezza è la radice cubica della lunghezza di OR!

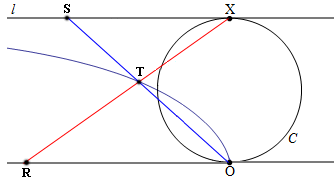
Basterà dunque eseguire la seguente costruzione. Sulla tangente in O alla circonferenza C tracciamo il segmento di lunghezza OR = 2. Congiungiamo R con X e diciamo il punto in cui RX interseca la cissoide. Congiungiamo O con T e prolunghiamo tale retta fino ad incontrare la retta l in S. Il segmento SX ha lunghezza pari alla radice cubica di 2 cercata: un metodo assai più semplice di quello che fa ricorso alla concoide!

Prima di cambiare argomento, accenniamo al fatto che alcuni in passato tentarono tutt'altra strada per risolvere il problema del cubo di volume doppio: utilizzarono infatti procedimenti meccanici.

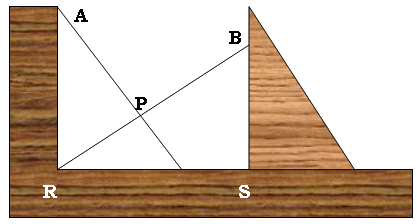
Uno di questi utilizza due squadre come quelle in figura, sfruttandole nel modo seguente. Supponiamo di voler trovare le due medie proporzionali fra a e b. Tracciamo due rette perpendicolari; detto P il punto di intersezione tra di esse, fissiamo due punti A e B, situati sulle due rette, tali che PA = a e PB = b. Posizioniamo una squadra sul disegno in modo che uno dei bracci passi per A ed il vertice R si trovi sulla retta PB. Facciamo scivolare lungo uno dei bracci della squadra un’altra squadra, nel modo indicato in figura, fino a toccare il punto B. Manipolando opportunamente l'apparato, e senza cambiare le condizioni precedenti, facciamo in modo che il punto S vada a cadere sulla retta PA. PS e PR sono allora le due medie proporzionali cercate fra PA e PQ. Se PA = 1 e PA = 2, PS rappresenta la sospirata radice cubica di 2.

Un altro metodo fu ideato dal grande Eratostene di Cirene, il quale inventò un speciale strumento da disegno, detto mesolabio, costituito da rettangoli con i lati scorrevoli, per calcolare le medie proporzionali fra due segmenti dati. Nel disegno sottostante, le lunghezze BB' e CC' sono le due medie proporzionali fra AA' e DD'.

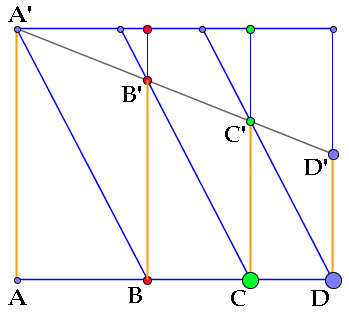
Il mesolabio di Earatostene è costituito da tre tavolette rettangolari uguali disposte fra due regoli paralleli posti su una intelaiatura, in modo tale che i regoli possano scorrere uno sull'altro: la prima tavoletta scorre sulla seconda, e questa sulla terza. I segmenti tra cui si vogliono inserire i medi proporzionali vengono riportati rispettivamente sul regolo sinistro e sul regolo destro, in modo che AA' = 2 e DD' = 1. Un filo teso mediante un peso ad un estremo congiunge i punti A' e D' e interseca i lati CC' della prima asticella e DD' della seconda rispettivamente in B' e C'. I segmenti CC' e DD' così ottenuti sono i medi proporzionali cercati, come si dimostra facilmente, e quindi nel nostro caso sono pari rispettivamente alla radice cubica di 2 e alla radice cubica di 4. Ecco invece una rappresentazione del mesolabio ideato da Cartesio, che funziona in base allo stesso principio:

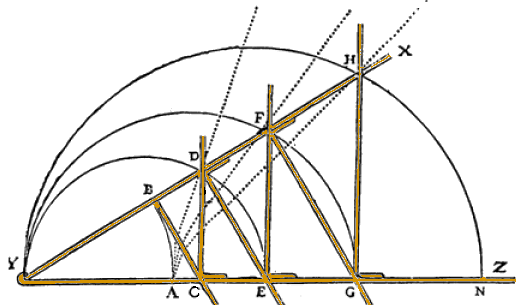
Neanche questa però si può ritenere una costruzione eseguibile con riga e compasso, dovendo ricorrere a uno strumento nuovo e così sofisticato. Certo, non si tratta di un problema semplice, ma possiamo dire di averlo risolto applicando uno dei più sensati consigli della Scrittura:

« Avete solo bisogno di costanza, perché dopo aver fatto la volontà di Dio possiate raggiungere quanto vi è stato promesso! » (Ebrei 10, 36)