Il principio del geomètra

Qual è il geometra che tutto s'affige
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige...

(Par. XXXIII, 133-135)

La parola "geometria" in greco significa "misura della terra". Gli antichi Greci le diedero questo nome perché ad idearla erano stati gli antichi Egizi: ogni volta che il Nilo inondava i campi, si rendeva necessario misurare di nuovo gli appezzamenti di terra onde ripristinare i confini di proprietà. Non a caso uno dei testi più antichi che trattano di questa scienza è il cosiddetto Papiro di Rhind, compilato verso il 1650 a.C. dallo scriba Ahmes al tempo dell'occupazione Hyksos dell'Egitto, ma ritenuto la copia di un originale più antico risalente circa al 2000 a.C.. Ma oggi sappiamo che, contemporaneamente agli Egizi, anche i popoli mesopotamici avevano avanzate conoscenze di geometria, legate soprattutto a problemi di astronomia e di architettura. Comunque tanto gli Assiro-Babilonesi quanto gli Egiziani studiavano la geometria per fini essenzialmente pratici. Furono proprio i Greci a trasformare la geometria in una scienza astratta, che studia figure ideali come quadrati e cerchi perfetti, e non appezzamenti di terra di forma quadrata o circolare. I primi grandi nomi di questa a partire da Talete di Mileto (624-547 a.C.), uno dei sette savi dell'antica Grecia, definito da Apuleio « il primo scopritore della geometria », e Pitagora di Samo (575-495 a.C.), fondatore dell'omonima scuola a Crotone, cui si attribuisce la prima dimostrazione di quello che oggi infatti è noto come Teorema di Pitagora, empiricamente già noto in Egitto e in Mesopotamia. Platone (428-348 a.C.) pose la geometria come fondamento degli studi filosofici, tanto da far scrivere sulla porta della sua scuola: « Nessuno ignaro della geometria entri qui ».

Il vero "inventore" della geometria come oggi la conosciamo è però Euclide di Alessandria (367-283 a.C.), il quale nei suoi "Elementi", testo fondamentale per lo studio della geometria durante tutta l'età classica ed il Medioevo, e quindi anche per Dante, mostrò come tutti i teoremi e le proprietà delle figure piane e solide potessero essere ricavate induttivamente da pochi postulati stabiliti a priori. Da allora, tutte le scienze tentarono di basarsi su di una struttura logica analoga: pochi assiomi e una serie di definizioni, dalle quali derivare per pura logica tutte le verità scientificamente dimostrabili, e decretare assurde tutte le altre. L'Alighieri riconosce la sua posizione di rilievo nella cultura medioevale incontrandolo nel Limbo insieme agli « spiriti magni » e associandolo a un altro grande scienziato dell'antichità, Tolomeo, del quale riparleremo a proposito dell'astronomia dantesca:

Euclide ritratto nella "Scuola d'Atene" di Raffaello con le sembianze
di Donato Bramante (Vaticano, Stanza della Segnatura, 1508-1511)

Ma il più grande esperto di matematica e di geometria del mondo antico fu certamente Archimede di Siracusa (287-212 a.C.) che, oltre ad essere un grande fisico ed ingegnere, affrontò per primo problemi considerati ai suoi tempi insolubili come il calcolo delle aree e dei volumi della sfera e di parte della sfera, e gettò addirittura le basi del calcolo infinitesimale. Le sue geniali idee non furono però pienamente comprese dai suoi contemporanei. Bisogna inoltre ricordare Ippocrate di Chio (470-410 a.C.) e Archita di Taranto (428-347 a.C.), che risolsero il famoso problema della duplicazione del cubo, e Apollonio di Perga (262-190 a.C.), che ideò le sezioni coniche (ellisse, iperbole, parabola). Gli ultimi grandi geometri greci dell'antichità furono Pappo di Alessandria (IV sec. d.C.), anticipatore della geometria proiettiva ed autore delle "Collezioni matematiche", una preziosa documentazione storica concernente alcuni aspetti della matematica greca che altrimenti ci sarebbero rimasti sconosciuti; e Ipazia (370-415), una delle ultime figure del paganesimo classico, rimasta vittima degli scontri politici e religiosi che accompagnarono l'agonia dell'Impero Romano.

Tra i Romani si occuparono di geometria Vitruvio (I sec. a.C), Plinio il Vecchio (23-79 d.C.) e Severino Boezio (475-525), che non compirono grandi passi in avanti, ma ad ogni modo la geometria, come parte integrante della Matematica, entrò a far parte delle Arti del Quadrivio, studiate da tutti i dotti del Medioevo. La geometria fiorì invece in India, grazie all'opera di grandi intelletti come Brahmagupta (598–668) ed Aryabhata (476-550), quest'ultimo detto "l'Euclide indiano". Con le scoperte indiane vennero a contatto gli Arabi, i quali riscopersero e tradussero le opere di Euclide e degli altri matematici greci. Tra i molti grandi esperti di geometria dell'Oriente musulmano ricordiamo l'iracheno Muhammad ibn Jabir al-Battani (858–929), ideatore della trigonometria; l'iracheno Abu Hasan Thabit ibn Qurra' ibn Marwan al-Sabi' al-Harrani (826-901) che anticipò le geometrie non euclidee; il persiano Sharaf al-Din al-Muzaffar al-Tusi (1135-1213), che pose le basi dello studio delle curve tramite equazioni, fondando la geometria algebrica; ed il persiano Ghiyath al-Din Jamshid Mas'ud al-Kashi (1380-1429) che, come vedremo, si occupò del calcolo delle cifre esatte di π.

Siccome in Spagna cristiani e musulmani si confrontarono a lungo, combattendosi ma spesso anche rispettando le reciproche culture, le conoscenze dei greci vennero riscoperte dall'occidente cristiano, dove Euclide era rimasto un pilastro fondante della cultura scientifica. Al ritorno di fiamma degli studi di geometria contribuì non poco anche la scoperta della prospettiva, che in base a quanto ci è rimasto sfuggì probabilmente ai Greci e ai Romani, e non interessò affatto né ai Bizantini né all'Occidente nell'alto Medioevo, quando il fine delle arti figurative era evocare il trascendente, tralasciando volutamente un oggettivo realismo nelle rappresentazioni. Il primo a cercare una rappresentazione plastica e realistica della realtà fu Giotto di Bondone (1267-1337), contemporaneo di Dante, da questi citato nel Purgatorio:

« Credette Cimabue ne la pittura
tener lo campo, e ora ha Giotto il grido,
sì che la fama di colui è scura » (Purg. XI, 94-96)

Era perciò inevitabile che si sviluppasse la ricerca geometrica di procedimenti pittorici destinati ad ottenere una maggiore corrispondenza alla percezione visiva dell'occhio umano. Uno dei primi dipinti che mostrano un uso consapevole delle regole geometriche della prospettiva è l'"Annunciazione" di Ambrogio Lorenzetti (1298-1348), una tempera su tavola dipinta nel 1344, quindi poco dopo la scomparsa dell'Alighieri. Un importante salto di qualità lo si ebbe grazie all'opera del grande architetto fiorentino Filippo Brunelleschi (1377-1446), il quale, attraverso esperienze condotte con l'aiuto di strumenti ottici, elaborò per primo un procedimento corretto per rappresentare gli edifici in prospettiva, poi descritto dall'umanista Leon Battista Alberti (1404-1472) nella prima trattazione scritta di questo argomento, il "De Pictura" (1434-1436). Tra i grandi pittori di quest'epoca che applicarono nelle loro opere le teorie di Brunelleschi e dell'Alberti si annoverano Masaccio (1401-1428), Melozzo da Forlì (1438-1494) e Piero della Francesca (1416-1492), quest'ultimo anche autore del trattato in volgare "De perspectiva pingendi"., oltre ovviamente a Leonardo da Vinci (1452-1519).

Nel Rinascimento italiano, che pure fu ricchissimo di grandi esperti di Matematica, vanno ricordati il messinese Francesco Maurolico (1494-1575), a cui dobbiamo l'anticipazione della geometria differenziale, e il milanese Bonaventura Cavalieri (1598-1647), amico di Galileo, ideatore del "metodo degli indivisibili" per determinare aree e volumi, una tappa fondamentale verso l'elaborazione del calcolo infinitesimale. I francesi Renato Cartesio (1596-1650) e Pierre de Fermat (1601-1665) fondarono la geometria analitica; in particolare Fermat, un mero dilettante divenuto uno dei più grandi matematici di ogni tempo, introdusse l'"isomorfismo" fra struttura algebrica e geometria, cioè la traduzione esatta del linguaggio della geometria in quello dell'algebra e viceversa. Lo scozzese James Gregory (1638-1675) proseguì gli studi di Cavalieri e Fermat nel suo trattato "Geometriae pars universalis" (1667), sistematizzando il concetto di integrale. Il Settecento fu il secolo di Leonardo Eulero (1707-1783), che portò fondamentali contributi a molti rami della matematica, compresa la geometria. Nel secondo volume della sua "Introductio in analysin infinitorum" (1748) egli estese la geometria analitica di Cartesio e Fermat allo spazio tridimensionale; introdusse le coordinate polari; scoprì che il raggio R della circonferenza circoscritta a un triangolo di lati a, b, c ed area S è pari a R = abc/4S; ideò la Relazione di Eulero (il numero dei vertici di un poliedro più il numero delle sue facce è pari al numero degli spigoli aumentato di 2); e, risolvendo nel 1736 il celebre problema dei sette ponti di Königsberg, avviò lo studio della Geometria di Posizione, oggi nota come topologia.

Il bergamasco Lorenzo Mascheroni (1750-1800) con la sua "Geometria del compasso" (1797), nella quale dimostrò che tutte le costruzioni geometriche effettuabili con riga e compasso possono venire fatte usando solamente il secondo strumento. Adrien Marie Legendre (1752-1833) apportò un valido contributo a questa scienza con i suoi "Elements de geometrie" (1794), mentre Lazare Carnot (1753-1823) proseguì lo studio della topologia e Gaspard Monge (1746-1818) con i "Feuilles d'analyse" (1795) fondò la geometria differenziale. Carl Friedrich Gauss (1777-1855), detto "il Principe dei Matematici", fu l'ultimo matematico universale, capace cioè di occuparsi di ogni branca di questa disciplina; nel campo della geometria dimostrò tra l'altro il teorema secondo cui una circonferenza si può dividere con riga e compasso in un numero n di parti uguali, soltanto se n, scomposto in fattori primi, ha i fattori diversi da 2 tutti alla prima potenza e tali che diminuiti di 1 diano luogo ad una potenza di 2. In base a questo teorema non è possibile dividere con riga e compasso una circonferenza in 7, 11 e 13 parti uguali, perché tali numeri primi diminuiti di 1 non danno una potenza di 2, né in 9 parti uguali, perché 9 = 3² e il fattore 3 non si presenta alla prima potenza; al contrario, mediante riga e compasso è possibile dividere la circonferenza in 17 parti uguali, poiché 17 - 1 = 2⁴ (la suddivisione della circonferenza in 17 parti uguali era sfuggita completamente agli antichi, ed è frutto delle ricerche di Gauss).

A partire dal 1829 con Nikolai Ivanovic Lobacevskij (1772-1865) sviluppò la prima geometria non euclidea, detta geometria iperbolica, e nel 1854 Bernhard Riemann (1826-1866) ne costruì un'altra, stavolta detta geometria ellittica; di queste riparleremo più avanti. Lo stesso Riemann, quando nel 1854 diventò Privatdozent all'Università di Göttingen, uno dei centri propulsivi della moderna ricerca matematica, pronunciò la più famosa dissertazione di abilitazione della storia della matematica, intitolata "Über die Hypothesen welche der Geometrie zugrunde liegen" ("Sulle ipotesi che stanno alla base della geometria"), che rifonda completamente le basi di questa scienza, trasformandola nello studio di varietà di un numero qualsiasi di dimensioni in qualsiasi genere di spazio. Da allora non si parla più di geometria, ma di "geometrie" di Riemann. Felix Klein (1849-1925) dal canto suo dimostrò la coerenza logica delle geometrie non euclidee, provando che rappresentano casi particolari di una geometria più generale, quella proiettiva. Egli inoltre avviò il cosiddetto Programma di Erlangen (1872), nel quale mostrò come le proprietà essenziali di una data geometria possono essere rappresentate dal gruppo delle trasformazioni che conservano tali proprietà. Nel 1899 David Hilbert (1862-1943) pubblicò il saggio "Grundlagen der Geometrie" ("Fondamenti della geometria"), nel quale dava alla geometria un assetto puramente formale e assiomatico, basato su ventuno assiomi e svincolato da ogni rappresentazione "grafica". Nel solco di Hilbert si mosse il piemontese Giuseppe Peano (1858-1932), matematico eccentrico e geniale, che fornì il primo esempio di una curva tale da riempire completamente un'area, mettendo così in evidenza come la definizione di curva allora vigente non fosse conforme a quanto intuitivamente si intende con questo termine: oggi sappiamo che la "Curva di Peano" rappresenta uno dei primi esempi storicamente noti di frattale. Nel 1904 Henri Poincaré (1854-1912) fondò quella che poi sarebbe stata chiamata geometria algebrica, concentrandosi in particolare sulle proprietà topologiche della cosiddetta tre-sfera (ne riparleremo più avanti in questo ipertesto), e formulò la cosiddetta Congettura di Poincaré, la cui dimostrazione appassionò i matematici per cent'anni, e venne portata a termine solo nel 2003 dal russo Grigorij Jakovlevic Perel'man (1966-). A portare avanti questo filone della Matematica, che si occupa di oggetti geometrici definiti come zeri di un certo numero di polinomi, fu la grande scuola italiana di geometria algebrica, i cui maggiori cultori furono Corrado Segre (1863-1924), Guido Castelnuovo (1865-1952), Federigo Enriques (1871-1946), Francesco Severi (1879-1961) e Oscar Chisini (1889-1967), quest'ultimo fondatore dell'Istituto di Matematica presso l'Università degli studi di Milano, e docente della madre dell'autore di questo sito.

Il logo del Politecnico di Milano, alma mater studiorum
dell'autore di questo sito, riproduce l'Euclide di Raffaello!

Intanto, l'invenzione dei calcolatori elettronici permetteva di risolvere due importanti problemi rimasti a lungo senza soluzione: il Teorema dei Quattro Colori, secondo il quale ogni mappa più essere colorata senza che due regioni abbiano lo stesso colore usando soltanto quattro colori, dimostrato nel 1976 da Kenneth Appel (1932-) e Wolfgang Haken (1928-); e la Congettura di Keplero, secondo cui non esiste alcun modo di sistemare delle sfere nello spazio con densità media superiore a quella dell'impacchettamento cubico a facce centrate o a quella dell'impacchettamento esagonale, risolta nel 1998 da Thomas Hales (1958-). Intanto nella geometria facevano irruzione i frattali, figure dotate di area finita e perimetro infinito, caratterizzate dalla strana circostanza di avere un numero frazionario di dimensione intera. I pionieri di questo studio furono il francese Gaston Maurice Julia (1893-1978) e lo svedese Helge von Koch (1870-1924), ma a portarlo al suo massimo splendore fu il polacco Benoit Mandelbrot (1924-2010) negli anni '80 del secolo scorso. L'analisi frattale delle variabili economiche e finanziarie ha portato negli anni 2000 ad importanti applicazioni nel campo dell'economia.

Torniamo ora alle origini. Grazie soprattutto all'opera di Euclide, la geometria ha rappresentato un modello di sapere perfettamente strutturato, che discende da determinati assiomi e porta alla dimostrazione incontrovertibile della verità di certe affermazioni e della falsità di altre. Questo modo di ragionare indubbiamente affascinò anche il nostro poeta che, non dimentichiamolo, quanto dovette iscriversi ad una delle Corporazioni Maggiori di Firenze, scelse quella degli Speziali, e dunque era tutt'altro che digiuno di scienza. La prova la troviamo ad esempio nel fatto che, per descrivere ai lettori la Visione di Dio da lui avuta nel Canto XXVIII del Paradiso, egli decide di far ricorso al concetto tutto euclideo di punto geometrico:

« Un punto vidi che raggiava lume
acuto sì, che 'l viso ch'elli affoca
chiuder conviensi per lo forte acume;
e quale stella par quinci più poca,
parrebbe luna, locata con esso
come stella con stella si collòca. (Par. XXVIII, 16-21)

Quel punto emette una luce tanto intensa, che l'occhio da esso scottato è costretto a chiudersi per l'insostenibile luminosità da esso irraggiata; eppure, a Dante appare così piccolo che qualsiasi stella appaia minuscola ("poca") ai nostri occhi, sembrerebbe grande come la luna piena, se fosse posta vicina ad essa. Il punto euclideo è privo di dimensioni, quindi indivisibile e immateriale, e dunque secondo Dante è il simbolo più appropriato di Dio, sulla scorta di un passo di San Tommaso:

« Ens omnino simplex, maxime Ens et maxime Indivisum »
[Ente assolutamente semplice... sommamente Ente e sommamente Indivisibile] (Summa Theologica I, III, 7 e I, XI, 3)

Ma l'Alighieri non limita certo le proprie conoscenze di geometria all'utilizzo di un mero concetto in senso allegorico. Tanto per cominciare, egli sa utilizzare gli strumenti propri della geometria, come ad esempio il compasso. Infatti nel Canto XIX del Paradiso l'Aquila formata dai Beati nel Cielo di Giove usa questa circonlocuzione per riferirsi a Dio:

« ...Colui che volse il sesto
a lo stremo del mondo, e dentro ad esso
distinse tanto occulto e manifesto... » (Par. XIX, 40-42)

Quel "sesto" è proprio il compasso, tanto caro a disegnatori e studenti di geometria, perché poteva essere aperto fino ad un sesto di cerchio, cioè fino a 60°. Si noti che, attraverso quest'immagine, il Signore è rappresentato proprio come un geometra, che traccia i confini ("lo stremo") del mondo esattamente come un architetto fa con l'edificio che deve costruire, ordinandovi tutte le cose occulte e tutte le cose manifeste, sulla scorta di almeno due evocativi passaggi biblici:

« Quando Egli fissava i cieli, io ero là, quando tracciava un cerchio sull'abisso » (Prov 8, 27)

« Dov'eri tu quand'io ponevo le fondamenta della terra? Dillo, se hai tanta intelligenza! Chi ha fissato le sue dimensioni, se lo sai, o chi ha teso su di essa il regolo? Dove sono fissate le sue basi, chi ha posto la sua pietra angolare, mentre gioivano in coro le stelle del mattino e plaudivano tutti i figli di Dio? » (Giobbe 38, 4-7)

Spostiamoci ora in uno dei canti emotivamente più intensi della Divina Commedia, il XVII del Paradiso, che come noto è interamente concentrato sull'incontro tra Dante e il suo trisavolo Cacciaguida: in esso gli annuncia l'esilio e lo legittima in quanto poeta investito di una missione universale nei confronti di tutti i suoi compatrioti. Le parole che i due si scambiano sono tra le più complesse e ricche di immagini della Commedia, e non è certo un caso se alcune di queste immagini sono tolte proprio dalla Geometria Euclidea:

« O cara piota mia, che sì t'insusi,
che come veggion le terrene menti
non capere in triangol due ottusi,
così vedi le cose contingenti
anzi che sieno in sé, mirando il punto
a cui tutti li tempi son presenti » (Par. XVII, 13-18)

"Piota" è la pianta del piede in dialetto fiorentino, e quindi è una metafora per indicare "la mia radice", cioè "il mio antenato". Questa "piota", cioè Cacciaguida, è apostrofata come colui che "si insusa", cioè si innalza, al punto da conoscere gli eventi prima ancora che si avverino, leggendoli in Dio, "Colui a cui tutti i tempi sono presenti", perchè vive fuori dal tempo e tutti i secoli abbraccia con il suo sguardo. Come dice infatti San Tommaso d'Aquino:

« Praecognoscere futura est proprium Divini Intellectus, cuius aeternitati sunt omnia praesentia »
[Conoscere in anticipo gli eventi futuri è tipico dell'Intelletto Divino, alla cui eternità tutte le cose sono presenti]
(Summa Theologica II, CLXXII, 1)

Del fatto che Cacciaguida possiede una capacità di chiaroveggenza, Dante è ultrasicuro; ne è sicuro quanto... quale immagine usare per dare l'idea di una tale certezza incrollabile? Niente di meglio che far ricorso alla Geometria. Il Ghibellin Fuggiasco ne è certo quanto del fatto che in un triangolo non possono sussistere due angoli ottusi! Infatti una delle formulazioni del famoso Quinto Postulato di Euclide è la seguente:

Nella formulazione moderna questo postulato suona così (è il cosiddetto enunciato di Playfair):

« Per un punto fuori di una retta passa una e una sola retta parallela alla retta data »

Da questa è facile risalire alla formulazione che chiama in causa il triangolo. Si consideri infatti la figura soprastante. Dato il triangolo ABC, per C si conduca l'unica parallela ad AB permessa dal Quinto Postulato. Gli angoli BAC ed ACD (in viola) sono tra loro congruenti perchè angoli alterni interni delle rette parallele AB e CD tagliate dalla trasversale AC, come pure gli angoli ABC e BCE (in azzurro) sono alterni interni delle rette parallele AB e CE tagliate dalla trasversale BC. Ne consegue che:

Se dunque la parallela tracciata da un punto esterno ad una retta è unica, allora la somma degli angoli interni di un triangolo è pari ad un angolo piatto. Infatti, nelle geometrie non euclidee in cui il Quinto Postulato non vale, la somma degli angoli interni di un triangolo è maggiore (geometrie ellittiche) o minore (geometrie iperboliche) di 180°. Siccome due angoli ottusi sono entrambi maggiori di 90°, la loro somma sarà maggiore di 180°, e quindi in un triangolo due ottusi non potranno mai « capere », cioè essere contenuti, due angoli ottusi. E questo è stato ricavato dai Postulati iniziali mediante un ragionamento che non può essere messo in discussione da nessuno (vedi "Elementi", Libro I, teorema XVII).

È una delle più unanimemente accettate qualità della matematica quella cui il nostro autore si appiglia in questi versi: l'insindacabile certezza dei suoi teoremi, che per Dante assurge a simbolo del massimo livello di verità che la mente umana può concepire. Con la stessa sicurezza con cui l'uomo è in grado di dimostrare che in un triangolo non possono convivere due angoli ottusi, altrettanto Dante è certo che il beato Cacciaguida è in grado di vedere passato, presente e futuro. Anzi, l'immagine che Dante Alighieri ci comunica è ancora più raffinata: nella fantasia del lettore si affiancano infatti due figure di segno opposto. Da un lato il triangolo che nella finitudine dell'angolo piatto non può contenere i due eccessivamente aperti angoli ottusi; dall'altro il simbolo per eccellenza della finitudine, il punto, che invece riesce ad accogliere in sé l'infinito e l'eternità. È lo scacco della ragione umana, l'abisso incolmabile tra finito e infinito, che Dante riesce ad esprimere proprio usando la scienza che ai suoi tempi in massimo grado rappresentava il trionfo delle capacità logico-deduttive umane, la Geometria.

Detto per inciso, il discorso sul Quinto Postulato di Euclide ci potrebbe portare diritti a trattare l'argomento delle geometrie non euclidee, perchè incredibilmente Dante fece uso anche di esse, con un anticipo di cinque secoli su mostri sacri della matematica come Gauss e Riemann; ma preferisco rimandare questo discorso alla lezione dedicata all'Astrofisica, se avrete la pazienza di seguirmi fino a quel punto!

Come a sottolineare l'incontrovertibilità dei teoremi della Geometria come simbolo dell'incontrovertibile vittoria dell'Onnipotenza Divina nei Cieli del Paradiso, pochi versi più avanti Dante aggiunge:

« dette mi fuor di mia vita futura
parole gravi, avvegna ch'io mi senta
ben tetragono ai colpi di ventura » (Par. XVII, 23-24)

La certezza che infonde la scienza non è solo desunta dall'infallibilità dei suoi ragionamenti, ma a un livello più intuitivo sono le sue forme stesse a suggerirlo. E chi non vorrebbe affrontare gli sferzanti colpi del destino con la sicura stabilità di un rettangolo? Infatti il tetragono è, come dice l'etimologia greca, ogni figura geometrica con quattro angoli, proprio come una fortezza medioevale di forma rettangolare. Per estensione, la mente corre al parallelepipedo che poggia ugualmente bene su ognuna delle sei facce, proprio come il virtuoso può resistere in qualunque situazione di fortuna.

In modo analogo un concetto matematico assai noto era già stato utilizzato da Dante quattro canti prima:

« Non ho parlato sì, che tu non posse
ben veder ch'el fu re, che chiese senno
acciò che re sufficïente fosse;
non per sapere il numero in che enno
li motor di qua sù, o se necesse
con contingente mai necesse fenno;
non si est dare primum motum esse,
o se del mezzo cerchio far si puote
trïangol sì ch'un retto non avesse » (Par. XIII, 94-102)

Il testo sembra un po' difficile, in accordo con il tono alto e concettoso di tutto il Paradiso, ma in pratica il suo significato è il seguente. A parlare è San Tommaso d'Aquino, il quale intende sciogliere un dubbio di Dante già enunciato nel canto XI e rimasto fin qui insoluto, giacché, parlando di Salomone, l'Aquinate aveva affermato:

« entro v'è l'alta mente u' sì profondo
saver fu messo, che, se 'l vero è vero,
a veder tanto non surse il secondo » (Par. X, 112-114)

Non è da ritenere che la perfezione della Sapienza umana sia stata assegnata prima ad Adamo e poi a Gesù in quanto uomo, e che pertanto sia da ritenere erronea la tradizionale opinione che considera re Salomone il più sapiente tra gli uomini? La risposta di San Tommaso si sviluppa ampiamente, come si conviene al massimo teologo della Scolastica, e la prende alla larga, cominciando con la dimostrazione della verità della perfetta sapienza di Adamo e dell'Uomo-Dio: solo gli esseri creati direttamente da Dio sono perfetti, dotati della maggior perfezione possibile in una creatura, e tali furono appunto Adamo nel Paradiso Terrestre, e il Verbo incarnato e fatto uomo. Successivamente Tommaso dimostra la verità dell'eccellenza del sapere di Salomone, affermando che essa non si riferisce ad argomenti metafisici o dialettici, ma solo alla prudenza del governo, in quanto il figlio di Davide fu il più sapiente dei Re della Terra. Non ho parlato così oscuramente, dice Tommaso a Dante, che tu non possa comprendere che io mi riferivo a Salomone in quanto re, ed egli chiese a Dio la Sapienza solo per poter espletare questo alto ufficio, pur essendo giovane e inesperto. I versi 97-102 del Canto XIII, da noi riportati sopra, enunciano una serie di problemi filosofici e scientifici attinenti a quel tipo di sapienza che Salomone non chiese e non ottenne dal Signore, essendo superflua al compito che gli era stato assegnato. I problemi enunciati sono, nell'ordine:

1) quante siano le Intelligenze Motrici, problema che Dante affronta nel Convivio (II, IV, 3-15) e in Paradiso XXVIII, 92-93 (i versi di cui abbiamo già parlato a proposito del "doppiar degli scacchi");

2) se da una premessa necessaria e da una contingente si possa dedurre una conclusione necessaria: questione schiettamente filosofica, confutata da Aristotele negli "Analitici Primi" (I, 16), come abbiamo già accennato in un altro capitolo;

3) se si deve ammettere nell'universo un primo moto che non sia effetto di un altro moto, e dal quale tutti dipendono (« si est dare primum motum esse »). La risposta la fornisce lo stesso Tommaso nella sua opera:

« Omne quod movetur, oportet ab alio moveri... Hic autem non est procedere in infinitum; quia sic non esset aliquod primum movens... Ergo necesse est devenire ad aliquod primum movens, quod a nullo movetur: et hoc omnes intelligunt Deum »
[Tutto ciò che si muove, è necessario che sia mosso da altro... Non si può qui procedere all'infinito... è necessario dunque pervenire a un primo motore, che non è mosso da nessuno: e questo tutti lo chiamiamo Dio] (Summa Theologica I, II, 3)

4) e finalmente, se in un semicerchio possa essere inscritto un triangolo che non sia rettangolo. Questa questione è prettamente geometrica, come quella dei due angoli ottusi in un triangolo, ed infatti è dimostrabile secondo gli insegnamenti di Euclide.

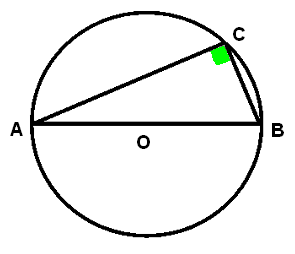
Con facili passaggi è possibile dimostrare che ogni angolo alla circonferenza è pari alla metà dell'angolo al centro che insiste sullo stesso angolo. Se costruiamo un triangolo ABC inscritto in una semicirconferenza, come si vede nella figura soprastante, l'angolo alla circonferenza ACB sarà pari alla metà dell'angolo al centro AOB, che è piatto; dunque ACB = 90°. La risposta alla quarta questione è perciò negativa: nessun triangolo che non sia rettangolo può essere inscritto nel « mezzo cerchio ».

Quattro sono dunque le forme più alte di Sapienza che Tommaso riconosce, distinte da quella necessaria per governare. Si tratta della Teologia, della Dialettica, della Filosofia e, appunto della Geometria. E questo, in un'epoca - il Medioevo - che i più tacciano pregiudizialmente di essere "oscura" ed assolutamente refrattaria ad ogni ricerca di tipo scientifico!

Tuttavia il più famoso riferimento alla Geometria contenuto nella Divina Commedia è molto probabilmente quello che si trova solo pochi versi prima della fine del « sacrato poema », e riguarda uno dei problemi più dibattuti nella storia della Matematica: quello dell'esatta misura della circonferenza.

La questione di misurare con esattezza il rapporto tra circonferenza e diametro, da noi universalmente indicato con il simbolo π (pi greco), risale alle origini della geometria, e ha tenuto occupati i matematici per secoli. La più antica documentazione esistente di questo problema risale al già citato Papiro di Rhind, nel quale troviamo scritto:

« Togli 1/9 a un diametro e costruisci un quadrato sulla parte che ne rimane; questo quadrato ha la stessa area del cerchio. »

Poiché sappiamo che l'area del cerchio è uguale al raggio al quadrato per pi greco, se quest'area è il quadrato di 8/9 del diametro, la costruzione di Ahmes implica che il rapporto tra circonferenza e diametro sia pari a 16/9 = 3,16049… Questo valore si discostava di meno dell'1 % dal vero valore di circa 3,141592..., dimostrando che gli antichi egizi possedevano notevoli conoscenze di geometria fin dalla più remota antichità.

Invece Babilonesi ed Ebrei furono molto meno bravi nell'approssimare questo rapporto. Nella Bibbia (VI secolo a.C.) leggiamo infatti, a proposito della costruzione del Tempio di Salomone:

« Fece un bacino di metallo fuso di dieci cubiti da un orlo all'altro, rotondo; la sua altezza era di cinque cubiti e la sua circonferenza di trenta cubiti » (1 Re 7, 23)

Evidentemente dunque il rapporto tra circonferenza e cerchio era ritenuto pari a 3, un risultato certamente molto meno esatto di quello egiziano. Il primo pensatore greco a cercare di trovare un rapporto definitivo fra un cerchio e un quadrato fu Anassagora di Clazomene (496-428 a.C.), autore del primo tentativo di quadratura del cerchio con riga e compasso. Archimede di Siracusa (287-212 a.C.) nella sua opera "Misura del cerchio" confrontò una serie di poligoni regolari inscritti e circoscritti: partendo dall'esagono e raddoppiando progressivamente il numero dei lati, si spinse fino a poligoni di 96 è provò che:

Il romano Vitruvio (I sec. a.C) usò invece il rapporto 25/8, mentre Tolomeo (II sec. d.C.) utilizzò 377/120 = 3,14166... I cinesi Chang Hong e Wang Fau nel III secolo d.C. usarono indipendentemente lo stesso metodo di Archimede spingendosi fino al poligono di 192 lati, e trovarono π = 142/45. Il matematico indiano Aryabhata (V sec. d.C.) sfruttò invece la frazione 62832/20000. Nel 1220 Leonardo Fibonacci (1170-1240), uno dei massimi matematici del Medioevo, trovò con il metodo di Archimede il valore 3,141818, mentre l'arabo al Kashi (1380-1429) calcolò le prime 14 cifre esatte di π.

Il vicario William Oughtred (1575-1660) fu il primo ad usare la lettera pi greca per indicare il rapporto costante tra circonferenza e diametro; secondo alcuni lo usò essendo la prima lettera di περίμετρος (perimetro), mentre secondo altri si tratta dell'iniziale del nome di Pitagora. L'uso di questo simbolo tuttavia si diffuse solo a partire da quando lo usò Eulero nel 1734.

Il numero è chiamato anche Numero di Ludolph, poichè Ludolph van Ceulen (1540-1619) fu il primo a noi noto a calcolarlo con 35 cifre decimali esatte: era così fiero del suo risultato che lo fece incidere sulla sua lapide. Nel 1654 Christiaan Huygens (1629-1703) perfezionò il metodo di Archimede e trovò che:

Nel 1665 Isaac Newton (1642-1727) introdusse il calcolo infinitesimale e calcolò π fino alla sedicesima cifra decimale. Nel 1674 Gottfried Wilhelm von Leibnitz (1646-1716) scoprì che π si può ottenere come somma di una serie a termini razionali:

Nel 1699 Abraham Sharp (1653-1742) giunse a 72 cifre, e nel 1719 Thomas Fantet de Lagny (1660-1734) calcolò 127 cifre, di cui 112 esatte. Nel 1735 lo svizzero Leonardo Eulero (1707-1783) trovò un'altra serie a termini razionali:

Solo nel 1761 Johann Heinrich Lambert (1728-1777) dimostrò che π è un numero irrazionale, e dunque è privo di frazione generatrice: circonferenza e diametro sono dunque grandezze incommensurabili. Eulero ipotizzò che π fosse anche trascendente, cioè che non potesse essere soluzione di alcuna equazione a coefficienti interi.

Il matematico sloveno Jurij Vega (1754-1802) nel 1789 calcolò le prime 140 cifre decimali di π, di cui le prime 137 erano corrette, e nel 1841 William Rutherford (1798–1871) calcolò 208 cifre decimali di cui 152 corrette. Nel 1874 William Shanks (1812-1882) dopo anni di lavoro ottenne 707 cifre, ma solo 527 erano corrette.

La dimostrazione definitiva della trascendenza di pi greco la si deve al tedesco Ferdinand von Lindemann (1852-1939) nel 1882. Ciò esclude che sia possibile rettificare la circonferenza e quadrare il cerchio con il solo uso di riga e compasso, come speravano tutti i matematici da Archimede fino alla soglia dell'età moderna. Questo problema è bensì risolubile attraverso curve particolari come la quadratrice.

Il XX secolo vide l'introduzione degli strumenti di calcolo elettronico. Nel 1947 D. F. Ferguson calcolò 808 cifre in circa un anno, utilizzando una delle prime calcolatrici da tavolo, mentre nel 1948 George Rietwiesner, John von Neumann e Nicholas Constantine Metropolis arrivarono a 2.037 cifre, calcolate in 70 ore utilizzando l'ENIAC, il primo grande calcolatore elettronico della storia. Nel 1961 John Wrench e Daniel Shanks raggiunsero le 100.265 cifre in 8 ore e 43 minuti, usando un IBM 7090. Era il 1973 quando Jean Guilloud e M. Bouyer sfondarono il muro del milione di cifre calcolate in 23 ore e 18 minuti con il computer CDC 7600. Nel 1982 i giapponesi Yoshiaki Tamura e Yasumasa Kanada calcolarono 8.388.608 cifre in meno di 30 ore sfruttando un Hitachi M-280H; nel 1988 Kanada si migliorò arrivando 201.326.000 cifre calcolate in 6 ore utilizzando un Hitachi S-820, e nel 1995 giunse addirittura a 6 miliardi di cifre. Dopo che nel 1996 David Chudnovsky e Gregory Chudnovsky avevano raggiunto gli 8 miliardi di cifre, l'attuale record spetta ancora a Yasumasa Kanada, che nel 2002 calcolò 1.241,1 miliardi di cifre grazie a 25 giorni di lavoro di un Hitachi SR8000/MPP a 64 nodi; finora nessuno ha saputo fare di meglio. Nel suo romanzo "Contact" (1985), lo scienziato Carl Sagan (1934-1996) ha immaginato che da un certo punto in poi le cifre di pi greco siano tutte zeri ed uni, e che, disponendo tali cifre in una matrice quadrata, gli uni disegnino appunto un cerchio, "la firma dell'artista", cioè l'impronta del Creatore nella Sua creazione.

Anche se la rettificazione della circonferenza con riga e compasso è impossibile, come dimostrato da Lindemann, esistono varie costruzioni approssimate di un segmento la cui lunghezza differisce di pochissimo da quella della circonferenza. Una delle più accurate è la costruzione di Wilhelm Specht (1907-1985), che si effettua come segue. Sulla la circonferenza di centro O e raggio r si prende un punto A e si traccia la tangente in A alla circonferenza. Su tale circonferenza si prendono i segmenti AB = 2r, BC = r/5, CD = 2r/5. Si congiunge O con C e D, e sulla retta AO si riporta, a partire da A, un segmento AE = OC. Dal punto E si traccia la retta parallela a OD, che interseca la retta AC in F, come segue:

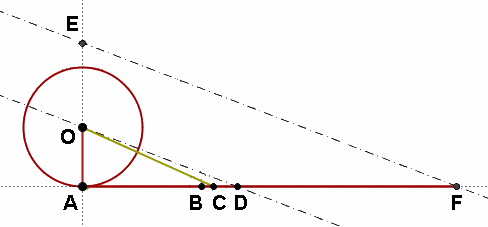
Si ha AC = 2r + r/5 = 11r/5, AO = r, e per il teorema di Pitagora applicato al triangolo rettangolo AOC:

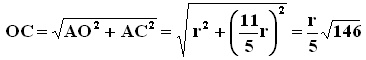
Ora, i triangolo OAD ed EAF sono simili avendo i lati paralleli, e quindi vale la proporzione:

E siccome π = 3,1415929..., effettivamente la costruzione di Specht fornisce la circonferenza rettificata con un errore per difetto minore di 1/1.000.000 del raggio!

Dante sembra avere sentore del fatto che questa sorta di "corsa alle cifre decimali di pi greco", iniziata agli albori della storia umana, avrebbe rappresentato una sfida per i matematici di ogni epoca, a giudicare da quanto egli dice alla fine del proprio viaggio ultraterreno:

« Qual è il geometra che tutto s'affige
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige,
tal era io a quella vista nova;
veder volea come si convenne
l'imago al cerchio e come vi si indova » (Par. XXXIII, 133-138)

Sembra di vederlo, questo geomètra del Medioevo, che combatte con i calcoli (« tutto s'affige », un verbo che dà proprio l'immagine dello spremersi le meningi) allo scopo di misurare il cerchio, eppure non riesce a trovare il principio di cui manca (latino "indiget") per risolverlo, vale a dire proprio il nostro . Questa non è la prima occasione in cui Dante rievoca l'antichissimo problema della rettificazione della circonferenza, ormai divenuto uno dei simboli dell'impossibilità umana di conoscere tutto: il nostro autore ne aveva parlato già nel Convivio:

« La Geometria si muove intra due repugnanti a essa, sì come 'l punto e lo cerchio - e dico "cerchio" largamente ogni ritondo, o corpo o superficie -; chè, sì come dice Euclide, lo punto è principio di quella, e, secondo che dice, lo cerchio è perfettissima figura in quella, che conviene però avere ragione di fine. Sì che tra 'l punto e lo cerchio sì come tra principio e fine si muove la Geometria, e questi due a la sua certezza repugnano; che lo punto per la sua indivisibilità è immensurabile, e lo cerchio per lo suo arco è impossibile a quadrare perfettamente, e però è impossibile a misurare a punto. » (Convivio II, XIII, 26-27)

« Infatti lo studioso di geometria ignora la quadratura del cerchio » (III, III).

Stavolta però il riferimento all'impossibile quadratura del circolo non è certo casuale: ci troviamo nell'ultimo Canto del Paradiso, al sommo dell'Empireo, e la « vista nova » (cioè la straordinaria visione) che Dante si trova di fronte è Dio stesso. Grazie alle preghiere di San Bernardo, la Vergine Maria ha acconsentito che Dante potesse spingere il suo sguardo fin dentro il Mistero altissimo della Trinità Divina. E così, man mano che la sua vista si potenziava, il pellegrino celeste ha visto apparire il Padre, il Figlio e lo Spirito Santo sotto forma di tre cerchi (ecco perchè la similitudine del geomètra non è scelta a caso!), « di tre colori e d'una contenenza » (Par. XXXIII, 117), cioè di diverso colore ma di uguale raggio, perchè le Tre Persone della Santissima Trinità sono della stessa Natura ma diverse nei loro attributi. Ad una osservazione ancora più acuta, « la circulazion che sì concetta / pareva in Te come lume reflesso » (Par. XXXIII, 127-128), cioè il cerchio del Figlio che viene generato dal Padre come il riflesso generato da uno specchio, appare a Dante dipinto dentro di sé, del suo stesso colore, con l'immagine dell'uomo. È questo il Mistero dell'Incarnazione, che Dante con le sole forze della sua ragione non può riuscire a penetrare, esattamente come il geometra non riuscirà mai a rettificare il cerchio. Ciò che Dante vuole trasmettere al lettore è il vero e proprio dramma dell'intellettuale, che "tutto s'affige", tenta e ritenta, ma deve ad un certo punto ammettere i limiti delle proprie capacità razionali. Qui possiamo avvertire la partecipazione sincera di Dante, che per primo ha dovuto affrontare questa consapevolezza, per primo ha cercato di confutarla, e che per primo ha dovuto infine abbassare il capo e accettarla, aprendosi solo così la strada verso una realtà più alta. Dante ha capito che la sola razionalità dell'uomo non può consentirgli di raggiungere le verità ultime, ha sperimentato il profondo scoramento che deriva dalla scoperta di questo limite umano, e lo ricorda in più passi della commedia, dall'innegabile simpatia che prova nei confronti di Ulisse, colui dentro il quale nulla poté vincere « l'ardore a divenir del mondo esperto », fino a quest'ultima sofferta visione del geometra che si affanna dietro l'impossibile. Evidentemente il Ghibellin Fuggiasco vedeva nella Matematica e mella Geometria il più alto grado di perfezione raggiungibile dalla sola ragione umana: che essa giunga al fallimento e debba essere superata è insito nel limite dell'uomo e nulla toglie al valore della speculazione scientifica.

La Visione di Dio, Nino e Silvio de Gregori, dall'edizione del
"Paradiso" di "Famiglia Cristiana", Società San Paolo, 1992

C'è però chi, nell'analisi del « geometra che tutto s'affige / per misurar lo cerchio », ha voluto vedere non solo una brillante similitudine dantesca, ma anche un'allusione nemmeno troppo velata al fatto che solo Dio conosce il segreto della quadratura del cerchio. Si considerino infatti gli ultimi 22 versi del Paradiso, e li si suddivida nel seguente modo:

« O luce etterna che sola in te sidi,
sola t'intendi, e da te intelletta
e intendente te ami e arridi!
Quella circulazion che sì concetta
pareva in te come lume reflesso,
da li occhi miei alquanto circunspetta,
      dentro da sé, del suo colore stesso,
     mi parve pinta de la nostra effige:
     per che 'l mio viso in lei tutto era messo.
     Qual è 'l geomètra che tutto s'affige
          per misurar lo cerchio, e non ritrova,
          pensando, quel principio ond'elli indige,
     tal era io a quella vista nova:
     veder voleva come si convenne
     l'imago al cerchio e come vi s'indova;
     ma non eran da ciò le proprie penne:
se non che la mia mente fu percossa
da un fulgore in che sua voglia venne.
A l'alta fantasia qui mancò possa;
ma già volgeva il mio disio e 'l velle,
sì come rota ch'igualmente è mossa,
l'amor che move il sole e l'altre stelle. » (Par. XXIII, 124-145)

Come si vede, essi appaiono manifestamente simmetrici rispetto alla coppia centrale di versi, evidenziata in azzurro, che poi sono quelli che racchiudono il segreto della misura del cerchio e del "principio" di cui tutti i matematici umani difettano. Questi versi sono inoltre al centro di un gruppo di 10 versi che comincia con « dentro da sé », cioè con il mistero della Divinità, e termina con « non eran da ciò le proprie penne », simbolo dell'impotenza umana a penetrare dentro quell'ineffabile mistero con i soli, poveri mezzi della sua ragione. All'interno di questi due versi, che ho evidenziato in rosso, vi è prima una terna di versi che espone l'inestricabile mistero di un cerchio nel quale è rappresentata « la nostra effige » umana, cioè la nostra forma corporea con un tronco, una testa, due braccia e due gambe. In posizione simmetrica vi è un'altra terna di versi che contiene la similitudine dantesca fra la chiara visione di una forma umana combaciante con la forma perfetta e regolare del cerchio, e l'incapacità da parte di Dante, nonostante il fatto che le sue virtù percettive e cognitive si siano potenziate man mano che saliva verso Dio, a risolvere quel problema. Ho evidenziato tali versi in verde. E non è finita qui, perchè i sei versi che precedono il primo evidenziato in rosso rappresenta il momento esatto in cui Dante può finalmente fissare gli occhi nel mistero di Dio, in quella luce eterna che solo da Se medesima può essere contenuta (« sola in te sidi ») e vedersi compiutamente: in quanto comprende Se stessa (« sola t'intendi ») è il Padre, in quanto è compresa da Se stessa (« e da te intelletta ») è il Figlio, e in quanto ama Se stessa (« intendente te ami e arridi ») è lo Spirito Santo. D'altro canto, gli ultimi sei versi che seguono il secondo verso evidenziato in rosso, simmetrici rispetto ai suddetti, esprimono il fatto che solo attraverso l'illuminazione suprema della Grazia, l'Alighieri può raggiungere la chiara visione del Mistero Divino (« in che sua voglia venne »), ma un attimo dopo essa è già svanita, poiché la fantasia e la memoria umane non sono in grado di catturarla, e l'Amore che muove tutto l'universo placava la sua ansia di sapere e il suo anelito volitivo, come una ruota che si muove di moto circolare uniforme intorno al suo asse. Questi gruppi di versi li ho evidenziati in giallo. La simmetria è perfetta: sopra l'oggetto del desiderio, sotto l'appagamento dello stesso, pur nella forma imperfetta che è consentita a Dante dalla sua mortalità.

Insomma, questi ultimi 22 versi somigliano davvero nella loro struttura ad un cerchio, fatto a sua volta di tre anelli concentrici, esattamente come la visione che Dante può avere di Dio Uno e Trino! Quello più esterno è quello evidenziato qua sopra in giallo, formato dai versi 124-129 e 140-145, corrisponde allo Spirito Santo ed infatti contiene l'ardore che Dante ha di conoscere la Natura Divina e l'appagamento che essa porta, il che può essere solo il risultato di una illuminazione da parte dello Spirito Santo (siccome di tale cerchio Dante dice « parea foco / che quinci e quindi igualmente si spiri », io l'ho evidenziato con il giallo, che è il colore del Sole). Il cerchio intermedio è quello formato dai versi 130-133 e 136-139, evidenziato in rosso e in verde, e corrisponde a Dio Figlio: infatti in esso si parla della « nostra effige » che Cristo vestì incarnandosi, e dell'« imago » che « s'indova » al cerchio, simbolo visivo delle Due Nature di Cristo Uomo e Dio (infatti anch'io ho usato due colori per evidenziare questi versi!). Infine, il cerchio più interno è quello costituito dai due soli versi 134-135, da me evidenziati in azzurro, che rimanda istintivamente a Dio Padre (ho usato quel colore perchè noi lo chiamiamo "il Padre Celeste"!), poiché contiene il mistero del « principio ond'elli indige », il pi greco che, essendo formato da infinite cifre ed essendo irrazionale e trascendente, solo da Dio può essere colto nella sua interezza, richiamando la misteriosa citazione evangelica: « nessuno lo sa, neppure gli angeli del cielo, neppure il Figlio, ma solo il Padre » (Mt 24, 36; Mc 13, 32)!

Dopo questo excursus nelle scienze astratte, siamo ormai pronti per verificare quali riferimenti fa Dante nella sua opera alle scienze applicate. Per partire dalla Geologia, cliccate qui e proseguite nel nostro itinerario.