![]()
|
«
Grande è il Signore e degno di ogni lode; (Salmo 145, 3) |
Sembra impossibile parlare di matematica nella Bibbia senza dire qualcosa del concetto di infinito, dal momento che non si contano i versetti in cui ci si rivolge a qualcosa di « senza fine ». Naturalmente, infinito per antonomasia è YHWH con tutte le Sue qualità:
« Grande è il Signore e degno di ogni lode;
senza fine è la
Sua grandezza. » (Sal 145, 3)
« Di ogni cosa perfetta ho visto il
confine:
l'ampiezza dei Tuoi comandi è
infinita. » (Sal 119, 96)
« Secca l'erba, appassisce il fiore,
ma la parola del nostro Dio dura
per sempre. » (Is 40, 8)
« Ci hai forse rigettati per sempre,
e senza limite
sei sdegnato contro di noi? » (Lam 5, 22)
Anche Dante nel suo Purgatorio non può esimersi dall'usare il medesimo aggettivo per qualificare Dio, che si concede alle anime che ardono d'amore così come un raggio di sole verso un corpo che è capace di rifletterlo:
« Quello
infinito
e ineffabil bene
che là sù è, così corre ad amore
com'a lucido corpo raggio vene. » (Purg. XV, 67-69)
Invece in altri versetti è detta infinita la gioia dei giusti che confidano nell'aiuto divino:
« Gioiscano quanti in te si rifugiano,
esultino senza fine.
Proteggili, perché in te si allietino
quanti amano il tuo nome. » (Sal 5, 12)
« Vi ho lasciati andare con dolore e
pianto,
ma Dio vi ricondurrà a me
con letizia e gioia, per sempre.
» (Bar 4, 23)
Nei seguenti passi infinita è la letizia dei Santi nel Regno di Dio, indicata nel Salmo 16 con la metafora dell'"a destra del Signore" che utilizzerà anche Gesù:
« Mi indicherai il sentiero della vita,
gioia piena alla tua presenza,
dolcezza senza fine alla tua destra.
» (Sal 16, 11)
« I saggi risplenderanno come lo splendore del firmamento; coloro che avranno indotto molti alla giustizia risplenderanno come le stelle per sempre. » (Dn 12, 3)
« Poiché come avete bevuto sul mio Monte
Santo,
così berranno tutte le nazioni senza fine
» (Abd 1, 16)
Altrove nella Scrittura ad essere illimitata è la fedeltà dei Santi:
« Su di te mi appoggiai fin dal grembo materno,
dal seno di mia madre sei tu il mio sostegno:
a te la mia lode senza fine.
» (Sal 71, 6)
« Ho piegato il mio cuore a compiere i tuoi decreti,
in eterno, senza fine.
» (Sal 119, 112)
« Alleluia! Benedetto il Dio d'Israele
e benedetti coloro che benedicono il suo santo nome
nei secoli e per sempre!
» (Tb 13, 18)
Illimitata nel tempo è anche la promessa del trono per la dinastia davidica, che verrà resa eterna da Gesù Cristo:
« Non ritirerò il mio amore, come l'ho ritirato da Saul, che ho rimosso di fronte a te. La tua casa e il tuo regno saranno saldi per sempre davanti a te, il tuo trono sarà reso stabile per sempre. » (2 Sam 7, 16)
« Non temere, Maria, perché hai trovato grazia presso Dio. Ed ecco, concepirai un figlio, lo darai alla luce e lo chiamerai Gesù. Sarà grande e verrà chiamato Figlio dell'Altissimo; il Signore Dio gli darà il trono di Davide suo padre e regnerà per sempre sulla casa di Giacobbe, e il suo regno non avrà fine. » (Lc 1, 30-33)
« Egli invece, poiché resta per sempre, possiede un sacerdozio che non tramonta. » (Eb 7, 24)
Altrove invece il termine "infinito" è usato in modo iperbolico, a significare un numero impossibile da quantificare in modo preciso:
« I tuoi occhi vedranno un re nel suo
splendore,
contempleranno una terra
sconfinata. » (Is 33, 17)
« [Nabucodonosor] fece quindi ritorno a Ninive con tutto l'insieme delle sue truppe, che era una moltitudine infinita di guerrieri, e si fermò là, egli e il suo esercito, oziando e banchettando per centoventi giorni. » (Gdt 1, 16)
« "Saccheggiate l'argento, saccheggiate
l'oro".
Ci sono tesori infiniti,
ammassi d'oggetti preziosi! » (Na 2, 10)

Guerrieri assiri in un bassorilievo del VII secolo a.C. oggi al British Museum di Londra
In diversi passi l'Autore Sacro utilizza invece la metafora delle "mille generazioni" per indicare un arco di tempo illimitato (se una generazione dura una trentina d'anni, "mille generazioni" equivale alla bellezza di 300 secoli!)
« Io, il Signore tuo Dio, sono un Dio geloso, che punisce la colpa dei padri nei figli fino alla terza e alla quarta generazione per coloro che mi odiano, ma che dimostra la sua bontà fino a mille generazioni, per quelli che mi amano e osservano i miei comandamenti. » (Es 20, 6)
« Ricordate sempre la sua alleanza,
parola data per mille generazioni
» (1Cr 16, 15)
« Tu usi bontà con mille generazioni e fai scontare l'iniquità dei padri in seno ai figli dopo di loro; tu sei un Dio grande e forte, il cui nome è Signore degli eserciti. » (Ger 32, 18)
Queste citazioni sono sicuramente più che sufficienti per comprendere l'importanza del concetto di infinito fin dagli albori della civiltà umana, molto prima dunque che iniziasse la gloriosa storia della matematica greca. Così infatti si esprime il grande matematico tedesco David Hilbert (1862-1943): « Da tempo immemorabile l'infinito ha suscitato le passioni umane più di ogni altra questione. E' difficile trovare un'idea che abbia stimolato la mente in modo altrettanto fruttuoso, tuttavia nessun altro concetto ha più bisogno di chiarificazione. » Ed Hermann Weyl (1885-1955) si spinse ad aggiungere: « La matematica è la scienza dell'infinito »! Per questo, noi dedicheremo questa lezione proprio a chiarire taluni aspetti dell'idea di infinito.
Tale concetto, pur già chiaro alla mente del Re Davide nel X secolo avanti Cristo quando scrive « Il timore del Signore è puro, rimane per sempre » (Salmo 19, 10a), fu formalizzato per la prima volta dal filosofo greco Anassimandro di Mileto (610-546 a.C.), che pose come origine del mondo un principio, materiale sì, ma infinito, illimitato, indeterminato, immortale, indistruttibile, chiamato apeiron (in greco "senza limiti"). Così egli infatti si esprime, secondo quanto ci ha tramandato il filosofo neoplatonico Simplicio: « il principio non è né l'acqua né un altro dei cosiddetti elementi, ma un'altra natura infinita, dalla quale provengono tutti i cieli e i mondi che in essi esistono ». Al contrario, Parmenide di Elea (515-450 a.C.) affermò drasticamente che l'infinito non esiste, come conseguenza della immobilità dell'Uno da lui concepito. Anche la scuola pitagorica rifiutava il concetto di infinito, sulla base di uno dei suoi dogmi (tale scuola si configurava come una vera e propria scuola religiosa), secondo cui l'essenza di tutte le cose è spiegabile in termini dei numeri interi e dei loro rapporti. Essi credevano che i corpi fossero costituiti di corpuscoli tutti uguali tra loro e disposti in forme geometriche; secondo loro, insomma, i punti avrebbero un'estensione non nulla, per quanto piccolissima (contrariamente a quanto affermerà Euclide, per il quale « il punto è ciò che non ha parti »), e quindi un segmento dovrebbe essere formato da un numero finito di punti, per quanto grandissimo. Pertanto il rapporto di due segmenti dovrebbe risultare uguale al rapporto di numeri interi che esprimevano quante volte il punto sarebbe contenuto in ciascuno dei due segmenti; il punto quindi dovrebbe essere il sottomultiplo comune a tutti i segmenti, che risulterebbero tutti tra loro commensurabili. Per questo la scoperta dei numeri irrazionali, conseguente all'applicazione del Teorema di Pitagora al triangolo rettangolo isoscele per determinarne l'ipotenusa, fu un duro choc, e per questo tentarono in ogni modo di tenerla segreta; secondo la leggenda il filosofo pitagorico Ippaso di Metaponto, per aver svelato al mondo l'esistenza delle grandezze incommensurabili e quindi dei numeri irrazionali, fu punito dagli déi morendo in un naufragio.
L'infinito dunque entrò nella Matematica fin dalle origini, a partire dal concetto stesso di numero naturale, appartenente all'insieme N. I numeri naturali infatti, che sono i più semplici, sono ordinati, ed ognuno di essi si può ricavare dal precedente aggiungendogli un'unità. Ma questo, per l'appunto, può essere ripetuto illimitatamente, dal che ne consegue la seguente proprietà: fissato comunque un numero naturale è sempre possibile trovare un numero maggiore di esso. Il filosofo tedesco Immanuel Kant (1724-1804) nella settima sezione della sua "Critica della Ragion Pura" (1781) chiamava « progressus in indefinitum » questo "infinito per addizione" che « non ammette nessuna limitazione se non quella provvisoria che gli può essere assegnata ad ogni suo passo, prima di procedere al passo successivo ». Ovviamente tale infinito è irraggiungibile, non potendosi contare effettivamente infiniti numeri naturali, e per questo un altro grande filosofo greco, Aristotele (384-322 a.C.), affermava che « il numero è infinito in potenza, ma non in atto ». I numeri naturali possono essere rappresentati con una serie di punti equidistanti, che si susseguono senza fine lungo la retta; è quella che oggi chiamiamo una successione infinita discreta, perchè tra due elementi consecutivi c'è uno spazio vuoto, da intendersi come assenza di elementi. Si parla anche di un'infinità numerabile, giacché di questi infiniti elementi è possibile dire qual è il primo, il secondo, il terzo, e così via.
La prima dimostrazione che include il concetto di infinito la dobbiamo ad Euclide (III secolo a.C.), che nel Libro IX, proposizione 20 dei suoi celebri "Elementi" riuscì brillantemente a dimostrare l'infinità dei numeri primi. Per far questo, ragionò nel seguente modo. Si prenda l'insieme dei numeri primi 2, 3, 5, 7, 11, 13, 17, 19... e si ammetta per assurdo che esista un numero primo N maggiore di tutti. Consideriamo allora il numero G = ( 2 x 3 x 5 x 7 x 11 x ... x N ) + 1, ottenuto moltiplicando tra loro tutti i numeri fino ad N e sommando 1 al risultato. Se G non è primo, allora ammette sicuramente un divisore primo k diverso da uno. Ma tale numero primo è sicuramente compreso tra quelli che abbiamo moltiplicato tra loro per ottenere G, e dunque divide il prodotto 2 x 3 x 5 x 7 x 11 x ... x N. Allora k deve dividere anche 1, il che è chiaramente assurdo. Conclusione: G è necessariamente primo. Ad esempio, ( 2 x 3 x 5 x 7 x 11 ) + 1 = 2311 che è primo, come si evince da questa pagina. Ma G è certamente maggiore di N, per cui N non è il numero primo maggiore di tutti. E potendosi questo ragionamento ripetere quante volte si vuole, se ne conclude che l'insieme dei numeri primi è infinito, ed è anche numerabile, potendosi dire qual è il primo, il secondo, il terzo, eccetera.
Noi però sappiamo che non esistono solo i numeri naturali e il loro "infinito per addizione": basta considerare l'insieme Q dei numeri razionali. Infatti esso non è discreto, ma denso, perché tra due numeri razionali, per quanto vicini, vi sono sempre infiniti altri numeri razionali. Ad esempio, sono infiniti i numeri razionali compresi tra 0 ed 1, che possono essere rappresentati come frazioni proprie, con il numeratore minore del denominatore. Se consideriamo il segmento unitario di estremi 0 ed 1, sembra un paradosso che questo segmento di misura finita possa contenere infiniti punti, eppure questa è proprio una delle caratteristiche della retta come è stata definita da Euclide: si tratta solo del primo tra i numerosi paradossi riguardanti l'infinito con cui ci scontreremo in questa breve sintesi. Come si vede, l'infinito associato ai numeri razionali è un infinito ottenuto non per addizione ma per divisione, e la caratteristica di questo infinito, che nella nona sezione della sua "Critica della Ragion Pura" Kant chiamava « regressus in infinitum », è che esso è interamente contenuto in un intervallo limitato come un segmento, suddiviso all'infinito in parti sempre più piccole. Secondo Kant la differenza tra progressus e regressus in infinitum sta proprio nel fatto che nel primo caso gli infiniti elementi vanno cercati al di fuori della totalità parziale, sempre finita, che non si cessa mai di ottenere; nel secondo essi vanno trovati all'interno di esso, ed esistono già prima della suddivisione, così come esistono i punti di un segmento prima ancora di suddividerlo.
La lemniscata di Bernoulli, una curva che ricorda nella sua forma il simbolo dell'infinito
Per comprendere le difficoltà dei matematici greci a comprendere pienamente il concetto di infinito, basta pensare al paradosso di Zenone del quale abbiamo parlato nella lezione dedicata alle progressioni geometriche. Secondo i matematici antichi, è inconcepibile che la somma di infiniti termini possa convergere ad un risultato finito, e dunque Achille (o il suo equivalente ebraico) non dovrebbe superare mai la proverbiale tartaruga, anche se ciò è in palese contraddizione con il senso comune. Un'altra difficoltà i Greci la incontrarono quando cercarono di risolvere il problema della quadratura del cerchio, del quale abbiamo invece parlato nella lezione dedicata al pi greco. Com'è noto, Antifonte di Atene (480-410 a.C.), Eudosso di Cnido (408-355 a.C.) e Archimede di Siracusa (287-212 a.C.) affrontarono il problema utilizzando il cosiddetto "metodo di esaustione", un vero e proprio precursore dell'Analisi Infinitesimale. Tale metodo consiste nel calcolare l'area di una figura piana costruendo una successione di poligoni che convergono alla figura data; in tal modo, l'area cercata è il limite della successione delle aree di quei poligoni. Archimede in particolare cercò di misurare l'area del cerchio approssimandola con una successione di poligoni regolari inscritti con un numero crescente di lati, fino ad esaurire (da cui il termine "esaustione") tutta la superficie all'interno del circolo. Partendo da un triangolo equilatero e raddoppiando progressivamente il numero dei lati, Archimede giunse fino al poligono di 96 lati e determinò che 223/71 < π < 22/7. Tuttavia, è possibile sostenere che "all'infinito" i poligoni si identificheranno con il cerchio e che i loro lati potranno essere considerati archi "infinitesimi" della circonferenza? Se è così, il cerchio va inteso come un poligono con un numero infinito di lati, e dunque dovremmo accettare il fatto di aver "raggiunto l'infinito". Per questo Aristotele contestò le affermazioni di Antifonte, sostenendo che l'insieme dei poligoni inscritti nella circonferenza è un insieme illimitato, nel senso che per ogni poligono con un numero comunque elevato di lati ne esisterà un altro con un numero di lati ancor più elevato, che non potrà coincidere con la circonferenza perché ammetterà dopo di sé un ulteriore poligono con un numero di lati ancora maggiore. Insomma, l'infinito non verrà mai raggiunto.
Nel mondo greco il dibattito sull'infinito apparve, con accenti modernissimi, anche nell'esplorazione (a quei tempi solo mentale) della struttura intima della materia, fin da quando Democrito di Abdera (460-370 a.C.) propose che l'operazione di suddivisione della materia in parti più piccole non può procedere all'infinito, ma solo fino a che si raggiunge la particella più piccola, l'elementare e indivisibile atomo. Gli atomi si muovono secondo Democrito in un vuoto privo di materia e si aggregano e disgregano casualmente dando origine a tutte le realtà, secondo un rigido meccanicismo secondo il quale nulla si crea e nulla si distrugge; opinione, questa, che fece dire di lui a Dante Alighieri: « Democrito che 'l mondo a caso pone » (Inf. IV, 136) Proprio l'impossibilità di dividere la materia all'infinito è stato uno dei pilastri sui quali è cresciuta la Fisica Moderna, ed è quanto mai attuale nei dibattiti che ancor oggi sopravvivono nella moderna Meccanica Quantistica: particella o onda? Vuoto classico o vuoto quantistico? Unicità o molteplicità degli universi? A proposito delle opinioni fra loro opposte di Democrito e Aristotele, il famoso matematico Lucio Lombardo Radice (1916-1982) ha scritto: « È qui evidente un problema fondamentale risolto da Cantor nell'Ottocento: è possibile solo una suddivisione del continuo in un numero quanto si voglia grande di parti, oppure si può pensare il continuo come una infinità di componenti ultime, altissime, indivisibili? »
Il primo a mettere in discussione il concetto di infinito così come era stato elaborato dalla filosofia greca fu il teologo francescano Guglielmo di Occam (1295-1349), il quale, anticipatore in moltissimi campi delle idee moderne, sostenne che non è impossibile che la parte di una grandezza non sia minore del tutto: infatti « ciò accade ogni qualvolta una parte del tutto è infinita... » (Scienze nuove, Op., VIII, pag. 79). In questo, egli precorse una visualizzazione dell'infinito che solo alla fine dell'ottocento, come vedremo, verrà utilizzata dai matematici per caratterizzare gli insiemi infiniti. Il tedesco Nicolò Cusano (1401-1464) andò al di là, parlando del cerchio come di un poligono con infiniti lati, e postulando per primo l'infinità dell'universo. Cusano considerò la rotazione, attraverso la quale si genera il cerchio, il processo che maggiormente riflette nel mondo empirico il processo attraverso il quale l'universo è stato generato; egli inoltre parlò di Dio come dell'infinito in cui gli opposti vengono a coincidere, e del mondo come dell'"explicatio" (esplicazione) di Dio nella molteplicità e di una "imitazione" della divinità. Seguendo tale idea il mondo non può che essere infinito e privo di centro, e così Cusano fu il primo a rifiutare la cosmologia aristotelica; andò persino al di là di Copernico, il cui universo era finito, e pur sempre limitato dalla sfera delle stelle fisse! A Cusano si richiamò poi Giordano Bruno (1548-1500), autore del dialogo "De l'infinito, universo e mondi" (1584), in cui si immagina un colloquio tra Elpino, portavoce della tradizionale filosofia aristotelica, e Filoteo, alter ego di Bruno stesso, per il quale « uno è il cielo, il spacio immnso, il seno, il continente universale, l'eterea regione per la quale il tutto discorre e si muove. Ivi innumerabili stelle, astri, globi, soli e terre sensibilmente si veggono, et infiniti ragionevolmente si argumentano. » Il filosofo di Nola, insomma, non si limitava a sostenere il modello copernicano, ma mirava a un universo "infinito in atto", per usare il lessico aristotelico, in quanto « effetto unico e totale dell'infinita potenza, bontà, volontà divina ».
Cusano e Bruno tuttavia non erano matematici. Chi diede seguito alle intuizioni di Occam nel campo dei numeri fu il grande Galileo Galilei (1564-1642), il quale postulò la possibilità di ridurre un insieme continuo e limitato come un segmento in infiniti elementi infinitesimi e indivisibili. Poiché un segmento può essere diviso in quante parti si vuole ancora divisibili, si deve necessariamente ammettere che esso sia composto da infinite parti, ma se queste parti sono infinite allora devono necessariamente essere prive di estensione, perché infinite parti estese hanno un'estensione infinita, mentre il segmento ha un'estensione limitata. Siccome è possibile "piegare" un segmento per formare un qualunque poligono regolare con un qualsiasi numero di lati, allora piegandolo a formare un cerchio si può benissimo dire di "aver raggiunto l'infinito" e di poter davvero considerare la circonferenza come un poligono con un numero infinito di lati, contro il ragionamento di Aristotele.
Galilei fu però anche il primo a rendersi conto dei problemi che nascono dal giocare con l'infinito, avendo elaborato dei paradossi che non riuscì a risolvere. Questo lo portò ad affermare che « queste son di quelle difficoltà che derivano dal discorrer che noi facciamo col nostro intelletto finito intorno a gl'infiniti, dandogli quelli attributi che noi diamo alle cose finite e terminate; il che penso che sia inconveniente... » Il più celebre tra i paradossi proposti da Galileo è quello dei numeri pari. Consideriamo i numeri naturali { 1, 2, 3, 4, 5, 6, 7... } e i loro doppi { 2, 4, 6, 8, 10, 12, 14... }, che poi sono tutti i numeri pari. I doppi dei naturali sono anch'essi dei numeri naturali, ma è evidente che sono solo un sottoinsieme di N: per la precisione, sono la metà di essi. È però possibile stabilire una corrispondenza biunivoca tra N e l'insieme dei numeri naturali pari, cioè una corrispondenza nella quale ad ogni numero naturale corrisponda uno ed un solo numero pari che è il suo doppio: a 1 corrisponde 2, a 2 corrisponde 4, a 3 corrisponde 6, e così via: si dice che i due insiemi sono equipotenti. Ma due insiemi equipotenti devono avere necessariamente lo stesso numero di elementi, dato che ad ogni elemento del primo corrisponde uno ed un solo elemento del secondo. I numeri pari sono perciò tanti quanti i numeri naturali: ciò significa che una parte può essere numericamente uguale al tutto, in evidente contrasto con il senso comune. La stessa cosa vale per i multipli di tre, di quattro, di dieci, per i quadrati dei numeri interi, per i cubi, e così via: l'insieme N risulta numericamente uguale a tutti questi suoi sottoinsiemi.

Siccome Galileo è considerato il fondatore della fisica moderna, non poteva mancare un esempio tratto dal mondo della meccanica, il cosiddetto paradosso delle ruote. Si considerino dunque due ruote concentriche, tali che la maggiore rotoli sopra una guida rettilinea AB e la minore su una guida rettilinea CD, con la stessa lunghezza di AB, come si vede nella figura soprastante. Facendo compiere un giro completo alla circonferenza maggiore fino a D, la minore arriverà al punto B. Ma CD = AB. « Or come dunque può senza salti scorrere il cerchio minore una linea tanto maggiore della sua circonferenza? » si chiede Galileo. Anche in questo caso ciò è dovuto alla possibilità di stabilire una corrispondenza biunivoca tra la circonferenza maggiore e quella minore, e quindi tra un segmento ed una sua parte propria: basterà infatti proiettare dal comune centro i punti della circonferenza minore su quelli della maggiore!
Galileo non riuscì a trovare una soluzione ai suoi paradossi, e questo fatto lo portò a negare la possibilità di indagare matematicamente l'infinito: « quando siamo tra gl'infiniti e gl'indivisibili, quelli [gl'infiniti] sono incomprensibili dal nostro intelletto finito per la loro grandezza, e questi [gl'indivisibili] per la loro piccolezza. » Ma gli anni in cui Galileo visse, caratterizzati dalla grande "rivoluzione scientifica" (così si chiama di solito il periodo compreso tra l’anno di pubblicazione del capolavoro di Copernico "De revolutionibus orbium coelestium", il 1543, e quello dell'opera di Newton "Philosophiae naturalis principia mathematica", il 1687), furono segnati anche da una vera e propria rivoluzione in campo matematico. La necessità di determinare la velocità e l'accelerazione di un punto materiale di cui è nota la legge oraria, di determinare i massimi e i minimi di una funzione data, nonché di determinare la somma di particolari somme infinite, condusse alla nascita del moderno calcolo infinitesimale. I primi procedimenti per il calcolo con gli infiniti e con gli infinitesimi erano già comparsi nel Cinquecento, e tra i precursori vanno ricordati il bolognese Pietro Antonio Cataldi (1552-1626), che elaborò la teoria delle frazioni continue, il boemo Johannes Kepler (1571-1630), che ricondusse il calcolo dell'area del cerchio alla somma delle aree degli infiniti triangoli isosceli aventi il vertice nel centro del cerchio e come base una corda infinitesima della circonferenza, e il milanese Bonaventura Cavalieri (1598-1647), discepolo dello stesso Galileo, che ideò il metodo degli indivisibili, usato per determinare aree e volumi, e quindi precursore del calcolo integrale. Un ruolo fondamentale lo giocò Evangelista Torricelli (1608-1647), lui pure discepolo di Galilei, il quale pervenne a un'altra considerazione paradossale studiando una figura geometrica particolare chiamata "Tromba di Gabriele", con riferimento al,'angelo che soffierà nella tromba per annunciare la fine del mondo:
« Il settimo angelo suonò la tromba e nel cielo echeggiarono voci potenti che dicevano: "Il regno del mondo appartiene al Signore nostro e al suo Cristo: egli regnerà nei secoli dei secoli. » (Ap 11, 15)
A dir la verità, da nessun parte dell'Apocalisse è scritto che a dare quel tremendo annuncio sarà l'Arcangelo Gabriele, ma il fatto che egli abbia annunciato la nascita di Giovanni Battista e di Gesù ha indotto la tradizione popolare ad identificare in lui l'angelo che suonerà la Settima Tromba. A lui è stata dedicata questa figura geometrica perchè, come tutto ciò che viene da Dio, anch'essa come si vede qui sotto ha estensione infinita:

Essa si ottiene prendendo in considerazione la curva di equazione y = 1/x (la comune iperbole equilatera), isolandone l'arco compreso tra + 1 e più infinito e facendolo ruotare di un giro completo attorno all'asse x. Utilizzando il metodo degli indivisibili, Torricelli dimostrò che tale figura geometrica, di estensione illimitata, incredibilmente ha volume finito ma superficie laterale infinita. Vediamo di fornire tale dimostrazione con la notazione moderna. Considerato l'arco di iperbole equilatera y = 1/x compreso fra + 1 e t, con t > + 1, si ha che il volume del solido di rotazione ottenuto facendolo ruotare attorno all'asse x è dato dall'integrale:
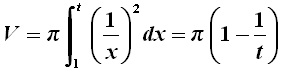
Ora, se t tende a diventare grandissimo, 1/t tende a diventare piccolissimo e scompare, per cui il volume del solido tende a π. In notazione moderna:
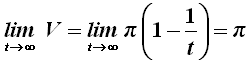
Invece la superficie laterale della Tromba di Gabriele è data dall'integrale:
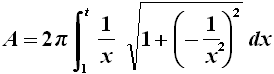
Questo integrale non può essere risolto alle quadrature, ma la radice è sicuramente maggiore di 1, per cui si può scrivere:
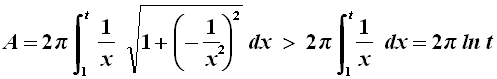
Ma, se t diventa grandissimo, anche ln t diventa grande a piacere (la funzione y = ln x è monotona crescente). Di conseguenza:
![]()
Torricelli si trovò così di fronte ad un "secchio" che può contenere una quantità finita di vernice (3,14 metri cubi), ma può essere dipinto all'esterno solo con una quantità di vernice infinita! Pensò di avere inciampato in un altro dei paradossi sull'infinito con cui aveva avuto a che fare Galileo, ma oggi sappiamo che non è così. Infatti l'integrale che porta al calcolo del volume di un solido di rotazione equivale alla somma dei volumi di infiniti cilindri di raggio decrescente e di spessore infinitesimo, mentre quello che porta al calcolo della superficie laterale equivale alla somma delle aree di infiniti anelli di raggio decrescente e di spessore infinitesimo. Alla luce del calcolo infinitesimale moderno, è facile rendersi conto che gli addendi della prima somma diminuiscono assai più rapidamente di quelli della seconda (più precisamente come 1/x2, anziché come 1/x), e questo spiega perchè la prima somma infinita converge a un valore finito, la seconda no. Torricelli comunque riuscì a dimostrare, sempre con il metodo degli indivisibili, che l'inverso non è possibile, cioè che non può esistere una figura di rotazione con superficie laterale finita ma volume infinito, un risultato comunque molto importante sulla strada dell'elaborazione del calcolo integrale.
Maurits Cornelis Escher, "Nastro di Möbius", xilografia, 1961
Contributi fondamentali alla nascita della moderna Analisi Matematica vennero nel seicento da Isaac Barrow (1630-1677), René Descartes detto Cartesio (1596-1650), Pierre de Fermat (1601-1665), Christiaan Huygens (1629-1695) e John Wallis (1616-1703); quest'ultimo è famoso per avere introdotto nel 1655 proprio il moderno simbolo dell'infinito, un 8 rovesciato in posizione orizzontale (che sarà universalmente utilizzato a partire dall'ottocento). Come si vede qui sopra, ad ispirare tale simbolo fu probabilmente il cosiddetto nastro di Möbius, una superficie dotata di una sola faccia che può essere interamente percorsa all'infinito senza mai attraversarne il bordo. Il grosso del bagaglio matematico del calcolo infinitesimale è però opera principalmente di Isaac Newton (1642-1727), il cui metodo delle flussioni è antesignano del calcolo differenziale, e Gottfried Wilhelm von Leibniz (1646-1716), ideatore del concetto di differenziale di una funzione e del moderno simbolo di integrale, pur in mancanza di fondamenti rigorosi. Nuovi metodi e modelli furono ideati nel XVIII secolo da Johann Bernoulli (1667-748), Leonhard Euler detto Eulero (1707-1783), Joseph-Louis Lagrange (1736-1813), Pierre-Simon de Laplace (1749-1827) e soprattutto da Augustin-Louis Cauchy (1789-1857) e da Karl Weierstrass (1815-1897), che giunsero ad una revisione critica dei fondamenti dell'analisi infinitesimale, cui conferirono un perfetto rigore logico sfruttando la definizione rigorosa di limite introdotta nel 1765 da Jean-Baptiste d'Alembert (1717-1783). Questa definizione permise di rimuovere definitivamente l'ultima difficoltà sulla strada dell'analisi matematica: l'infinito e l'infinitesimo "in atto" (per dirla con Aristotele) non si possono raggiungere, ma ci si può solo avvicinare indefinitamente ad essi. Non certo a caso, uno dei più grandi matematici della storia dell'uomo, Carl Friedrich Gauss (1777- 1855), in quegli anni affermò con decisione: « Devo protestare nel modo più deciso contro l'uso dell'infinito come qualcosa di compiuto, cosa che non è permessa in matematica. L'infinito non è che un façon de parler », cioè un modo di dire! Facciamo un esempio, considerando di nuovo la funzione 1/x, già protagonista nel caso della Tromba di Gabriele, e facciamo tendere x a zero. L'intuizione ci dice che, in questo caso, 1/x cresce oltre ogni limite. Si consideri allora un numero reale e positivo M, grande a piacere. Se 1/x cresce indefinitamente, allora potremo scrivere:
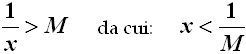
Ma, se M è grande a piacere, 1/M deve essere necessariamente piccolissimo. Ne consegue che, se x è compreso nella sottilissima striscia (in rosso nella figura sottostante) tra 0 e 1/M, la corrispondente y deve essere maggiore di M, e quindi compresa nella semistriscia evidenziata in giallo in questa figura:
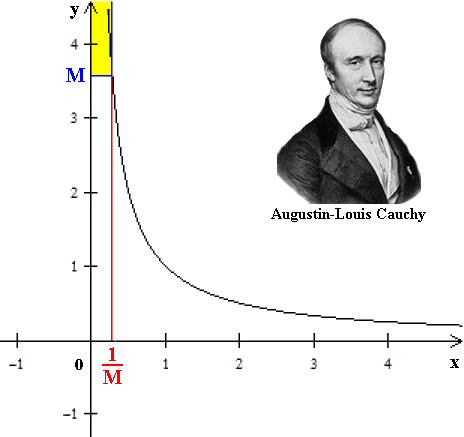
Se M aumenta, 1/M diminuisce, quindi la semistriscia gialla diventa sempre più alta e più stretta, ma i punti della funzione dovranno essere comunque contenuti in essa; la curva dunque è costretta ad avvicinarsi sempre di più all'asse delle y, ma ovviamente non lo raggiungerà mai. La y dunque non varrà mai più infinito, ma tenderà a più infinito, e ciò verrà espresso scrivendo:
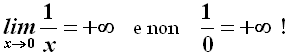
Il ragionamento seguito per giustificare quest'ultimo limite venne sistematizzato da Cauchy come segue. Sia data una funzione f(x). Si dice che essa tende al limite più infinito per x che tende a x0 se, fissato un numero reale M maggiore di zero e grande a piacere, esiste in corrispondenza di esso un δM maggiore di zero tale che, per qualunque x che dista da x0 meno di δM, il corrispondente f(x) è maggiore di M. Nell'esempio sopra riportato, naturalmente, x0 = 0 e δM = 1/M. Analogamente Cauchy definì il limite per x tendente a x0 di f(x) che tende ad l finito, il limite per x tendente ad infinito di f(x) che tende ad l finito e il limite per x tendente ad infinito di f(x) che tende ad infinito. Potete scaricare una sintesi di queste definizioni cliccando qui.
Come si vede, in questo modo l'infinito "in atto" è definitivamente rimosso dalla matematica e sdoganato una volta per tutte! A mettere nero su bianco in modo chiarissimo questo risultato è stato il matematico boemo Bernhard Bolzano (1781-1848) nel suo scritto postumo "Paradoxien des Unendlichen" ("I paradossi dell'infinito", 1851): « Che l'infinito sia contrapposto ad ogni mero finito è già espresso nel termine stesso. I matematici hanno fatto uso del termine infinito in altro senso che questo: se trovano una quantità maggiore di qualsiasi numero di unità assunte, la chiamano infinitamente grande; se trovano una quantità così piccola che ogni suo multiplo è minore dell'unità, la chiamano infinitamente piccola; né riconoscono alcuna altra specie di infinito oltre queste due e oltre specie da esse derivate, infinitamente più grandi o infinitamente più piccole, che discendono tutte dallo stesso concetto. » In questo saggio Bolzano anticipò di vari decenni le scoperte di Georg Cantor, delle quali parleremo tra poco. E un matematico contemporaneo, Claudio Bernardi (1948-), professore ordinario di matematica alla "Sapienza" di Roma, ha aggiunto: « Oggi in matematica si parla tranquillamente di infinito. Il ricorso all'infinito rende spesso addirittura più semplice lo studio della matematica: in particolare, la teoria delle derivate e degli integrali è più semplice e più potente della teoria delle differenze finite. » E non solo: aggiungendo a un piano euclideo i "punti all'infinito" o "punti impropri", si ottiene un "piano proiettivo" dove si enunciano proprietà generali senza eccezioni: due rette distinte hanno sempre uno ed un solo punto in comune, un punto al finito se sono incidenti, un punto all'infinito se sono parallele.
Un ulteriore, importante contributo venne dal matematico tedesco Julius Wilhelm Richard Dedekind (1831-1916), che nel 1872 pubblicò il saggio "Stetigkeit und irrationale Zahlen" ("Continuità e numeri irrazionali"), nel quale propose una soluzione ai due problemi che avevano messo in crisi l'infinito aristotelico: i numeri irrazionali e il "continuo". Dato infatti che i numeri razionali, come detto, sono "discreti", come si può realizzare una corrispondenza biunivoca con i punti della retta, che invece sono continui? Dedekind partì dall'osservazione che ogni numero razionale q divide l'insieme Q dei razionali in due insiemi detti classi: la classe Aq dei razionali tali che a < q e la classe Bq dei razionali tali che b > q. Dedekind chiamò quindi la coppia { Aq ; Bq } una sezione del campo razionale. Ogni numero di Aq è minore di ciascun numero di Bq, mentre q è il più grande numero di Aq o il più piccolo di Bq; esso risulta univocamente determinato dalla coppia { Aq ; Bq }, per cui si può dire che q sia identificato dalla coppia di classi { Aq ; Bq }.
Ma non sempre una sezione dei razionali individuata dalla coppia { Aq ; Bq } individuare un numero razionale, così come ad una sezione (cioè ad un punto) della retta non sempre corrisponde un numero razionale. Ogni volta che ciò accade, pensò Dedekind, è legittimo, "creare" un nuovo numero p che corrisponda alla coppia { Ap ; Bp }, cioè che sia esso stesso la coppia { Ap ; Bp }. Tale numero p è irrazionale.
Facciamo come sempre un esempio. Sia la sezione del campo razionale { Ap ; Bp } formata dalle due classi Ap e Bp tali che il quadrato di tutti i numeri di Ap è minore di 2, mentre il quadrato di tutti i numeri di Bp è maggiore di 2. Come è facile verificare, le due classi sono separate non da un numero razionale ma da un numero reale, che è la radice di 2. I numeri irrazionali "riempiono" esattamente i "buchi" lasciati nella retta dall'insieme Q, e permettono di realizzare una corrispondenza biunivoca tra i punti della retta e i numeri reali dell'insieme R; le sezioni di Dedekind inoltre permettono di dare una definizione di numero reale, e in particolare di numero irrazionale, del tutto "sganciata" da una eventuale rappresentazione geometrica. Dai tempi di Pitagora fino a Dedekind, infatti, la radice quadrata di 2 era definita come la misura dell'ipotenusa di un triangolo rettangolo isoscele di cateto unitario; invece con Dedekind essa viene definita come il limite cui tendono due sezioni del campo razionale, o meglio, come ha detto Paolo Zellini, « una approssimazione successiva a due limiti tra loro adiacenti della classe inferiore Ap e della classe superiore Bp ». Ad esempio, il numero:
0,1010011000111000011110000011111...
non è passibile di alcuna rappresentazione geometrica, eppure è un numero irrazionale, essendo privo di frazione generatrice. L'unico modo per definirlo dunque è tramite le sezioni di Dedekind.
Esistono anche dei numeri dei quali si ignora ancora oggi se siano razionali o irrazionali. Il caso più famoso è rappresentato dalla cosiddetta costante di Eulero-Mascheroni, molto importante nella Teoria dei Numeri, che può essere così definita:
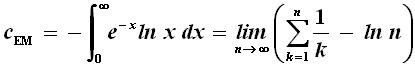
I suoi primi venti decimali sono 0,57721566490153286060..., ma nessuno finora è riuscito a dimostrarne rigorosamente l'irrazionalità. Non possono non venire in mente, a questo proposito, le parole del Qoelet:
« Chi è come il saggio? Chi conosce la spiegazione delle cose? » (Qo 8, 1)

Il Qoelet in una miniatura del
XII secolo,
biblioteca della Badia di
Cava de' Tirreni
Ma se pensate che i paradossi circa l'infinito fossero tutti risolti, vi sbagliate di grosso. A mettere in evidenza alcune antinomie nel cuore profondo dell'infinito matematico fu Georg Cantor (1845–1918), matematico russo naturalizzato tedesco, che fu padre della teoria degli insiemi. Grande filosofo oltre che matematico, i matematici sorti dopo di lui gli devono molto: fu lui a introdurre il concetto fondamentale di "transfinito", che nessun discorso sull'infinito può più ignorare. L'idea dominante fino a Cantor era stata che se l'infinito esiste, allora è unico: è una sorta di "assoluto" kantiano oltre il quale non si può più andare. Cantor invece ebbe il merito di dimostrare che esistono infiniti maggiori e infiniti minori, che lui battezzò appunto "transfiniti".
Tanto per cominciare, egli definì infinito ogni insieme equipotente ad una sua parte propria, cioè che si possa mettere in corrispondenza biunivoca questo suo sottoinsieme. Come abbiamo visto infatti parlando dei paradossi di Galileo, l'insieme dei numeri naturali è equipotente all'insieme dei numeri naturali pari, che di N è un sottoinsieme proprio. Ma questo secondo Cantor non è un arzigogolo mentale: è solo la dimostrazione che l'insieme dei numeri naturali è infinito. Cantor portò un altro efficace esempio a sostegno della sua tesi, quello dell'albergo con un numero infinito di stanze, chimato "albergo di Hilbert". Si tratta di un albergo con un numero infinito numerabile di stanze. Supponiamo che tutte le stanze dell'albergo siano occupate, ma che improvvisamente arrivi un numero indefinito di nuovi clienti a chiedere una camera. Occorre accontentarli, per rispettare il comando divino
« Il Signore, vostro Dio, è il Dio degli dèi, rende giustizia all'orfano e alla vedova, ama il forestiero e gli dà pane e vestito. Amate dunque il forestiero, perché anche voi foste forestieri nella terra d'Egitto. » (Dt 10, 17-19)
«
Il Signore protegge i forestieri,
egli sostiene l'orfano e la vedova,
ma sconvolge le vie dei malvagi. » (Salmo 146, 9)
« Dice il Signore: Praticate il diritto e la giustizia, liberate il derubato dalle mani dell'oppressore, non frodate e non opprimete il forestiero, l'orfano e la vedova, e non spargete sangue innocente in questo luogo. » (Ger 22, 3)
Ebbene, nell'albergo di Hilbert è sempre possibile accogliere nuovi clienti, e addirittura liberare un numero infinito di stanze: basta chiedere a tutti i clienti già alloggiati di spostarsi nelle stanze con un numero doppio di quello che occupano ora. Chi è nella stanza numero 1 si trasferirà dunque nella numero 2, chi occupa la 2 si trasferirà nella 4, chi alloggia nella 3 si sposterà nella 6, e via dicendo. In questo modo tutti avranno una camera a disposizione, essendo il numero delle stanze infinito, e si libereranno tutte le infinite stanze di numero dispari!

Cantor definì potenza o cardinalità di un insieme il numero dei suoi elementi. Come già detto sopra, si definisce numerabile ogni insieme equipotente all'insieme dei numeri naturali N. Cantor definì potenza del numerabile o cardinalità del numerabile tale numero infinito, e lo si indica con la prima lettera dell'alfabeto ebraico, la alef א, cui è aggiunto in apice uno zero, da cui il nome di alef con zero:

L'alef con zero א0 indica un'infinità di elementi, eppure Cantor lo tratta come un vero e proprio numero cardinale. Cantor indicò con א1 la più piccola cardinalità più che numerabile, con א2 la successiva e così via. In questo modo individuò una successione di entità א0, א1, א2 ... che si dicono numeri cardinali transfiniti. Dopo aver definito questa nuova classe di numeri, il nostro matematico dimostrò il Teorema di Cantor: dato un insieme di qualsiasi cardinalità (cioè di un qualsiasi numero di elementi), esiste sempre un insieme di cardinalità maggiore. In particolare, dato un insieme A , l'insieme delle parti P(A), cioè l'insieme formato da tutti i possibili sottoinsiemi di A, ha sempre cardinalità maggiore di quella di A. Il teorema di Cantor è ovvio per insiemi finiti, dato che l'insieme delle parti di un insieme con n elementi è formato da 2n elementi; ma è valido anche per insiemi infiniti, e ci dice che l'insieme delle parti di un insieme numerabile è più che numerabile: א(P(N)) > א0. Naturalmente l'insieme delle parti di P(N), cioè P(P(N)), avrà cardinalità maggiore di P(N), e così via; anche i numeri cardinali transfiniti dunque sono infiniti.
Dimostriamo ora che l'insieme dei numeri razionali assoluti è un insieme numerabile, cioè ha la potenza א0. I numeri razionali possono essere tutti scritti sotto forma di frazione. Disponiamoli allora in una matrice di dimensione infinita che ha in ogni riga il valore del numeratore, e in ogni colonna quello del denominatore, in questo modo:

In questo modo vengono scritti tutti i numeri razionali assoluti, eventualmente anche con delle ripetizioni (ad es. 2/4 e 1/2 rappresentano lo stesso numero razionale). Seguiamo ora il percorso indicato dalle frecce nella figura, che procedono in senso diagonale: partiamo da 1/1, scendiamo di un posto a 2/1, risaliamo a 1/2 lungo la diagonale, spostiamoci a destra di un posto in 1/3, scendiamo in senso inverso lungo la diagonale attraversando 2/2 e 3/1, scendiamo di un posto a 4/1, risaliamo lungo la diagonale attraversando 3/2, 2/3 e 1/4, e così via. In tal modo abbiamo dimostrato che è possibile disporre in un'unica riga i numeri razionali assoluti, e metterli in corrispondenza biunivoca con i numeri naturali:

La stessa dimostrazione può essere ripetuta per l'insieme dei numeri razionali relativi. Di conseguenza gli insiemi N e Q hanno la stessa cardinalità!
Facciamo ora un altro esempio di insiemi in corrispondenza biunivoca tra loro, cioè che hanno la stessa cardinalità. Dimostriamo che i punti del segmento ( 0 ; 1 ) possono essere messi in corrispondenza biunivoca con quelli dell'intera retta reale, cioè che i punti di AB sono "tanti quanti" quelli dell'intera retta cui essa appartiene. Allo scopo, consideriamo una semicirconferenza aperta (senza i punti estremi) A'B' il cui diametro ha lunghezza pari ad AB, e mostriamo che i suoi punti possono essere messi in corrispondenza biunivoca con quelli di una retta r ad essa tangente nel suo punto medio H. Consideriamo il segmento AB ottenuto proiettando su r il diametro A'B' della semicirconferenza, in modo che H sia il suo punto medio. Ad ogni punto P del segmento AB corrisponde un punto Q della semicirconferenza A'B', ottenuto proiettando P perpendicolarmente ad r sulla semicirconferenza A'B', e a questo punto Q corrisponde un punto P' della retta r, ottenuto proiettando Q su r con una semiretta uscente dal centro O della semicirconferenza; viceversa, con procedimento analogo, ad ogni punto P' della retta corrisponde un punto Q della semicirconferenza e un punto P del segmento AB, come mostra questa figura:
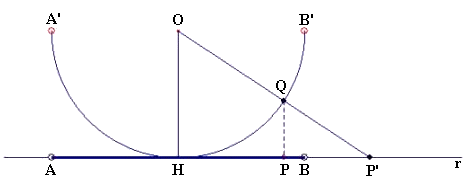
In definitiva, quindi, ogni intervallo aperto può essere messo in corrispondenza biunivoca con l'insieme dei punti di una retta, e i punti di una retta sono "tanti quanti" i punti di un intervallo aperto. Nella figura seguente tale corrispondenza viene illustrata in modo grafico:

Tale corrispondenza, scelto un opportuno sistema di assi cartesiani ortogonali, può essere espressa anche in modo analitico; lascio quest'esercizio ai lettori volenterosi ed esperti. Abbiamo così ritrovato una diversa versione del paradosso di Galileo, secondo il quale la parte può essere uguale al tutto, se l'insieme è infinito!
Il passo successivo consiste nel chiedersi che i numeri reali possono o meno essere messi in corrispondenza biunivoca con i numeri naturali. La risposta è negativa, e la dimostrazione può essere eseguita per assurdo. Supponiamo che i numeri reali compresi nell'intervallo ( 0 ; 1 ) formino un insieme numerabile. In questo caso sarà possibile scriverli in un elenco numerabile come quello sopra realizzato, in cui ciascun numero reale compreso tra 0 e 1 sarà contrassegnato da un numero naturale n. Il primo numero reale dell'intervallo, si potrà scrivere come:
0, a1 a2 a3 a4 a5 a6 …
dove a1, a2, a3, a4, a5, a6 … sono le sue cifre decimali dopo la virgola. Costruiamo ora, seguendo il procedimento di Cantor, un nuovo numero reale compreso tra 0 ed 1, che non è elencato nella figura seguente.

Il numero ha come prima cifra 0. Al primo posto dopo la virgola si sceglie una cifra diversa da a1, al secondo posto si sceglie una cifra diversa da b2, al terzo posto si sceglie una cifra diversa da c3, e così via. Con questo procedimento viene costruito un numero reale compreso tra 0 e 1, che però è diverso da tutti quelli dell'elenco precedente, contro l'ipotesi che l'elenco indicasse tutti i numeri compresi tra 0 e 1. Siamo arrivati ad un assurdo, e pertanto l'insieme dei numeri reali dell'intervallo ( 0, 1 ) non è numerabile. Come scrisse lo stesso Cantor, « questa dimostrazione appare degna di nota non solo a causa della sua grande semplicità, ma specialmente perché il principio in essa seguito si lascia senz'altro estendere al teorema generale, che le potenze di insiemi ben definiti non abbia alcun massimo, ossia, il che è lo stesso, che ad ogni insieme dato L può essere associato un altro insieme M di potenza maggiore di L »: per l'appunto, il suddetto Teorema di Cantor.
Ne consegue che l'insieme dei numeri reali non può essere posto in corrispondenza biunivoca con i numeri naturali; la cardinalità dei numeri reali è quindi maggiore della cardinalità del numerabile. La cardinalità dei numeri reali si chiama potenza del continuo, o cardinalità del continuo, e si indica con la lettera c. Ne consegue che molti insiemi che sembrano più grandi dei numeri naturali siano in realtà numerabili, ma non ogni insieme infinito è numerabile: dimostrando quest'ultima affermazione il 12 dicembre 1873, Cantor fece compiere un passo avanti da gigante al pensiero matematico riguardante l'infinito, che si scopre sempre accrescibile e mai assoluto. A questo punto, però, spunta un dilemma: tra la cardinalità dei razionali e quella dei reali esiste una cardinalità intermedia? Cantor ipotizzò anche, ma non riuscì a dimostrarlo, che il continuo è la potenza immediatamente successiva al numerabile, cioè che c = א1. In altre parole, non c'è alcun cardinale intermedio tra א0 e א1, tra la cardinalità del numerabile e quella del continuo. Questa è nota come "ipotesi del continuo".
Una delle più importanti scoperte effettuate da Cantor è però la seguente: tutti i punti del piano e dello spazio sono "tanti quanti" quelli di una retta. A proposito di tale assunto, lo stesso Cantor, in una lettera a Dedekind del 1877 scrisse: « Lo vedo, ma non ci credo! » In effetti l'enunciato è alquanto sorprendente, perché afferma la possibilità di costruire una corrispondenza biunivoca tra i punti di una retta e i punti del piano. Consideriamo allo scopo l'intervallo aperto ( 0, 1 ) e mostriamo come esso può essere messo in corrispondenza biunivoca con il quadrato aperto di lato unitario e di vertici O (0 ; 0), A (1 ; 0), B (1 ; 1) e C (0 ; 1)., in un opportuno sistema di riferimento cartesiano ortogonale.
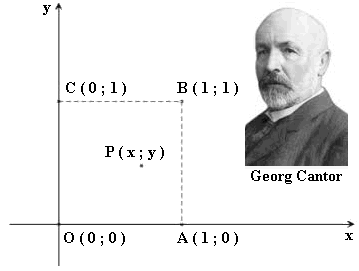
Un punto P del quadrato avrà coordinate ( x ; y ), dove x e y sono numeri reali compresi tra 0 e 1 e possono essere scritti in forma decimale:
x =
0, a1 a2 a3 a4 a5 a6
...
y = 0, b1 b2 b3 b4 b5 b6
...
dove ai e bi sono cifre comprese tra 0 e 9 (ad esempio 0,539236...). Alla coppia ordinata ( x ; y ), che identifica univocamente il punto P, si può far corrispondere il numero reale compreso tra 0 e 1 così costruito:
c = 0, a1 b1 a2 b2 a3 b3 ...
che identifica univocamente l'ascissa di un punto del lato del quadrato OABC. Viceversa ad un qualunque punto del lato OA cui corrisponde univocamente il numero decimale:
c = 0, c1 c2 c3 c4 c5 c6 ...
si può far corrispondere la coppia ordinata formata da x = 0, c1 c3 c5 ... e y = 0, c2 c4 c6 ..., che individua un punto del quadrato. La corrispondenza biunivoca tra punti del quadrato e punti di un suo lato è così costruita, e l'affermazione iniziale è pertanto dimostrata. Questo ragionamento ci insegna a tenere ben distinti i concetti di cardinalità e di dimensione: un quadrato ha dimensione due, un suo lato ha dimensione uno, eppure i punti del quadrato sono tanti quanti i punti di un suo lato. La corrispondenza ora costruita, tuttavia, sfugge alla nostra intuizione perché non è facilmente visualizzabile con gli occhi della nostra mente.
Per convincersi della possibilità di mettere in corrispondenza i punti di una retta ed i punti del piano si possono utilizzare delle curve particolari, che generalizzano il procedimento usato per dimostrare che Q è equipotente ad N, come la curva di Peano, dal nome del matematico piemontese Giuseppe Peano (1858-1932) che la ideò nel 1890, la quale progressivamente riempie il quadrato OABC, come si vede nella figura seguente:

La curva di Peano non è derivabile in alcun punto, e oggi sappiamo che essa rappresenta storicamente uno dei primi esempi mai ideati di frattale.
Non possiamo chiudere questa discussione sull'infinito senza citare altri paradossi e antinomie scoperte in quest'ambito dopo il lavoro di Cantor. I due termini citati non sono sinonimi, contrariamente a quanto credono molti: Lucio Lombardo Radice nel suo saggio "L'infinito" (1981) definì il paradosso un'affermazione incredibile, contraria all'opinione corrente ed intuitiva, e l'antinomia (dal greco "contraddizione") come un'affermazione che nell'ambito di una certa teoria è possibile dimostrare come vera, e tale che contemporaneamente si possa dimostrare anche la sua negazione. Quello di Zenone e della tartaruga è un evidente paradosso, perchè esso cerca di dimostrare (partendo da basi che oggi sappiamo errate) che la tartaruga non può essere superata da un corridore più veloce di lei. Circa le antinomie, invece, non è possibile trovare un errore nel ragionamento alla base di essa, perchè esse sono conseguenza dell'incompletezza stessa della teoria presa in considerazione.
Nel nostro caso, le antinomie riguardano la teoria degli insiemi, che Cantor e i suoi seguaci hanno posto all'origine stessa della matematica come noi la conosciamo; per questo tali antinomie hanno fatto parlare di crisi dei fondamenti della matematica tradizionale. La più famosa di queste antinomie è quella formulata nel 1903 da Bertrand Russell (1872-1970), che fece sorgere seri dubbi sulla coerenza interna della teoria degli insiemi sviluppata da Cantor. L'antinomia di Russell può essere così sintetizzata. Alcuni insiemi sono elementi di se stessi, altri non lo sono: l'insieme di tutti gli insiemi con più di 10 elementi è elemento di se stesso, mentre l'insieme di tutti i libri non è elemento di se stesso, non essendo un libro. Consideriamo ora l'insieme X di tutti gli insiemi che non sono elementi di se stessi. Se X appartiene a sé stesso, X soddisfa la definizione da noi data, quindi è uno degli "insiemi che non appartengono a sé stessi"; ma allora X non appartiene a sé stesso, il che contraddice il nostro enunciato. Se invece X non appartiene a sé stesso, non soddisfa la definizione; quindi X non è uno degli "insiemi che non appartengono a sé stessi". Ma allora X è un insieme che appartiene a sé stesso, il che contraddice il primo enunciato.
Come si vede, alla base di questa antinomia non c'è un ragionamento sottilmente sbagliato, ma l'ipotesi fondamentale alla base dell'aritmetica stessa, e che uno dei più grandi studiosi di logica dell'età moderna, il tedesco Friedric Ludwig Gottlob Frege (1848-1925), aveva così enunciato nei suoi "Die Grundlagen der Arithmetik" ("I fondamenti dell'aritmetica") del 1884: ogni proprietà definisce l'insieme degli elementi che la verificano, cioè la sua estensione. L'antinomia russelliana in particolare verte sull'uso del concetto di "estensione" di una certa proprietà, e venne accolta con costernazione dai matematici del tempo.
Non meno devastante, per i fondamenti della matematica, è un'altra antinomia nota come antinomia di Cantor o della classe totale. Si consideri la totalità degli insiemi, chiamata da Cantor la "classe totale" A, che potremo chiamare l'insieme di tutti gli insiemi. Sia P(A) l'insieme delle parti di A. Per quanto precedentemente visto, P(A) dovrebbe avere cardinalità maggiore di A, ma essendo A l'insieme di tutti gli insiemi, esso contiene P(A) come suo elemento, quindi P(A) dovrebbe avere cardinalità non maggiore di A.
Queste antinomie scossero il mondo matematico all'alba del XX secolo e determinarono la nascita di diverse scuole epistemologiche circa la natura medesima della Matematica. Gli Intuizionisti, uno dei cui maggiori esponenti fu l'olandese Luitzen Egbertus Jan Brouwer (1881-1966), accettarono come vero esclusivamente il Postulato Ristretto della Matematica, cioè l'esistenza della successione infinita dei numeri naturali e tutto ciò che da essa conseguiva; rifiutarono il Principio del Terzo Escluso affermando che una proposizione può essere né vera né falsa, cioè indecidibile e, conseguentemente, negarono valore alle dimostrazioni per assurdo: affermare perciò che esiste un oggetto dotato di certe proprietà significa che c'è un metodo riconosciuto che permette di trovare o di costruire tale oggetto mediante un numero finito di passi.
Il famoso David Hilbert avviò invece la scuola di pensiero dei Formalisti, i quali partirono dall'idea che esistenza in Matematica significa coerenza, cioè non contraddizione, e poiché la coerenza delle teorie più complesse si riconduceva alla coerenza dell'aritmetica, concentrarono i loro sforzi nel tentativo di formalizzare completamente l'aritmetica. Alcuni svilupparono tale posizione fino alle estreme conseguenze, giungendo alla conclusione che la Matematica non è altro che un gioco le cui pedine sono contrassegni privi di significato secondo delle regole formali concordate in partenza.
Infine i Logicisti, un esponente di rilievo dei quali fu Bertrand Russell, tentarono di formalizzare la Matematica con la Logica: essi affermavano che i numeri interi sono sufficienti a descrivere i risultati dell'Analisi, ma essi sono stati a loro volta descritti nella Logica Simbolica di Peano la quale fornisce, a loro giudizio, un tessuto logico primario che sembra avvalorare dall'esterno (al di fuori della Matematica) la Matematica stessa.

Charlie Brown alle prese con l'infinito
Nel 1931 tuttavia l'austriaco Kurt Gödel (1906-1978) infranse i sogni dei Formalisti che speravano di costruire un sistema formale completo, dimostrando a soli 25 anni che all'interno di qualunque sistema formale esistono certe asserzioni ben precise che non possono essere né dimostrate, né invalidate nell'ambito degli assiomi del sistema considerato; perciò, usando i metodi convenzionali, non si può essere certi che gli assiomi dell'aritmetica non portino a contraddizioni. È questo il celeberrimo Teorema di Incompletezza. Nel 1938 poi Kurt Gödel dimostrò che non si poteva dimostrare che l'Ipotesi del Continuo di Cantor fosse falsa rimanendo nel quadro della teoria assiomatica degli insiemi formulata da Ernst Zermelo (1871-1953) e Abraham A. Fränkel (1891-1965). Si può supporre insomma che non esista un cardinale transfinito intermedio tra il numerabile e il continuo, come si può supporre il contrario, e questa supposizione non creerà contraddizioni. Nel 1963, poi, l'americano Paul Joseph Cohen (1934-2007) dimostrò che non si poteva provare che l'ipotesi del continuo fosse vera neppure nel quadro della teoria degli insiemi, e costruì un sistema formale che verifica tutti gli assiomi "ordinari" ma nel quale l'Ipotesi del Continuo di Cantor è rifiutata, dimostrando così che è possibile costruire tanto una "Matematica Cantoriana" quanto una "Matematica Non Cantoriana", analogamente a quanto era avvenuto in Geometria un secolo prima con la nascita delle Geometrie non euclidee, che non contemplano tra i loro assiomi il celebre Quinto Postulato di Euclide. Nasce così il Metodo Assiomatico moderno, che non è soltanto deduttivo (si assumono come verità primitive evidenti alcune proprietà fondamentali, chiamate "postulati" o "assiomi", dalle quali si deducono nuove proprietà), ma è ipotetico-deduttivo: gli assiomi non sono più verità primitive indimostrabili, ma semplici ipotesi relative ad enti del pensiero non definiti, e perciò, se si considerano enti concreti che verificano le proprietà espresse dagli assiomi, allora valgono anche le proprietà espresse dai teoremi dedotti da questi per via strettamente logica. Ad ogni interpretazione degli enti primitivi corrisponde un modello concreto della teoria assiomatica, di per sé astratta, formale.
L'assunzione del Metodo Assiomatico moderno comporta insomma la perdita dell'unità; in altre parole, non esiste più la Matematica, ma esistono le Matematiche, così come non c'è più la Geometria (intesa come Euclidea, l'unica un tempo considerata ammissibile), ma le Geometrie, che oggi sappiamo essere alla base di complessi rami della Fisica Moderna, come la Relatività Generale di Einstein (1915). Questo d'altro canto apre nuovi vastissimi campi di ricerca e quindi nuove prospettive di progresso sia del pensiero matematico che, conseguentemente, del pensiero scientifico e del pensiero umano in generale. Su tutte queste ingegnose dispute e dimostrazioni riguardanti l'infinito pesano però come macigni le parole di Albert Einstein:
« Solo due cose sono infinite, l'universo e la stupidità umana, e non sono sicuro della prima. »
![]()