![]()
|
"Qual è il geometra che tutto s'affige Dante, Paradiso XXXIII, 133-135 |
.
6.1 Le forze apparenti
Ancora all'inizio del XX secolo si pensava che lo spazio ed il tempo fossero realtà assolute, cioè che ogni evento fosse univocamente individuato da tre coordinate spaziali ed una temporale. Questa certezza andò in crisi con la scoperta che la luce ha sempre la stessa velocità dal punto di vista di qualsiasi osservatore, immobile o in movimento che sia, come avevano dimostrato Albert Abraham Michelson (1852–1931) ed Edward Williams Morley (1838–1923) con il loro famoso esperimento del 1887. Proprio a partire da questo postulato, Albert Einstein (1879-1955) con il famoso articolo "Zur Elektrodynamik bewegter Körper" ("Sull'Elettrodinamica dei Corpi in Movimento") del 1905 propose la sua Teoria della Relatività Ristretta. Per chi vuole saperne di più rimando al mio ipertesto "Il Treno di Einstein" dedicato interamente a tale teoria. Qui basti ricordare che essa ruota intorno a un concetto rivoluzionario: spazio e tempo sono concetti relativi al sistema di riferimento, mentre ad essere costante è la velocità della luce c.
Se ne deduce che nessuna informazione può viaggiare più veloce della luce. Invece, come abbiamo visto, secondo la teoria di Newton la forza di gravità ha effetto istantaneo: se il Sole si dovesse spostare dalla propria posizione, la forza che esso esercita sulla Terra cambierebbe immediatamente, senza alcun ritardo. L'informazione relativa al movimento del Sole si trasmetterebbe quindi istantaneamente, cioè a velocità maggiore di c. Inoltre, mentre nella Fisica Classica vale il cosiddetto Principio di Relatività Galileiana, che segue le ben note Trasformazioni di Galileo, nella nuova Relatività di Einstein valgono al contrario le Trasformazioni di Lorentz, più complicate, che si trasformano in quelle di Galileo solo se v << c. Orbene, tramite calcoli opportuni è facile verificare che la legge di Gravitazione Universale non è invariante rispetto alle Trasformazioni di Lorentz: la forza di gravità non rispetta quindi i fondamenti della Relatività Galileiana, e la Gravitazione Universale risulta incompatibile con le scoperte di Einstein.
Tutto questo fa sentire l'esigenza di una nuova Teoria della Gravitazione, che superi e completi quella di Newton. Einstein si dedicò ad essa con passione subito dopo la pubblicazione della sua Relatività Ristretta, ma il problema era così complesso, che egli impiegò anni ed anni per elaborare una teoria coerente, che si rivelò genialissima. Siccome la Relatività Ristretta si occupa di sistemi inerziali, che si muovono cioè l'uno rispetto all'altro di moto rettilineo uniforme, il genio di Ulm cominciò a domandarsi che cosa accade nei sistemi che si muovono l'uno rispetto all'altro di moto accelerato.
Allo scopo, si consideri un vagone ferroviario chiuso, con al suo interno un pendolo, un secchio d'acqua e alcuni oggetti non vincolati:
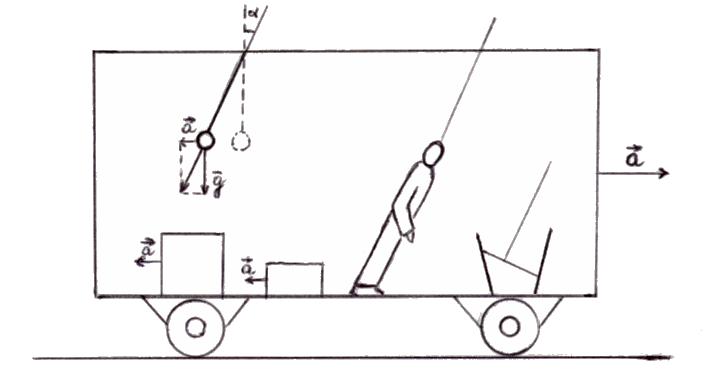
Fino a che il vagone si muove di moto uniforme, pare che esso rimanga fermo a un osservatore chiuso dentro il vagone: egli osserverà il pendolo in posizione assolutamente verticale, il pelo dell'acqua sarà perfettamente orizzontale, e gli oggetti saranno immobili. Se questo però prende ad accelerare con accelerazione a, accadranno effetti strani. Per un osservatore solidale con la terra, nel sistema di riferimento K, i corpi tenderanno a mantenere per inerzia la propria posizione, e "rimarranno indietro". Ma per l'osservatore chiuso nel vagone, nel sistema K' solidale con esso, essi saranno soggetti ad un'accelerazione a inspiegabile. Il pendolo si sposterà dalla posizione di equilibrio nello stesso verso del moto dei corpi. Infatti é soggetto all'accelerazione a, che si compone con la gravità g facendo inclinare il pendolo di un angolo α tale che:
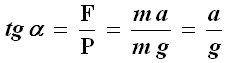
Ogni retta inclinata sul pavimento di un angolo α può essere considerata la verticale propria del sistema accelerato K', perché l'osservatore in K' starà in perfetto equilibrio formando un angolo α con il pavimento, e anche l'acqua del secchio si inclinerà formando una superficie la cui normale coincide con la verticale propria. L'osservatore attribuirà questa accelerazione a ad una forza F = m a, che in realtà non esiste rispetto all'osservatore solidale con la terra. Per questo tale forza è detta forza apparente.
Si consideri ora invece un disco in rotazione con velocità angolare uniforme ω:
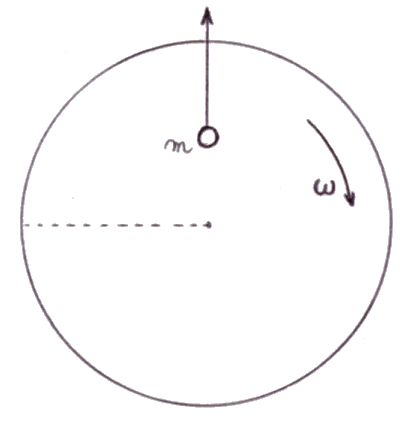
Un corpo non vincolato posto su di esso é soggetto, per l'osservatore solidale con la terra in K, ad una accelerazione centrifuga a = ω2 r, tale che il corpo si allontani dall'asse del disco. Invece, per un osservatore solidale con il disco nel sistema K', questo non é in moto circolare intorno all'asse, però é ugualmente soggetto ad una forza, che non é apparente perché sussiste in K (é dovuta alla rotazione del corpo insieme al disco), ma che non risulta in nessuna maniera giustificabile.
Se sul disco fosse posto un secchio che ha l'asse coincidente con il suo perno, come si vede nel sottostante disegno di Enrica Soldavini, la forza centrifuga si comporrebbe con la gravità, e l'acqua assumerebbe una superficie di tipo parabolico: la componente orizzontale a cresce in funzione della distanza dall'asse , quella verticale g cresce in funzione del quadrato dell'altezza sul disco. La loro risultante é la normale alla superficie del liquido in ogni punto.

Altro esempio di forza apparente é la forza di Coriolis, consistente in una forza che agisce perpendicolarmente al moto dei corpi un corpo quando si osserva il suo moto in un sistema di riferimento K' che sia in moto circolare rispetto a un sistema di riferimento inerziale K. La sua intensità é data dalla legge di Ferrel:
![]()
dove v é la velocità del corpo, ω la velocità angolare di K', ρ la densità del mezzo in cui si muove, φ la latitudine a cui il corpo si trova. Essa deve il suo nome all'ingegnere francese Gaspard-Gustave de Coriolis (1792–1843), che per primo la descrisse nel 1835. La forza di Coriolis ha un ruolo importante nella dinamica atmosferica e nella meteorologia, poiché spiega il moto dei venti, la formazione e la rotazione delle tempeste e la direzione delle correnti oceaniche. Ad esempio, i venti che scorrerebbero verticalmente dai poli verso l'equatore se la Terra fosse ferma, sono invece deviati dalla forza di Coriolis, dand vita a venti costanti noti come alisei, che nell'emisfero boreale soffiano da nord-est verso sud-ovest, e nell'emisfero australe da sud-est verso nord-ovest. Sempre alla forza di Coriolis è da ascrivere l'effetto Eötvös, per il quale, indipendentemente dall'emisfero nel quale si trovano, gli oggetti in moto da ovest verso est subiscono una forza diretta verso l'alto che li fa sembrare più leggeri, mentre quelli in moto in direzione opposta subiscono una forza diretta verso il basso e appaiono più pesanti (tale effetto è comunque troppo piccolo rispetto alle altre forze in gioco per essere significativo nei fenomeni dinamici).
.
6.2 Il principio di Mach
Ma che senso hanno le forze apparenti? Rispetto a quale sistema esse agiscono? La risposta più ovvia sarebbe: rispetto al sistema in cui esse si manifestano. Ma ha senso una risposta simile? Nel caso del secchio che ruota, la forza non si manifesta rispetto al contenitore, perché nello stesso K' esso appare fermo. Isaac Newton sostenne allora l'esistenza di uno spazio assoluto, che si può considerare immobile rispetto a tutti i punti dell'universo, e portò a suo sostegno l'argomentazione che le forze apparenti sono il risultato di un'accelerazione rispetto allo spazio assoluto.
Ernst Mach (1838–1916) invece rigettò l'idea dello spazio assoluto come "metafisico", e sostenne l'ipotesi per cui le forze apparenti sono determinate da interazioni con la materia circostante. Noi siamo circondati da ogni parte da materia stellare, quindi le forze apparenti vanno riferite al sistema delle "stelle fisse", cioè a tutto il resto della materia universale, al "tutto". Questo concetto è noto con il nome di principio di Mach. Ogni corpo possiede un'inerzia, quindi una massa, che si oppone al moto; dunque le forze apparenti vanno considerate, secondo Mach, come la resistenza opposta da un corpo al "trascinamento" rispetto alle stelle fisse. É evidente che, se le forze apparenti risultano dall'interazione di due corpi, esse si devono manifestare sia nel caso del moto relativo del primo verso il secondo, sia nel caso del moto relativo del secondo verso il primo. Mach si spinse perciò ad affermare che l'esperienza del secchio sopra descritta sarebbe stata probante solo se si fosse provato a tenere fermo il secchio e a far ruotare intorno ad esso le stelle fisse! Approfondiremo meglio questo complicato concetto nel § 7.8.
.
6.3 Il principio di equivalenza
Einstein si valse delle ricerche di Mach per elaborare la sua teoria gravitazionale, e partì nel 1908 formulando il cosiddetto Principio di Equivalenza. Consideriamo un laboratorio in cui alcuni sperimentatori compiono delle ricerche sull'accelerazione di gravità. Se essi osservano che tutti i corpi cadono con la stessa accelerazione in una certa direzione, concluderanno che il loro laboratorio è immerso in un campo gravitazionale in piccolo. Questa però non è l'unica spiegazione possibile.
Si supponga infatti che il laboratorio in questione sia posto dentro un'astronave o una stazione spaziale (come la celeberrima Babylon 5 della fantascienza) posta nello spazio lontanissimo da ogni pianeta. Se chi occupa l'astronave dispone di un tavolo da biliardo e di un pendolo, e vede le palle da biliardo rotolare verso un lato del tappeto verde, e il pendolo inclinarsi da quella parte, può concludere che dietro la sua aeronave è comparso un pianeta che ha attratto palle e pendolo, Ma ne è proprio sicuro? Come si vede dalla figura in basso, può darsi benissimo che non ci sia alcun pianeta, ma che l'astronave, precedentemente in moto con velocità costante, ora abbia acquisito un'accelerazione a esattamente pari al campo gravitazionale dell'ipotetico pianeta! Insomma, dentro la navicella sembrerà agli astronauti di muoversi come se il razzo fosse ancora sulla rampa di lancio.

Se invece il razzo, prima in moto uniforme, decelerasse all'improvviso, gli astronauti si sentirebbero proiettati in avanti, come se un misterioso pianeta si fosse parato davanti al razzo, facendo risentire gli effetti della propria gravitazione. Siccome il campo gravitazionale ha le stesse dimensioni fisiche di un'accelerazione, non vi è alcun modo, compiendo esperimenti di dinamica, per decidere se è improvvisamente comparso un pianeta, o se l'astronave ha cominciato ad accelerare verso destra. L'unico modo per riuscirci sarebbe quello di... guardare fuori dall'astronave.
Tutto ciò condusse Einstein a formulare il Principio di Equivalenza:
Un sistema accelerato é perfettamente equivalente ad un sistema immerso in un campo gravitazionale.
Esso costituisce il punto di partenza di quell'importantissima teoria oggi conosciuta come RELATIVITÀ GENERALE, così detta perché quella ristretta ne é in effetti un caso particolare, qualora sia a = 0, e i moti non siano accelerati, ma rettilinei uniformi. Il genio di Ulm elaborò questa teoria nel suo saggio "Die Grundlage der allgemeinen Relativitätstheorie" (Fondamenti di Relatività Generale") del 20 marzo 1916 (ne ricorre dunque quest'anno il centesimo anniversario):

Il fondamento di tale principio, com'è facile intuire, sta nell'identità tra massa inerziale e massa gravitazionale, del quale abbiamo parlato già nel § 2.8, ed esso ha come importantissime conseguenze l'unificazione tra forze gravitazionali e forze apparenti, e la necessità di modificare lo stesso concetto di "spazio fisico" così come esso è implicato dalla geometria euclidea e dalla fisica newtoniana.
Prima di affrontare questo argomento, però, ne approfitto per farvi notare un'altra basilare conseguenza del Principio di Equivalenza: l'effetto di un campo gravitazionale può essere annullato da un campo di accelerazioni. Basta infatti che il vettore di campo gravitazionale g sia esattamente uguale ed opposto all'accelerazione del campo:
![]()
Pensiamo infatti alla cabina di un ascensore in caduta libera perché si è rotto il cavo: essa precipita verso il basso con accelerazione esattamente pari a g, e tutti i corpi al suo interno si trovano soggetti ad una forza apparente m a = m g diretta verso l'alto, che annulla esattamente la forza peso diretta verso il basso. Per questo i corpi all'interno di tale cabina appaiono privi di peso! Se al contrario la cabina accelerasse verso l'alto con accelerazione pari a g, questa si sommerebbe all'accelerazione gravitazionale, e i corpi parrebbero raddoppiare il proprio peso!
Questo Principio ci aiuta anche a comprendere perchè gli oggetti volteggiano, all'interno della International Space Station, quando la TV trasmette immagini degli astronavi ripresi a bordo di esse, come si vede nel video qui sopra. "Perchè dentro di essa vi è assenza di gravità", mi risponderete voi. Ma si tratta di una risposta ingenua: se la gravità terrestre fosse zero, non potrebbe trattenere la ISS in orbita intorno al nostro pianeta! La soluzione di questo apparente paradosso sta proprio nella formula appena scritta: il campo di accelerazione centrifuga dovuto al moto della ISS intorno alla Terra è sufficiente per annullare in ogni punto il campo gravitazionale dovuto all'attrazione terrestre, proprio come avviene nel suddetto ascensore!
.
6.4 Deflessione della luce
Il Principio di Equivalenza ha una conseguenza assolutamente inaspettata, ed estranea a quella che noi chiamiamo Fisica Classica. Supponiamo di trovarci in un razzo che si muove con accelerazione elevata, e di avere un fascio di luce che attraversi più schermi fluorescenti, posti a distanza costante d , così da lasciare su di essi una traccia visibile (il disegno è di Enrica Soldavini):
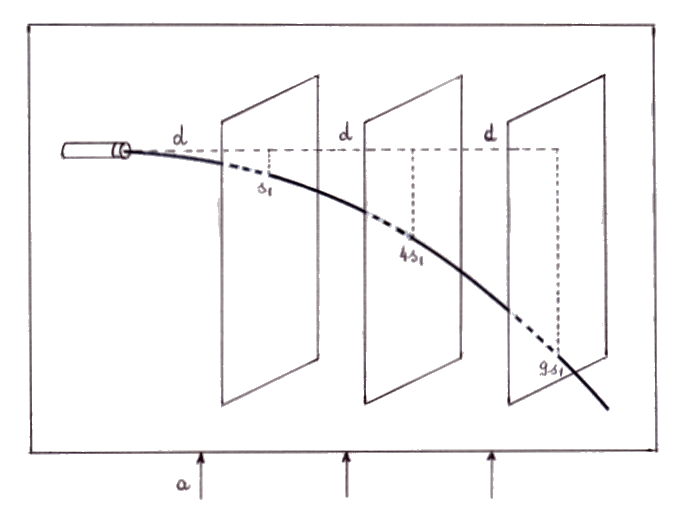
Gli intervalli di tempo che vanno dall'emissione del raggio luminoso al momento in cui esso lascia la traccia sul primo, sul secondo,.....schermo misurano rispettivamente:
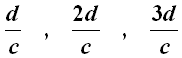 e così via.
e così via.
Ma, durante ciascuno di questi intervalli, il razzo si é mosso perpendicolarmente al raggio con accelerazione a, compiendo tragitti pari rispettivamente a:
 ecc.
ecc.
osserviamo che essi possono essere così riscritti:

e così via.
Il moto del raggio di luce, composto di un moto in progressione aritmetica (con legge lineare) e di un moto in progressione geometrica (con legge quadratica), é dunque parabolico! Il campo di accelerazioni ha deflesso il raggio di luce lungo la stessa traiettoria di una palla di cannone!
Orbene, per il Principio di Equivalenza, ciò deve essere vero anche in un sistema gravitazionale. In altre parole, anche la gravità deve essere in grado di deflettere un raggio di luce, altrimenti io avrei trovato un modo per distinguere un campo di gravità da uno di accelerazioni, ed avrei distrutto il Principio. La luce dunque cade in un campo gravitazionale!
Però l'esperienza non sembra poterci venire in aiuto per confermare una simile intuizione: in un secondo un raggio di luce percorre 300.000 chilometri, mentre un corpo qualsiasi cade sulla terra di soli 4,9 metri: appena un sessanta milionesimo! Nessuna speranza, dunque, di osservare i fari della nostra automobile "cadere" verso il suolo per effetto della gravità terrestre, così come non vi è speranza di vedere i fari dell'automobile di Paperino deflessi dalle urla di zio Paperone, come illustrato nella seguente vignetta:

| Vignetta di Giorgio Cavazzano tratta da « Zio Paperone e l'invasione dei Ki-Kongi », sul Topolino n° 394 e 295 del 21 e 28 ottobre 1973 |
Tuttavia, se il campo gravitazionale é molto più forte di quello terrestre e le distanze considerate sono grandi, su scala astronomica, il fenomeno potrebbe diventare rilevabile. Per esempio, un raggio di luce che passi accanto al Sole potrebbe venire deflesso da esso in maniera sensibile. Di quanto? Nel § 2.6 abbiamo calcolato che la stella a noi più vicina ha un'accelerazione di gravità di circa 274 m s-2. Supponiamo che essa agisca, mantenendosi costante, per una distanza dell'ordine del raggio del sole, che sappiamo valere RS = 696.000 Km circa. Il tempo t impiegato dalla luce a percorrere il diametro solare vale:
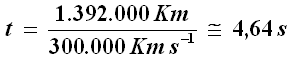
Perciò la "caduta" della luce nel campo di gravità del Sole vale:

L'ordine di grandezza dell'angolo di deflessione é valutabile come rapporto tra questa deflessione ed il raggio solare:
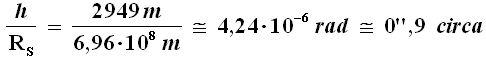
La curvatura dei raggi di luce da parte di grandi masse fu dimostrata sperimentalmente per la prima volta dal fisico britannico sir Arthur Eddington (1882-1944), dell'Università di Cambridge, e la cosa di per sé è stupefacente, perché nel 1915, anno in cui il tedesco Albert Einstein presentò all'Accademia Prussiana delle Scienze la Teoria della Relatività Generale, l'Impero Tedesco e il Regno Unito erano impegnati nella Prima Guerra Mondiale, e la guerra, si sa, non facilita lo scambio di informazioni scientifiche. Pubblicata in tedesco, su una rivista tedesca, infatti, la nuova teoria della gravità non trovò inizialmente una grande diffusione, né fra gli scienziati né fra il pubblico. Fortuna volle che i Paesi Bassi fossero rimasti neutrali durante la Grande Guerra, e all'Università di Leida, prestigiosa istituzione olandese, era professore Willem de Sitter (1872-1934), divenuto più tardi noto per i suoi studi di cosmologia proprio grazie all'applicazione della teoria della Relatività Generale. Arrivatagli notizia della teoria di Einstein, de Sitter ne comprese presto l'importanza e decise di divulgarne i contenuti principali scrivendo alcuni articoli in lingua inglese. In Inghilterra la Relatività Generale trovò subito un sostenitore entusiasta, Arthur Eddington appunto. Nel 1918, nonostante la Grande Guerra fosse ancora in corso, egli riuscì a farsi finanziare dalla Royal Society e dalla Royal Astronomical Society una costosa missione scientifica consistente in una spedizione sull'isola di Principe, nel Golfo di Guinea, per studiare un'eclisse di Sole del 29 maggio 1919, visibile dall'Africa Centrale e totale, l'unica condizione per poter osservare le stelle in vicinanza del Sole, essendo quest'ultimo completamente oscurato dal disco lunare. L'idea era di misurare le posizioni apparenti di alcune stelle di sfondo in prossimità del disco solare occultato dalla Luna e di confrontarle con le rispettive posizioni assunte a distanza di alcuni mesi, quando quelle stesse stelle si trovavano angolarmente più distanti dal Sole e potevano pertanto essere osservate di notte. Per di più l'eclisse di Sole in questione si verificava in condizioni particolarmente favorevoli da questo punto di vista: il campo stellare da osservare era quello dell'ammasso delle Iadi, nella costellazione del Toro, composto da stelle piuttosto luminose e facilmente riconoscibili. Per tutelarsi da eventuali problemi meteorologici, furono organizzate due spedizioni scientifiche in due località toccate dalla fascia di totalità dell'eclisse, che avrebbe attraversato l'Oceano Atlantico dal Brasile all'Africa occidentale: l'astronomo Andrew Crommelin (1865-1939), dell'Osservatorio di Greenwich, si portò a Sobral, nel nord del Brasile, per osservare il Sole eclissato. Il giorno dell'eclisse (ne è stato da poco festeggiato il centenario) le osservazioni di Eddington furono di bassa qualità, prevalentemente per motivi meteorologici, mentre da Sobral il gruppo di Crommelin osservò l'eclisse in condizioni ottimali. Alla fine, analizzati i dati, Eddington e i suoi collaboratori costatarono che la luce delle stelle veniva effettivamente deflessa presso il bordo del disco solare, di un angolo stimato in 1",76. Questa fu la prima grande conferma della teoria einsteniana della Relatività Generale. L'annuncio che la teoria di Einstein aveva ricevuto la prima conferma sperimentale, dato il 6 novembre 1919 nel corso di una riunione congiunta dei due enti finanziatori, Royal Society e Royal Astronomical Society, ebbe immediata e ampia eco non solo nella comunità scientifica, ma anche su quotidiani e riviste sia britanniche sia statunitensi, consegnando definitivamente l'ex oscuro impiegato dell'Ufficio brevetti di Berna alla fama mondiale.

| Negativo originale della foto dell'eclisse del 29 maggio 1919 con evidenziate le posizioni delle stelle spostate rispetto al disco solare |
.
6.5 Gli orologi nel campo gravitazionale
Vogliamo ora determinare quali conseguenze avrà il moto di un'onda elettromagnetica in un campo gravitazionale. Sia f é la frequenza dell'onda ed h la costante di Planck (6,626 x 10–34 J s), l'energia trasportata da quest'onda é allora:
E = h f (6.1)
Noi sappiamo che il fotone, il quanto di luce introdotto da Einstein nel 1905, è privo di massa inerziale, ma ad esso si può perciò associare una massa dinamica mD, per via della celeberrima equazione di Einstein:
E = m c2
Tale equazione è stata dettagliatamente ricavata nel mio ipertesto dedicato alla Relatività Ristretta, cui rimando, e in particolare in questa pagina. Se dunque E è quella fornita dalla (6.1), avremo:
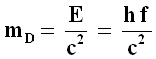

Salendo nel campo gravitazionale in piccolo, per quanto detto nel § 4.1 tale massa deve compiere un lavoro:

dove s é il dislivello colmato (abbiamo usato questa lettera per non confonderla con la costante h di Planck). Quindi la sua energia totale E diminuisce:
La formula é dimensionalmente giusta, perchè g s / c2 è privo di dimensioni. Ora, siccome E ' = h f ', dove f ' é la frequenza del quanto dopo aver colmato il dislivello s, avremo:
Se s é molto piccolo, anche (g s) é insignificante rispetto a c2, e la formula si riduce banalmente a f ' = f. Se però il campo gravitazionale é assai intenso ed il dislivello colmato é notevole, si hanno variazioni non trascurabili.
Poiché la disuguaglianza (g s) < c2 vale sempre, f ' é sempre minore di f. Perciò ne consegue che, salendo in un campo gravitazionale, la frequenza delle onde elettromagnetiche si sposta verso il rosso. Infatti, maggiore é la frequenza, più lontani si é dal rosso nello spettro. Si parla in tal caso di redshift gravitazionale.
La verifica sperimentale di questo importante fenomeno fu eseguita nel 1959 da Robert Pound (1919-2010) e Glen Anderson Rebka (1931-2015), che lavorarono in una torre alta 20 metri nel Jefferson laboratory dell'Università di Harvard (Massachusetts). La variazione risulta allora pari a:
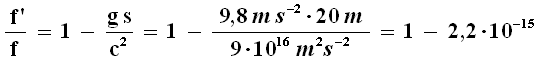
Variazione infinitesima, questa, che poté essere rilevata con un esperimento delicatissimo, grazie ad un provvidenziale fenomeno di restringimento delle linee spettrali noto come effetto Mossbauer. La variazione di frequenza é di circa 1 Hz.
Nel luglio 2019 poi Tuan Do, dell'Università della California a Los Angels e colleghi hanno pubblicato i risultati dell'osservazione della stella S0-2 che orbita intorno al buco nero supermassiccio che si trova al centro della Via Lattea, compiuta usando agli strumenti dell'Osservatorio Keck, nelle isole Hawaii. Do e colleghi hanno raccolto lo spettro della radiazione emessa da S0-2, mappando il suo moto orbitale in tre dimensioni e con una precisione senza precedenti e combinando i dati ottenuti con quelli raccolti negli ultimi 24 anni di osservazioni. Conclusione: il redshift gravitazionale rilevato dai dati spettrografici è perfettamente compatibile con le previsioni della relatività generale.

Salvador Dalì, "Les montres molles" (1931)
Estendendo i risultati ad una qualsiasi distanza R dalla massa M che genera il campo gravitazionale, per la (2.7) si ha:
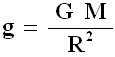
Se assumo s = R, cioè che l'onda elettromagnetica "cada" fino al centro della Terra, dalla (6.3) ricavo:
Ora, un elettrone che ruota intorno ad un nucleo può essere sfruttato per il funzionamento di un orologio atomico: la frequenza del moto elettronico é utilizzata per far spostare la lancetta (cioè per azionare il segnatempo). Ma se ci spostiamo verso l'alto in un campo gravitazionale, la frequenza, come si é visto, diminuisce. La frequenza é l'inverso del periodo: a quota maggiore gli orologi vanno quindi più rapidamente. Sulla base di quanto detto in precedenza, vale la relazione:
Questo ci aiuta a spiegare l'apparentemente assurdo spostamento verso il rosso della luce in un campo gravitazionale: il periodo dell'onda, a quote più alte, risulta leggermente maggiore di quello a quote più basse, quindi la frequenza apparentemente sembra diminuire; in realtà é sempre la stessa, é il tempo relativo che é diverso! Una notevole applicazione di questo fenomeno ad una serie di fantascienza (per la precisione "Stargate SG-1") verrà approfondita nella soluzione dell'esercizio 4, al termine di questo ipertesto. Così scrive in proposito Kip Thorne (1940-) nel suo saggio "La scienza di Interstellar - Viaggiare nello spazio-tempo":
« Nel 1912 Einstein ebbe una brillante ispirazione: comprese che il tempo viene incurvato dalle masse dei corpi pesanti, come la Terra o un buco nero, e che tale curvatura è responsabile della gravità. Espresse questa intuizione in quella che io chiamo la "legge della curvatura del tempo di Einstein", una formula matematica precisa che possiamo descrivere in termini qualitativi nel seguente modo: ogni cosa ama vivere dove invecchierà più lentamente, ed è lì che la gravità la attira. Quanto più è marcato il rallentamento del tempo, tanto più è forte l'attrazione gravitazionale. Sulla Terra, dove il tempo rallenta solo di qualche microsecondo al giorno, l'attrazione gravitazionale è modesta. Sulla superficie di una stella di neutroni, dove il tempo rallenta di qualche ora al giorno, l'attrazione gravitazionale è enorme. E sula superfcie di un buco nero, dove il tempo rallenta fino a fermarsi, la gravità è talmente gigantesca che nulla può sfuggirle, neppure la luce. »
A partire dal 1907, Einstein si mise a lavorare, seppur in modo discontinuo, sulla comprensione del fenomeno della gravità. Alla fine, nel 1912, ebbe una brillante ispirazione: comprese che il tempo viene incurvato dalle masse dei corpi pesanti, come la Terra o un buco nero, e che tale curvatura è responsabile della gravità. Espresse questa intuizione in quella che io chiamo la "legge della curvatura del tempo di Einstein"", una formula matematica precisa' che possiamodescrivere in termini qualitativi nel seguente modo: Ogni cosa ama vivere dove invecchierà più lentamente, ed è lì che la gravità la attira.Quanto più è marcato il rallentamento del tempo, tanto più è forte l'attrazione gravitazionale. Sulla Terra, dove il tempo rallenta solo di qualche microsecondo (milionesimo di se-condo) al giorno, l'attrazione gravitazionale è modesta. Sulla superficie di una stella di neutroni, dove il tempo rallenta di qualche ora al giorno, l'attrazione gravitazionale è enorme. E sula superfcie di un buco nero, dove il tempo rallenta fino a fermarsi, la gravità è talmente gigantesca che nulla può sfue-girle, neppure la luce.
Anche la variazione del tempo é stata verificata sperimentalmente: un aereo con a bordo un orologio atomico B, sincronizzato con uno a terra A, é stato portato ad alta quota e si é rilevata la differenza nei tempi da essi segnati, che riporto in questo diagramma disegnato da Enrica Soldavini:
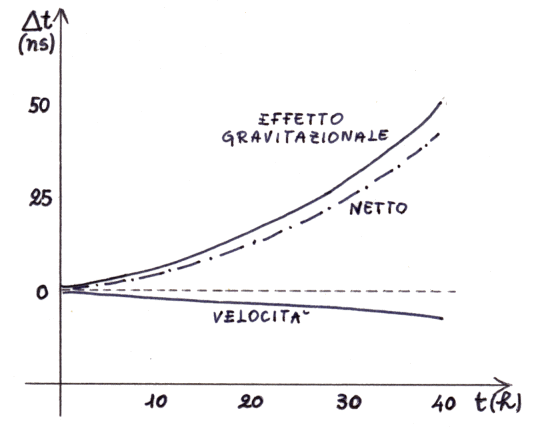
Considerando che dei 52,8 nanosecondi di variazione complessiva, circa 5,7 nanosecondi sono da attribuire all'effetto relativistico della dilatazione dei tempi, descritta in questa pagina di un altro mio ipertesto, si ottiene una differenza netta di + 47,1 nanosecondi in circa 40 ore. Confrontando A e B dopo che l'aereo é atterrato, si riscontra proprio una variazione lievissima di circa 48 nanosecondi. La precisione é di circa l'1 %! L'accuratezza migliorò ulteriormente nel 1976, quando Robert Vessot (1930-2018), dell'Università di Harvard, posizionò un orologio atomico su un razzo della NASA che sali a 10.000 chilometri di altitudine, e usò i segnali radio per confrontare la velocita del suo dicchettio con quella degi orologi a terra. Versot osservò così che il tempo a terra scorre più lentamente di circa 30 microsecondi che a 10.000 chilometri di altitudine, in perfetto accordo con la teoria di Einstein: il margine di incertezza era appena dello 0,007 %!
Ecco un'altra delle stupefacenti conseguenze della Relatività Generale. I nostri pronipoti, che un giorno si trasferissero a vivere in orbita terrestre, a gravità zero, o sulla Luna, dove la gravità é un sesto della nostra, invecchierebbero più velocemente di noi (che questo risulti un freno per la colonizzazione dello spazio?) Anzi, di più: chi abita ai piani più alti delle case, invecchia prima, sia pure di pochi microsecondi!
.
6.6 Le aste si accorciano!
Consideriamo ora due aste uguali, o almeno di uguale misura in uno stesso sistema di riferimento (nel vuoto cosmico, lontano da grandi masse), e portiamone una in prossimità di una massa M, alla distanza R dal suo baricentro. Se facciamo partire un raggio di luce da una estremità all'altra delle due aste, finché siamo nello stesso sistema, i tempi rilevati sono uguali: é l'unico mezzo che possediamo per poter stabilire l'uguaglianza delle due aste! Ma se un'asta é in un sistema gravitazionale, i tempi variano:
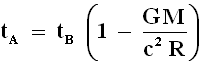
Ora moltiplico entrambi i membri per la velocità della luce c:
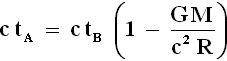
ma c tA = lA e c tB = lB. Ne consegue allora l'importantissima relazione:
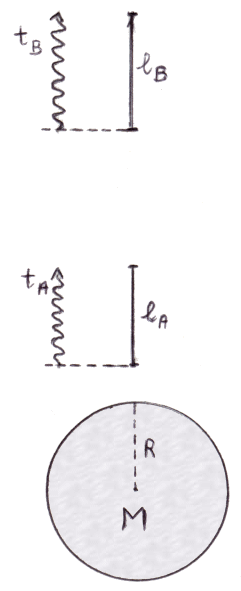
Essa ci dice che in un campo gravitazionale le aste si accorciano. Pare incredibile, eppure, quando passiamo da gravità zero ad un campo gravitazionale non trascurabile, si verificano gli stessi stranissimi fenomeni che è possibile rilevare quando si passa da un riferimento in quiete, o a bassa velocità, ad uno in moto con velocità paragonabile a quella della luce: le lunghezze e i tempi misurati in prossimità di masse risultano più corti, come spiegato in quest'altro ipertesto didattico. E questa risulta la più incredibile conseguenza del Principio di Equivalenza einsteniano.
Chi ha già consultato il mio ipertesto dedicato alla Relatività Ristretta conosce il paradosso dei due gemelli, uno dei quali resta sulla Terra mentre l'altro parte verso una stella lontana; al ritorno, quest'ultimo è assai più giovane del suo gemello. In pratica, i due gemelli vivono in due tempi diversi; ebbene, coloro che stanno sulla Terra e quelli che vivono a gravità zero vivono la stessa scioccante esperienza, come ci ha insegnato la Relatività Generale. Il sogno di Newton di uno spazio e di un tempo assoluti crolla così definitivamente. Tuttavia, i più attenti di voi si saranno forse accorti di un problema insito nel suddetto paradosso, che servì ai detrattori di Einstein per cercare di mettere in crisi la neonata Relatività. Se uno dei due gemelli si muove rispetto a quello rimasto sulla Terra, rispetto al sistema di riferimento dell'astronave si potrebbe ritenere fermo quello partito per il viaggio interstellare, ed in moto quello rimasto sul pianeta natale. Ma allora, non dovrebbe essere questo più giovane dell'altro? Sembra un paradosso insolubile, ed invece confutarlo é uno scherzo, proprio alla luce della Relatività Generale. I principi basilari della Relatività Ristretta valgono infatti solo in sistemi inerziali. Mentre però il gemello restato sulla Terra é sempre rimasto in un sistema inerziale, l'altro non lo ha fatto, perché in partenza dalla Terra, in fase di atterraggio sul pianeta alieno, in fase di ripartenza ed in fase di arrivo sulla Terra l'astronave accelera o decelera. Non esiste, dunque, un sistema inerziale rispetto al quale il razzo si trovi in quiete per l'intera durata del viaggio, e perciò questo non potrà mai essere considerato fermo! E così la simmetria tra i due gemelli si è rotta, e i fondamenti della Relatività Ristretta sono salvi.
Aggiungiamo che la dilatazione dei tempi nel campo gravitazionale è stata confermata con una precisione senza precedenti dai ricercatori del Joint Institute for Laboratory Astrophysics (JILA), frutto della collaborazione del National Institute of Standards and Technology (NIST) e dell'Università del Colorado a Boulder. Il livello di accuratezza di questo tipo di misurazioni è così elevato, secondo i ricercatori, che presto potrebbero aprirsi nuove opportunità per gettare un ponte tra fisica relativistica e fisica quantistica. L'idea di base è che le frequenze delle radiazioni emesse o assorbite dagli atomi su cui si basano gli orologi atomici seguano questa legge fisica, e che la loro estrema precisione consenta di rilevare gli effetti relativistici anche con differenze di quota molto limitate e in campi gravitazionali poco intensi. Ai ricercatori del JILA è bastata la separazione di un millimetro tra due atomi per testare la relatività generale (nel 2010 si era arrivati a una distanza di 33 centimetri). Ci sono riusciti tramite un apparato sperimentale inedito, costituito da un campione di 100.000 atomi di stronzio mantenuti a una temperatura di pochi Kelvin sopra lo zero assoluto e confinati in un reticolo ottico, cioè in una schiera di raggi laser incrociati. La configurazione dei laser era tale da consentire di controllare con estrema precisione gli stati energetici degli atomi del campione, e quindi le frequenze delle radiazioni emesse o assorbite. Dalle misurazioni è emersa una differenza nel "ticchettio" degli orologi a diverse quote di una parte per miliardo di miliardo, in linea con le previsioni della teoria della relatività generale. Tale differenza è emersa già dopo 30 minuti di raccolta dati, ma la significatività statistica ottimale è stata raggiunta dopo circa 90 ore: la misura è risultata 50 volte più precisa rispetto ai precedenti confronti tra orologi. Per le sue caratteristiche innovative, naturalmente, l'apparato sperimentale utilizzato offre un'occasione preziosa per collegare la fisica relativistica con la fisica quantistica, esplorando quest'ultima nello spazio-tempo curvo. Jun Ye, uno degli autori dello studio, ha affermato: « Se potessimo misurare la dilatazione dei tempi dieci volte meglio di così, saremmo in grado di vedere per intero le onde associate agli atomi attraverso la curvatura dello spazio-tempo. Essere in grado di misurare la differenza di tempo su una scala così piccola potrebbe permetterci di scoprire, per esempio, che la gravità interrompe la coerenza quantistica, il che potrebbe essere alla base del perché il nostro mondo su macroscala è classico ». Complimenti agli autori.
.
6.7 Euclide ha fallito
Man mano che ci addentriamo nella fisica della Relatività Generale, le nostre affermazioni si fanno sempre più sconcertanti. Siamo sicuri di camminare ancora coi piedi per terra, o stiamo volando tra le nubi aristofanee della matematica? Come si può fare per verificare sperimentalmente un'affermazione come quella precedente?
La difficoltà é evidente. Nel caso dei tempi, abbiamo utilizzato due orologi che, in diversi sistemi gravitazionali, sfasavano per poi mantenere la sfasatura dopo l'atterraggio dell'aereo. Ma nel caso delle lunghezze é diverso. Se sull'Everest un'asta é più lunga che nella fossa delle Marianne (la variazione é naturalmente piccolissima), portando lassù e laggiù un metro, esso parimenti s'allunga e s'accorcia. Riportando un'asta vicino all'altra, cambia il sistema ed esse riassumono la stessa lunghezza. Come si può verificare allora il nostro asserto?

Ricorriamo per questo ad un gedankenexperiment (in tedesco "esperimento concettuale"). Supponiamo che un geometra dotato di proprietà sovrumane misuri, con regoli di ugual lunghezza (o con lo stesso regolo, spostandolo continuamente), il diametro dell'orbita terrestre e poi, con gli stessi regoli, la sua circonferenza. Il geometra soprannaturale troverà, dividendo la misura C della circonferenza per quella D del diametro, il rapporto:
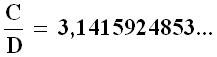
Questo rapporto, secondo le previsioni della geometria euclidea, dovrebbe invece essere:
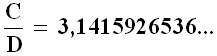
Per la prima volta, dunque, Euclide ha fallito: egli aveva previsto che il rapporto tra circonferenza e diametro di un cerchio fosse uguale a pi greco (π), ed invece si è registrato un errore di circa 60 parti per miliardo! Come si spiega la discrepanza? Perché la geometria euclidea non vale più? Alla luce di quanto si é detto prima, le aste che vengono allineate per misurare il diametro, essendo dirette secondo le linee di forza del campo gravitazionale in grande del Sole, subiscono la massima contrazione gravitazionale, e quindi occorreranno più regoli per misurare la stessa lunghezza nel caso in cui la massa solare non esistesse. Invece, i regoli della circonferenza sono perpendicolari alle linee di forza, e quindi la loro contrazione é nulla: perciò il numero di regoli é sempre lo stesso, anche supponendo di far sparire il Sole. Per questo, nel rapporto C / D, il diametro é maggiore di quanto non sarebbe nel caso in cui la massa non esistesse, e il rapporto é minore di quello determinato a priori, cioè del famoso pi greco. Ecco perché, nello spazio, la geometria euclidea non vale più. La Relatività Generale ha fatto cadere un'altra testa illustre!

Dante Alighieri sembra aver anticipato ancora una volta gli sviluppi della Fisica moderna quando, ormai giunto alla fine del suo viaggio ultraterreno, ci dice:
« Qual è il geometra che tutto s'affige
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige,
tal era io a quella vista nova... » (Par. XXXIII, 133-136)
È evidente che il "principio" di cui il geometra "indige", cioè "manca", per riuscire a misurare il cerchio, è proprio il pi greco, impossibile da determinare nella sua interezza perchè, essendo un numero irrazionale trascendente, ha infinite cifre decimali non periodiche, ma anche difficilissimo da misurare nell'universo che ci circonda, essendo il suo valore dipendente dalle masse che ci circondano!
Il risultato ottenuto si può spiegare anche così. Supponiamo di scavare una buchetta per terra e di porre su di essa un bastoncino. Due legioni di formiche attraversano la piccola buca, una sul bastoncino teso fra due estremi opposti e l'altra sul fondo. Se partono insieme, la prima schiera precederà la seconda, perché il tragitto più breve tra due punti é quello rettilineo. Se però la buca é ampia e poco profonda, anche la seconda schiera delle nostre formiche crederà di aver percorso il diametro della buca. In effetti lo ha fatto, ma... in un diverso sistema di riferimento!
Quindi, il risultato della diminuzione del valore di pi greco rispetto alle misurazioni teoriche può anche essere espresso dicendo che lo spazio si é curvato.
Dobbiamo cercare di capire bene la portata rivoluzionaria di questo nuovo modo di interpretare il campo gravitazionale di una massa. Se una formica geometra misurasse con opportuni regoli la circonferenza della buca ed il suo diametro sul bastoncino, troverebbe esattamente il rapporto pi greco. Se invece misurasse il rapporto C / D sul fondo della buca, constaterebbe con stupore che C / D < π, esattamente come abbiamo fatto noi. Ciò può essere descritto in un altro modo: la massa "deforma" lo spazio circostante, e ci costringe a cambiare la geometria necessaria a descriverlo.
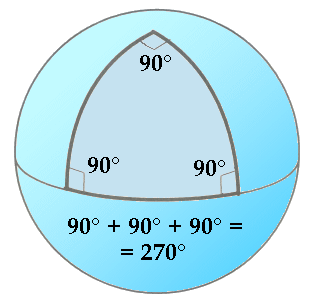
Tale affermazione può essere giustificata con alcune semplici osservazioni. Per un notissimo teorema della geometria euclidea, se misuriamo gli angoli di un triangolo disegnato su un piano, troviamo che la loro somma é esattamente π radianti, cioè 180°. Invece se il triangolo é disegnato su una sfera, si riscontra che tale somma é maggiore di π radianti! Per esempio, il triangolo formato da due meridiani perpendicolari e dall'equatore ha tre angoli retti, e la somma dei suoi angoli interni è di 270°, come si vede qui sotto a sinistra! Se invece misuriamo tale somma in un triangolo disegnato su una superficie a sella, come quella qui sotto a destra, si trova che anche essa risulta minore di π radianti. Per esempio, su tale superficie può essere disegnato un triangolo con tre angoli di 45°, la cui somma degli angoli interni vale perciò 135°!

Ricordiamo che tutta la geometria euclidea ruota intorno a cinque postulati fondamentali. Mentre però i primi quattro sono intuitivi:
I
) per due punti qualsiasi passa una retta e una sola;
II) la linea retta può essere prolungata indefinitamente;
III) dato un punto e una lunghezza, è possibile descrivere un cerchio che ha
come centro il primo e come raggio il secondo;
IV) tutti gli angoli retti sono uguali tra loro;
il quinto decisamente non lo è:
V) per un punto fuori di una retta passa una ed una sola parallela alla retta data.
Questo fatto diede adito, nei secoli, ad innumerevoli tentativi di dimostrare questo postulato. Alcuni tentarono di riformularlo in altro modo per poterlo dedurre dai primi quattro, ma fu tutto inutile. Chi pensò di aver risolto il problema fu l'italiano Girolamo Saccheri (1667-1733), che nel suo libro "Euclides ab omni naevo vindicatus" ("Euclide emendato da ogni neo") sostenne di averlo dimostrato per assurdo, negandolo ed essendo convinto di essere giunto a conclusioni incompatibili con i primi quattro postulati. In realtà, egli non aveva dimostrato nulla; semplicemente, aveva creato delle geometrie non euclidee., che seguono postulati diversi da quello testé enunciato. Il primo ad accorgersi che Saccheri aveva sconfinato senza volerlo al di fuori della geometria di Euclide fu il tedesco Carl Friedrich Gauss (1777-1855), uno dei più grandi matematici di ogni tempo, ma i primi a costruire una vera e propria geometria non euclidea, indipendentemente l'uno dall'altro, furono il russo Nikolaj Lobacevskij (1793-1856) nel 1829 e l'ungherese Janos Bolyai (1802-1860) nel 1832. Essi fondarono il lavoro su un postulato completamente diverso dal Quinto di Euclide:
Va) per un punto fuori di una retta passano infinite rette parallele ad una retta data.
Come realizzare in pratica questa strampalata geometria? In realtà è meno difficile di quanto sembri: basta chiamare "piano" quello che per Euclide è un cerchio, e "retta" ogni corda dello stesso cerchio (estremi esclusi). È facile verificare che i primi quattro postulati di Euclide valgono anche in questa geometria. Tuttavia, non vale più il famoso Quinto Postulato se definisco "rette parallele" due corde del cerchio che non si intersecano mai. Si consideri infatti la seguente figura:
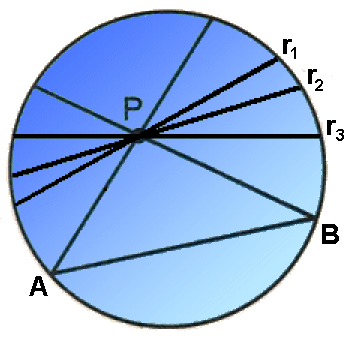
Il punto P non appartiene alla "retta" AB, ma come si vede ci sono infinite "rette" passanti per P (ad esempio r1, r2, r3) che non intersecano AB, e quindi ad esse "parallele"! Questa nuova geometria viene chiamata iperbolica. Si può dimostrare che in essa valgono ancora molti teoremi della geometria euclidea: ad esempio gli angoli opposti al vertice sono congruenti, ma non è più vero che la somma degli angoli interni di un triangolo è pari a 180°: è invece sempre minore di 180°.
Successivamente, sempre negando il Quinto Postulato, Bernhard Riemann (1826-1866) nel 1854 costruì un'altra geometria non euclidea, stavolta detta ellittica, in cui vale il seguente postulato alternativo:
Vb) per un punto fuori di una retta non si può condurre alcuna retta ad essa parallela.
Come riuscire in questa impresa? Basta chiamare "piano" quella che per Euclide è la superficie di una sfera S, e "rette" i suoi cerchi massimi, ad esempio T1 e T2, mentre "punti" sono le coppie di punti euclidei antipodi sulla sfera, come ad esempio E ed F nella figura seguente:
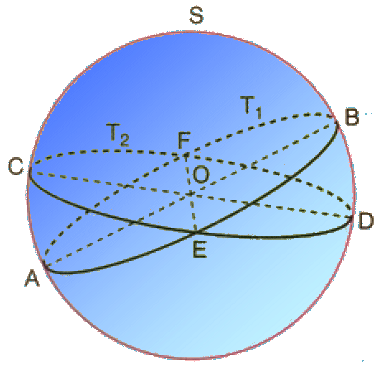
Come si vede, nessun cerchio massimo può evitare di intersecarne un altro, e dunque le rette parallele non esistono più, in accordo con il "nuovo" postulato di Riemann! Non è difficile dimostrare che in questa geometria non esistono triangoli simili, salvo quando sono anche congruenti; che da un punto ad una "retta" si possono condurre infinite perpendicolari; che due "rette" perpendicolari ad una stessa "retta" non sono parallele tra loro; e soprattutto che la somma degli angoli interni di un triangolo è sempre maggiore di 180°.
Come si vede, la geometria iperbolica di Lobacevskij e Bolyai sfrutta pur sempre figure piane come il cerchio che si sostituiscono al piano, mentre la geometria ellittica di Riemann abbandona il piano, costruendo la sua geometria su di una superficie curva. In questo caso si tratta in effetti della superficie tridimensionale di una sfera, ma il tutto può essere generalizzato ad una "superficie ad n dimensioni", che prende il nome di varietà di Riemann n-dimensionale. Viene introdotto in tale modo il concetto di curvatura dello spazio, giacché la varietà di Riemann è manifestamente una superficie curva. In particolare, la sfera viene chiamata una "varietà di Riemann a curvatura positiva", in quanto la somma degli angoli interni di un triangolo risulta maggiore di un angolo piatto. Allora la geometria euclidea, che è costruita dentro un piano, è una geometria a curvatura nulla, mentre la geometria iperbolica sopra descritta è una "varietà di Riemann a curvatura negativa", in quanto la somma degli angoli interni di un triangolo risulta minore di un angolo piatto. In pratica, la geometria costruita su una superficie sferica è sicuramente ellittica, mentre quella costruita su di un piano è inevitabilmente euclidea, e quella realizzata su di una superficie "a sella" è certamente iperbolica, come mostra lo schema seguente, opera di Enrica Soldavini:

In sintesi, si può affermare che la somma degli angoli interni di un triangolo é maggiore, uguale o minore di π radianti, a seconda che sia disegnata su di una superficie a curvatura positiva, nulla o negativa!
.
6.8 Un nuovo modo di concepire la gravità
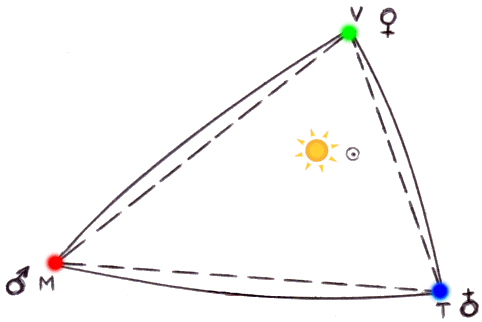
Ora, se congiungono la Terra, Venere e Marte con tre segmenti e si misurano gli angoli del triangolo che ha per vertici questi tre pianeti, si giunge ad una scoperta sconvolgente: la loro somma risulta maggiore di π radianti! Questo significa che il Sole attribuisce allo spazio circostante una curvatura positiva. Una verifica sperimentale rigorosa di questo fatto fu compiuta dall'astrofisico americano Irwin Shapiro (1929-) con il radiotelescopio di Haystack ( Westford, Massachusetts). Quest'ultimo infatti può venire usato per misurare le distanze planetarie, inviando ai pianeti un fascio di microonde per riceverle di ritorno dopo un certo tempo t. La distanza é data da ( c t / 2 ). Ora, Shapiro misurò la distanza di Venere e della Terra in opposizione (da parti opposte rispetto al Sole), quando il cammino delle onde RADAR é praticamente la somma del raggio dell'orbita terrestre e di quella venusiana, e trovò che il cammino effettivo é maggiore di quello previsto dalla geometria euclidea di circa 36 Km. Quale migliore conferma?
Tutti sanno che, in una superficie piana, e quindi in uno spazio euclideo, il cammino più breve tra due punti è un segmento di retta; tale cammino più breve di tutti gli altri prende il nome di geodetica. Ma, se le masse sono in grado di modificare in modo evidente la geometria del lo spazio circostante, questo varrà anche per le geodetiche, che muteranno in maniera sensibile! Un'efficace modellizzazione di questo fenomeno è la seguente. Se gioco a biglie sulla superficie piana del mio letto, una volta lanciate esse si muoveranno lungo traiettorie pressoché rettilinee, cioè lungo le geodetiche. Ma se sulla coperta pongo una pallina d'acciaio, con il suo peso essa deforma la superficie piana, incurvandola verso il basso. Se si lancia una biglia su questa coperta incurvata, la sua traiettoria non sarà più rettilinea ma curva, apparendo accelerata ed attratta dalla biglia centrale. In pratica i pianeti sono in moto intorno al sole perchè, nello spazio incurvato dalla fortissima gravità dell'astro, essi seguono le geodetiche della sua geometria non euclidea, che non sono linee rette, bensì proprio le coniche di cui abbiamo parlato nel § 4.3!

La curvatura dello spazio causata dalla gravità può spiegare benissimo anche la curvatura dei raggi di luce di cui si è discusso nel § 6.4: non sono essi che si incurvano, ma lo spazio in cui viaggiano. Normalmente essi procedono in linea retta, perchè nello spazio euclideo in cui noi ci troviamo a svolgere la nostra esistenza il cammino più breve tra due punti è costituito da una linea retta; nello spazio deformato dalla presenza di grandi masse, i raggi di luce continuano a seguire le geodetiche della geometria che lo descrive, ma esse non sono più rette, bensì curve assai più complesse, come mostrano i seguenti disegni di Enrica Soldavini:
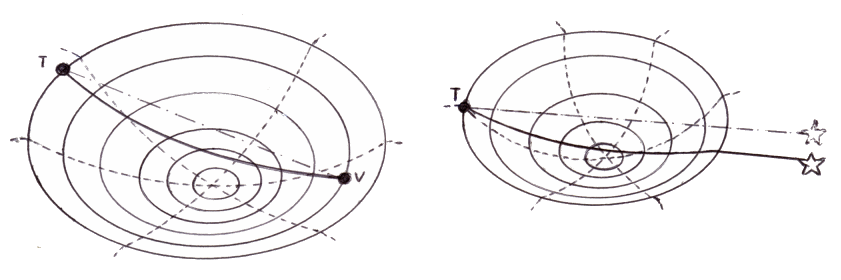
Come già successo trattando della Relatività Ristretta, Einstein cambia completamente la prospettiva dalla quale guardare l'universo. Isaac Newton infatti, come abbiamo detto nel § 2.2, descrisse i moti dei corpi nello spazio ipotizzando che tra due masse si eserciti una forza, chiamata forza di gravitazione universale; siccome essa dipende dall'inverso del quadrato della distanza fra le masse, i calcoli svolti nei § 4.2 e 4.3 ci hanno mostrato come tale descrizione ci porti a concludere che i pianeti orbitano intorno al Sole lungo orbite ellittiche. Invece Einstein giunge alla stessa conclusione togliendo di mezzo qualunque interazione reciproca: il pianeta non segue una traiettoria ellittica perchè è attratto dal Sole, ma perchè quest'ultimo con la sua massa deforma la geometria dello spazio-tempo, e nella nuova geometria la geodetica non è più una linea retta. In assenza di forze, secondo il Principio di Inerzia, il pianeta continua a seguire una geodetica dello spazio-tempo, ma essa ora è curvilinea e non più rettilinea! Tutto questo si può sintetizzare efficacemente affermando che Albert Einstein ha geometrizzato la gravitazione universale, trasformandola da una descrizione dinamica (cioè sotto forma di forza) ad una puramente geometrica. Questa rappresenta la maggiore fra tutte le intuizioni di Einstein, tanto che il fisico Richard P. Feynman ebbe a commentare: « Non riesco proprio a capire come abbia fatto a venirgli in mente! » Bisogna però tenere conto del fatto che il genio di Ulm non sarebbe mai arrivato ad una tale intuizione, senza l'aiuto di un matematico romagnolo, Gregorio Ricci Curbastro (1853–1925), fondatore del calcolo differenziale assoluto, una nuova branca della matematica con la quale Einstein fu in grado di descrivere la nuova struttura tensoriale dello spazio-tempo curvo. Le equazioni gravitazionali di Einstein, alla base della Relatività Generale, sono infatti delle equazioni tensoriali, come vedremo nel § 7.8.

Gregorio
Ricci Curbastro, l'italiano che anticipò
le intuizioni di Einstein (tratto da questo
sito)
Trafiletto del "Corriere
della Sera" del 28 ottobre 1921 che
annuncia l'incontro a Padova tra Einstein e Ricci Curbastro
La prova definitiva che le intuizioni di Einstein sulla curvatura dello spazio erano valide è venuta dal satellite NASA Gravity Probe B, lanciato il 20 aprile 2004, con lo scopo di misurare la curvatura dello spazio-tempo in prossimità della Terra. Allo scopo sono stati utilizzati quattro giroscopi puntati verso IM Pegasi, una stella binaria nella costellazione di Pegaso. Essi sono costituiti da sfere di quarzo rivestite con uno strato sottilissimo di niobio, del diametro di 3.8 centimetri ed immerse nell'elio fluido ad una temperatura inferiore ai 2 Kelvin, in modo da minimizzare l'interferenza molecolare. Questi giroscopi sono gli oggetti sferici più precisi mai realizzati, tanto da differire dalla sfera perfetta per meno di quaranta diametri atomici (meno di 10 nanometri): se il pianeta Terra fosse altrettanto sferico, le montagne più alte sarebbero alte solo 2,4 metri! Esse sono tenute sospese tramite campi elettrici, fatti ruotare usando un flusso di gas elio, ed i loro assi di rotazione sono rilevati monitorando il campo magnetico dello strato di niobio superconduttore. I giroscopi sono liberi da ogni perturbazione, in modo tale da fornire un sistema di riferimento spazio-temporale quasi perfetto.
L'esperimento ha verificato con estrema precisione i piccoli cambiamenti nella direzione di rotazione dei quattro giroscopi lungo l'orbita intorno alla Terra a 650 km di altitudine, attraversando direttamente sopra i poli. Ora, gli assi dei giroscopi dopo una rivoluzione completa non hanno più indicato la stessa esatta direzione di prima, segno inequivocabile del fatto che lo spazio-tempo circostante la Terra è stato deformato dalla massa di quest'ultima. La sensibilità dei giroscopi era dell'ordine del milliarcosecondo, il che corrisponde a misurare lo spessore di un foglio di carta osservato da una distanza di circa 160 chilometri. Nel maggio 2011 Francis Everitt, fisico dell'università di Stanford e a capo del progetto, ha pubblicato i risultati dell'esperimento, che confermavano in pieno le previsioni di Albert Einstein con una precisione di una parte su diecimila, la verifica più rigorosa mai fatta fino ad oggi sulle previsioni della Relatività Generale!
E non è tutto. Nel 2014 Guglielmo Tino e i suoi colleghi del Laboratorio Europeo di Spettroscopia non Lineare (LENS), dell'Università di Firenze e dell'Istituto Nazionale di Fisica Nucleare (INFN), hanno eseguito la prima misura diretta della curvatura del campo gravitazionale prodotta dalle masse! Per la precisione, Tino e compagni hanno misurato per la prima volta la derivata seconda, cioè la variazione del gradiente, del campo gravitazionale rispetto alla posizione, che corrisponde alla curvatura: questa quantità fisica è sensibile alla presenza di masse vicine. Avendo sviluppato nuovi sensori quantistici atomici, i ricercatori dell'INFN hanno misurato dapprima il valore della costante di gravitazione universale G con una precisione senza precedenti, poi verificato il principio di equivalenza, cioè l'uguaglianza tra la massa inerziale e la massa gravitazionale, e infine rivelato la curvatura del campo gravitazionale. In quest'ultimo esperimento, l'apparato sperimentale era sostanzialmente un'evoluzione dell'apparato sperimentale MAGIA, utilizzato nella misurazione di G. In esso, nuvole di atomi di rubidio raffreddati alla temperatura di pochi milionesimi di grado sopra lo zero assoluto utilizzando luce laser, vengono lanciate verso l'alto nel vuoto all'interno di una "fontana atomica". In cima a quest'ultima, è posta una massa di tungsteno di circa 500 chilogrammi, che ha la funzione di "massa sorgente", che produce la curvatura cercata. Grazie alla tecnica di interferometria atomica, in modo analogo a quanto si fa con le tecniche interferometriche ottiche, si può rilevare l'interferenza tra due onde di materia di un atomo, precedentemente separate tra loro da impulsi laser. La presenza del campo gravitazionale modifica il segnale di interferenza atomica. Però Guiglielmo Tino ha lanciato verso l'alto tre nuvole, invece di due, in modo da misurare simultaneamente l'accelerazione dei loro atomi: sottraendone a due a due i valori si elimina il contributo dell'accelerazione di gravità, che è uguale per tutti, trovando il contributo della sua derivata prima, cioè del gradiente, mentre sottraendo tra loro le tre differenze si elimina anche l'effetto del gradiente, evidenziando così il contributo della derivata seconda, cioè del gradiente del gradiente, legata alla curvatura. Il risultato ha dimostrato che questi nuovi sensori quantistici atomici consentano di misurare con estrema precisione i parametri fondamentali della Relatività Generale.
.
6.9 Caccia al pianeta introvabile
Una sola prova sperimentale della relatività generale era nota prima della sua formulazione da parte di Einstein: la precessione della linea degli apsidi di Mercurio. La linea degli apsidi, da noi già introdotta nel § 4.4, è quella che congiunge perielio ed afelio passando per il Sole; il fenomeno or ora citato consiste quindi nella lenta rotazione del perielio del primo pianeta attorno al Sole. Il moto orbitale di questo pianeta assomiglia insomma ad una stella di Natale, piuttosto che ad un'ellisse o ad un'altra conica come quelle da noi descritte nel § 4.3! Tale fenomeno, come oggi sappiamo, é proprio di tutti i pianeti, ma a quei tempi quello di Mercurio era l'unico noto, essendo esso stesso di lievissima entità: appena 43'' in un secolo.
Urbain Le Verrier, lo stesso astronomo che aveva previsto l'esistenza di Nettuno, come abbiamo spiegato nel § 2.7, tentò di ripetere lo stesso exploit per Mercurio, ipotizzando l'esistenza di un nuovo pianeta, Vulcano, più vicino al Sole di Mercurio e quindi invisibile, che ne perturberebbe l'orbita trascinandola. Il 26 marzo 1859 l'astronomo dilettante francese Edmond Modeste Lescarbault (1814-1894) annunciò di aver osservato il pianeta Vulcano sul bordo del disco solare. Sulla base delle indicazioni di Lescarbault, Le Verrier calcolò la posizione, l'orbita, le dimensioni e la distanza dal Sole di Vulcano: la distanza media dal Sole sarebbe stata di 21 milioni di chilometri (appena 0,14 unità astronomiche), il periodo di rivoluzione di soli 19 giorni e 17 ore, e l'inclinazione dell'orbita sul piano dell'eclittica risultava pari a 12° 10': l'elongazione dal Sole non sarebbe stata superiore agli 8 gradi. Purtroppo "Vulcano" risultò essere molto più piccolo di Mercurio, talmente piccolo da non poter giustificare le anomalie nell'orbita di quest'ultimo. Il mondo scientifico si divise così tra quanti sostenevano l'esistenza di Vulcano e gli scettici secondo cui l'astro osservato da Lescarbault era soltanto un asteroide di passaggio, o addirittura una macchia solare scambiata per un pianeta.
Durante l'eclisse solare totale del 29 luglio 1878, James Craig Watson (1838-1880), direttore dell'Osservatorio di Ann Arbor (Michigan), affermò di aver visto un pianeta intramercuriale molto vicino al punto in cui i calcoli di Le Verrier avevano previsto che avrebbe dovuto trovarsi Vulcano. Anche l'astronomo francese Aristide Coumbrary e l'astrofilo Lewis Swift di Rochester (New York) affermarono di aver individuato Vulcano. Successivamente si verificarono altre osservazioni del misterioso pianeta, ma alcune di esse non corrispondevano alle posizioni calcolate da Le Verrier, tanto che alcuni astronomi ipotizzarono l'esistenza di più di un corpo celeste o addirittura di una fascia di asteroidi intramercuriale. Purtroppo di Vulcano si impossessarono subito astrologi, maghi, esoterici, massoni e seguaci delle dottrine teosofiche che tanto andavano di modo a fine ottocento, screditando l'ipotesi Vulcano.
Arriviamo così al 1916 e alla formulazione delle equazioni gravitazionali di Einstein. Risolvendo le equazioni del moto ricavate da queste ultime, scopriamo che la traiettoria di una massa immersa nell'intensissimo campo gravitazionale solare, come é Mercurio, non è data dalla (4.10), da noi ricavata sulla base della legge di gravitazione universale di Newton, ma da un'equazione polare ben diversa:
dove r è il raggio vettore del pianeta, cioè la sua distanza dal Sole; θ è l'anomalia, cioè l'angolo spazzato dal raggio vettore rispetto ad una direzione prefissata come origine; ed ε è una costante molto piccola, data da:
dove a è il semiasse maggiore dell'orbita, c la velocità della luce, G la costante di gravitazione universale ed M la massa solare, da noi ricavata nel § 2.5. Osserviamo che il minimo di r, cioè il perielio del pianeta, si ha in corrispondenza dei massimi di cos (θ – ε θ), cioè quando:
cos (θ – ε θ) = 1
ciò avviene quando θ – ε θ = 2 π n ( n = 1, 2, 3... ) Allora due massimi successivi sono separati da un'anomalia pari a:
Questo ha un'importanza fondamentale, perchè ci dice che due perieli successivi non si presentano più dopo una rivoluzione di 2π radianti! Ora, essendo ε molto piccola, si ha:
![]()
e quindi:
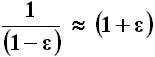
La (6.9) mi dice allora che:
![]()
Questo significa che il perielio dei pianeti si ripresenta leggermente spostato in avanti ad ogni giro; per la (6.8) ad ogni giro guadagna un angolo ε π, pari a:

Mercurio visto dalla sonda MESSENGER
Come si vede, il fenomeno è tanto più accentuato quanto più a è piccolo, cioè quanto più il pianeta è vicino al Sole; lì, infatti, lo spazio è maggiormente curvato, trovandoci più prossimi alla massa che "deforma" lo spazio. Mercurio dista in media 0,39 unità astronomiche dal Sole, cioè 58 milioni di Km. Sostituendo i valori numerici nella (6.10), si ha:
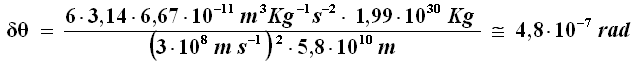
Si tratta di uno spostamento piccolissimo e non rilevabile. Ma se accumulo per un secolo? L'anno di Mercurio vale circa 88 giorni, per cui:
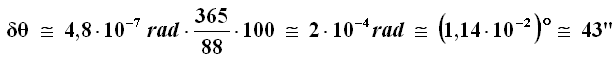
Ritroviamo così proprio la precessione secolare di Mercurio! Dunque essa non è dovuta all'esistenza di un pianeta fantasma, ma trova la sua naturale spiegazione nell'ambito della Relatività Generale. E questo mise la pietra tombale sulle ricerche del pianeta Vulcano. Per gli altri pianeti, i valori calcolati sono assai minori: 8",6 per Venere, 3",8 per la Terra, 1",3 per Marte.
A dir la verità, gli astronomi moderni non escludono del tutto la possibilità che possano essere presenti uno o più corpi celesti all'interno dell'orbita di Mercurio, battezzati asteroidi vulcanoidi, ma le molte osservazioni effettuate anche con mezzi sofisticati come foto da satellite, non hanno dato alcun esito; la sonda MESSENGER potrebbe forse osservarne qualcuno. Comunque, il mito di Vulcano continua a vivere tuttora: ancora nel 1965 alcuni fisici misero in dubbio la validità delle conclusioni ora tratte per Mercurio, poiché secondo loro il Sole non è una sfera perfetta, ma anzi fortemente schiacciata ai poli, e quindi la fascia equatoriale del Sole potrebbe comportarsi come il fantomatico Vulcano, e perturbare il moto di Mercurio. Inoltre lo scrittore di fantascienza Gene Roddenberry (1921-1991), creatore dell'universo di Star Trek, ha dato proprio il nome di Vulcano all'immaginario pianeta extrasolare patria del celeberrimo Mister Spock!

Ancora una parola sul moto funambolico del primo pianeta del Sistema Solare, In effetti, in base alla (6.7) la traiettoria di Mercurio e degli altri pianeti non é chiusa, in chiaro contrasto con quanto da noi visto nei § 4.3 e 4.4. Or, bisogna tenere conto del fatto che, come detto nell'ipertesto dedicato alla Relatività Ristretta, le teorie precedenti di Galileo e Newton non vengono superate, ma anzi completate da quelle nuove di Einstein, che le comprendono come casi particolari. La Relatività Ristretta deriva da quella Generale allorché si ponga l'accelerazione nulla, cioè nel caso di sistemi inerziali, mentre la teoria classica di Newton rientra in quella einsteniana allorché le velocità sono molto più piccole di quella della luce. Si può insomma dimostrare che le complesse equazioni tensoriali di Einstein si riducono a quella classica di Newton allorché si compie un'approssimazione numerica. Se però si tiene conto dei primi termini trascurati, la famosa legge di Newton data dalla (2,6):

andrebbe così corretta:

Come si vede, alla legge di Newton si ritorna togliendo di mezzo i decimali e prendendo solo r2. Ora però si può dimostrare che, per noti principi della meccanica, la traiettoria di un punto materiale soggetta ad un campo di forze può risultare chiusa se e soltanto se la forza é centrale, se cioè dipende dalla sola distanza da un punto fisso, e se é direttamente proporzionale alla distanza dal centro (il caso della forza di richiamo elastico) o all'inverso del quadrato della distanza dal centro ( la forza di gravitazione newtoniana e la forza elettrostatica coulombiana). Questo ci aiuta allora a capire perché il perielio di Mercurio precede attorno al Sole: dato che la forza non dipende più dall'esatto inverso del quadrato di r, la traiettoria non può più essere chiusa, come risultava dalla teoria classica, ed assume la forma asteroidale raffigurata qui sopra!

.
6.10 La croce nel cielo
Un altro fenomeno previsto dalla Relatività Generale è la cosiddetta lente gravitazionale. Quello che vedete raffigurato qui sopra è il quasar G2237 +0305, un oggetto del profondo cielo (il quasar più vicino dista da noi un miliardo di anni luce!) che emette tanta luce quanta una galassia, per ragioni ancora ignote: secondo alcuni nasconde al suo interno un immenso buco nero. Come si vede, questo quasar ha un'incredibile forma a croce: com'è possibile? In realtà si tratta di un'illusione ottica. Una galassia a noi molto più vicina del quasar, in questo caso la galassia ZW 2237 +030, scoperta dall'americano John Peter Huchra (1948–2010), è interposta fra noi e l'oggetto più lontano. La sua grande massa curva la luce del quasar, in modo da provocare un'amplificazione del segnale luminoso simile a quella causata da una lente di vetro con la luce visibile, nonché una moltiplicazione dell'immagine, come si vede nello schema sottostante. Einstein aveva previsto questo fenomeno fin dal 1937, ma esso fu osservato per la prima volta solo il 29 marzo 1980.
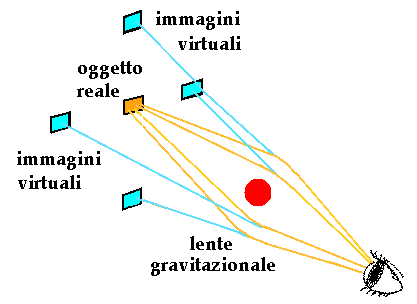
Se poi la sorgente luminosa ed il corpo celeste che funge da lente gravitazionale sono posti esattamente sulla stessa linea di vista rispetto all'osservatore, in conseguenza della simmetria circolare della configurazione ottica si osservano non delle immagini multiple della sorgente, disposte a formare una croce, ma addirittura un anello luminoso centrato sulla posizione in cielo della lente gravitazionale: è quello che si chiama un anello di Einstein! Esso è stato effettivamente osservato nell'ammasso di galassie Abell 1689, nella Costellazione della Vergine, perchè quest'ultimo con la sua grande massa riesce a trasformare in anelli la luce di remotissime galassie distanti da noi ben 11 miliardi di anni luce!

Anelli di Einstein visti dallo Hubble Space Telescope
Secondo molti, un buco nero (vedi § 5.7) potrebbe essere individuato grazie all'effetto di lente gravitazionale da esso provocato. Nella ricostruzione sottostante si vede il probabile aspetto della galassia Via Lattea vista dalla Terra, se davanti ad essa passasse un buco nero con una massa pari a dieci volte quella del Sole, posto a 600 km di distanza da noi. In questo caso però sarebbe necessaria un'accelerazione pari a 400 milioni di volte quella della gravità terrestre, per mantenere costante la nostra distanza da esso, senza venire risucchiati! Della relatività generale applicata ai buchi neri riparleremo nel § 7.8.

Vicino a un buco nero la gravità è talmente intensa e lo spazio-tempo è così incurvato, che i raggi di luce rimangono intrappolati in orbite esterne all'orizzonte degli eventi, compiendo numerose rivoluzioni attorno al buco nero prima di riuscire a sfuggire; le loro orbite sono instabili, perché alla fine i fotoni riescono sempre a fuggire via, a differenza dei fotoni catturati all'interno dell'orizzonte degli eventi, che non potranno mai uscirne. Per indicare questa luce temporaneamente intrappolata, alcuni astrofisici usano l'espressione "guscio di fuoco" che circonda un buco nero. Nel caso di un buco nero non rotante, il guscio di fuoco è una sfera con un raggio una volta e mezza maggiore di quella dell'orizzonte degli eventi. La luce intrappolata viaggia più e più volte attorno a questa stera muovendosi lungo dei cerchi massimi; nel famoso film "Interstellar" (2014), ciò che si vede attorno al buco nero Gargantua è proprio un'ottima simulazione computerizzata del guscio di fuoco intorno ad esso!
Un'ulteriore conferma delle previsioni della Relatività Generale è venuta nel 2008 dagli astronomi del Gruppo Pulsar dell'Osservatorio di Calgliari, facenti parte dell'Istituto Nazionale di Astrofisica. Essi hanno effettuato ben quattro anni di osservazioni con il radiotelescopio di Green Bank, in West Virginia (il secondo più grande del mondo dopo quello di Arecibo) di un sistema binario, J0737-3039, posto a 1800 anni luce dalla Terra e formato da due pulsar in rapidissima rotazione l'una intorno all'altra. Analizzando la scomparsa dell'impulso della prima pulsar, periodicamente eclissata dalla magnetosfera della compagna, gli astrofisici hanno potuto misurare il moto della seconda pulsar, scoprendo che durante la rotazione essa subisce un leggero e ciclico mutamento di inclinazione, con un periodo di circa settant'anni. L'osservazione si è rivelata in perfetto accordo con le previsioni della teoria di Einstein, in barba a quanti ancor oggi mettono in dubbio la validità delle sue ricerche.
Ma non è tutto. Il telescopio spaziale Hubble della NASA e il Very Large Telescope dell'European Southern Observatory, in Cile, hanno realizzato nel 2018 la più accurata verifica sperimentale della teoria generale della relatività di Albert Einstein mai ottenuta finora al di fuori del sistema solare. Il merito va a Thomas Collett dell'Institute of Cosmology and Gravitation dell'Università di Portsmouth e colleghi di una collaborazione internazionale. « Se conosciamo la massa della galassia in primo piano, la separazione tra le diverse immagini dell'oggetto distante dovute all'effetto di lente gravitazionale ci dice se la relatività generale è la teoria gravitazionale corretta su scale galattiche », ha spiegato proprio Thomas Collett, primo autore dello studio. Attualmente sono note centinaia di lenti gravitazionali, ma la maggior parte di esse è troppo distante per misurare in modo preciso la loro massa, e così non possono essere usate per una verifica accurata della relatività generale. Fa eccezione la galassia ESO 325-G004, a 500 milioni di anni luce di distanza dalla Terra. « Abbiamo usato i dati del Very Large Telescope per misurare la velocità di movimento delle stelle di ESO 325-G004, un parametro che ha permesso di stimare la massa di questa galassia », ha aggiunto Collett. « Poi abbiamo confrontato questa massa con le separazioni delle immagini di lente gravitazionale forte osservate con Hubble; il risultato coincide con la previsione della relatività generale entro un errore del nove per cento. Si tratta della più precisa misurazione extrasolare della relatività generale ottenuta finora ».
Come se non bastasse, nel 2021 i ricercatori dell'università di Stanford hanno osservato per la prima volta i « brillamenti di raggi X » dietro ad un buco nero supermassicci al centro di una galassia distante 800 milioni di anni luce. Il materiale che cade in un buco nero supermassiccio alimenta una fonte di raggi X continua, e dà così origine ad una corona intorno al buco nero. Ora, secondo Albert Einstein l'attrazione gravitazionale dei buchi neri piega i raggi di luce intorno ad essi, e per la prima volta gli astronomi hanno potuto osservare cosa si trova dietro a questi misteriosi corpi celesti. Cinquant'anni fa, quando gli astrofisici hanno iniziato a speculare su come il campo magnetico potrebbe comportarsi vicino a un buco nero, non avevano idea che un giorno avremmo avuto le tecniche per osservarlo direttamente. Se siamo in grado di vedere ciò che c'è dietro ad un buco nero, è perchè esso sta deformando lo spazio, piegando la luce e torcendo i campi magnetici intorno a sé. Einstein ha visto giusto ancora una volta.
.
6.11 Il motore che curva lo spazio
Chiudiamo con un divertissement, che forse però è meno fatuo di quanto si possa credere di primo acchito. Nel § 5.6 si è parlato del progetto Dedalus, che potrebbe spingere un'astronave fino a un decimo della velocità della luce. Alla luce di quanto detto in questo capitolo, tuttavia, vi potrebbe essere un'altra strada per raggiungere le stelle. Anziché accelerare per coprire grandi distanze, si potrebbero accorciare le distanze medesime. Questo risultato potrebbe essere ottenuto generando una distorsione spaziotemporale in grado di contrarre lo spazio davanti all'astronave e dilatarlo dietro di essa. Il classico paragone è quello con una formica che cammina sopra un elastico fissato tra due chiodi; normalmente la formica, per andare da chiodo a chiodo, dovrebbe camminare per un tragitto equivalente alla lunghezza dell'elastico. Ma, se l'elastico viene accorciato davanti alla formica e allungato dietro di essa, seguendola nel suo spostamento, l'insetto sarà andato da chiodo a chiodo camminando per un tragitto assai inferiore alla lunghezza complessiva dell'elastico, benché localmente esso non abbia potuto rilevare nessuna modifica dell'elastico.
Un motore in grado di ottenere questo risultato viene chiamato propulsore a curvatura (warp drive in lingua inglese), ed è stato reso celebre dalla saga di Star Trek, nella quale costituisce la "scappatoia" per superare le distanze interstellari (secondo il film "Star Trek: Primo Contatto", il primo volo a curvatura della storia sarebbe avvenuto il 5 aprile 2063 sopra il Montana). Può sembrare assolutamente incredibile, ma nel maggio 1994 il fisico messicano Miguel Alcubierre (1964-) in un celeberrimo articolo intitolato "Hyper-fast travel within general relativity" propose un modello teorico che permetterebbe di viaggiare più velocemente della luce senza violare il principio fisico che nulla possa viaggiare localmente più veloce della luce. Si tratta di una soluzione delle equazioni gravitazionali di Einstein chiamata "metrica di Alcubierre", secondo la quale sarebbe possibile trasportare un volume di spazio piatto all'interno di una "bolla" di spazio curvo. Questa bolla verrebbe spinta in avanti da una espansione locale dello spazio-tempo dietro di essa, e da una contrazione opposta di fronte ad essa, in modo che teoricamente una navicella spaziale sarebbe mossa dalle forze generate dalle modifiche da essa stessa apportate allo spazio-tempo. La soluzione di Alcubierre è corretta ed è in accordo con i principi della Relatività Generale, ma è inutile dire che il suo motore a curvatura, forse la prima applicazione ingegneristica della Relatività Generale, è oggi del tutto irrealizzabile, vista l'impossibilità pratica di creare una distorsione spaziotemporale controllata, sia per l'immensa energia necessaria allo scopo (nella saga di Star Trek si usano motori ad antimateria, assolutamente fuori della nostra portata), sia perchè non abbiamo idea di come evitare di venire stritolati dalle immense forze in gioco, paragonabili a quelle che si registrano nei pressi di un buco nero. Inoltre l'idea di Alcubierre richiede la generazione di un campo di densità di energia negativa, che equivale a richiedere una massa negativa, oggi del tutto fantascientifica. Inoltre un articolo del 2009 di Carlos Barceló, Stefano Finazzi e Stefano Liberati, sostiene che la propulsione di Alcubierre a velocità superiori a quella della luce è impossibile perché si genererebbero temperature estremamente elevate causate dalla radiazione di Hawking che distruggerebbero qualsiasi cosa all'interno della bolla, oltre che destabilizzarla. Inoltre un'astronave che sfrutta la propulsione di Alcubierre, una volta giunta a destinazione, dovrebbe decelerare dalla velocità superluminale a quella subluminale, e nel farlo rilascerebbe le particelle che la bolla aveva raccolto durante il viaggio sotto forma di getti di radiazioni altamente energetiche, tali da distruggere qualsiasi cosa si trovi direttamente di fronte all'astronave. Insomma, per parecchio tempo ancora dovremo accontentarci di vedere sfrecciare l'Enterprise sugli schermi televisivi, prima di poter effettivamente arrivare là dove nessuno è mai giunto prima...

L'Enterprise NX-01, prima delle navi con questo nome
.
Se non vi ho stancato con questa lunga cavalcata attraverso i fondamenti della Relatività Generale, vi consiglio di cliccare qui e di passare con me al prossimo capitolo, nel quale vedremo come questa ardita teoria preveda la distribuzione della materia e dell'energia dell'universo, e come possa prevedere il fatto che essa si trova in perenne espansione. Per tornare all'indice, invece, il link è questo.
![]()