![]()
|
"San Lorenzo, io lo so perché tanto G. Pascoli, "Myricae", 1903 |
.
4.1 In termini di energia
La (3.5) ci ha portato a concludere che il campo gravitazionale in grande è conservativo, dipendendo il lavoro solo da rA e da rB, non da tutti i punti intermedi. Ora vedremo quale importante conclusione si può trarre da questa formula. Ritorniamo per un attimo al campo gravitazionale in piccolo. Si è detto che, per superare un dislivello h, una massa deve compiere un lavoro L = m g h, essendo g l'accelerazione di gravità, che nel campo gravitazionale in piccolo è costante in ogni punto.
Ora, supponiamo che, rispetto ad una quota di riferimento, la sommità A del piano inclinato disegnato nel capitolo precedente si trovi a quota hA, e il punto di arrivo B si trovi a quota hB. Un esempio potrebbe essere rappresentato da un impianto idroelettrico: A è il punto in cui la condotta forzata parte dalla diga, B è quello dove si trova la turbina; se A si trova ad una quota di 1200 m sul livello del mare e la turbina a una quota di 400 m, è evidente che hA = 1200 m, hB = 400 m ed h = hA – hB = 800m. Nulla però mi proibirebbe di porre il livello zero dove vi è la turbina; allora avremmo hA = 400 m, hB = 0 m, ed h = hA – hB = 400 m. Un'alternativa sarebbe porre il livello zero in corrispondenza della diga; allora avremmo hA = 0 m, hB = – 400 m, e h = hA – hB = 0 – ( – 400) = 400 m.
Ne consegue che, ai fini del calcolo del lavoro, non ha alcuna importanza dove io pongo la quota pari a zero, poiché ciò che conta è solo e soltanto il dislivello:
L = m g (hA – hB)
Ora, però, quest'espressione può così essere riscritta:
L = m g hA – m g hB
L'espressione m g hA dipende solo dal punto A, l'espressione m g hB dipende solo dal punto B. La tentazione è perciò quella di introdurre una nuova grandezza, chiamata energia potenziale gravitazionale in piccolo, la cui espressione analitica è:
EPg = m g h
dove h è l'altezza rispetto a un certo livello di riferimento, scelto arbitrariamente. In tal modo il lavoro può così essere espresso:
L = EPgA – EPgB
In altre parole, nei campi conservativi è possibile introdurre una grandezza chiamata energia potenziale, il cui valore cambia da un punto all'altro del campo. Il lavoro per muovere una massa da A a B è pari all'energia potenziale nel punto iniziale meno quella nel punto finale. Siccome con ΔEP si indica in fisica la variazione di EP calcolata come il valore finale meno quello iniziale, avremo:
L = – ΔEPg
L'energia potenziale può essere introdotta solo se il campo è conservativo, poiché quest'espressione permette di ricavare il lavoro come differenza tra i valori di energia potenziale nei due estremi; se invece il campo non fosse conservativo, il lavoro dipenderebbe da tutti i punti intermedi, e il concetto di energia potenziale non avrebbe senso. È possibile far vedere inoltre che il campo conservativo è caratterizzato dalla conservazione dell'energia meccanica totale (somma di energia cinetica ed energia potenziale), da cui il nome di "campo conservativo".
Naturalmente è possibile introdurre un'energia potenziale anche nel campo gravitazionale in grande, essendo esso conservativo. Basta partire dalla (3.5) per definire in maniera naturale:
Il segno meno è necessario per poter scrivere L = – ΔEPg come nel campo gravitazionale in piccolo. L'andamento di questa espressione in funzione della distanza dal centro è tabulato qui sotto:
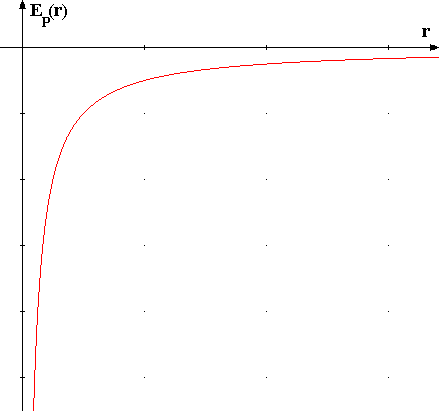
Per chi conosce i rudimenti dell'Analisi Matematica, un campo di forze è definito conservativo se si può esprimere come gradiente di un potenziale, cioè se esiste una funzione energia potenziale tale che, nel nostro caso:
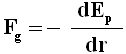
Integrando la precedente otteniamo proprio la (4.1). Aggiungiamo il fatto che si dicono superfici equipotenziali quelle formate dai punti nei quali si misura la stessa energia potenziale. Nel caso del campo gravitazionale in grande, le superfici equipotenziali sono evidentemente delle superfici sferiche, giacché l'energia potenziale è funzione della distanza dalla massa che genera il campo, e i punti di una superficie sferica sono a distanza costante dal centro. Invece, nel caso del campo gravitazionale in piccolo, l'energia è costante se la quota è costante, e dunque le superfici equipotenziali sono dei piani orizzontali.
Non è difficile rendersi conto che le superfici equipotenziali sono in ogni punto perpendicolari alle linee di campo. Siano infatti due punti A e B che giacciono in una stessa superficie equipotenziale. Il lavoro per muoversi da A a B dentro la superficie equipotenziale è manifestamente nullo, poiché in A e in B la massa possiede la stessa energia potenziale, ed L = – ΔEPg. Ma il lavoro è dato dal prodotto scalare tra la forza e lo spostamento, ed esso è pari al prodotto dello spostamento per la forza per il coseno dell'angolo tra di essi compreso. Se però forza e spostamento non sono nulli, come nel nostro caso, il lavoro può essere nullo solo se è nullo il coseno del detto angolo, cioè se l'angolo tra lo spostamento (che giace nella superficie) e la forza (diretta come la linea di campo) è retto. Conclusione: le linee di campo sono ortogonali alle superfici equipotenziali, come si può verificare in tutti i casi da noi finora presi in considerazione!
.
4.2 L'energia potenziale effettiva
A partire da quanto or ora ricavato, è possibile usare le Leggi della Dinamica per conoscere qual è il tipo di moto di una massa immersa nel campo gravitazionale di un'altra massa. Allo scopo, sfrutteremo la conservazione dell'energia e del momento angolare:
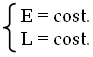
Tanto per cominciare, si ha:
dove, come si vede in figura qui sotto, vt è la componente trasversale della velocità (il prodotto vettoriale elimina la componente longitudinale e lascia la sola componente trasversale).
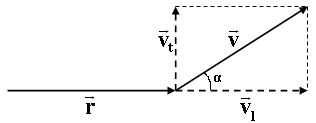
Ora, la componente trasversale è quella perpendicolare al moto. Chiamando θ l'angolo spazzato dal vettore posizione (e quindi l'angolo di rotazione), avremo:
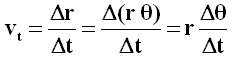
Sostituendolo nella (4.2), otteniamo:
Noi sappiamo che nel moto planetario si ha L = costante, per cui, al crescere di r, decresce la velocità angolare rappresentata dal termine Δθ/Δt (più un pianeta è lontano dal Sole, più lentamente si muove). Passiamo ora all'energia. L'espressione dell'energia cinetica è:
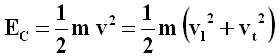
Ora, la componente longitudinale è la variazione nel tempo della posizione in direzione radiale, cioè Δr/Δt, mentre la componente trasversale è stata ricavata qui sopra. Sostituendo nella precedente si ha perciò:
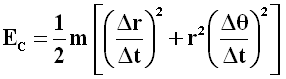
Ora, dalla (4.3) ricaviamo:
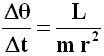
Di conseguenza:
Il termine L2/2 m r2 si dice energia potenziale centrifuga. Si noti la sparizione del termine θ(t)! La (4.1) e la (4.4) permettono di ricavare l'energia meccanica totale del pianeta in questione:
Osserviamo che il primo termine della (4.5) è un'energia cinetica come la si intende di solito. Introduciamo perciò una nuova grandezza, chiamata energia potenziale effettiva EPeff:
La (4.5) perciò diventa:
In tal modo, l'energia viene a dipendere da una sola variabile, la distanza r dalla massa M che genera il campo! L infatti è costante per ogni orbita. È evidente che l'energia totale si conserva, dunque al crescere dell'energia cinetica diminuisce l'energia potenziale effettiva, e viceversa. Attenzione, perchè proprio la (4.7) ci permetterà di descrivere i possibili tipi di moto del nostro corpo!
Rappresentiamo infatti l'andamento dell'energia potenziale effettiva (4.6). Essa è data dalla somma di due termini, uno dei quali va come 1/r2, l'altro come – 1/r. Il primo domina manifestamente sul secondo, e perciò, per r che tende a zero, EPeff tende all'infinito. L'energia potenziale gravitazionale (negativa) domina per valori intermedi, poi la funzione si appiattisce a zero dalla parte dei valori negativi.
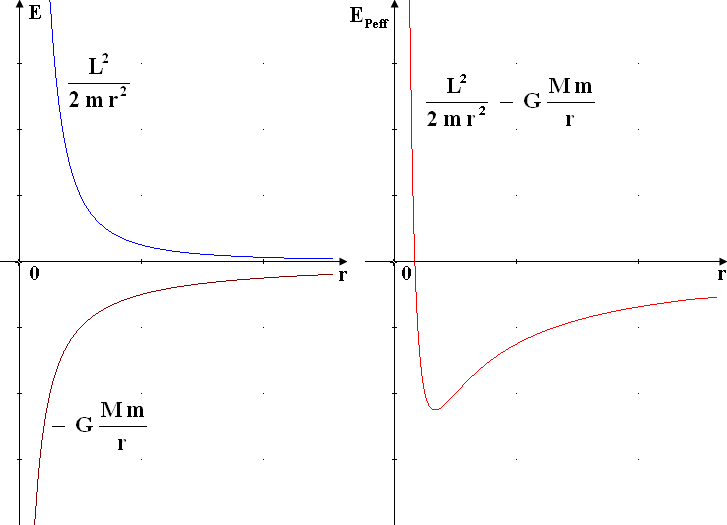
Per la (4.5), l'energia cinetica EC è data dalla differenza tra l'energia meccanica totale e l'energia potenziale effettiva. Ma, come si sa, l'energia cinetica non può mai essere negativa: o è nulla, e allora il corpo si trova in quiete, o è positiva, e allora il corpo si muove. Di conseguenza, il pianeta può muoversi solo se risulta:
![]()
Questo limita i possibili moti del pianeta in modo drastico!
4.3 La Prima Legge di Kepler riveduta e corretta
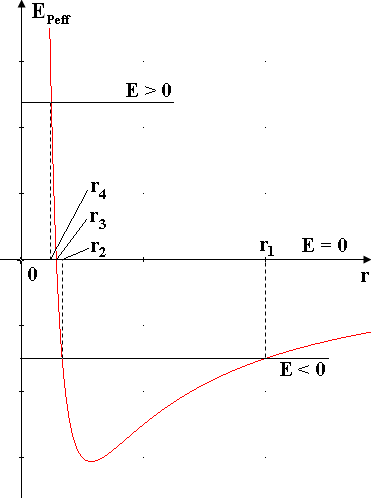
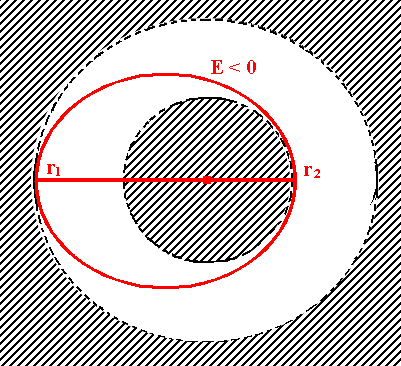
Tagliamo infatti la curva dell'Energia potenziale efficace disegnata qui sopra con un livello di energia totale minore di zero (E < 0). Il pianeta in questo caso si trova dentro quella che viene chiamata una buca di potenziale, e può muoversi solo se la sua energia potenziale effettiva è minore di E, cioè non può avvicinarsi alla massa centrale più di r2 e non può allontanarsene più di r1, come si vede qui sotto! Ciò significa che il suo moto avviene dentro una corona circolare di raggi r1 ed r2, esso non può raggiungere l'infinito, e di conseguenza la traiettoria è giocoforza una curva limitata. Se in particolare r = r1 ed r = r2, si ha E = EPeff, e quindi EC = 0. Ciò non significa che il pianeta è fermo, ma che la componente radiale della velocità è nulla in questi punti: il moto del pianeta non avviene cioè in direzione radiale, bensì tangente alla sua congiungente con il Sole. Non può che trattarsi di un'ellisse: il sole occupa uno dei suoi fuochi, mentre r1 rappresenta la distanza dal Sole dell'afelio, ed r2 quella del perielio. E così ritroviamo la Prima Legge di Keplero!
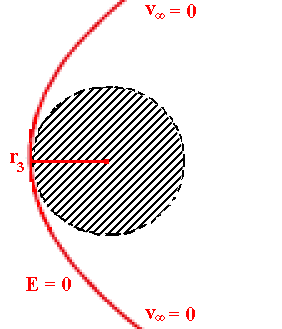
Se tagliamo il grafico dell'energia potenziale effettiva con il livello di energia totale E = 0, scopriremo che una delle due intersezioni con la curva va all'infinito, per cui il pianeta potrà muoversi da r3 fino all'infinito, cioè al di fuori di una circonferenza di raggio r3! La traiettoria non è chiusa, perchè il pianeta ha abbastanza energia per arrivare fino all'infinito; però ci arriva con energia totale nulla, e siccome lì anche EPeff = 0, se ne deduce che l'energia cinetica all'infinito è nulla. In altre parole, la velocità asintotica (cioè quella raggiunta lontanissimo dal Sole) è nulla! La situazione fisica in questione è quella di un corpo, inizialmente in quiete molto lontano da qualunque massa, che comincia ad avvertire l'attrazione da parte del Sole e gli si avvicina, raggiungendo il perielio per r = r3, e poi tornando ad allontanarsi, mentre la sua velocità diminuisce sempre più, fino a diventare nulla a grandissime distanze. La traiettoria viene descritta da una parabola.
Se infine tagliamo il diagramma dell' con un livello di energia totale minore di zero, si vede bene che il pianeta ha abbastanza energia per muoversi da r4 fino all'infinito. Stavolta però all'infinito ci arriva con energia cinetica maggiore di zero, e quindi con velocità asintotica non nulla. Se r tende all'infinito, nella (4.5) si ha:
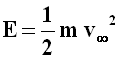
da cui:
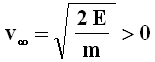
All'infinito la forza gravitazionale esercitata dal Sole è nulla, dunque il corpo celeste è uscito "fuori" dal suo campo gravitazionale. In pratica, a grandissima distanza dall'astro, è come se avessimo un corpo che si muove in linea retta con velocità v∞, cioè di moto inerziale, non avvertendo alcun influsso gravitazionale. Non appena esso avverte la forza esercitata su di esso dal Sole, la sua traiettoria è deviata dalla linea retta, ed esso si immette in un'orbita che lo porta al perielio per r = r4, e poi lo fa allontanare dal Sole, riacquistando a grandi distanze la velocità asintotica v∞. Tale traiettoria non può che essere un'iperbole!
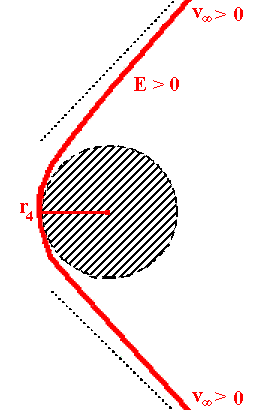
Abbiamo così scoperto che il moto ellittico non è l'unico possibile nello spazio, ma è solo quello caratteristico di un corpo orbitante con energia totale negativa. Un corpo che, fermo nello spazio con energia totale nulla, viene improvvisamente "catturato" dalla gravità solare, si muove lungo una traiettoria parabolica, mentre una cometa che giunge dalla profondità degli spazi con velocità diversa da zero si immette su una traiettoria iperbolica. La Prima Legge di Keplero è perciò un caso particolare di una legge più generale, secondo la quale la forza di gravitazione universale fa sì che i corpi si muovano lungo traiettorie rappresentate da sezioni coniche, quali sono appunto ellisse, iperbole e parabola!
Naturalmente è in agguato una vostra obiezione: l'iperbole è infatti costituita da due rami separati, come sanno tutti gli studenti di Terza Liceo:
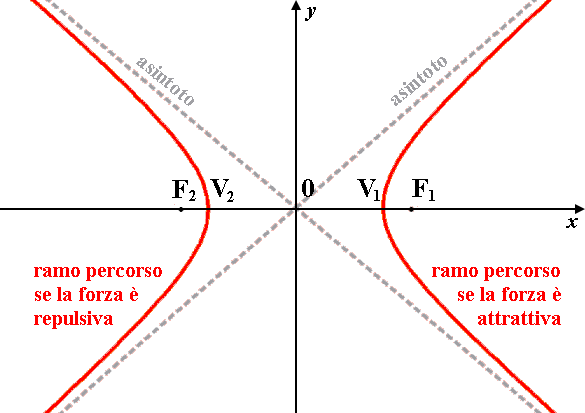
eppure, il diagramma da noi riportato qui sopra ci mostra come una cometa percorra solo uno di questi due rami. E l'altro? La risposta è molto semplice: se il Sole si trova nel fuoco F1 dell'iperbole (quello di destra, di ascissa positiva), allora il corpo celeste con energia totale positiva percorre il ramo destro della curva, curvato dall'attrazione solare. Il ramo sinistro invece, come si può dimostrare, è quello che sarebbe percorso dal corpo celeste se la forza di gravitazione fosse repulsiva, e non attrattiva! Un'eventualità che però, allo stato attuale delle nostre conoscenze, non può verificarsi.
.
4.4 Diverso momento angolare, diverse orbite
Vale la pena di approfondire il discorso prima di passare oltre; chi vuole, può saltare questo paragrafo di contenuto schiettamente matematico, e arrivare direttamente alle conclusioni. Gli studenti che hanno già acquisito i rudimenti della Geometria Analitica sanno che ellisse, parabola ed iperbole hanno ciascuna una definizione diversa dalle altre; ma è possibile dare una definizione generale di conica, senza tirare in ballo le sezioni di un cono con un piano? La risposta è affermativa:
Si dice conica di eccentricità e il luogo dei punti che hanno costante e pari ad e il rapporto delle distanze da un punto fisso detto fuoco e una retta fissa detta direttrice.
Sia d la direttrice (tratteggiata in figura) ed F1 il fuoco, e si consideri un generico punto P della conica, in questo caso per semplicità un'ellisse. Chiamiamo Q la sua proiezione sulla direttrice. La definizione sopra scritta può allora così essere espressa in termini matematici:
La retta passante per il fuoco F1 e perpendicolare alla direttrice si dice linea degli apsidi, e nella figura sottostante è stata assunta come asse x. L'ellisse interseca la linea degli apsidi in due punti A e B, detti appunto apsidi; il punto A, più vicino al fuoco e alla direttrice, si dice periapside o periastro (perielio nel caso del Sistema Solare, perigeo nel caso di satelliti rotanti intorno alla Terra), mentre il punto B si dice apoapside o apoastro (afelio nel caso del Sistema Solare, apogeo nel caso di satelliti rotanti intorno alla Terra). Chiamiamo θ l'angolo formato dal segmento PF1 con la linea degli apsidi; tale angolo è detto anomalia. Quando vale 0° ci troviamo nel periapside, quando vale 180° siamo nell'apoapside.

PF1 è la distanza del satellite dall'astro, e dunque la indicheremo con r. Chiamiamo invece d la distanza F1K del fuoco F1 dalla direttrice. Siccome F1H = r cos θ, per note proprietà della trigonometria, avremo:
PQ = HK = F1K – F1H = d – r cos θ
Perciò, sostituendo nella (4.8):
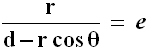
da cui si ricava con facili calcoli:
Questa è l'equazione polare della conica. Riscriviamola ora in modo da eliminare il parametro d, che rappresenta la distanza fuoco-direttrice, introducendo un parametro maggiormente usato. Introduciamo allo scopo nella precedente i valori θ = 0° e θ = 180°, corrispondenti ai due apsidi. Si ha:
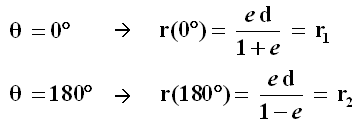
r1 si dirà la distanza perielica, r2 la distanza afelica. Sia ora 2 a la distanza AB fra i due apsidi; nel caso dell'ellisse, si tratta dell'asse maggiore. Per ottenerla, basterà sommare le due espressioni precedenti:
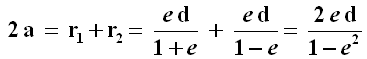
da cui e d = a (1 – e2) . Sostituendo nella (4.9) si ottiene in definitiva:
Se e = 0, si ottiene r = a cost., che è l'equazione polare di una circonferenza (distanza costante dall'origine). Usando gli strumenti dell'Analisi Matematica è possibile ricavare dalla (4.9) la variazione di r in corrispondenza di una piccola variazione di θ, che risulta:
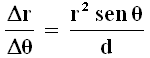
Ora, si riprenda in mano la (4.7) e da essa si ricavi il rapporto Δr/Δt:
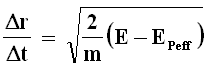
che si può agevolmente riscrivere:
In precedenza si è visto che si ha:
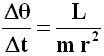
E quindi, sostituendo tutto questo nella (4.11):
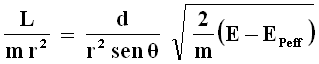
che può essere riscritta, tenendo conto della definizione di energia potenziale effettiva:
Ora, dalla (4.9) si può ricavare:
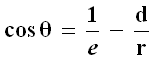
dunque, per la relazione fondamentale della trigonometria:
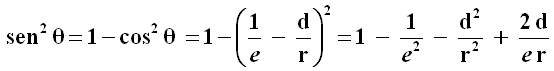
Sostituiamo tutto questo nella (4.12):
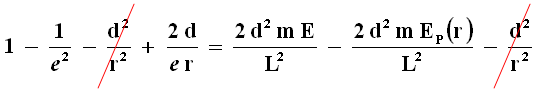
Come si vede, in tale espressione sono presenti termini costanti rispetto ad r e termini che dipendono da r. Uguagliando tra loro i termini costanti rispetto ad r otteniamo:
ed uguagliando tra loro quelli che dipendono da r:
Dalla (4.13) si ricava immediatamente l'energia totale E:
Di questa ci serviremo tra poco per un'importante deduzione. Nel caso particolare di orbite ellittiche (le uniche chiuse), si è visto che e d = a (1 – e2). La precedente può perciò così riscriversi:
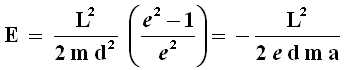
Ovvero:
Dalla (4.14) si ricava invece:
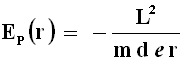
Ma ormai sappiamo bene che EP (r) = – G M m /r. Uguagliando si ha:
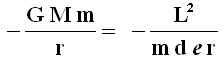
Da cui:
Confrontando fra loro la (4.16) e la (4.17) si ottiene:
Essendo G, M ed m costanti, se ne conclude che, fissato il valore dell'energia, è fissato il semiasse maggiore dell'orbita. In altre parole, tutte le orbite ellittiche con lo stesso semiasse sono caratterizzate dalla stessa energia totale, anche se hanno forme diverse!
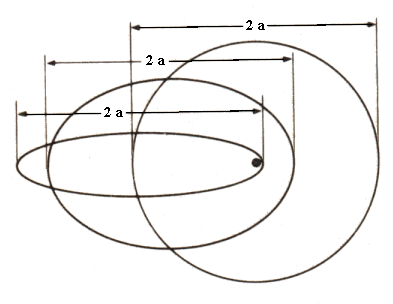
4.5 La "forma" dell'ellisse
Cosa allora determina la "forma" dell'ellisse? Ovviamente la sua eccentricità. E questa a cosa è legata? Si riprenda in mano la (4.17): siccome e d = a (1 – e2) , essa può scriversi:
![]()
Risostituendo in essa la (4.18) si ricava:
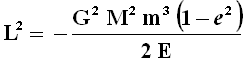
E da quest'ultima otteniamo infine:
Tutto è costante, tranne L. Ne consegue che l'eccentricità dell'orbita dipende dal momento angolare. Orbite con lo stesso asse maggiore, ma con differente eccentricità, hanno la stessa energia, ma diverso momento angolare. Ciò è assai importante: se la forza è inversamente proporzionale al quadrato della distanza, per una data energia totale si possono avere stati di moto caratterizzati da momenti angolari diversi. Ciò è molto importante anche al di fuori della nostra trattazione sulla gravitazione: infatti, quando ai primi del '900 fu elaborato il modello quantomeccanico dell'atomo, ci si rese conto che anche la forza elettrostatica con cui il nucleo attira gli elettroni dipende dall'inverso del quadrato della distanza, per cui, in ogni livello energetico, si possono avere diversi elettroni caratterizzati da diversi momenti angolari, che corrispondono a diverse eccentricità dell'orbita; venne così elaborato per la prima volta il concetto di orbitale.
È importante sottolineare che la (4.19) è vera per qualunque forma dell'orbita, non solo per quella ellittica, come potrebbe essere verificato in maniera rigorosa. E la stessa cosa vale per la (4.15). In particolare osserviamo che in quest'ultima:
a) se e
> 1, 1/e2 < 1, e quindi E > 0.
Si tratta dunque di un'iperbole.
b) se e = 1, 1/e2 = 1, e quindi E
= 0. Si tratta dunque di una parabola.
c) se e < 1, 1/e2 > 1, e quindi E
< 0, Si tratta dunque di un'ellisse.
Ritroviamo così un importante assunto della Geometria Analitica: le coniche con eccentricità maggiore di uno sono iperboli, quelle con eccentricità pari ad uno sono parabole, quelle con eccentricità minore di uno, sono ellissi. Se poi in particolare l'eccentricità è nulla, abbiamo visto che si tratta di una circonferenza. Ecco ad esempio cosa accade a un satellite se, fissato il corpo celeste intorno a cui esso ruota, io aumento gradatamente la sua energia totale: l'orbita ellittica si fa sempre più eccentrica, fino a diventare un'orbita parabolica, ed infine iperbolica, nel qual caso il corpo "lascia" il campo gravitazionale, e se ne va per conto suo!
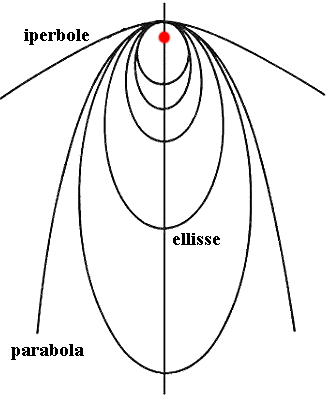
Da notare che non si conoscevano orbite iperboliche nel Sistena Solare fino al 2017, quando venne osservato il primo di una serie di oggetti interstellari, cioè di corpi celesti che provengono dallo spazio profondo e visitano temporaneamente il sistema solare percorrendo un’orbita molto aperta, per poi scomparire dalla vista dei nostri telescopi. Il 18 ottobre 2017 infatti fu scoperto 1I/'Oumuamua, un piccolo corpo celeste di forma insolita, classificato come il primo asteroide proveniente dall'esterno del Sistema Solare (I1 sta per "primo interstellare"). Il suo nome in lingua hawaiana significa "messaggero che arriva per primo da lontano". Il 30 agosto 2019 fu poi la volta della cometa iperbolica 2I/Borisov. Il terzo oggetto a mostrare una traiettoria difficilmente compatibile con un’origine all’interno del sistema solare fu 3I/ATLAS, scoperto il 1° luglio 2025 da uno studente di astrofisica della California. il suo diametro fu stmato intorno ai 20 chilometri, il che lo rende molto più grande dei suoi predecessori 'Oumuamua e Borisov, i quali misuravano solo poche centinaia di metri. E vi sono pochi dubbi che la lista degli oggetti celesti su traiettorie iperboliche sia destinata ben presto ad allungarsi.
Peraltro, sembra quasi di essere nei panni di Dante Alighieri quando, dall'alto della sfera delle stelle fisse, ha modo di "guardare giù" e di vedere tutti i pianeti allineati, rendendosi conto delle loro dimensioni, della loro velocità e della distanza fra le loro orbite:
«
Vidi la figlia di Latona [la Luna] incensa
sanza quell'ombra che mi fu cagione
per che già la credetti rara e densa.
L'aspetto del tuo nato, Iperïone [il Sole],
quivi sostenni, e vidi com'si move
circa e vicino a lui Maia e Dïone [Mercurio e Venere].
Quindi m'apparve il temperar di Giove
tra 'l padre e 'l figlio [Saturno e Marte]; e quindi mi fu chiaro
il varïar che fanno di lor dove;
e tutti e sette mi si dimostraro
quanto son grandi e quanto son veloci
e come sono in distante riparo. »
(Par. XXII, 139- 150)

La congiunzione di Venere e Giove vista dal mio giardino il 28 febbraio 2023
.
4.6 Quando Giotto dipinse la cometa di Halley
Da notare che questo discorso delle orbite, oltre ai pianeti, riguarda da vicino anche le comete. Questi affascinanti e sfuggenti corpi celesti furono a lungo ritenuti infausti: nell'arazzo di Bayeux (confezionato verso il 1070), che racconta la conquista normanna dell'Inghilterra, si afferma che l'apparizione di una cometa annunciò al re sassone Harold la prossima sconfitta ad opera di Guglielmo il Conquistatore. Gli antichi pensavano alle comete come a dei fenomeni atmosferici, ed anche il grande Galilei la pensava così. Il primo a rendersi conto che si tratta di corpi celesti fu il già citato astronomo danese Tycho Brahe (§ 1.5), e confrontando i parametri orbitali di un certo numero di comete l'inglese Edmund Halley (1656–1742) si accorse che la cometa apparsa nel 1682 nei cieli di Londra era lo stesso astro osservato nel 1607 e nel 1531, e predisse con successo il suo ritorno nel 1758, anche se egli non fece in tempo a vederla. Oggi sappiamo che la stella raffigurata da Giotto da Bondone (1267–1337) nell'"Adorazione dei Magi" nella Cappella degli Scrovegni a Padova era proprio la cometa di Halley, osservata dal pittore nel 1301; il suo ultimo passaggio risale al 1986, quando venne studiata dalle due sonde sovietiche Vega 1 e Vega 2 e dalla sonda europea Giotto. Proprio la sonda Giotto dissipò gli ultimi dubbi sulle comete, dimostrando che si tratta di corpi ghiacciati, una specie di iceberg delle dimensioni di qualche chilometro, i quali sublimano quando si avvicinano al Sole, dando vita prima a una chioma gassosa (in latino "coma", da cui "cometa"), e poi a una spettacolare coda, sempre rivolta in direzione opposta al Sole, che rende la cometa uno dei corpi celesti più affascinanti da osservare.
Studiando le loro orbite, si ritiene che le comete di corto periodo provengano dal cosiddetto disco diffuso, una zona ricca di piccoli corpi al di là dell'orbita di Nettuno, mentre si ritiene che il serbatoio delle comete a lungo periodo sia la remotissima Nube di Oort, una distribuzione sferica di materia compresa tra 0,3 e 1,5 anni luce di distanza dal Sole, che costituirebbe il confine del Sistema solare, e la cui esistenza è stata ipotizzata nel 1950 dall'astronomo olandese Jan Oort (1900–1992). Secondo lui in quell'eterna notte cosmica un gran numero di comete orbiterebbe intorno al Sole su orbite quasi circolari; occasionalmente l'influenza gravitazionale dei pianeti esterni o delle stelle vicine sposterebbe uno di questi oggetti su un'orbita fortemente ellittica, che lo porterebbe a lanciarsi verso le regioni più interne del Sistema Solare, e lì apparirebbe come una vistosa cometa. Una vecchia teoria sosteneva che il Sole ha una compagna oscura, chiamata Nemesi, che con la sua influenza gravitazionale provocherebbe lo spostamento delle comete verso il Sole, e secondo alcuni proprio il disturbo mareale provocato da Nemesi avrebbe causato periodiche piogge di comete e meteoriti sulla Terra, causando ricorrenti estinzioni di massa, l'ultima delle quali sarebbe stata l'estinzione dei dinosauri alla fine del Mesozoico (vedi in proposito il mio Ipertesto "L'Anno della Terra"). L'esistenza di questa stella vendicativa, cui Isaac Asimov dedicò un celebre romanzo, è però stata smentita da decenni di osservazioni.
Veniamo ora a discutere le possibili orbite seguite dalle comete. La maggior parte di esse segue orbite ellittiche molto allungate che le portano ad avvicinarsi al Sole per brevi periodi, per poi tornare nelle zone più lontane del Sistema Solare. Sono dette comete di corto periodo quelle che hanno un periodo orbitale inferiore ai 200 anni, per lo più percorrono orbite entro il piano dell'eclittica (quello entro il quale ruotano i pianeti), il loro afelio si trova nella regione dei pianeti gassosi. Tra queste la più famosa è proprio la Cometa di Halley, che ha un periodo 75 anni e 4 mesi, e il cui afelio si trova poco al di là dell'orbita di Nettuno. Quella con il periodo più breve conosciuto è la Cometa di Encke, scoperta nel 1819 dal tedesco Johann Franz Encke (1791–1865): ha un periodo di soli 3 anni, 3 mesi e 17 giorni, e la sua orbita non oltrepassa mai quella di Giove.

Giotto,
"L'Adorazione dei Magi", affresco della Cappella degli Scrovegni,
Padova, 1305-1305.
Sopra la capanna è visibile la cometa di Halley, il cui passaggio fu osservato
dal pittore nel 1301
.
Le comete di lungo periodo percorrono invece orbite con elevate eccentricità e con periodi superiori ai 200 anni; alcune hanno un periodo lungo milioni di anni! Le loro orbite hanno l'afelio oltre la regione dei pianeti gassosi, e il loro piano orbitale può essere assai inclinato sull'eclittica. Il record del periodo più lungo spetta per ora alla Cometa di Delevan, scoperta nel 1914, che avrebbe un periodo addirittura di 750 milioni di anni! Vi sono però anche le cosiddette comete extrasolari, le quali percorrono orbite paraboliche o iperboliche, che le portano ad uscire per sempre dal Sistema Solare dopo esser passate una volta sola in prossimità del Sole. Le comete di corto e di lungo periodo sono anche dette comete periodiche, perché percorrono un'orbita chiusa. In ogni caso, le comete periodiche sono destinate prima i poi a sparire, perché l'intensa radiazione solare le fa evaporare su tempi più o meno lunghi. Proprio il fatto che le comete continuino ad attraversare il Sistema Solare Interno portò Oort a postulare l'esistenza di un remoto serbatoio cometario (la nube di Oort), altrimenti a quest'ora il Sole le avrebbe già distrutte tutte.
Poiché le orbite percorse dalle comete le portano in prossimità dei giganti gassosi, esse sono soggette a forti perturbazioni gravitazionali, che cambiano il loro periodo di rivoluzione. Le comete di corto periodo mostrano la tendenza a sincronizzare il proprio periodo con quello di Giove, dato che questo gigante possiede una massa quasi doppia di tutti gli altri pianeti messi assieme. Queste perturbazioni possono trasferire alcune comete di lungo periodo su orbite con periodi orbitali più brevi (la Cometa di Halley ne è un esempio), ma le sue forze di marea possono essere tali da frantumarle. È quanto è accaduto alla Cometa Shoemaker-Levy, scoperta il 25 marzo 1993 dagli astronomi Eugene e Carolyn Shoemaker e dall'astrofilo David Levy, la quale fu letteralmente catturata dall'attrazione di Giove e spezzata in un treno di minuscoli frammenti i quali, tra il 16 ed il 22 luglio 1994, precipitarono nella densa atmosfera del gigante gassoso, evento reso famoso dalla copertura mediatica assicurata dai moderni mezzi di comunicazione. Del resto le sonde Voyager 1 e 2 e Galileo osservarono sui satelliti Ganimede e Callisto una serie di file rettilinee di crateri da impatto, probabilmente provocate da antiche comete schiantatesi sulle loro superfici ghiacciate.
Esiste infine una stretta relazione tra le orbite delle comete e le piogge meteoritiche che rallegrano i nostri cieli, spingendoci ingenuamente ad esprimere un desiderio quando le avvistiamo. La più famosa è quella delle Perseidi, chiamate "Lacrime di San Lorenzo" perchè tale sciame raggiunge il massimo attorno al 10 agosto, giorno in cui è commemorato questo Santo, come ricorda il poeta Giovanni Pascoli (1855-1912) in una sua celeberrima e struggente lirica, « X Agosto », facente parte della raccolta "Myricae" (1903). Fu l'astronomo italiano Giovanni Virginio Schiaparelli (1835–1910), con le sue "Note e riflessioni intorno alla teoria astronomica delle stelle cadenti" (1867), a dimostrare che le Perseidi si muovono sulla stessa orbita della cometa 1862 III, e che lo sciame delle Leonidi, visibile in novembre, segue la stessa orbita della cometa 1866 I. Ciò lo convinse che gli sciami di "stelle cadenti" siano da associare all'attraversamento da parte della Terra delle scie di detriti seminati dalle comete lungo le proprie orbite. Non sarà molto romantico, ma quasi certamente Schiaparelli aveva ragione.
.
In tutto questo, abbiamo sempre parlato di corpi celesti, e non abbiamo mai accennato né ai satelliti artificiali, messi in orbita dall'uomo, né alla velocità necessaria ad un razzo per porli in orbita. Vedremo di colmare rapidamente questa lacuna nel capitolo successivo! Per tornare all'indice, invece, cliccate qui.
![]()