![]()
|
"Par dela le
soleil, par dela les ethers, Charles Baudelaire, "Elevation" |
.
7.1 Gli Universi Isola
Come si è visto, dopo la rivoluzione operata da Copernico, da Galileo e da Newton la Terra non occupava più una posizione privilegiata nell'universo; man mano che le osservazioni progredivano, poi, si comprese che nemmeno il Sole si trovava più al centro del cosmo, ma anzi era una stella qualsiasi come molte altre. Di capitale importanza fu l'osservazione della Via Lattea, la lunga striscia brillante che attraversa il cielo, e che ebbe questo nome poiché gli antichi Greci credettero che essa fosse stata originata da una poppata di latte sfuggita alla bocca di Zeus bambino ("galaxìas" in greco significa "latteo"). Anche gli antichi Egizi davano della Via Lattea una spiegazione mitica, considerandola la controparte celeste del Nilo. Gli arabi la chiamavano "la via della paglia", i popoli turchi e ugro-finnici "la via degli uccelli", i cinesi "il Fiume d'argento", mentre in sanscrito è detta "Akasha Ganga", il "Gange celeste".
I primi a guardare alla Via Lattea con occhio scientifico furono i filosofi greci Anassagora di Clazomene (500–428 a.C.) e Democrito di Abdera (450–370 a.C.), i quali avanzarono l'idea che la Via Lattea fosse una grande massa di stelle molto distanti, e perciò invisibili ad occhio nudo. Una prima conferma giunse nel 1610, quando Galileo Galilei la osservò con il suo cannocchiale e riuscì a risolverla in un ammasso di deboli stelline. Nel 1755 lo scienziato e filosofo Immanuel Kant (1724–1804) propose che la Via Lattea fosse in realtà un corpo in rotazione formato da un numero enorme di stelle, legate dalla forza di gravità come avviene nel sistema solare, ma in scala molto maggiore; siccome noi viviamo all'interno di questo disco di stelle, lo vediamo come una lunga scia chiara solo per un effetto prospettico. Kant inoltre propose che alcune delle nebulose visibili nel cielo notturno altro non fossero che delle galassie simili alla nostra, ma molto più lontane.
Il primo tentativo di descrivere la forma della Via Lattea e la posizione del Sole al suo interno fu operato nel 1785 da William Herschel, lo scopritore di Urano, attraverso un conteggio scrupoloso del numero di stelle in seicento regioni differenti del cielo. Disegnò in seguito un diagramma della forma della Galassia, ma credette erroneamente che il Sole si trovasse nei pressi del suo centro, per cui la sua proposta appare distorta rispetto a quella che oggi sappiamo essere la forma effettiva della Via Lattea.
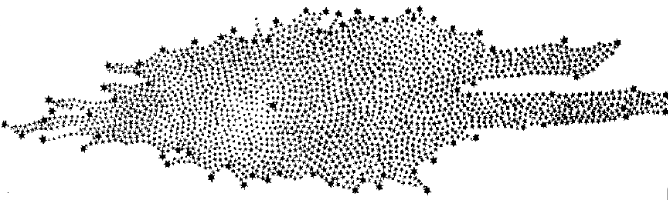
La forma della Via Lattea secondo William Herschel
Nel 1917 l'americano Heber Curtis (1872–1942) osservò la supernova S Andromedae all'interno della Grande Nebulosa di Andromeda, e studiando altre altre undici Novae apparse in esse si accorse che la magnitudine apparente di questi oggetti era stata 10 volte inferiore di quella che raggiungono gli oggetti simili all'interno della Via Lattea. Come risultato egli calcolò che la nebulosa di Andromeda dovesse trovarsi ad una distanza di circa 500.000 anni luce dalla Terra, dunque fuori dalla Via Lattea. Non poteva trattarsi di una nube di gas interstellare, come si pensava allora. Formulò così la teoria degli "universi isola", secondo la quale le nebulose di forma a spirale sono in realtà galassie separate simili alla nostra.
Non tutti accettarono questa nuova visione del cosmo. Il problema fu però definitivamente risolto nei primi anni venti dall'americano Edwin Hubble (1889–1953), soprannominato "il Titano dell'Astronomia", che si servì del potente telescopio Hooker da 100 pollici, appena costruito nell'osservatorio di Monte Wilson vicino a Pasadena (California). Grazie alla potenza di questo strumento, nel 1929 Hubble fu in grado di risolvere le parti esterne di alcune nebulose spiraliformi come insiemi di stelle. Ma soprattutto, egli ideò un metodo geniale per la misura delle distanze di queste stelle: il cosiddetto red shift, lo spostamento verso il rosso delle righe spettrali nella luce di quelle galassie.
Come aveva evidenziato per primo il fisico viennese Christian Andreas Doppler (1803–1853), se una sorgente di onde si muove di moto relativo rispetto ad un osservatore fermo, quest'ultimo percepirà una frequenza maggiore mentre la sorgente si avvicina, e minore quando essa si allontana. Come si vede nella figura sottostante, infatti, l'onda risulterà compressa nella direzione del moto, e quindi con lunghezza d'onda minore e frequenza maggiore, e dilatata nella direzione opposta, e quindi con lunghezza d'onda maggiore e frequenza minore. Ciò spiega perchè il fischio della sirena di un'ambulanza appare assai più acuto (frequenza maggiore) mentre essa si avvicina a noi, e più grave (frequenza minore) quando ci ha ormai superato e si allontana. Tale fenomeno prende il nome di effetto Doppler.

Lo stesso fenomeno vale anche per la luce, che altro non è se non un'onda elettromagnetica. Se la sorgente si avvicina a noi con velocità comparabile con quella della luce, noi vedremo la frequenza aumentare, e quindi i colori tendere al blu; se invece si allontana da noi, vedremo la frequenza diminuire, e i colori tenderanno al rosso. Ora, Edwin Hubble osservò gli spettri della luce di varie galassie, e le vide tutte più rosse di quanto si aspettava: le righe spettrali erano tutte spostate verso il rosso (da qui il nome di "red shift"). Ecco alcuni esempi di osservazioni da lui stesso effettuate:
|
Galassia
nella |
velocità: |
distanza: |
|
VERGINE
|
120 Km/s |
4 x 107 a.l. |
|
|
||
|
ORSA MAGGIORE
|
15.000 Km/s |
6 x 108 a.l. |
|
|
||
|
CORONA BOREALE
|
21.600 Km/s |
8 x 108 a.l. |
|
|
||
|
BOOTE
|
39.200 Km/s |
1,8 x 109 a.l. |
|
|
||
|
IDRA
|
60.800 Km/s |
2,6 x 109 a.l. |
|
|
||
.
7.2 L'universo si espande
Dallo spostamento delle righe spettrali è possibile risalire alla velocità delle galassie, alcune delle quali risultarono allontanarsi da noi ad una frazione apprezzabile della velocità della luce, come si vede nella tabella soprastante. La grande sorpresa fu che tutte le galassie stanno allontanandosi da noi ad alta velocità.
Osservando poi le variabili cefeidi in queste galassie, Hubble potè stimare la loro distanza da noi: come scoperto nel 1907 da Henrietta Leavitt (1868-1921), astronoma dell'università di Harvard, il periodo della variazione di luminosità di tali stelle (la prima delle quali fu scoperta nella costellazione di Cefeo, da cui il nome) è direttamente proporzionale alla loro magnitudine assoluta; misurando la magnitudine apparente e confrontandola con quest'ultima, è possibile risalire alla loro distanza da noi.
Confrontando la velocità v di regressione delle galassie da noi con la loro distanza r, desunta dal metodo delle cefeidi, nel 1929 Hubble compì una scoperta eclatante: tale velocità è direttamente proporzionale alla distanza, come mostra il diagramma, desunto dalla tabella di cui sopra:

Inizialmente questa venne chiamata Legge di Hubble, ma in seguito si riconobbe che essa era già stata concepita e ricavata nel 1927 dallo scienziato e gesuita belga padre Georges Lemaître (1894–1966), con gli stessi valori numerici. Lo stesso padre Lemaître, tuttavia, che aveva pubblicato i suoi risultati in lingua francese, nella traduzione del suo articolo in inglese da lui eseguita nel 1931 decise di omettere proprio la deduzione di tale legge, ritenendo le sue ricerche superate da quelle di Hubble di due anni prima. Una modestia davvero d'altri tempi, che fu premiata dagli astrofisici di tutto il mondo nell'assemblea generale dell'Unione Astronomica Internazionale, riunitasi a Vienna il 29 agosto 2018, riconoscendo finalmente pari paternità all'astrofisico belga. Da allora si parla universalmente di Legge di Hubble-Lemaître. Essa può essere analiticamente così espressa:
v = H r (7.1)
dove H è chiamata la costante di Hubble-Lemaître . Si tratta della più importante costante della cosmologia, e per comprenderne il significato basta supporre che il moto di allontanamento delle galassie sia rettilineo uniforme. Allora, per note leggi della cinematica.
r = r0 + v t
dove r0 è la posizione iniziale delle galassie. Sostituendo nella legge di Hubble-Lemaître (7.1) si ha:
v = H r = H (r0 + v t)
cioè:
v = H r0 + (H t) v
Ora, per il principio d'identità dei polinomi si ha v = v solo se r0 = 0 ed H t = 1.
r0 = 0 significa che, all'istante zero, tutte le galassie erano concentrate in un solo punto. Quanto tempo fa ciò avvenne? Lo si calcola mediante la seconda equazione:

Per valutare l'età dell'universo occorre conoscere il valore H della Costante di Hubble-Lemaître; lo stesso Hubble aveva proposto un valore di 50 Km/s per Megaparsec (cioè per ogni milione di parsec). Da qui si ricaverebbe:

cioè circa 20 miliardi di anni. Ben presto ci si accorse però che la stima di Hubble era troppo alta, e così venne rivista al ribasso. Dopo sette anni di misurazioni il satellite NASA WMAP (Wilkinson Microwave Anisotropy Probe) ha fornito una stima di H = (71,0 ± 2,5) km/s per Megaparsec, risultato pubblicato nel 2010 che fornisce un'età dell'universo pari a (13,7 ± 0,3) miliardi di anni.
Per fare un esempio di applicazione della (7.1): una galassia per la quale è misurata una velocità di 2000 Km/s dista dalla Terra circa:

cioè (91,00 ± 3,3) milioni di anni luce. L'errore assoluto è stato ricavato in base alla regola secondo cui l'errore relativo del rapporto di due grandezze è pari alla somma dei rispettivi errori relativi.
.
7.3 Perchè il cielo di notte è buio?
Lemaître ed Hubble dimostrarono in tal modo l'espansione dell'universo. Naturalmente emerse subito un'obiezione: se le galassie si stanno tutte allontanando da noi, vuol dire che la Terra occupa una posizione privilegiata, al centro dell'universo? La risposta è no. Si consideri infatti un palloncino sul quale sono depositate delle coccinelle. Gonfiando il palloncino, le coccinelle si allontanano le une dalle altre, e a ciascuna sembra di essere al centro dell'espansione, perchè sulla superficie del palloncino ognuna vede le altre coccinelle allontanarsi tutte da sé, come mostra il disegno sottostante.

Oggi si pensa che parte di questo spostamento verso il rosso sia dovuto, almeno in parte, anche a cause diverse dall'espansione del cosmo. Infatti, anche la Terra é in moto all'interno della Via Lattea, per via della rotazione di questa attorno al proprio asse con un periodo di circa 220 milioni di anni. Il fatto che alcune galassie presentino uno spostamento verso il violetto sembra confermare quest'ipotesi, indicando che il loro moto relativo é diretto verso la Terra, nel senso che la Terra si muove nella Via Lattea verso di loro più rapidamente di quanto esse non si allontanino da lei. Inoltre, le Galassie hanno una massa enorme, e quindi in grado di influenzare, come spiegato nel § 6.5, la lunghezza d'onda delle radiazioni da esse rilasciate; di questo oggi si comincia a tenere conto, ma senza che la validità dell'espansione dell'universo venga inficiata.
In realtà, che l'universo si espandesse era già stato ipotizzato da tempo. La prima argomentazione contro un universo statico risale allo stesso Newton: se tutte le stelle fossero immobili nello spazio, dovrebbero attirarsi tra di loro per via della gravitazione universale, e finirebbero per collassare le une sulle altre: un universo statico, insomma, è instabile. Questo concetto è stato ben espresso anche dal già citato Immanuel Kant:
« Se l'attrazione agisce sola, tutte le parti della materia dovrebbero avvicinarsi sempre più, e diminuirebbe lo spazio che occupano le parti unite, di modo che si riunirebbero finalmente in un solo punto matematico. » ("Geografia fisica di Immanuel Kant", Tipografia di Giovanni Silvestri, Milano, 1811)
Una prima solida prova a favore dell'universo in espansione fu portata dall'astrofilo tedesco Heinrich Wilhelm Olbers (1758–1840, lo scopritore degli asteroidi Pallade e Vesta, rispettivamente nel 1802 e nel 1807. Questi si pose una domanda solo a prima vista ovvia: perchè di notte il cielo appare buio? In un articolo del 1826, Olbers propose che il cielo notturno dovrebbe piuttosto essere luminoso quanto e più del cielo diurno.
In base alle conoscenze del suo tempo, Olbers immaginò le stelle uniformemente distribuite in un universo omogeneo ed isotropo. Pensiamo dunque ad un cono con il vertice sulla Terra e diretto verso il cielo, ed intersechiamolo con due superfici sferiche centrate sempre sulla Terra e di raggi molto vicini tra loro; esse ed il cono delimitano uno strato di spessore s piccolo e di superficie A. Ipotizziamo che in esso ci siano N stelle. Consideriamo ora una sezione analoga del cono, ma a distanza doppia dalla Terra: stavolta l'area sarà 4A e quindi il volume sarà quadruplo del precedente; sempre ipotizzato l'universo omogeneo, in questo nuovo strato di stelle ce ne saranno 4 N. Ma la luminosità decresce con l'inverso del quadrato della distanza, quindi la luminosità del secondo strato sarà pari a un quarto del primo. Considerando che contiene il quadruplo delle stelle, se ne conclude che i due strati avranno la stessa luminosità. Anche considerando una terza sezione a distanza tripla, una quarta a distanza quadrupla, eccetera, tutti gli strati avranno la medesima luminosità. Se il cosmo è infinito, vi saranno infinite sezioni possibili, e quindi qualunque sezione dovrebbe apparire uniformemente luminosa: in pratica, lungo ogni direzione di vista i miei occhi dovrebbero intercettare almeno una stella. Di conseguenza tutto il cielo dovrebbe apparire come la superficie luminosa di un unico grande Sole, e il cielo notturno dovrebbe essere luminoso quanto quello diurno!
Queste considerazioni sono passate alla storia come il paradosso di Olbers. Il suo stesso autore cercò di metterci una pezza, supponendo che lo spazio sia saturo di nubi di gas le quali intercetterebbero la luce degli astri retrostanti. Se però ciò fosse vero, poiché l'energia non può andare distrutta, la luce delle stelle più lontane surriscalderebbe le nubi di gas fino a renderle incandescenti, e dunque non è possibile alcun effetto schermo. La soluzione di questo imbarazzante paradosso fu ottenuta solo dopo le scoperte di Lemaître e di Hubble. Infatti, in seguito all'espansione dell'universo, il red shift delle righe spettrali riduce l'effettiva energia raggiante ricevuta dalla Terra. La frequenza f della luce infatti diminuisce quanto più le stelle sono lontane e veloci, e diminuendo la frequenza diminuisce anche l'energia E = h f dei fotoni. Inoltre, ci viene in aiuto la Relatività di Einstein: la scala temporale all'opera sulla Terra è infatti diversa da quella solidale con le stelle, in moto rispetto a noi ad alta velocità, e quindi la quantità di luce emessa da una stella in un dato intervallo di tempo viene ricevuta dalla Terra in un intervallo più lungo se confrontato con l'orologio solidale con la stella considerata. In conclusione: l'oscurità della notte può essere spiegata solo considerando un universo in espansione.
.
7.4 Il Grande Scoppio
Naturalmente si impone una domanda: cosa può avere originato l'espansione dell'universo? Perché le Galassie si allontanano tutte l'una dall'altra, e quindi anche dalla nostra? La prima ipotesi al riguardo, che le teorie più attendibili prendono oggi a fondamento, sostiene che in principio vi fu un'esplosione primordiale, detta Big Bang ("grande scoppio"), che scagliò in ogni parte del cosmo grumi di materia, sviluppatisi poi in galassie. Il Big Bang diede origine al tempo, dunque non avrebbe senso chiedersi "cosa c'era prima del Big Bang", non essendoci stato un "prima"; e con esso non prese il via solo la corsa delle galassie ad allontanarsi l'una dall'altra, ma cominciò ad esistere lo spazio stesso nel quale le galassie esistevano. Quest'ipotesi affascinante fu formulata per la prima volta dal già citato padre Georges Lemaître (1894–1966), quindi perfezionata dal fisico ucraino George Gamow (1904–1968), fuggito negli USA per sfuggire alle purghe staliniane.
Le misure non precise della costante di Hubble-Lemaître, tuttavia, fecero pensare a più di uno che l'universo non avesse più di 11 miliardi di anni di età, mentre ad alcune remotissime galassie era assegnata un'età di quasi 15 miliardi di anni. Come poteva l'universo essere più giovane delle sue stelle più antiche? Per questo alcuni fisici rigettarono la teoria del Big Bang, e nel 1948 Hermann Bondi (1919–2005) e Fred Hoyle (1915–2001) proposero la Teoria Stazionaria, secondo la quale l'universo è sempre esistito, sempre esisterà e la sua densità è costante nel tempo. Essendo già accertata l'espansione cosmica, e quindi la riduzione del numero di atomi per unità di volume, Bondi e Hoyle proposero che nel vuoto si creasse spontaneamente nuova materia per mantenere costante la densità dell'universo. Secondo Hoyle, per mantenere costante quest'ultima compensando l'espansione basterebbe che si formasse un solo atomo di idrogeno per centimetro cubo di spazio ogni 100.000 miliardi di anni. Purtroppo per Bondi ed Hoyle, nessuna teoria fisica oggi nota giustifica la creazione di materia dal nulla, seppure con un ritmo così ridotto.
Il 28 marzo 1949 Hoyle, che era anche un noto divulgatore scientifico, tenne un intervento radiofonico al Third Programme della BBC, in cui mise in contrasto le due ipotesi sull'origine dell'universo, e tra l'altro parlò dell'« ipotesi che tutta la materia dell'universo fosse stata creata in un unico Big Bang in un momento particolare del passato remoto. » Questa conferenza fu al'origine del termine "Big Bang", e Hoyle la citò nel suo saggio "La natura dell'universo" del 1950. A volte si dice che Hoyle abbia usato quel termine in senso dispregiativo, per ridicolizzare l'ipotesi di Lemaître e di Gamow, ma non è andata così. Anche se Hoyle respinse con decisione fino alla morte l'idea di un'origine improvvisa dell'universo, in seguito affermò di non averla mai intesa come uno scherno, e del resto nessuno dei cosmologi favorevoli all'idea dell'esplosione primigenia, a partire da Lemaître e Gamow, si è mai sentito offeso da questo termine. Hoyle spiegò in seguito che aveva bisogno di metafore visive nelle sue trasmissioni per far capire al pubblico i punti più controversi dall'astrofisica, e la scelta del termine "Big Bang" era una di queste. Tra i primi che hanno usato questo termine per significare l'origine dell'universo c'è il filosofo statunitense Norwood Russell Hanson (1924-1967), che chiamava "immagine disneyoide" quella dell'esplosione cosmica. Si dovette attendere fino al marzo 1966 affinché il nome comparisse in un articolo di ricerca di "Nature", ma già negli anni ottanta il termine si era ormai radicato nella letteratura e nel linguaggio comune. L'espressione è stata adottata in molte lingue diverse dall'inglese, tra cui l'italiano, il francese ("théorie du Big Bang") e lo svedese ("Big Bang teorin"), mentre in tedesco si usa il termine Urknall, che significa "il botto originale", stesso significato della parola olandese oerknal.
La prova decisiva a favore della Teoria del Big Bang arrivò nel 1965, ad opera di Arno Penzias (1933–) e Robert Wilson (1936–), ricercatori della Bell Telephone. Mentre stavano provando un nuovo tipo di antenna per microonde, essi scoprirono una sorta di "rumore di fondo" che sembrava provenire da ogni parte dell'universo. In seguito, grazie al contributo di Robert Dicke (1916–1997) della Princeton University, essi compresero di aver captato una radiazione di corpo nero alla temperatura di 2,7 K (oltre 270° sotto lo zero centigrado), che corrisponde alla temperatura media generale dell'universo (perciò, a meno che qualche civiltà extraterrestre non abbia ottenuto risultati migliori dei nostri, le temperature prossime allo zero assoluto da noi raggiunte in laboratorio sono da considerarsi un... record universale!). Questa radiazione venne chiamata radiazione di fondo, e rappresenta l'ultima traccia della colossale "bruciatura" dovuta al Big Bang, come l'odore cattivo che permane in una stanza dopo che l'arrosto è bruciato. Per questa scoperta Penzias e Wilson ricevettero il Premio Nobel per la Fisica nel 1978.
Come mai la radiazione di microonde scoperta dal duo Penzias & Wilson può essere considerata come la prova decisiva a favore del Big Bang? Vedete, qualsiasi corpo che si trovi a una temperatura superiore allo zero assoluto emette sempre radiazioni, provocate dall'agitazione termica dei portatori di carica. In particolare, un corpo nero (ad esempio una cavità dalle pareti perfettamente opache) emette una radiazione che dipende solo dalla sua temperatura assoluta. Per la Legge di Wien, più la temperatura è elevata, più alta è la frequenza delle radiazioni. Per questo in radioastronomia ad ogni radiazione è associata una temperatura equivalente, cioè la temperatura di una cavità dentro la quale si deve porre l'antenna affinché essa registri un fascio di onde elettromagnetiche aventi un'intensità, e quindi una lunghezza d'onda, pari a quelle della radiazione ricevuta. La Legge di Wien afferma che la frequenza cui corrisponde la massima emissione di radiazioni è data da:
fMAX = α T (7.2)
dove α = 1,034 x 1011 Hz K–1 è la costante di Wien. Inserendo in essa T = 2,7 K si ottiene per fMAX un valore di 2,79 x 1011 Hz, cui corrisponde una frequenza λMAX = 10–3 m, che ricade appunto nell'intervallo delle microonde, e corrisponde al valore misurato da Penzias e Wilson con la loro antenna. La temperatura di 2,7 K corrisponde esattamente a quella prevista teoricamente per la radiazione residua della prima fase caldissima dell'universo primordiale, subito dopo il grande scoppio; dopo 13 miliardi e mezzo di anni, infatti, lo spostamento Doppler verso il rosso ha talmente indebolito la radiazione di fondo, da portarla nel freddo intervallo delle microonde. Questa tenue radiazione fossile è in parte responsabile del disturbo visibile su un comune televisore in un canale non sintonizzato, ed oggi comprende ormai solo pochi fotoni per millimetro quadrato. Per studiare nei dettagli questa radiazione è stata approntata una missione spaziale ad hoc: il satellite COBE (COsmic Background Explorer), lanciato dalla NASA il 18 novembre 1989, misurò lo spettro della radiazione cosmica di fondo a microonde, e cercare eventuali disuniformità in questa radiazione, che apparentemente sembrava omogenea in ogni direzione del cielo. La missione fu un completo successo: dopo aver misurato che la radiazione di fondo corrisponde ad uno spettro di corpo nero ad una temperatura di 2,726 K, in perfetto accordo con le previsioni teoriche), esso ha rivelato per la prima volta piccole variazioni spaziali dell'emissione, comprese fra lo 0,0001% e lo 0,001% del valore medio. I due principali ideatori e realizzatori di COBE, John C. Mather (1946-) e George F. Smoot (1945-), hanno ricevuto il Premio Nobel per la Fisica del 2006 per i risultati conseguiti dal loro satellite. Misure ancora più precise sono state ottenute dall'esperimento BOOMERanG (di cui riparleremo tra poco), che ha sfruttato tre voli suborbitali di un pallone sonda ad alta quota nel corso del 1997; il satellite WMAP, lanciato il 30 giugno 2001 e già citato in precedenza; e il satellite dell'ESA Planck, lanciato dalla Guyana francese il 14 maggio 2009.
In
aggiunta a tutte queste scoperte sulla radiazione cosmica di fondo, il
satellite Hipparcos (High Precision Parallax Collecting Satellite)
dell'ESA, messo in orbita da un razzo Ariane 4 il 18 agosto 1989, ha misurato
con grandissima precisione le distanze stellari, portando a rivedere le stime
sull'età di alcuni oggetti che erano parsi più vecchi dell'intero universo,
e facendo così cadere l'ultimo ostacolo alla definitiva accettazione della
Teoria del Big Bang. Oggi, cercando on line "Big Bang
Theory", di solito non si trovano riferimenti alla cosmologia, bensì
a una popolarissima sitcom statunitense, volta
a mettere alla berlina il cosiddetto mondo dei "nerd".
.
7.5 Le Sette Ere dell'Universo
In cosa sia consistito il Big Bang, non si é ancora riusciti a ricostruirlo con sufficiente precisione, e questo principalmente per le grosse lacune che rimangono nella nostra conoscenza della Fisica delle Particelle Elementari. Comunque, possiamo essere certi che non fu un vero e proprio scoppio, come quello di una bomba che va in centotrentasettemila pezzi scagliando schegge dappertutto; e questo semplicemente perché all'intorno... non vi era ancora spazio. Fu proprio il Big Bang a creare lo spazio, con l'espansione che ne seguì. E creò anche il tempo, perché, come avvertiva già Agostino d'Ippona (355-430), « il tempo può essere avvertito e misurato mentre passa »; ciò é vero nel senso che là dove non c'é né materia né energia nessun cambiamento può spontaneamente intervenire, come nell'Essere di Parmenide (VI sec.a.C.), ed é solo la presenza di energia, anche "materializzata", a far avvertire che vi é un "tempo" che può trascorrere. Questo ci spiega, in parte, l'inscindibilità fisica di spazio e tempo nel cronotopo. Aveva ragione, sempre Sant'Agostino, quando nelle sue "Confessioni" si faceva beffe di coloro che si chiedevano cosa mai facesse Dio prima della Creazione. Non faceva niente, risponde, perché Dio stesso non aveva ancora creato il tempo, e quindi non si poteva parlare di un "prima". Usando il linguaggio della Fisica Moderna, non si può parlare di un "prima del Big Bang", perché é stato il Big Bang stesso a generare il prima ed il dopo. Qualcuno comunque ha cominciato a porsi delle domande circa la possibile causa che ha scatenato il Big Bang, e di questo parleremo più avanti.
Tuttavia, gli studi proseguono di pari passo con l'evolversi della fisica del piccolissimo. Mediante i maggiori acceleratori di particelle del pianeta Terra, come l'LHC (Large Hadron Collider) del CERN di Ginevra, gli scienziati stanno cercando di ricostruire nei dettagli le stesse condizioni esistenti nei primissimi istanti di vita dell'universo, che era regolato da una Fisica completamente diversa da quella cui noi siamo abituati. A titolo di esempio, nel marzo 2000 un gruppo di Fisici dell'Heavy Ion Programme del CERN è riuscito, facendo collidere tra loro nuclei di piombo accelerati fin quasi alla velocità della luce (precisamente con un'energia di 33 TeraelettronVolt), a ricreare uno stato esotico della materia, chiamato "plasma di quark e gluoni", una specie di "brodo primordiale" nel quale i costituenti più intimi della materia esistevano liberi, prima che nascessero non solo gli atomi, ma anche i protoni e i neutroni. Questo plasma raggiunse una temperatura centomila volte superiore a quella esistente nel nucleo del Sole, ed è sopravvissuto per soli 10–23 secondi.
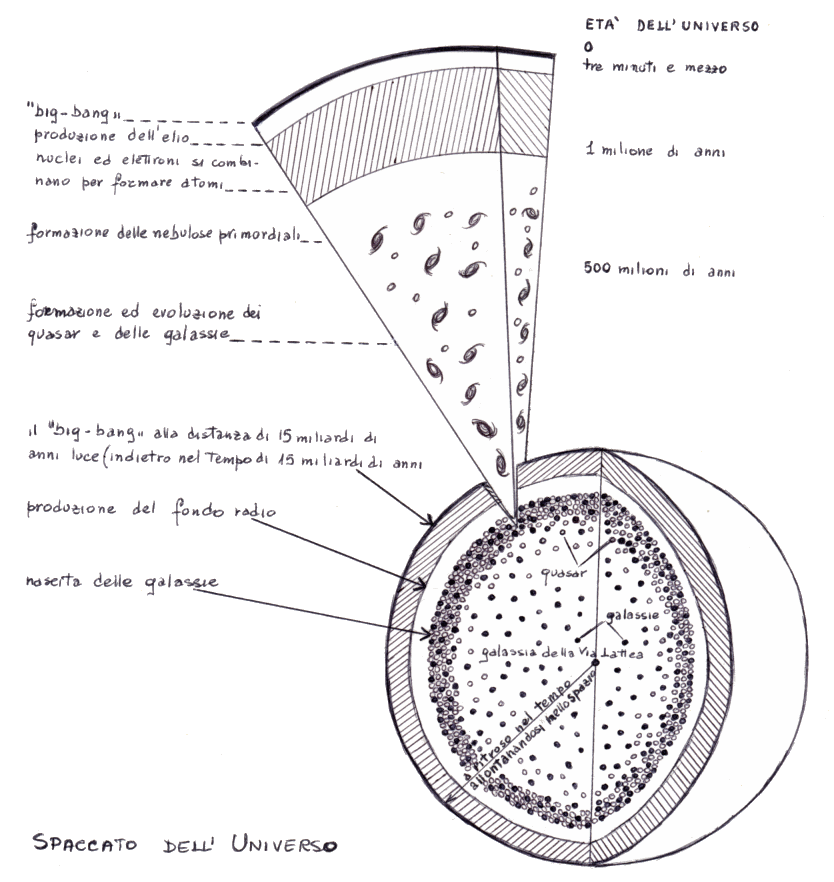
A ritroso nel tempo fino al Big Bang (disegno di Enrica Soldavini)
La storia dell'universo primordiale è stata perciò divisa in epoche, ciascuna caratterizzata da un diverso stato della materia; il passaggio da un'epoca a quella successiva è caratterizzata da una "transizione di fase", che rappresenta una totale riorganizzazione della materia e dell'energia. Le principali epoche finora individuate sono le seguenti:
1) Era di Planck
Essa parte all'istante zero e dura un "tempo di Planck", grandezza caratteristica della Meccanica Quantistica e definita a partire da tre costanti fondamentali, come vedremo nel § 8.7:
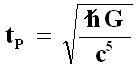
dove h tagliato è la costante di Planck ridotta h / 2π , G è la costante di gravitazione universale e c è la velocità della luce. Si dimostra che essa ha le dimensioni di un tempo e vale 5,391 x 10–44 secondi; è il "quanto di tempo", cioè il tempo più breve di cui abbia senso parlare in Fisica. Quest'era era caratterizzata dalla cosiddetta "gravità quantistica", una Fisica di cui sappiamo ancora pochissimo, e sulla quale torneremo nel prossimo capitolo. Non possedendo ancora una teoria quantistica coerente della gravitazione, per ora quest'epoca è una "terra di nessuno" che nessuno riesce a descrivere compiutamente. L'unica cosa certa è che in quest'epoca tutte le interazioni fondamentali, compresa quella gravitazionale che è l'oggetto delle nostre ricerche, erano riunite in un'unica forza originaria; probabilmente lo spazio e il tempo come noi li intendiamo non esistevano ancora.
2) Era delle GUT
Essa parte dal tempo di Planck ed arriva fino a 10–34 secondi; è caratterizzata da energie dell'ordine di 1015 GigaelettronVolt (un elettronVolt è l'energia necessaria per far spostare la carica di un elettrone nella differenza di potenziale di un Volt) e da temperature dell'ordine dei 1040 Kelvin. La transizione di fase con l'era di Planck porta la gravità a separarsi dalle altre forze, che invece sono riunite in un'unica protoforza regolata dalle cosiddette GUT (Grand Unified Theories), tuttora in discussione nell'ambito accademico (vedi § 8.1). Le primissime particelle elementari e l'intensissima radiazione sono ancora accoppiate tra di loro in un miscuglio inestricabile di materia e di energia; i fotoni, appena emessi, vengono immediatamente riassorbiti, ed i neutrini sono in equilibrio termico con le altre componenti di questo indifferenziato brodo primordiale.
3) Era elettrodebole
Comincia 10–34 secondi dopo il Big Bang ed arriva fino a 10–10 secondi. Finita l'epoca della Grande Unificazione, la forza nucleare forte (responsabile della coesione tra i nuclei) si separa dalle altre, mentre la forza nucleare debole (responsabile della radioattività) e la forza elettromagnetica restano ancora unite nell'unica forza elettrodebole. A causa di una lievissima asimmetria, si rompe l'equilibrio tra materia ed antimateria, particelle ed antiparticelle si annichilano a vicenda, le seconde spariscono quasi completamente mentre il leggero eccesso di particelle sopravvissute porta alla generazione di tutta la materia che oggi vediamo.
4) Era delle particelle
Inizia 10–10 secondi dopo il Big Bang e giunge fino a 10–5 secondi. A causa della rapida espansione, l'energia media dell'universo scende attorno ai 100 GigaelettronVolt, corrispondente a una temperatura di 1026 Kelvin, e paragonabile ai valori energetici ottenibili nei maggiori acceleratori di particelle a nostra disposizione. Tutte e quattro le forze fondamentali si separano tra di loro, e i quark e i gluoni presenti nel plasma primordiale perdono la loro libertà d'azione, venendo confinati dentro i protoni e i neutroni.
5) Era della nucleosintesi
Va da 10–5 secondi a circa un minuto dopo il Big Bang. La temperatura si è notevolmente abbassata, fino a 109 Kelvin, anche se rimane altissima per i nostri canoni umani, ma permette ancora l'equilibrio termodinamico tra materia e radiazione. Man mano però che la temperatura diminuisce, protoni e neutroni cominciano a dare vita ai primi nuclei atomici (nucleosintesi).
6) Era dei nuclei
Essa va da un minuto a circa 300.000 anni dopo il Big Bang. Gli atomi cominciano a formarsi quando i nuclei riescono a catturare i primi elettroni. La temperatura scende fino a poche migliaia di gradi e la densità scende fino a 10–20 grammi per centimetro cubo; allora avviene una fondamentale transizione di fase in cui l'equilibrio termodinamico tra materia e radiazione si rompe, e i fotoni possono finalmente liberarsi. L'universo diventa per la prima volta trasparente: è il famoso « Sia la luce! » dei primi versetti della Genesi. A questo punto ha origine la famosa radiazione cosmica di fondo osservata da Penzias e Wilson, di cui abbiamo parlato in quel che precede. Gli astrofisici sono riusciti a scattare una formidabile foto dell'universo risalente a tale periodo, grazie al telescopio italo-americano sospeso ad un pallone aerostatico nell'ambito della missione BOOMERanG (Balloon Observation Of Millimetric Extragalactic Radiation and Geophysics), frutto di otto anni di cooperazione tra l'Università di Roma La Sapienza, diretta dal professor Paolo de Bernardis, e dal California Institute of Technology, diretto dal professor Andrew Lange:
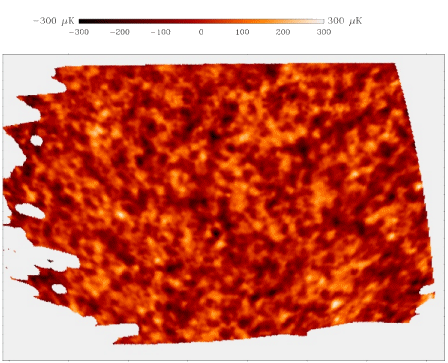
7) Era delle stelle e delle galassie
Va da 300.000 anni dopo il Big Bang fino ad oggi. La materia comincia a strutturarsi nelle forme che noi conosciamo, dando vita alle primissime stelle e alle primissime galassie. I satelliti COBE, WMAP e Planck hanno potuto misurare delle leggerissime disuniformità nella radiazione cosmica di fondo: queste piccolissime fluttuazioni primordiali, probabilmente formatesi all'inizio dell'era degli atomi, rappresentano i "semi" da cui si svilupparono i primissimi corpi celesti, dando a l'universo l'aspetto che noi ben conosciamo: da un vuoto assoluto, senza né spazio né tempo, con tutta la materia-energia concentrata in un unico punto, a temperatura e densità inimmaginabili, si é passati ad un universo punteggiato da luci e sorgenti di calore, simili alle molecole di un gas in un serbatoio, e come questo in continua espansione; un cosmo multiforme e variopinto, nel quale la materia e l'energia hanno assunto le più svariate ed incredibili configurazioni, dall'ultraimmenso all'extrapiccolo, dall'inanimato al razionale, dalle galassie alle stelle, dalle comete ai pianeti, dalla vita all'uomo.
.
7.6 L'improvviso balzo in avanti del cosmo neonato
Ormai la Teoria del Big Bang ha ricevuto così tante conferme osservative e sperimentali, che nessuno più la metterebbe seriamente in dubbio. Tuttavia, alcune incongruenze insite nella nostra Cosmologia hanno portato l'americano Alan Guth (1947–) del Massachusetts Institute of Technology e il giapponese Katsuhiko Sato (1945–) dell'Università di Tokyo a formulare nel 1981 una particolare teoria, anch'essa generalmente accettata dal mondo scientifico, riguardo a ciò che accadde tra 10–36 e 10–32 secondi dopo il Grande Scoppio. Mentre il modello classico del Big Bang propone una espansione dell'universo con ritmo pressoché costante, e comunque senza brusche variazioni, Guth e Sato proposero, indipendentemente l'uno dall'altro, che in quel breve lasso di tempo il cosmo, ancora confinato dentro una sfera di dimensioni piccolissime, abbia subito un'improvvisa espansione esponenziale, crescendo come mai aveva fatto prima e come mai avrebbe fatto più, tanto da aumentare di oltre 1030 volte le proprie dimensioni lineari.
Questo sensazionale fenomeno fu battezzato con il nome di inflazione, per analogia con l'inflazione economica, un termine inizialmente scherzoso, che poi però divenne di uso comune. Secondo Alan Guth, l'improvviso "balzo in avanti" dell'universo neonato sarebbe dovuto ad una transizione di fase, simile in certo modo a quella che subisce l'acqua quando passa allo stato di ghiaccio: quando l'acqua solidifica, da uno stato energetico più alto passa ad uno a più bassa energia. Allo stesso modo, l'inflazione sarebbe legata a una transizione dal vuoto ad alta energia ad una ad energia più bassa: l'energia del vuoto si è liberata tutta d'un colpo, tanto da far dire a Guth che « l'universo ha cominciato la sua esistenza con un pasto completamente gratuito servito dal nulla ».
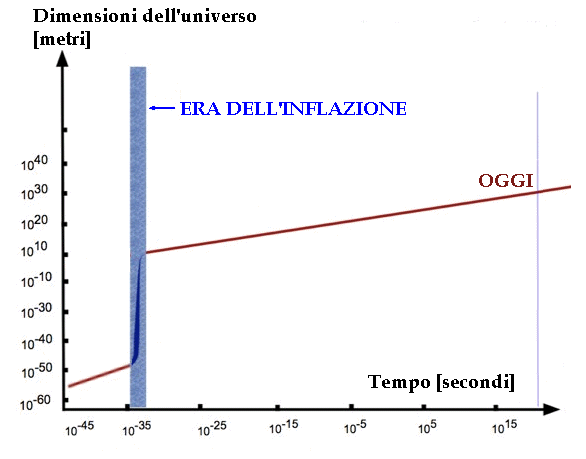
Per quanto questa teoria possa sembrare strampalata, ha il merito di risolvere moltissimi problemi legati alla teoria classica del Big Bang. Tanto per cominciare, come potevano formarsi stelle e galassie in uno spazio assolutamente omogeneo e pervaso uniformemente dalla radiazione di fondo a microonde? La teoria dell'inflazione ipotizza invece che, a seguito della violentissima espansione, le piccole fluttuazioni casuali predette dalle teorie quantistiche dei campi si siano gonfiate anch'esse in modo abnorme, dando così origine all'attuale distribuzione eterogenea della materia nello spazio. Inoltre, se l'ipotesi inflazionaria è vera, tutto l'universo osservabile si sarebbe sviluppato da una regione causalmente connessa, cioè così piccola che la luce avrebbe potuto attraversarla interamente nel brevissimo tempo intercorso fra la "nascita" dell'Universo e l'inizio dell'inflazione, e perciò avente in ogni punto le stesse caratteristiche, quali temperatura e densità; e ciò spiegherebbe perchè la stessa Fisica vale in tutti i punti del nostro universo.
Secondo alcuni Fisici Teorici, la rapidissima inflazione sarebbe stata provocata da un campo scalare chiamato inflatone, un presunto parente del campo magnetico manifestatosi nel "brodo primordiale" quando le particelle si trovavano in una situazione di altissima energia e di caos assoluto. Questo inflatone avrebbe prodotto una pressione tale da vincere l'attrazione gravitazionale, agendo come forza repulsiva e quindi come "motore" dell'inflazione; esso inoltre avrebbe generato nella materia primordiale fluttuazioni quantistiche di densità, le quali avrebbero rappresentato i "semi" per la nascita delle galassie. Il satellite WMAP ha peraltro fornito dati in ottimo accordo con la teoria inflazionaria.
Non tutti però sono d'accordo con questa teoria. Tra i critici c'è Paul Steinhardt (1952–), dell'Università di Princeton, secondo il quale tutte le simulazioni del presunto comportamento di questo inflatone danno vita a universi completamente diversi dal nostro, cioè con una densità di galassie troppo elevata rispetto a quella che noi osserviamo: solo un ristrettissimo intervallo di valori dei parametri in gioco potrebbe dar vita alla densità giusta, e ciò è giudicato troppo poco probabile affinché si fosse realizzato. Andrej Linde (1948–), della Stanford University, sostiene invece che l'inflazione, una volta innescata, non si arresterebbe affatto una frazione di secondo dopo, ma si autoalimenterebbe per mezzo di processi quantistici, dando vita a un universo molto diverso dal nostro, con infiniti universi "paralleli" nei quali ogni diversa situazione, anche la più improbabile, si può verificare; e si sa che una teoria che prevede tutto, finisce per non prevedere nulla.
Il dibattito dunque è ancora in corso: l'unico dato acquisito, per ora, è l'espansione dell'universo partita dal Big Bang. Ma questo non è l'unico aspetto controverso ed incredibile della Cosmologia degli anni duemila. Infatti nel 2023 Geraint Lewis, astrofisico dell'Università di Sydney e l'astrostatistico Brendon Brewer, dell'Università di Auckland, osservando galassie che esistevano quando l'universo aveva appena un miliardo di anni (meno di un decimo dell'età attuale), hanno visto per la prima volta il tempo scorrere a un ritmo cinque volte più lento di quanto avviene oggi, confermando un'altra previsione di Albert Einstein sugli effetti di deformazione dello spazio-tempo dovuti all'espansione dell'universo. Il concetto di rallentamento del tempo nell'universo primordiale è sorto alla fine degli anni venti del secolo scorso, quando fu scoperta l'espansione cosmica. Siccome le galassie più lontane da noi si allontanano a una velocità prossima a quella della luce, devono per forza manifestarsi effetti relativistici. Esaminando la luce di supernove esplose nelle lontane galassie primordiali, tra i sei e i sette miliardi di anni fa, gli astronomi avevano confermato la dilatazione cosmica del tempo, ma queste supernove sono troppo deboli per essere osservate alle immense distanze necessarie per sondare le epoche precedenti. Lewis e Brewer hanno tuttavia studiato oggetti molto più grandi e luminosi: i quasar, formati da buchi neri supermassicci circondati da gas che precipita in essi quasi alla velocità della luce, dove si riscalda fino a temperature di trilioni di gradi ed emette un bagliore visibile in tutto il cosmo. Purtroppo questo bagliore non è costante, perchè i buchi neri sono divoratori disordinati e incostanti, e la loro variabilità fatta di sfarfallii turbolenti rende i quasar più facili da identificare, ma ne complica l'uso come marcatori standard del tempo cosmico. Studi precedenti non erano riusciti a trovare un effetto di dilatazione temporale tra quasar molto distanti da noi e quelli relativamente vicini, tanto che alcuni avevano messo in dubbio l'idea stessa di dilatazione cosmica del tempo. Ma Lewis e Brewer hanno utilizzato una serie di dati molto ampia: 190 quasar che coprono un intervallo di tempo cosmico che va da 2,5 miliardi a 12 miliardi di anni fa, e il tremolio di ogni quasar è stato osservato centinaia di volte a diverse lunghezze d'onda nell'arco di due decenni. Alla fine, hanno scoperto che il "ticchettio" degli "orologi" dei quasar si comportava proprio come previsto dalla relatività di Einstein: i quasar trovati in galassie lontane ticchettano più lentamente di quelli nati nell'universo successivo e vicino, con una dilatazione del tempo che fa sì che quelli più lontani evolvano ad un quinto della velocità di quelli più vicini. Ciò dimostra la necessità di perfezionare continuamente le nostre tecniche di analisi, anche quelle più consolidate, e d'altro canto la datazione accurata dei quasar antichi potrebbe rivelarsi utile per esplorare la natura dell'energia oscura, di cui parleremo più avanti.
Pensando alla colossale esplosione che ha "gonfiato" lo spazio e il tempo, e alla capacità della mente umana di penetrare a ritroso fino ad essa, non possono non venire in mente gli splendidi versi di Charles Baudelaire:
"Par dela le soleil, par dela les ethers,
par dela les confins des spheres etoilees,
mon esprit, tu te meus avec agilite,...
avec un indicible et male volupte"
[Al di là del Sole, al di là dell'etere,
al di là dei confini delle sfere stellate,
tu, mio spirito, ti muovi con scioltezza...
con indocile e maschia voluttà]
(C.Baudelaire, "Elevation")
.
7.7 Cosa sono i tensori?
Vogliamo ora descrivere quello che Einstein definì "il più grande errore della sua carriera" (!), non tanto per mostrare i suoi limiti, quanto piuttosto per mostrare come certi geni riescano ad aver ragione... persino quando sbagliano. Per comprendere il senso di tutto questo, è necessaria una parentesi matematica.
Abbiamo detto nel § 6.8 come la concezione einsteiniana sia completamente diversa da quella newtoniana; mentre infatti Newton riteneva che il moto dei gravi fosse dovuto alla reciproca attrazione tra le masse, Einstein continuò a ritenere che il moto seguisse le geodetiche dello spazio-tempo; ma la presenza di masse deforma ed incurva tale spazio, cambiandone completamente la geometria, e di conseguenza le geodetiche da rette diventano curve, talora molto complicate. È evidente che questo approccio, da un punto di vista matematico, è terribilmente più complicato del primo, dovendo trovare il legame tra la distribuzione di materia ed energia nel cosmo e la geometria dello spazio-tempo. Ma come si può descrivere una geometria completamente diversa da quella euclidea, a cui noi siamo abituati?
Allo scopo, bisogna introdurre grandezze di natura non scalare o vettoriale, bensì tensoriale. Come si sa, una grandezza si dice scalare se per descriverla basta un numero, mentre si dice vettoriale se per descriverla occorrono n componenti. In uno spazio tridimensionale basteranno tre componenti [ x1, x2 e x3 ], mentre nello spazio-tempo della Relatività Ristretta ne occorreranno quattro, dovendosi aggiungere anche il tempo. Ebbene, dicesi tensore n-dimensionale una grandezza rappresentata da una matrice n x n. Coinvolgendo le matrici, per trattare con i tensori sono necessari tutti gli strumenti dell'Algebra Lineare. Così, il prodotto di un vettore per un tensore si esegue con la regola del prodotto righe per colonne. Un tensore tridimensionale è allora caratterizzato da nove componenti, disposte su tre righe e tre colonne:

i indica il numero di righe, j indica il numero di colonne, ed entrambi in questo caso variano da 1 a 3.
Ad esempio, la temperatura assoluta è una grandezza scalare, bastando semplicemente un numero T per descriverla. Il vettore posizione di un corpo in un sistema di riferimento tridimensionale Oxyz sarà caratterizzato dalle sue tre componenti [ x y z ]. Un buon esempio di tensore è dato dal campo elettromagnetico T, che come si sa è la combinazione di campo elettrico E e campo magnetico B. Sia il vettore E che il vettore B sono dotati di tre componenti ciascuna: [ Ex Ey Ez ] e [Bx By Bz ]. In totale fanno sei componenti, dunque il campo elettromagnetico non può avere natura vettoriale. Ha invece natura tensoriale, come ci si accorge una volta che viene così riscritto:

Come si vede, è simmetrico rispetto alla diagonale principale, e quindi anziché nove componenti ne ha sei distinte tra loro.
Come possiamo servirci, ai nostri fini, di questo strumento matematico? Consideriamo due punti A ( x1; y1 ) e B ( x2; y2 ) di un comune spazio cartesiano bidimensionale. Per il teorema di Pitagora, la distanza tra i due punti è data dalla semplice formula:
![]()
Analogamente si opera in tre dimensioni:
Ora però, parlando del cronotopo (spazio-tempo) a proposito della Relatività Ristretta, abbiamo visto che è necessario introdurre le coordinate quadridimensionali di Hermann Minkowsky (1864-1909), nelle quali alle tre coordinate spaziali x, y, z bisogna aggiungere la coordinata temporale i c t, dove i è l'unità immaginaria. Tenendo conto che i2 = – 1, si ha così:
Queste distanze possono essere riscritte in forma tensoriale. Infatti la (7.3):
![]()
può venire così espressa:
dove x, y, z sono stati sostituiti con gli equivalenti x1, x2 e x3, e allo stesso modo la (7.4):
![]()
diventa allora:
c Δt può a sua volta essere sostituito con x0, per semplificare ulteriormente l'espressione. Einstein introdusse a questo punto una notazione che permette di riscrivere la (7.5) e la (7.6) nella forma:
ηαβ si dice tensore metrico, e descrive come è possibile misurare le distanze in una data geometria. Il caso più semplice è quello della (7.5), in cui:
ηαβ = diag [ + 1 + 1 + 1 ]
Questa si dice metrica pitagorica, e lo spazio è chiamato spazio cartesiano. L'insieme dei tre segni:
{ + + + }
prende il nome di segnatura dello spazio cartesiano: si tratta dei segni degli elementi della matrice diagonale ηαβ. Invece nella (7.6) si ha:
ηαβ = diag [ – 1 + 1 + 1 + 1 ]
e la sua segnatura corrisponde a:
{ – + + + }
Stavolta la metrica si chiama pseudopitagorica, e lo spazio pseudocartesiano o di Minkowsky. Si può dimostrare che le Trasformazioni di Lorentz, da noi descritte parlando della Relatività Ristretta, altro non sono che cambiamenti di coordinate, da pseudocartesiane a pseudocartesiane, nella geometria testé descritta.

Il
tunnel spaziale immaginato nella
serie "Star Trek, Deep Space Nine"
.
7.8 Le equazioni gravitazionali
Orbene, la presenza di masse deforma la geometria dello spazio-tempo in modo tale, da modificare completamente la metrica, e per descrivere il nuovo spazio-tempo non bastano più coordinate pseudocartesiane: bisogna passare alle cosiddette coordinate generali. Il tensore metrico in coordinate generali viene indicato con gαβ, per distinguerlo dalla metrica cartesiana ηαβ, e le coordinate generali verranno indicate con z1, z2, z3... per distinguerle dalle coordinate pseudocartesiane x1, x2, x3... Le coordinate generali più semplici sono le cosiddette coordinate sferiche, una generalizzazione delle coordinate polari, nelle quali ogni punto è rappresentato dalla distanza polare ρ dall'origine e dagli angoli θ e φ, detti rispettivamente ascensione retta e declinazione, che permettono di individuare una qualsiasi direzione nello spazio (ad es. le coordinate di una stella nel firmamento). Si può verificare che in esse la distanza al quadrato fra due punti è data da:
La precedente si può riscrivere:
![]()
una volta che si sia posto Δz1 = Δρ , Δz2 = Δθ , Δz3 = Δφ e:

Come si vede, la matrice gαβ sostituisce la matrice ηαβ della (7.7). ηαβ era costante in ogni punto, invece gαβ il tensore metrico in coordinate generali non lo è più, e dipende invece dalle coordinate spaziali (e temporali, includendo z0 = i c t ). Questo tensore contiene così tutte le informazioni sulla geometria dello spazio-tempo.
Ricapitolando: le coordinate cartesiane descrivono lo spazio euclideo della Fisica Classica di Galilei e Newton; le coordinate pseudocartesiane descrivono lo spazio pseudoeuclideo della Relatività Ristretta; le coordinate generali descrivono le varietà di Riemann (vedi § 6.7) governate dalle complesse geometrie non euclidee dello spazio curvato dalla gravità nella Relatività Generale. Quando all'equazione di una retta si applicano trasformazioni di coordinate da pseudocartesiane in generali, essa si trasforma nella complicata equazione di una geodetica, percorsa dalla luce in questo universo curvo. Quando si scrivono le equazioni del moto in coordinate generali lungo una geodetica, ci si accorge che compaiono nuovi complessi termini, detti termini di Christoffel, che risultano invece nulli quando il tensore metrico è costante, cioè nel cronotopo della Relatività Ristretta. Ebbene, Einstein ebbe la genialità di intuire che questi termini rappresentano le forze apparenti da noi introdotte nel § 6.1! In tal modo crolla la "dittatura" dei sistemi di riferimento inerziali, che la Relatività Ristretta aveva ereditato di peso dalla Fisica Classica: le forze apparenti, che costituiscono il fin qui insormontabile ostacolo alla scrittura di leggi valide per ogni osservatore, inerziale o non inerziale che sia, vengono spiegate allo stesso modo delle forze gravitazionali, cioè tramite un semplice passaggio da coordinate pseudocartesiane a coordinate generali! Affinché ciò non appaia come una semplice scappatoia matematica, si ricordi il famoso sistema delle "stelle fisse" di cui parlava Mach, come visto nel § 6.2: se ricordate, mentre le forze gravitazionali sono interpretabili come un cambiamento di curvatura dello spazio-tempo dovuto alle masse vicine, le forze apparenti sono interpretabili allo stesso modo, ma ricorrendo all'interazione con masse lontane. Se lo spazio è curvato dalla massa solare, la Terra si muove lungo la sua orbita ellittica; se è curvato dalla massa dell'intero universo circostante, compare il profilo parabolico dell'acqua nel secchio. Questo modello è sicuramente uno dei più geniali e convincenti che mente umana abbia mai concepito.
Si può dimostrare che, come ogni curva in un punto ha una retta tangente, e come ogni superficie in un punto ha un piano tangente, così ogni varietà di Riemann in ogni punto ha uno "spazio tangente", non rappresentabile visivamente, che ammette un sistema di coordinate pseudocartesiane: in esso dunque continuano a valere le equazioni della Relatività Ristretta e la curvatura dello spazio è nulla. Esso è noto come riferimento galileiano locale, ed in esso appare chiaro come la Relatività Ristretta sia un'approssimazione locale, riferita ad una regione assai ristretta dello spazio-tempo, della Relatività Generale, esattamente come in una regione molto ristretta il pianeta Terra, di forma sferica, si può ritenere dotato di superficie piatta!
Se gαβ (z) = ηαβ costante, le geodetiche spazio-temporali diventano rette, si torna al moto rettilineo uniforme e alle leggi della Relatività Ristretta. Basta però che gαβ (z) differisca di pochissimo da ηαβ , perchè il moto inerziale cambi completamente. Presa una massa M che genera un campo gravitazionale, e detta r la distanza da tale massa, a partire dalla (6.4) si può dimostrare che la nuova metrica circostante M è:
Se G M / r è piccola rispetto a c2, il termine diventa pari ad uno, e si torna alla metrica cartesiana, cioè tornano a valere le leggi del moto da noi descritte nel § 4.2 e seguenti. Ora, rispetto alle densità di massa incontrate sulla Terra e alla velocità della luce al quadrato, G è una costante piccolissima. È perciò necessaria una massa enorme per curvare apprezzabilmente lo spazio-tempo; la grandezza inversa 1/G si può considerare come una misura della "rigidità" dello spazio-tempo. In base alla nostra esperienza quotidiana, lo spazio-tempo è terribilmente rigido: basti pensare che l'intera massa della Terra produce una curvatura dello spazio-tempo pari appena ad un miliardesimo della curvatura della superficie terrestre!
Come si intuisce, la più grossa difficoltà dell'utilizzo dell'approccio di Einstein rispetto a quello di Newton consiste nel determinare il legame matematico tra la distribuzione di materia ed energia e la struttura della geometria dello spazio-tempo. Tale legame è fornito dalle equazioni gravitazionali di Einstein, probabilmente la più geniale creazione di quella mente geniale. Si tratta di equazioni estremamente difficili, giacché coinvolgono grandezze di natura tensoriale:
Le incognite sono i gαβ (z) , cioè i coefficienti del tensore metrico. Rαβ è il Tensore di Ricci, che deve il suo nome a Gregorio Ricci Curbastro, da noi già citato nel § 6.8, e misura la curvatura della varietà di Riemann in cui ci troviamo. R è la cosiddetta curvatura scalare, cioè la traccia del Tensore di Ricci, ottenuta sommando tutti i termini della sua diagonale principale. Tαβ è il cosiddetto Tensore energia-impulso, che descrive la densità e il flusso di energia e di quantità di moto associate al campo; c è la velocità della luce e G la costante di gravitazione universale (§ 2.2). La "geografia" dello spazio-tempo, cioè la distribuzione di materia e di energia descritta dal complicato tensore Tαβ , determina la "geometria" dello stesso, cioè la struttura della varietà di Riemann che descrive lo spazio curvato. Il tensore gαβ ha 4 x 4 = 16 componenti delle quali 10 indipendenti; tenendo conto che è indipendente per qualunque cambiamento di sistema di riferimento, come ci ha insegnato il Principio di Equivalenza (vedi § 6.3), e che ogni cambiamento contiene 4 costanti arbitrarie, le equazioni fra di loro indipendenti si riducono a sei. Le (7.10) sono perciò sei equazioni indipendenti tra loro.
Tali equazioni sono fortemente non lineari, mentre quelle legate alla gravitazione universale sono tutte equazioni lineari. Ciò rende estremamente difficoltosa la loro soluzione, tanto che le uniche soluzioni cui si è pervenuti senza l'uso di metodi numerici sono soluzioni approssimate, sotto certe ipotesi, o soluzioni rigorose di casi particolarissimi, dotati di determinate simmetrie. Il fatto che le equazioni (7.10) siano non lineari comporta il fatto che, se g'αβ e g"αβ sono due soluzioni distinte, una loro combinazione lineare del tipo (A g'αβ + B g"αβ ), con A e B costanti qualunque, NON è una soluzione accettabile. Fisicamente, ciò significa che il campo generato da due masse, supposte isolate nello spazio, non è pari alla sovrapposizione dei due campi generati singolarmente dalle due masse, ma bisogna aggiungere dei complessi termini di interazione. La cosa non deve però sorprenderci, se pensiamo a quanto ci ha insegnato la Relatività Ristretta a proposito dell'equivalenza tra massa ed energia. Il campo gravitazionale, come quello elettromagnetico, ha una sua energia (vedi § 4.1); ma, in base all'equazione E = m c2, l'energia si identifica con la massa, e quindi è sorgente essa stessa di campo gravitazionale. In altre parole, il campo è sorgente di campo! Si parla in questo caso di autosorgente. Essa è responsabile dei termini di interazione, e quindi della non linearità, dato che la massa genera un campo, e questo equivale a una massa aggiuntiva che genera nuovo campo, e così via. Proprio questa circostanza è responsabile dell'estrema difficoltà di una trattazione dell'energia gravitazionale, che infatti rimane un problema aperto.
Tra le soluzioni delle equazioni gravitazionali di Einstein nel caso di particolari simmetrie vi sono quelle riguardanti il mostruoso campo gravitazionale di un buco nero. Il già citato Karl Schwarzschild (vedi § 5.7) trovò infatti, poco prima di morire prematuramente nel 1916 durante la Prima Guerra Mondiale, una soluzione delle equazioni (7.10) chiamata metrica di Schwarzschild, che prevede un orizzonte degli eventi dal quale neppure la luce può più sfuggire. Oggi sappiamo che si tratta solo di un caso molto particolare, nel caso di un buco nero statico, il quale però dimostra che la relatività generale vale anche in ambienti con una gravità estrema. Per via del Principio di Conservazione del Momento Angolare, tuttavia, siccome la stella supergigante ruota su se stessa, deve farlo anche il buco nero in cui essa degenera; e per i buchi neri rotanti la metrica di Schwarzschild non basta più. Nel 1963 il matematico neozelandese Roy Patrick Kerr (1934-) trovò una soluzione detta in suo onore metrica di Kerr, secondo la quale i buchi neri sono definiti da due grandezze: massa e rotazione. Si tratta di una soluzione molto elegante, ma purtroppo fino al 2015 nessuno era riuscito a provarne sperimentalmente la correttezza: per verificarla, gli astrofisici dovrebbero registrare il moto di un oggetto mentre viaggia nella regione attorno a un buco nero per misurare la curvatura dello spazio-tempo. Alcuni buchi neri però misurano solo diversi chilometri di diametro, una distanza assai piccola su scala cosmica, e non è possibile tracciare singoli oggetti che si muovono in uno spazio così limitato a distanza di anni luce. Nel 2015 però Jonathan Gair e Christopher Moore dell'Institute of Astronomy dell'Università di Cambridge hanno usato un modello al computer per simulare diversi buchi neri con curve dello spazio-tempo che in qualche modo deviano dalla topografia descritta nella soluzione di Kerr: queste deviazioni sono chiamate "bumps", cioè "bernoccoli". Gli osservatori terrestri possono rilevare la strana curvatura attorno a questi buchi neri irregolari grazie ai raggi X emessi con caratteristiche che variano in funzione del loro campo gravitazionale. Gair e Moore hanno determinato quali deformazioni potrebbero essere rilevate in condizioni reali e quali, invece, si confonderebbero con un universo conforme alle leggi della relatività, identificando quattro protuberanze che diminuiscono entrambe nel modo più lento possibile e che potrebbero essere facilmente rilevate. Conoscere le "firme" caratteristiche nei raggi X che corrispondono a particolari "bernoccoli" del buco nero significa avere un punto di riferimento per i ricercatori che in futuro si occuperanno delle osservazioni in raggi X dei buchi neri. Forse l'osservatorio per raggi X ATHENA dell'Agenzia Spaziale Europea potrà effettuare queste osservazioni quando verrà lanciato, forse nel 2028.
Raffigurazione artistica di un "wormhole"
Ma non basta. Tra le soluzioni possibili delle equazioni (7.10) vi è il cosiddetto "wormhole" (letteralmente "cunicolo scavato da un verme"), introdotto per la prima volta nel 1957 da John Archibald Wheeler (1911-2008). In pratica, si tratta di una sorta di "cunicolo" quadridimensionale ottenuto congiungendo due aperture in uno spazio tridimensionale, analogamente al cunicolo tridimensionale con cui si possono collegare due fori praticati in una superficie bidimensionale (solo più difficile da visualizzare); vedremo nel § 8.8 l'importanza di questi wormhole nell'ambito della gravità quantistica. Dal momento che le due aperture possono trovarsi a una grandissima distanza nello spazio tridimensionale, ed il passaggio che le collega può renderle vicinissime, il wormhole è diventato un luogo comune nella fantascienza per spostarsi da un punto a un altro all'altro dell'universo a velocità maggiore della luce, in alternativa al motore a curvatura di Star Trek di cui abbiamo parlato nel § 6.11. Tale soluzione è stata adottata specialmente dal telefilm "Stargate SG1", in cui il wormhole è creato analogamente tra due stargate, dispositivi con la forma di anelli attraverso cui passano i protagonisti per ritrovarsi dall'altra parte della galassia; lo ritroviamo però anche nella serie "Star Trek, Deep Space Nine" sotto forma del tunnel spaziale bajoriano, in grado di congiungere due punti della Via Lattea distanti fra loro 70.000 anni luce. Proprio sui wormhole è poi basato il film di grande successo "Interstellar" (2014) del regista Christopher Nolan, a sua volta ispirato ad un lavoro del fisico americano Kip Thorne del California Institute of Technology: in un prossimo futuro la Terra è diventata inabitabile a causa dell'eccessivo0 sfruttamento delle sue risorse da parte dell'uomo, e l'unica speranza di salvezza per il genere umano consiste nel cercare altri pianeti abitabili attraverso un wormhole improvvisamente apparso presso Saturno, che si suppone aperto per noi da alieni benevoli; questi alieni si riveleranno poi essere i Terrestri del futuro, che hanno cercato di salvare dall'estinzione i loro antenati.
Già vi sento dire: sarebbe bello... sfortunatamente, però, anche se si potesse curvare lo spazio-tempo, il che è molto dubbio vista l'immensità delle energie in gioco, Wheeler dimostrò che, se la geometria dello spazio-tempo è regolata dalle equazioni di Einstein, il cunicolo è un oggetto dinamico, cioè le due aperture che esso collega sono necessariamente buchi neri. Ma allora, qualsiasi cosa entri in esse non ne può più uscire: il passaggio "si restringe" all'infinito, ed ogni cosa al suo interno, sia essa la Defiant del comandante Benjamin Sisko di Deep Space Nine, la squadra SG1 del Colonnello Jack O'Neill o l'"Endurance" del film "Interstellar", verrà compressa fino a una densità infinita prima di poter raggiungere l'altra uscita. A meno di eclatanti scoperte future, perciò, anche gli stargate e i tunnel spaziali continueranno a vivere solo nei serial di fantascienza...

Il cast della serie di fantascienza "Stargate SG1"
Nel 2023 gli astrofisici De-Chang Dai dell'Università di Yangzhou in Cina e Dejan Stojkovic dell'Università di Buffalo hanno suggerito un possibile metodo per cercare un wormhole all'interno di un buco nero, con osservazioni che sarebbero possibili entro un decennio. Se un wormhole esiste, secondo i due scienziati, si può presumere che qualunque stelle si trovi sul lato opposto eserciterebbe un'influenza gravitazionale, debole ma rilevabile, su quelle che stanno dalla nostra parte. E così, monitorando i movimenti delle stelle dalla nostra parte, potremmo cercare piccole accelerazioni percettibili causate dalla presenza di un wormhole. Se le osservazioni al telescopio del movimento di tali stelle raggiungessero una precisione di 0,000001 metri al secondo quadrato, tali misurazioni potrebbero rivelare l' impronta di una stella non molto più grande del Sole che attrae dal lato opposto del wormhole quelle visibili dalla nostra parte. Naturalmente, trovare una piccola accelerazione che corrisponde a una stella che si trova dall'altra parte non sarebbe la prova dell'esistenza del wormhole, ma potrebbe suggerire la presenza nelle vicinanze di invisibili buchi neri più piccoli. Se invece quell'accelerazione non fosse rilevata, e posto che ci si aspetta che esista un buco nero supermassiccio intorno a cui orbitano alcune stelle sull'altro lato di un wormhole, allora la presenza di quel passaggio nel buco nero supermassiccio potrebbe presumibilmente essere esclusa. Perché l'idea di Stojkovic e Dai funzioni, qualunque wormhole si trovi all'interno del buco nero deve essere privo di un orizzonte degli eventi, e quindi sarebbe diverso dall’idea del ponte di Einstein-Rosen di un buco nero da un lato e un buco bianco dall'altro. Come si vede, i punti di domanda sono tanti. Tuttavia, scoprire con certezza se c'è un wormhole al centro della nostra galassia potrebbe essere alla nostra portata entro dieci o quindici anni. Chi vivrà, vedrà.
A questo punto non possiamo non citare la ricerca condotta da Paolo Salucci della Scuola Internazionale Superiore di Studi Avanzati (Sissa) di Trieste, uno dei principali studiosi di materia oscura in Italia, insieme a Farook Rahman della Jadavpur University di Kolkata, in India: ricerca che potrebbe letteralmente aprire le porte a una nuova astrofisica. Secondo i calcoli di Salucci, infatti, le equazioni di Einstein (7.10) in base alle quali si genera un wormhole, può essere risolta usando come motore il campo gravitazionale della materia oscura presente nella galassia (vedi § 9.4). « Potrebbe essere solo una coincidenza », ha spiegato Salucci, « eppure è quanto meno sorprendente che l’equazione di Einstein relativa al wormhole possa essere risolta sostituendo alla discontinuità spazio-temporale, causata da un campo gravitazionale fortissimo come quello di un buco nero, i dati relativi al potenziale della materia oscura nella Via Lattea, che esercita, invece, un campo d’attrazione debolissimo ». Secondo la teoria di Salucci è quindi possibile che l’intera galassia possa essere intesa come un gigantesco sistema di trasporto interspaziale. Il passaggio potrebbe essere situato al centro della galassia e, secondo i calcoli teorici, sarebbe stabile e attraversabile. « Oggi la ricerca sulla possibile natura della materia oscura è in un vicolo cieco ». ha aggiunto il nostro scienziato: « quindi, in questo momento anche un’ipotesi fantascientifica regge meglio rispetto a quelle che sono considerate le teorie standard ».
Bisogna aggiungere che nel 2015 per la prima volta sono stati raccolti dati osservativi indicanti che la materia oscura potrebbe interagire con altra materia oscura in un modo diverso dall'attrazione gravitazionale. L'esistenza di questa interazione è testimoniata dalla identificazione di una massa di materia oscura situata a 5000 anni luce di distanza dalle galassie centrali dell'ammasso galattico Abell 3827. La scoperta è di un gruppo internazionale di astronomi guidati da Richard Massey (1977-) della Durham University, che stavano osservando i resti della collisione di ben quattro galassie all'interno di Abell 3827, ed è il frutto del confronto fra i dati spettroscopici ottenuti con lo strumento MUSE (Multi Unit Spectroscopic Explorer) del Very Large Telescope dell'ESO, in Cile, e le immagini riprese dal telescopio spaziale Hubble. La posizione della materia oscura è stata rilevata grazie al suo effetto di lente gravitazionale che distorceva l'immagine di una galassia molto più lontana di quell'ammasso. Questa lente gravitazionale non era però prodotta né dalle quattro galassie osservate né da alcuna altra galassia, e la sua fonte, invisibile, era leggermente spostata (in termini astronomici) rispetto a una delle quattro galassie centrali di Abell 3927. L'unica spiegazione del fenomeno è che, durante la collisione delle galassie, gli ammassi di materia oscura che le accompagnano abbiano interagito in qualche modo fra loro, creando una sorta di "attrito" che ha lasciato indietro la materia oscura di una di esse rispetto al movimento della sua galassia. Se la materia oscura venisse rallentata durante la collisione, potrebbe essere la prima prova di una diversa fisica dell'universo nascosto intorno a noi. I calcoli di Massey, pur non permettendo di stabilire la natura questa interazione, hanno escluso che sia di tipo gravitazionale. Questa informazione è preziosa perché, come osserva Liliya Williams, coautrice della ricerca, grazie a essa possiamo scartare alcune delle teorie fondamentali sulla composizione della materia oscura. Che sia venuto il momento di scoprire un nuovo universo? Solo le ricerche del futuro ci daranno la risposta.
.
7.9 I geni hanno ragione persino quando sbagliano...
Dopo aver pubblicato le proprie geniali equazioni gravitazionali (7.10), di cui egli andava giustamente fiero, Einstein tentò di costruire un modello di universo in accordo con la propria visione del mondo, peraltro condiviso da molti suoi colleghi: un universo statico, di densità uniforme e di raggio finito, che era sempre esistito e che sarebbe esistito per sempre. Nonostante i suoi tentativi, però, tale universo si rivelò instabile: come già osservato nel § 7.3, la gravitazione universale avrebbe fatto sì che tutte le masse si attirassero reciprocamente, facendo collassare l'universo in un unico punto.
Siccome però Einstein credeva fortemente nel principio di un universo eterno e statico, decise di modificare le proprie equazioni relativistiche aggiungendovi un nuovo termine, il famoso "termine cosmologico" indicato con la lettera greca Λ (lambda), il quale rappresenta una forza di repulsione tra le masse, in grado di agire solo tra masse enormi e su distanze grandissime. In tal modo, se la mela di Newton è attirata dalla Terra, due galassie molto lontane tenderebbero invece a respingersi tanto quanto la gravitazione la farebbe avvicinare, e così l'universo rimarrebbe statico. Le equazioni (7.10) andrebbero allora così corrette:
Λ avrebbe esattamente il valore necessario per mantenere statico l'universo; la sua introduzione "a posteriori" fu perciò criticata da molti come artificiosa, quasi Einstein volesse plasmare l'universo ad immagine del proprio cervello. Del resto, già nel 1917 il matematico olandese Willem de Sitter (1872–1934) individuò una soluzione delle equazioni gravitazionali (7.10) che prevedeva un universo in espansione, dodici anni prima della clamorosa scoperta di Hubble e Lemaître; per questo un universo in espansione è chiamato anche Universo di de Sitter. Naturalmente Hubble sgomberò il campo da ogni modello statico dell'universo, confermando che l'universo si espande, e quindi che ha avuto un inizio ed avrà una fine.
Albert Einstein dovette infine gettare la spugna e riconoscere che il cosmo in cui viviamo non è affatto statico, e così cancellò la costante cosmologica dalle equazioni (7.11), definendola « il più grande errore della mia carriera », avendogli impedito di arrivare alla formulazione dell'espansione universale prima che Lemaître ed Hubble se ne accorgessero con le loro misurazioni. Tuttavia, nessuna affermazione nella storia della scienza è da considerarsi una verità assoluta; ed infatti, anche "il più grande errore" della carriera di Einstein potrebbe rivelarsi come una straordinaria anticipazione.
Infatti, la gravitazione é la meno intensa tra le interazioni conosciute, eppure essa fa sentire in modo rilevante i suoi effetti proprio sull'evoluzione cosmologica: dato che tra le varie galassie si esercita un'attrazione reciproca, qualunque sia stata l'intensità iniziale dell'espansione, allora la logica vuole che questa proceda ad un ritmo meno intenso di quanto non avverrebbe se gli arcipelaghi stellari fossero del tutto indipendenti l'uno dall'altro. In altre parole, l'attrazione reciproca tra le galassie e gli ammassi di galassie dovrebbe frenare progressivamente l'espansione universale, facendola proseguire ad un ritmo sempre più lento. Così si credette per quasi settant'anni dopo la scoperta di Lemaître e di Hubble. Invece, l'8 gennaio 1998 Saul Perlmutter (1950–) del Berkeley Lab annunciò che le sue accurate misurazioni della velocità di allontanamento reciproco delle galassie dimostravano che l'espansione non sta affatto frenando; anzi, sta accelerando!
Come è possibile questo? Per spiegare questo incredibile comportamento è stato introdotto il concetto di "energia oscura", un'ipotetica forma di energia che si troverebbe in tutto lo spazio, come la famosa "etere" di Aristotele e poi dell'ottica ottocentesca, e con la sua pressione spingerebbe le galassie ad allontanarsi le une dalle altre. Secondo i calcoli di Perlmutter, l'universo sarebbe costituito per lo 0,5 % da oggetti stellari, per il 4 % da nebulose di gas intergalattico, per lo 0,3 % dagli sfuggenti neutrini e solo per lo 0,03 % da elementi pesanti, che costituiscono i pianeti come la Terra. Il 25 % sarebbe da imputare alla "materia oscura" (vedi § 9.4), e addirittura il 70 % da questa misteriosa "energia oscura" di cui nessuno oggi conosce la vera natura. La scoperta comunqwue fu così sensazionale che valse il Premio Nobel per la Fisica nel 2011 a Saul Perlmutter, Brian Schmidt e Adam Riess.

Un'ulteriore conferma dell'esistenza di una realtà fisica tanto esotica è venuta nel 2008 da un gruppo di astronomi dell'Università delle Hawaii guidati da István Szapudi, i quali hanno studiato le massime strutture conosciute nell'universo:, i superammassi di galassie, regioni di diametro fino a un miliardo di anni luce, in cui si addensano immense quantità di materia; e i supervuoti cosmici, regioni di volume comparabile a quello dei superammassi, ma praticamente prive di materia. Szapudi e collaboratori hanno studiato con cura certosina lo spostamento gravitazionale verso il rosso (vedi § 6.5), espresso dalla formula (6.3), subita dalla radiazione cosmica del fondo a microonde (§ 7.4) nel suo viaggio dal momento in cui fu emessa per la prima volta, circa 300.000 anni dopo il Big Bang, fino a giungere all'orecchio dei nostri radiotelescopi. In un universo piatto (vedi § 9.4) e dominato dall'energia oscura, questo effetto (detto anche Effetto Sachs-Wolfe) è rilevabile come un lievissimo riscaldamento (cioè aumento della frequenza) o raffreddamento (cioè diminuzione della frequenza, in base alla Legge di Wien (7.2)) dei fotoni della radiazione cosmica, a seconda che essi attraversino i superammassi, ad alta densità di materia, o i supervuoti, in cui la densità di materia è quasi zero. Szapudi e colleghi sono riusciti ad evidenziare questo effetto sotto forma di un segnale debolissimo, ma di fondamentale importanza, poiché ha rappresentato la prima prova diretta dell'esistenza dell'enigmatica energia oscura.
Un nuovo passo verso l'identikit dell'energia oscura è stato compiuto nel 2014 grazie alla Sloan Digital Sky Survey (SDSS), un ambizioso progetto internazionale di mappatura celeste, che ha permesso di misurare il tasso di espansione dell'universo con una precisione senza precedenti. Per riuscirci, sono state prese in considerazione alcune lontanissime galassie, analizzando come la loro luce viene assorbita dalle grandi nubi di idrogeno poste a varie distanze da noi. Per portare a termine un compito come questo, è necessario osservare un campione molto grande di galassie attraverso il Baryon Oscillation Spectroscopic Survey (BOSS), uno dei progetti portati avanti dal team della SDSS, le cui osservazioni sono iniziate nel 2000 e hanno condotto all'osservazione di 500 milioni di stelle e galassie. Il "cuore" della SDSS è un telescopio riflettore da 2,5 metri di diametro, installato a quasi 3000 metri di quota nell'Osservatorio di Apache Point in Arizona.
Le nubi di idrogeno intergalattiche disperse nello spazio fra noi e le più remote galassie assorbono diversi colori della luce emessa da quelle più lontani. Gli astronomi impegnati nel BOSS hanno quindi potuto misurare di quanto l'universo si sia espanso fra le epoche in cui la luce ha attraversato le varie nubi di idrogeno. Si tratta di un metodo pionieristico, che sfrutta la distribuzione delle nubi di gas su grandissima scala, e che ha permesso di concludere che circa 11 miliardi di anni fa l'Universo si espandeva di circa l'1 % ogni 44 milioni di anni. « Poco più di un anno fa abbiamo tentato per la prima volta e mostrato che questo sistema funziona davvero », ha commentato Matthew Pieri dell'Istituto di Cosmologia e Gravitazione dell'Università di Portsmouth. « Ora ci siamo ritornati con il doppio dei dati e con una notevole precisione del 2 %. Stiamo misurando l'espansione dell'Universo in grandissimo dettaglio. Come gli anelli nel tronco di un albero ci dicono la sua età, lo spettro di ogni galassia diventa un archivio della storia dell'universo ». La strada è ovviamente ancora lunga, e la grandissima precisione delle misure potrebbe svelare delle sorprese sulla nostra visione del cosmo. Ma questa energia oscura da quale meccanismo fisico può saltare fuori?

Le equazioni gravitazionali di Einstein
dipinte da un anonimo
autore su
una locomotiva abbandonata a Uyuni, nella regione di Potosì, in Bolivia
.
Quando Richard Feynman (1918–1988) sviluppò la teoria quantistica della radiazione, si rese conto che anche il vuoto possiede una sua ben definita energia, provocata dalle particelle virtuali che si formano in continuazione. Il principio di indeterminazione di Heisenberg infatti afferma tra l'altro che l'energia e la durata di un fenomeno non possono essere entrambi zero. Di conseguenza il vuoto assoluto non può esistere, poiché in esso energia e durata dei fenomeni sono appunto nulli. Nel vuoto si generano in continuazione coppie di particelle e antiparticelle, per poi annichilarsi a vicenda: quello che noi crediamo il "vuoto" è in realtà un pauroso ribollire di particelle (virtuali, perché non rilevabili) che interagirebbero globalmente con la materia ordinaria, dando vita all'accelerazione dell'universo. Questa situazione è chiamata "vuoto quantistico", e ne riparleremo nel § 8.5. Insomma, l'energia oscura sarebbe una sorta di energia intrinseca dello spazio ("il prezzo della pace per avere spazio", come lo ha definito un fisico). Da qui nasce l'esigenza di rispolverare proprio la costante cosmologica Λ già scartata da Einstein, riportando le equazioni di Einstein alla forma (7.11): alla faccia del più grande errore di Einstein!
Il valore migliore stimato da Saul Perlmutter per la costante cosmologica è dell'ordine di circa 10−29 g/cm3. Il problema è che la maggior parte delle teorie quantistiche dei campi prevedono un valore enorme per la costante dall'energia del vuoto quantistico, fino a 120 ordini di grandezza in più: è questo il massimo sfasamento tra teoria e misure in tutta la storia della Fisica! Altri fisici allora hanno pensato all'energia oscura come ad una "quintessenza" (appunto, come l'etere aristotelica: torna l'eterna ossessione dei cosmologi!) chiamata anche "energia fantasma". Alcuni puntano su teorie alternative, innovative ed estremamente complesse, come la teoria delle Superstringhe o la Gravità Quantistica a Loop, le quali potrebbero spiegare la costante cosmologica senza far ricorso all'energia oscura.
Bisogna aggiungere che l'enigmatica energia oscura sta sfuggendo a qualunque tipo di rilevazione strumentale, mentre dal punto di vista teorico ci si sta interrogando sulla sua natura, incontrando problemi che al momento paiono insormontabili. C'è anche chi pensa che l'energia oscura e l'accelerazione cosmica siano la prova del fallimento del modello Standard fin qui accettato, poiché costringe ad ammettere l'esistenza di qualcosa non ancora interpretabile come l'energia oscura. Tutte queste difficoltà hanno spinto alcuni cosmologi a studiare nuovi modelli di universo che possano fare a meno dell'energia oscura. In particolare secondo un gruppo di ricercatori guidato da Gábor Rácz, della Eötvös Loránd University di Budapest, in Ungheria, si può evitare l'introduzione dell'energia oscura nei modelli di universo, a patto di considerare l'evoluzione nel tempo della sua struttura a grande scala, ovvero il fatto che galassie e ammassi di galassie non si distribuiscono uniformemente nello spazio, ma tendono ad aggregarsi in filamenti, lasciando nel contempo enormi spazi vuoti. Abbandonando quindi l'ipotesi di omogeneità dell'universo, condizione iniziale applicata fino a oggi per calcolare soluzioni semplificate delle equazioni gravitazionali di Einstein, altrimenti troppo complesse, e viceversa considerando l'esistenza delle strutture cosmiche, Rácz e collaboratori hanno sviluppato alcune simulazioni numeriche che evidenziano come varie regioni dl universo evolvono e si espandono con velocità differenti, dando luogo a un'espansione differenziale. I risultati delle simulazioni restano in accordo con le osservazioni (il tasso medio di espansione è pari a quello osservato e l'espansione complessiva è accelerata), tuttavia non serve più l'ipotesi dell'energia oscura. II gruppo di Rácz è al lavoro per perfezionare ulteriormente le simulazioni, ma la discussione tra cosmologi e già avviata. In ogni caso, distinguere quale sia il modello migliore tra l'energia del vuoto, la quintessenza e gli altri richiede misure accuratissime dell'espansione dell'universo per capire come la sua velocità cambia nel tempo, e capire quanto poco è stato sbagliato "il più grande errore" di Einstein sarà uno degli sforzi maggiori della Fisica e della Cosmologia nel corso del XXI secolo.

Fino a qui, però, abbiamo parlato solo degli effetti relativistici della forza di gravità; possibile che su di essa non agiscano anche degli effetti quantistici? Lo scoprirete se salterete con me al capitolo seguente, che sarà uno dei più densi di teorie innovative dell'intero ipertesto! Per tornare all'indice, invece, il link è questo.
![]()