![]()
|
"Quand'io
mi volsi, tu passasti 'l punto Dante, Inferno XXXIII, 110-111 |
.
2.1 La centralità della forza di gravità
Si sa che il grande contributo di Isaac Newton (1642-1727) alla Fisica è costituito dalla sistematizzazione delle leggi del moto scoperto da Galileo e dalla formulazione della Seconda Legge della Dinamica (forza uguale massa per accelerazione) nei suoi fondamentali "Philosophiae Naturalis Principia Mathematica" (1687). Ma non meno importante è stata l'ideazione di quella teoria che va sotto il nome di Gravitazione Universale, e che condusse alla scoperta delle quattro forze della natura.
Il nocciolo di questa teoria sta nell'ipotesi che sia i moti terrestri, sia i moti celesti siano interpretabili per mezzo di una sola interazione, che agisce tra le masse dei diversi corpi. In altre parole, una mela staccatasi dall'albero cade verso la Terra attratta dalla stessa forza che mantiene la Luna in un'orbita circolare attorno ad essa: la differenza tra i due moti sta solo nelle diverse masse e nelle condizioni iniziali del moto.
È abbastanza naturale che questa interazione reciproca tra due masse dipenda da entrambi i loro valori, cioè dalla "quantità di materia" contenuta nei loro corpi. Più difficile è determinare la sua dipendenza dalla distanza tra le due masse (o meglio, tra i loro centri di massa). A questo scopo ci vengono in aiuto le Tre Leggi di Kepler, che val la pena di riprendere in mano per analizzarle nei dettagli.
La Seconda Legge, detta anche Legge delle Aree, ci assicura che il moto planetario non avviene a velocità uniforme. Per la precisione, i pianeti si muovono più rapidamente quanto più si trovano vicini al Sole. Il perchè è comprensibile osservando la figura sottostante: se i due triangoli FAB ed FCD sono "spazzati" nello stesso tempo Δt dal raggio vettore, è evidente che deve essere CD > AB, in quanto essi hanno altezze ben diverse. Ed essendo uguali i tempi impiegati per percorrerli, la velocità deve essere maggiore vicino al fuoco. Per questo si dice che il pianeta è più veloce al perielio che all'afelio.
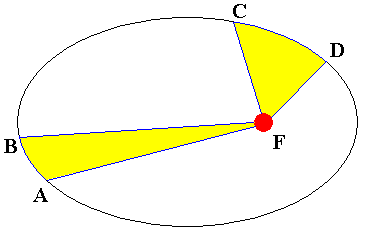
La Legge delle Aree insomma ci dice che:

Introduciamo ora il concetto di velocità areolare, definita come il rapporto tra l'area percorsa e il tempo impiegato a "spazzarla". La Legge delle Aree si può allora così esprimere:
La velocità areolare di un pianeta nel suo moto attorno al Sole è costante.
Facendo tendere Δt a zero, si può introdurre anche il concetto di velocità areolare istantanea:

Ora dimostreremo che il fatto che vA è costante implica che anche il momento angolare è costante nel moto planetario. Il fatto che in qualche modo nelle leggi di Kepler è implicato il momento angolare L del pianeta è confermato dalla Prima Legge. Se infatti l'orbita è ellittica, allora è piana. Allora le velocità v e v' del pianeta nei due punti P e P' della loro orbita giacciono nello stesso piano dei raggi vettori r ed r'. Per definizione si ha allora:

Ma la massa è scalare, dunque non ha effetto sulla direzione. Siccome il prodotto vettoriale di due vettori è ortogonale al piano da essi individuato, ne segue che sicuramente L è parallelo a L'. Dunque la Prima Legge di Kepler mi garantisce che il momento angolare conserva direzione costante!
Ora, tutti i pianeti del Sistema Solare ruotano più o meno nello stesso piano, chiamato eclittica. Posto che la Terra ruoti esattamente in essa, quello che se ne discosta maggiormente è Mercurio, con soli 7° di inclinazione. Invece i pianeti nani più esterni se ne discostano assai di più: Plutone di 17° 12', Haumea di 28° 12', Eris addirittura di 44° 11'. I pianeti hanno perciò tutti momenti angolari tra loro paralleli. Supponiamo dunque, come si vede nel disegno sottostante, che il pianeta descriva una traiettoria tale da portarlo da P a P' in un tempo Δt piccolo a piacere. L'area ΔA spazzata dal raggio vettore in questo intervallo di tempo è quella del triangolo mistilineo OPP', qui evidenziata in azzurro:

Siccome il tempo Δt è piccolo, l'arco PP' si può ritenere pressoché rettilineo, e dunque per una semplice legge della geometria euclidea avremo:
Scomponendo la velocità tangenziale v nei suoi due componenti radiale e trasversale, ci rendiamo conto che quest'ultimo è diretto proprio come PH, che è perpendicolare al raggio vettore. Ne consegue che:
![]()
Sostituendo nella (2.2) ho:

che si può riscrivere:

ma l'angolo α è quello che i vettori r e v formano tra le loro direzioni, per cui r v sen α è il modulo del loro prodotto vettoriale! Possiamo perciò scrivere:

Moltiplicando e dividendo per la massa m del pianeta, e ricordando le (2.1), si ha:

In altre parole, la velocità areolare del pianeta è direttamente proporzionale al suo momento angolare. Ma la Seconda Legge di Kepler ci dice che la velocità areolare del pianeta è costante; ne consegue che il momento angolare del pianeta è costante anche in modulo!
Quali le conseguenze di tutto questo? La Seconda Equazione Cardinale della Dinamica ci dice che:

Se L è costante, la sua variazione è nulla, quindi il primo membro è nullo. Allora è nullo anche il prodotto vettoriale tra il raggio vettore e la forza che il Sole esercita sul pianeta. Quando un prodotto vettoriale di due vettori non nulli è nullo? Quando essi sono paralleli tra loro! Ne consegue che la forza F è diretta come il raggio vettore, e quindi che la forza esercitata dal Sole sul pianeta è diretta lungo la congiungente tra i due corpi. In altre parole, la forza di gravità è centrale.
.
2.2 Una legge universale
Le prime due Leggi di Kepler ci hanno assicurato che la forza di gravità è diretta lungo la congiungente i centri di massa dei due corpi; ora bisogna decidere come varia la forza in funzione della distanza r. Allo scopo, facciamo ricorso alla Terza Legge. Perchè il pianeta ruota? Perchè esso è soggetto a una forza centripeta che lo costringe a cambiare direzione in ogni istante, restando vincolato alla sua orbita:

Appare abbastanza chiaro che tale forza centripeta FC coincide con la forza di gravità FG che il Sole esercita sul pianeta. La Prima Legge di Kepler ci dice che le orbite dei pianeti sono ellittiche; tuttavia, siccome la loro eccentricità è piuttosto piccola (va dallo 0,007 di Venere allo 0,093 di Marte, l'unico a discostarsene molto è Mercurio con 0,206), semplificheremo i calcoli ipotizzando un moto circolare uniforme. Avremo allora:
Ora, noi sappiamo che nel moto circolare uniforme la velocità tangenziale è data da:

Sostituendo questa formula nella (2.3) otteniamo:

Utilizziamo ora la (1.1), cioè la Terza Legge di Kepler:

Ma, come si è detto, FG deve dipendere anche dalla massa M del Sole. Moltiplico e divido numeratore e denominatore della precedente, ed ho:
Ne segue che la forza che mantiene il pianeta sulla sua traiettoria è inversamente proporzionale al quadrato della distanza. Ponendo:
la (2.4) assume la forma seguente:
Quella ora scritta è la celeberrima LEGGE DI GRAVITAZIONE UNIVERSALE:
La forza di gravità che si esercita tra due corpi è direttamente proporzionale alle masse dei due corpi, inversamente proporzionale al quadrato della loro distanza ed è diretta lungo la congiungente i loro centri di massa.
La costante G si chiama costante gravitazionale. Come si vede dalla (2.5), essa contiene la massa del Sole e la costante di Kepler k, che caratterizza il Sistema Solare. Ma a questo punto Newton ebbe un colpo di genio, che secondo la leggenda gli fu ispirata dalla proverbiale mela che dà il titolo a questo ipertesto: intuì che la (2.6) vale per tutti i corpi dell'universo, e non solo tra il Sole e uno dei suoi pianeti. Tra tutte le masse insomma si esercita una forza che ha le caratteristiche descritte dalla (2.6). Più i corpi sono massicci, e più l'interazione è intensa. Più sono lontani, più essa è debole. Ed allora anche il moto dei gravi verso il basso è spiegato da questa legge, senza più ipotizzare un "moto naturale" dall'alto verso il basso, come descritto nel paragrafo 1.3: se questa forza si esercita anche tra la Terra e la mela che sarebbe cascata in testa a Newton, evidentemente la mela acquista un'accelerazione e si muove verso la Terra. A quest'ultima si applica una forza uguale e contraria, ma la Terra è troppo massiccia per muoversi a sua volta, e così l'unica a muoversi in effetti è la mela. Anche il moto planetario viene perfettamente descritto, senza più far ricorso al presunto moto naturale circolare uniforme dell'etere. Viene definitivamente a cadere ogni barriera tra il nostro mondo e il mondo degli astri, entrambi regolati dalle stesse leggi del moto. La (2.6) assume perciò il carattere di LEGGE UNIVERSALE, valida cioè tra tutti i corpi dell'universo!
Quest'affermazione, però, va certamente provata. Come verificare che la (2.6) sia valida anche per masse non planetarie? La prova definitiva fu trovata da Henry Cavendish (1731-1810), che nel 1798 ideò la cosiddetta bilancia di torsione, illustrata qui sotto. Essa è costituita da due masse fisse m', di notevole entità, e da un "equipaggio" sospeso, formato da un'asta che reca alle estremità due masse m. Avvicinando le masse m' alle m, queste ultime vengono attratte e l'equipaggio è sottoposto ad una coppia di forze, che lo fa ruotare. Conoscendo l'elasticità del filo, e misurando l'angolo di rotazione, è possibile risalire all'entità della coppia che fa ruotare l'equipaggio, e quindi alle forze in gioco. Ma l'angolo di rotazione è piccolissimo: come misurarlo con la debita precisione? Cavendish ebbe l'idea di collegare al filo uno specchietto, di far riflettere su di esso il raggio di luce di una lampada, e di far incidere il raggio riflesso su una scala graduata molto lontana, in modo da amplificare gli effetti della rotazione. Il tutto è racchiuso dentro un contenitore isolato, in modo da evitare che eventuali correnti d'aria disturbino l'esperimento.


Raddoppiando le masse m', si osserva che l'angolo di torsione raddoppia, segno che l'intensità della forza gravitazionale è raddoppiata. Idem accade raddoppiando le masse m'. Raddoppiando la distanza, invece, la forza si riduce ad un quarto. In tal modo, è possibile verificare la validità della (2.6) per qualsiasi massa.
Affinando le misure, è possibile anche valutare l'entità della costante G che, come vedremo nel § 8.7, è una delle tre costanti fondamentali della Fisica moderna. Ma non è questo l'unico modo per determinare il valore e l'universalità di G. Nel 2014, nell'ambito dell'esperimento denominato MAGIA, Guglielmo Tino e colleghi dell'Università di Firenze e dell'Istituto Nazionale di Fisica Nucleare (INFN) hanno misurato con un metodo del tutto nuovo e con alta precisione la costante gravitazionale, fino ad allora affetto da una notevole incertezza, perché le misurazioni effettuate in diversi laboratori davano valori spesso tra loro non consistenti. « Le misurazioni condotte finora erano tutte basate su forme più o meno avanzate della bilancia di torsione di Cavendish, nel senso che misuravano l'effetto gravitazionale di una massa macroscopica su una massa molto più piccola », ha spiegato il professor Tino. Il metodo utilizzato da quest'ultimo e dai suoi colleghi era invece innovativo, basando si sulla tecnica dell'interferometria atomica. « Un interferometro atomico è l'analogo di un interferometro ottico, uno strumento molto utilizzato nella fisica sperimentale, in cui un fascio di luce è separato in due sottofasci, che sono indirizzati lungo cammini ottici separati e poi ricomposti in un punto in cui si osserva il fenomeno dell'interferenza », ha aggiunto Tino. « Nel nostro apparato ciò che viene separata è l'onda di materia, ovvero l'onda che in meccanica quantistica è associata a una particella, e quindi anche ad un atomo; noi non facciamo altro che separare in due l'onda materia di un atomo per poi osservarne la figura d'interferenza, che dipende dalla costante di gravitazione ». MAGIA del resto sta proprio per « Misura Accurata di G mediante Interferometria Atomica ». Nell'apparato sperimentale di MAGIA, atomi di rubidio mantenuti alla temperatura di pochi milionesimi di grado sopra lo zero assoluto venivano lanciati verso l'alto nel vuoto, grazie a un fascio laser, in una specie di " fontana atomica", e quindi risentivano dell'attrazione gravitazionale della Terra. Quest'ultima veniva tuttavia modificata per una quantità piccolissima, di una parte su 10 milioni, grazie ad opportune masse di tungsteno. « Il nostro interferometro è così sensibile che si riesce a rilevare l'effetto delle masse sorgenti e a determinare G con elevata precisione, pari allo 0,015 per cento », ha concluso il prof. Tino. Il valore di G oggi comunemente accettato dal Committee on Data for Science and Technology (CODATA) è:
![]()
Come si vede, è un valore piccolissimo! Esso comporta che due masse di 1 Kg alla distanza di 1 metro si attraggono con una forza di appena 0,067 miliardesimi di Newton! Ciò spiega perchè noi non restiamo incollati l'uno all'altro per via della forza di gravità: una forza del genere non può assolutamente vincere la nostra inerzia, e noi non ci accorgiamo neppure che tale interazione reciproca esista. Ce ne accorgiamo però se le masse in gioco diventano enormi, per esempio se una di esse è quella della Terra. Ed ecco perchè noi veniamo attratti verso il centro della Terra dalla forza peso, una forza ben nota anche a Dante Alighieri, che fa dire a Virgilio:
«
...quand'io mi volsi, tu passasti 'l punto
al qual si traggon d'ogne parte i pesi. » (Inf. XXXIII, 110-111)
.
2.3 L'inverso del quadrato
Proprio utilizzando la gravità terrestre, Newton verificò immediatamente la validità della legge dell'inverso del quadrato. Infatti, se la (2.6) vale tra le forze, deve necessariamente valere anche tra le accelerazioni. Proviamo allora a confrontare l'accelerazione centripeta della Luna attorno alla Terra con l'accelerazione di gravità del nostro pianeta. La Luna dista in media dalla Terra 384.000 Km, cioè 3,84 x 108 m, ed impiega 27 giorni, 7 ore e 43 minuti per completare una rivoluzione, cioè 2,36 x 106 secondi. Si ha perciò:

Si ha perciò:

Ma la distanza Terra-Luna r equivale pressappoco proprio a 60 raggi terrestri R, per cui si può affermare con buona approssimazione che:

e quindi, nei limiti di esattezza del nostro calcolo approssimato, le due accelerazioni sono inversamente proporzionali ai rispettivi quadrati delle distanze.
Vi è un altro ragionamento che prova immediatamente la validità della legge dell'inverso del quadrato. Si osservi la foto sottostante: una sorgente luminosa puntiforme emette dei raggi di luce in ogni direzione. Un'area posta a distanza r dalla sorgente la illumina con un'intensità I. Se raddoppio la distanza, scopro che la stessa intensità luminosa si distribuisce su un'area quattro volte più estesa (in solidi simili le aree sono direttamente proporzionali ai quadrati delle distanze), e dunque un'area A equivalente a quella a distanza r dalla sorgente riceve un'illuminazione pari a un quarto di I. Se la distanza la triplico, scopro che la stessa intensità luminosa si distribuisce su un'area nove volte più estesa, e dunque ogni area pari ad A riceve solo un'intensità I/9. Questo spiega perchè, raddoppiando, triplicando, ecc. la distanza, l'intensità della forza gravitazionale diventa un quarto, un nono, eccetera!

Il lettore più attento si sarà accorto che la dimostrazione fin qui eseguita vale solo per masse puntiformi e per traiettorie circolari percorse di moto uniforme. Tuttavia, con calcoli più complessi è possibile dimostrare che la legge di Newton vale in generale anche per orbite ellittiche e per masse estese; in quest'ultimo caso, le masse si potranno ritenere concentrate nel loro baricentro. La dimostrazione di quest'ultima affermazione richiese a Newton l'elaborazione del calcolo integrale, da lui messo a punto proprio per questo scopo, e spiega perchè egli elaborò la teoria della gravitazione universale nel 1666, ma la pubblicò solo nel 1687, dopo aver messo a punto un'intera branca della matematica, il calcolo differenziale ed integrale! Chi è interessato alla dimostrazione rigorosa con tutti i passaggi matematici, la troverà nell'Appendice.
.
2.4 Determinazione della massa della Terra
Vediamo ora alcune applicazioni pratiche della (2.6). Si voglia anzitutto determinare la massa MT della Terra. Noi sappiamo che il peso di un corpo è dovuto all'attrazione da parte della gravità terrestre:
FG = P
Ma il peso P è pari alla massa m del corpo per la sua accelerazione di gravità g, e quindi:

dove RT è il raggio terrestre (la Terra è supposta perfettamente sferica). La massa m del corpo si semplifica e si ha così:
Come si vede, la forza di gravità è indipendente dalla massa del corpo, cosa del resto già ben nota sperimentalmente: tutti i corpi sulla terra cadono con la stessa accelerazione di gravità, fatta salva la resistenza dell'aria; ed infatti una moneta e una piuma giungono a terra nello stesso istante, se lasciati cadere dentro un tubo in cui è stato praticato il vuoto. Dalla (2.7) segue allora:

Dunque la Terra ha una massa pari a quella di circa 2000 miliardi di miliardi di elefanti! Conoscendo il raggio terrestre, è possibile ricavare il volume del nostro pianeta. e quindi la sua densità, che risulta pari a circa 5,52 Kg m-3: una densità assai maggiore di quella della crosta terrestre, la quale fa pensare che il mondo abbia un grosso nucleo di ferro. La moderna geologia ha poi confermato questo asserto; per maggiori informazioni al riguardo, consultate il mio ipertesto intitolato "L'Anno della Terra".

Isaac Newton interpretato dall'attore Peter Dennis nella puntata di "Star Trek, Voyager" intitolata "Death Wish" (da questo sito). In tale puntata si viene a sapere che è stato l'alieno Quinn ad urtare un melo, facendo cadere il frutto che ispirò allo scienziato inglese la teoria della Gravitazione Universale!
.
2.5 Determinazione della massa del Sole
Determiniamo ora la massa MS del Sole. Se un pianeta resta sulla sua orbita, abbiamo detto che ciò avviene per effetto di una forza centripeta che coincide con l'attrazione gravitazionale solare. Allora:
FG = FC
cioè:

MT si elide, e si ricava:

Osserviamo che:

Il Sole contiene dunque 330.000 masse pari a quelle della Terra, e siccome ha un diametro 101 volte maggiore, ha un volume un milione di volte maggiore, per cui la densità del Sole è solo un terzo di quella terrestre, e precisamente pari a circa 2,7 Kg m-3.
Da notare che la fortissima attrazione gravitazionale del Sole è responsabile di due fenomeni cui conviene fare cenno. Il primo è quello delle maree. Con questo termine si indica il moto periodico di grandi masse d'acqua (oceani, mari, i laghi più vasti) che ne provoca il regolare innalzamento (alta marea) e abbassamento (bassa marea) di livello con frequenza di circa sei ore. Il dislivello può arrivare nell'oceano fino ai 16 metri registrati nella Baia di Fundy, sulla costa atlantica del Canada. Secondo Galileo Galilei, il flusso e riflusso delle maree era da imputarsi unicamente alla forza centrifuga dovuta alla rotazione della Terra intorno al Sole, come affermato nel "Dialogo sui Massimi Sistemi":
« Mi son quasi sentito non leggiermente tirare ad ammettere (fatti però i presupposti necessari) che quando il globo terrestre sia immobile, non si possa naturalmente fare il flusso o reflusso del mare; e che quando al medesimo globo si conferiscono i movimenti già assegnatili, è necessario che il mare soggiaccia al flusso e reflusso, conforme a tutto quello che in esso viene osservato. » (Giornata Quarta)
Egli perciò riteneva le maree una delle prove principali a favore del Modello Eliocentrico (§ 1.4). Già lo scienziato greco Posidonio di Apamea (135–50 a.C.), il suo collega medioevale Jacopo Dondi dell'Orologio (1293–1359) e l'astronomo rinascimentale Federico Crisogono (1472–1538) avevano attribuito il fenomeno delle maree all'attrazione gravitazionale congiunta esercitata sulla Terra dalla Luna e dal Sole, come divenne finalmente chiaro dopo la formulazione della Gravitazione Universale di Newton. Oggi inoltre sappiamo che l'attrito tra gli oceani e i litorali causato dalle maree porta ad un continuo rallentamento della rotazione terrestre, la cui durata cala di circa venti microsecondi per anno.
Il secondo importante fenomeno dovuto all'attrazione solare è la cosiddetta Precessione degli Equinozi, scoperta nel 135 a.C dall'astronomo greco Ipparco di Nicea (190–120 a.C.): l'asse di rotazione terrestre, inclinato di 23° 27', non rimane costantemente parallelo a se stesso, ma descrive lentamente un doppio cono con un periodo di circa 25.770 anni ("Anno Platonico"). La causa di questo moto lentissimo è da ricercarsi proprio nell'attrazione gravitazionale esercitata dal Sole e dalla Luna sul rigonfiamento dell'equatore terrestre, dal momento che la Terra è una sfera schiacciata ai poli. Si parla di Precessione degli Equinozi perché, in conseguenza di questo moto, la linea immaginaria che congiunge i punti equinoziali non rimane ferma, ma ruota a sua volta intorno al centro della Terra: gli equinozi si spostano quindi lungo l'orbita di circa 50 secondi d'arco ogni anno. Sempre in conseguenza del moto di precessione, il Polo Nord Celeste non rimane fisso, ma descrive sulla volta celeste una circonferenza con lo stesso periodo di circa 26.000 anni. La Stella Polare non è sempre stata e non sarà per sempre α Ursae Minoris, la stella poco brillante che oggi è la più vicina al Polo Nord Celeste. Dal 3942 al 1793 a.C., mentre sulla Terra nascevano le prime civiltà monumentali, l'asse terrestre puntava verso α Draconis, nota anche con il nome di Thuban (in arabo "drago"), nella costellazione del Dragone: un astro ancora più debole della odierna Polare, cinque volte meno luminosa di essa. Invece verso il 12.000 a.C. il ruolo di stella polare era invece ricoperto dalla brillantissima stella Vega (α Lyrae), la quinta stella più luminosa dei cieli dopo Sirio, Canopo, Arturo ed α Centauri; questo magnifico astro, dal quale nella saga di "Goldrake" provenivano i malvagi alieni intenzionati a distruggere ed assoggettare la Terra, tornerà ad essere la Polare intorno all'anno 13.800 d.C.


La precessione degli equinozi e il moto nel firmamento del Polo Nord Celeste
.
2.6 Determinazione dell'accelerazione di gravità sul Sole
A questo scopo utilizziamo la (2.7), con la massa del Sole testé calcolata e il raggio solare RS = 696.000 Km al posto di quelli terrestri. Segue subito che:

Di questo risultato ci serviremo nel § 6.4. Ora, poiché:

ne consegue che la massa di 1 Kg sulla Terra ne peserebbe ben 28 sul Sole! Tralasciando la temperatura superficiale di oltre 6000° C, sulla superficie solare la vita umana sarebbe impossibile: non solo alzare un piede sarebbe un'impresa da Titani, ma il cuore non ce la farebbe neppure a pompare il sangue fino al cervello!
Ecco una tabella con le accelerazioni di gravità sui principali corpi del Sistema Solare, misurate in metri al secondo quadrato (seconda colonna) e in rapporto all'accelerazione di gravità terrestre gT (terza colonna):
|
Corpo |
g |
g/gT |
tipo |
|
Mercurio |
3,701 |
0,377 |
pianeta |
|
Venere |
8,870 |
0,904 |
pianeta |
|
Terra |
9,803 |
1 |
pianeta |
| Luna | 1,622 |
0,165 |
satellite |
|
Marte |
3,690 |
0,376 |
pianeta |
|
Cerere |
0,278 |
0,028 |
pianeta nano |
|
Giove |
23,12 |
2,358 |
pianeta |
| Ganimede | 1,430 |
0,146 |
satellite |
|
Saturno |
8,960 |
0,914 |
pianeta |
| Titano | 1,350 |
0,138 |
satellite |
|
Urano |
8,691 |
0,886 |
pianeta |
|
Nettuno |
11,15 |
1,140 |
pianeta |
| Tritone | 0,780 |
0,079 |
satellite |
|
Plutone |
0,533 |
0,054 |
pianeta nano |
.
Come si vede, con queste semplici formule è possibile calcolare le masse e le accelerazioni di gravità di tutti i corpi celesti, purché dotati di satelliti. In questo modo ad esempio non è possibile calcolare la massa della Luna, giacché essa è priva di satelliti naturali, e la sua massa si elide sempre nei calcoli fin qui svolti. Tuttavia, è possibile calcolare per altra via pure le masse dei satelliti: infatti il moto dei corpi celesti sarebbe perfettamente ellittico solo se essi fossero del tutto isolati nell'universo. Ma il Sistema Solare è formato da numerosissimi corpi celesti: pianeti, satelliti, asteroidi, comete... studiando le perturbazioni del moto lunare a causa di questi corpi, e le conseguenti deviazioni dall'orbita perfettamente ellittica, è possibile determinarne la massa.

Venere vista dalla finestra di casa mia il 4 aprile 2020
.
2.7 Alla ricerca del pianeta sconosciuto
Del resto, lo studio delle perturbazioni dei moti planetari ha condotto nel passato a scoperte eccezionali. Quando infatti nel 1821 l'astronomo francese Alexis Bouvard (1767-1843) pubblicò il primo studio dei parametri orbitali di Urano, tutti si resero conto che esso deviava in maniera evidente dalle previsioni teoriche della legge (2.6): in alcuni momenti sembrava muoversi lungo la propria orbita più velocemente di quanto previsto, in seguito rallentava inaspettatamente. Alcuni cominciarono a chiedersi se la Legge di Gravitazione Universale fosse davvero universale, o piuttosto cessasse di valere a così grande distanza dal Sole. Ma l'astronomo francese Urbain Le Verrier (1811-1877) e il matematico inglese John Couch Adams (1819-1892) avevano fede nelle scoperte di Newton, e supposero che le irregolarità nel moto di Urano fossero dovute alla presenza di un altro corpo celeste di notevoli dimensioni che orbitava al di là di Urano. Come sappiamo, in base alla Terza Legge di Keplero, più un pianeta è lontano dal Sole, più orbita lentamente; dunque Urano è più veloce di questo fantomatico ottavo pianeta, e lo supera lungo la sua orbita. Quando Urano si sta avvicinando ad esso, quest'ultimo lo attira e fa sì che si muova più velocemente del previsto; quando Urano lo ha superato, esso lo rallenta con la propria attrazione. Lavorando indipendentemente fra loro, Le Verrier ed Adams compirono una serie di noiosi calcoli, supponendo pianeti diversi a diverse distanze; Adams spedì i suoi studi all'astronomo britannico George Airy (1801-1892), suggerendo la posizione in cui avrebbe dovuto trovarsi questo nuovo pianeta, ma egli ignorò e cestinò il tutto. Per fortuna Le Verrier spedì invece i propri risultati all'Osservatorio di Berlino, dove Johann Gottfried Galle (1812-1910) e il suo discepolo Heinrich Ludwig d'Arrest (1822-1875) nella notte del 23 settembre 1846 puntarono il telescopio nella regione di cielo indicata da Le Verrier, e dopo appena mezz'ora, a meno di un grado dalla posizione prevista dal francese, individuarono l'ottavo pianeta, da loro battezzato Nettuno, per il suo caratteristico colore azzurro, che ricordava quello del mare. In seguito si scoprì che il pianeta era già stato osservato al telescopio da Galileo Galilei il 27 dicembre 1612, e da questi scambiato per una stella.


I pianeti Urano (a sinistra) e Nettuno (a destra) visti dal telescopio Hubble
In seguito Le Verrier, galvanizzato dal successo, si lasciò prendere la mano, e suppose che le irregolarità nel moto del nuovo pianeta scoperto avrebbero consentito la scoperta di un nuovo pianeta, e queste di un altro ancora, e così via. Siccome anche il moto di Nettuno sembrava presentare delle deviazioni da quanto previsto dalla Legge di Newton, e siccome non tutte le anomalie di Urano erano spiegabili attraverso l'esistenza di Nettuno, cominciò la ricerca sistematica di un nono pianeta del Sistema Solare. Le Verrier morì senza aver avuto la soddisfazione di trovarlo, e così della ricerca si incaricarono gli astronomi statunitensi William Henry Pickering (1858-1938) e Percival Lowell (1855-1916). Essi utilizzavano un metodo diverso da quello dei loro predecessori: scattavano a distanza di tempo delle fotografie della stessa regione di cielo, e poi, confrontando le lastre, studiavano se qualche immagine su di esse si muoveva rispetto alle stelle fisse, segno certo del fatto che doveva trattarsi di un asteroide, una cometa o un pianeta. Per decenni, tuttavia, la ricerca non diede alcun risultato. Solo il 18 febbraio 1930, l'astronomo americano Clyde Tombaugh (1906-1997) scoprì un nuovo corpo celeste nella posizione calcolata da Lowell. Come racconta lo youtuber e divulgatore scientifico Adrian Fartade nei suoi libri, il pubblico da ogni parte del mondo mandò all'osservatorio Lowell svariate proposte per il nome ufficiale del nuovo pianeta; c'erano nomi ispirati alla mitologia come Minerva, Osiride o Giunone; altri ispirati alla modernità, come Elettricità; alcuni erano semplicemente strani o divertenti, come Zyxmal, proposto con la seguente motivazione: « È l'ultima parola nel dizionario, e questo è l'ultimo dei pianeti ». La vedova di Percival Lowell propose prima di chiamarlo Percival o Lowell, in onore del marito e fondatore dell'osservatorio, ma poi arrivò a proporre Constance in onore di se stessa. Alla fine venne accettata la proposta di una bambina inglese di 11 anni, Venetia Burney (1918-2009), appassionata di mitologia, che propose Plutone perché è un mondo molto lontano dal Sole, posto quasi nell'oltretomba, e perchè le sue prime due lettere sono le iniziali di Percival Lowell. E Plutone fu. Il pianeta fu in seguito rintracciato in fotografie risalenti al 19 marzo 1915.
Plutone era stato trovato quasi esattamente nella posizione prevista dai calcoli teorici, per cui inizialmente si credette di aver trovato il corpo celeste in grado di perturbare Urano e Nettuno. Con il passare degli anni, tuttavia, le misurazioni effettuate rivelarono che Plutone era di gran lunga troppo piccolo per spiegare le perturbazioni osservate, e si pensò quindi che non si potesse trattare dell'ultimo pianeta del Sistema Solare, ma che esistesse un decimo pianeta delle dimensioni di Urano e Nettuno. Partì così la caccia al fantomatico pianeta, che fu battezzato provvisoriamente Pianeta X: un gioco di parole basato sul fatto che X è il numero romano di valore 10, ma anche il simbolo dell'incognito. Le ricerche durarono oltre cinquant'anni, ma senza esito. La certezza dell'esistenza di questo mondo era tale che la famosa serie a cartoni animati "Danguard" ruota appunto attorno alla ricerca di un decimo pianeta del Sole, chiamato Prometeo.
Ma negli anni settanta fu lanciata la sonda americana Voyager 2 la quale, sfruttando un raro allineamento planetario, visitò in sequenza Giove, Saturno, Urano e Nettuno, spedendo a terra eccezionali fotografie di quei mondi remoti. Ebbene, nel 1989 l'analisi dei dati della sonda Voyager 2 rivelò che le misure della massa di Urano e Nettuno comunemente accettate in precedenza erano lievemente sbagliate. Le orbite calcolate con le nuove masse non mostravano alcuna anomalia, il che escludeva categoricamente la presenza di qualunque gigante gassoso più esterno di Nettuno. La scoperta di Plutone fu insomma casuale, trovandosi quel corpo celeste al posto giusto nel momento giusto, mentre si dava la caccia a qualcosa d'altro. Un tempo si era ipotizzato che Plutone potesse essere un satellite di Nettuno andatosene per conto suo, dato che si trova in risonanza orbitale con esso 2 : 3 (cioè ogni due orbite di Plutone, Nettuno ne percorre tre); oggi invece sappiamo che si formò con il materiale più esterno della nebulosa solare, insieme a molti altri corpi ghiacciati ad esso simili. Il 24 agosto 2006 Plutone fu declassato da pianeta a pianeta nano, mentre il 14 luglio 2015, alle ore 13.49 italiane, la sonda NASA "New Horizons" ha sorvolato Plutone a una quota di 12.500 chilometri, rivelando tra l'altro che esso è leggermente più grosso di quanto si pensasse.


A
sinistra: Plutone ripreso dalla sonda New Horizons.
A destra: il
cane di Topolino fu battezzato Pluto perchè
venne ideato poche settimane dopo la scoperta di Plutone!
Attenzione però, perchè Plutone non è l'estremo confine del sistema solare. Si conoscono ormai molti oggetti che orbitano al di là di essa, tutti remoti e freddissimi, come Eris, Quaoar, Orco e Sedna. Attualmente il corpo celeste conosciuto del sistema solare più lontano dalla sua stella è un oggetto scoperto presso l'osservatorio di Mauna Kea nel gennaio 2018 e annunciato in una conferenza stampa il 21 febbraio 2019 dagli astronomi Scott Sheppard, David Tholen e Chad Trujillo, che lo hanno soprannominato "FarFarOut" (in inglese "molto molto lontano") per sottolineare la sua estrema distanza dal Sole. L'Unione Astronomica Internazionale ha attribuito all'oggetto la designazione provvisoria 2018 AG37, in attesa dell'assegnazione di un nome mitologico com'è abitusine. Esso ha una magnitudine apparente molto debole di +25, tanto che solo i più grandi telescopi del mondo possono osservarlo: i suoi dati sono ancora molto incerti, essendo necessario un arco di osservazione di diversi anni per determinarle con maggior precisione, ma si pensa che il perielio si trovi a 27,06 ± 5,24 unità astronomiche (4,14 ± 0,79 miliardi di chilometri) dal Sole, e il suo afelio addirittura a 144,94 ± 114,0 unità astronomiche (22 ± 17 miliardi di chilometri). Attualmente si pensa che si trovi a 132,2 ± 1,5 unità astronomiche (19,78 ± 0,22 miliardi di chilometri) dal Sole, mentre e il suo periodo di rivoluzione è molto incerto, ma potrebbe oscillare tra gli 800 e i 1000 anni. Vista la sua enorme distanza da noi, 2018 AG37 si muove molto lentamente tra le stelle di sfondo ed è stato osservato solo 9 volte in 2 anni!
Eppure, il sistema solare non è ancora giunto al capolinea con 2018 AG37. Al di là di esso infatti si stenderebbe la nube di Oort, una vasta regione sferica del sistema solare esterno che si estenderebbe da 10.000 fino a più di 100.000 unità astronomiche (da 0,15 ad oltre 1,5 anni luce) dal Sole, ipotizzata nel 1932 dall’astronomo estone Ernst Öpik (1893-1985), che per primo formulò una teoria sull’origine delle comete nel sistema solare, e nel 1950 dall’astronomo olandese Jan Oort (1900-1992). Essi ritenevano che le comete avessero origine in una nube che orbitava ben oltre l’orbita di Plutone, costituita da un gran numero di oggetti celesti ghiacciati, principalmente comete, che orbitano intorno al Sole a distanze estremamente grandi, fino a diverse migliaia di unità astronomiche. In particolare la nube di Oort (ma sarebbe più giusto chiamarla di Öpik-Oort) è considerata uno dei possibili serbatoi delle comete a lungo periodo, che impiegano migliaia o addirittura milioni di anni per completare un’orbita intorno al Sole. Quando le interazioni gravitazionali con altre stelle o con oggetti trasnettuniani spingono una cometa da questa remota regione verso il Sole, la sua orbita può portarla a passare vicino alla Terra, rendendola visibile come una cometa con tanto di coda. Tuttavia, poiché la nube di Oort è situata a così grande distanza e ha una densità estremamente bassa, non è ancora stata osservata direttamente, e si pensa che difficilmente lo sarà anche in futuro: le informazioni che abbiamo sulla sua esistenza e sulla sua composizione derivano principalmente da modelli teorici e da osservazioni di comete che si pensa provengano da quella regione. Secondo alcuni in essa potrebbero essere nascosti dei pianetini rocciosi, come Sedna, un freddo planetoide scoperto il 14 novembre 2003 e grande forse i due terzi di Plutone: esso infatti ruota attorno al Sole su di un'orbita particolarmente eccentrica che lo porta ad avvicinarsi al Sole fino a 76 unità astronomiche (11,4 miliardi di chilometri) al perielio, che raggiungerà il 18 luglio 2076, e ad allontanarsi da esso fino ad 897 unità astronomiche (oltre 5 giorni luce!) dal Sole all'afelio. Per percorrere tale orbita allungatissima, Sedna impiega almeno 10.737 anni! I suoi scopritori sostengono che Sedna, che prende il nome dalla dea del mare della mitologia Inuit, sia il primo corpo della nube di Öpik-Oort ad essere osservato. I modelli teorici tuttavia hanno mostrato che è difficile che un corpo con queste caratteristiche si sia formato laggiù: è più probabile cioè che sia nato più vicino al Sole, e che qualcosa lo abbia attratto nell'orbita attuale.
La scoperta di altri due strani corpi celesti simili a Sedna, Leleākūhonua e 2012 VP113 (per questi remoti corpi ghiacciati è stato coniato il termine sednoidi), ha spinto Chad Trujillo e Scott Sheppard a proporre la possibile esistenza di una massa planetaria invisibile più lontana, informalmente chiamata "il Pianeta Nove" (per analogia con l'antico Pianeta X), delle dimensioni di Nettuno, che avrebbe attratto laggiù i corpi di questo tipo. Si è scoperto che i sednoidi lontanissimi dal Sole seguono orbite ellittiche che dovrebbero essere orientate in qualsiasi direzione, ed invece sembrano avere un allineamento particolare: tutti gli assi maggiori delle loro orbite sono approssimativamente allineati, e condividono anche un angolo simile di inclinazione rispetto all'orbita terrestre: la probabilità di un allineamento del genere in un campione così piccolo è inferiore all'uno per cento. Il responsabile di questa stranezza potrebbe essere effettivamente un oggetto planetario di massa superiore a dieci volte quella della Terra. Con il tempo sono emerse altre prove indirette dell'esistenza del Pianeta Nove, in particolare una leggera inclinazione dell'asse di rotazione del Sole, nessuna delle quali è conclusiva, ma tutte abbastanza bizzarre da spingere gli astronomi a cercarne un responsabile. Tutto ciò ha reso di nuovo attuale la caccia al fantomatico Pianeta X, anche se esso ha cambiato nome. Per cercare di osservarlo direttamente, gli astronomi hanno passato al setaccio diversi monitoraggi del cielo alla ricerca di quella che sarebbe la scoperta astronomica più importante del XXI secolo. Non si trattava di un compito semplice: inizialmente hanno trovato 1,3 miliardi di oggetti, ma usando varie tecniche sono riusciti a ridurli a soli 244 milioni. L'elaborazione ha comunque richiesto mesi di calcolo al computer. Finora la ricerca non ha dato alcun esito, eliminando il 78 % dei possibili "nascondigli" del Pianeta Nove. Ciò riduce la probabilità che il presunto pianeta esista, ma il 22 % del cielo in cui potrebbe ancora nascondersi abbraccia una grande porzione di cielo che si affaccia sul piano della nostra galassia, la Via Lattea, dove le stelle sono molto più affollate, rendendo la ricerca più difficile. La scoperta di un nuovo sednoide, 2017 OF201, avvenuta il 23 luglio 2017 ad opera di Sihao Cheng dell’Institute for Advanced Study, in collaborazione con Jiaxuan Li ed Eritas Yang della Princeton University, ha rimesso in discussione l'esistenza del pianeta fantasma, perchè questo sednoide (candidato al titolo di pianeta nano con un dianetro stimato di 700 km) presenta un’orbita altamente eccentrica, con un perielio a circa 44,9 UA e un afelio che si estende fino a circa 1600 UA, così ampia da richiedere almeno 25.000 anni per compiere una rivoluzione completa, ma che non si allinea affatto con quella degli altri sednoidi, suggerendo che potrebbe non essere affatto influenzata dalla gravità di un ipotetico nono pianeta. L'Osservatorio "Vera Rubin", entrato in funzione a giugno 2025, sarà in grado di effettuare ricerche efficienti anche nei punti del cielo più difficili, chiarendo forse se questo fantomatico pianeta esiste o se si tratta, come per il Pianeta X, di un'elegante teoria non confermata dalle osservazioni.
.
2.8 Due masse o una sola?
Prima di passare oltre, è indispensabile affrontare un importantissimo problema. Infatti, noi abbiamo affermato che la forza di gravità è direttamente proporzionale alle masse dei corpi. Ma questa forza agisce tra le masse anche se esse sono inizialmente in quiete; invece, la massa di un corpo è stata definita, sulla base delle leggi del moto, come una misura dell'inerzia che ogni corpo oppone allo spostamento. Per questo la si chiama anche massa inerziale (mi). Quella che noi abbiamo introdotto invece è una grandezza analoga alla carica elettrica, che per le leggi di Coulomb esercita una forza su un'altra carica: Newton insomma tratta della "carica" che esercita su un'altra "carica" la forza di gravitazione, e che andrebbe più propriamente chiamata massa gravitazionale (mg). La (2.6) quindi andrebbe più esattamente così riscritta:

Dobbiamo dunque essere certi che le due masse possano essere identificate tra loro. Possiamo rendercene conto semplicemente analizzando il problema da noi risolto nel § 2.4. Infatti, noi abbiamo uguagliato la forza gravitazionale, che contiene la massa gravitazionale, e la forza peso, che contiene la massa inerziale:

e abbiamo semplificato le masse. Se ciò non fosse possibile, se cioè mi e mg fossero diverse tra loro, la (2.7) andrebbe così riscritta:

Ma non ci sarebbe motivo per cui il rapporto ( mg / mi ) sia costante per tutti i corpi; per cui, il valore di g non sarebbe indipendente dal corpo, e noi dovremmo osservare un'accelerazione di gravità diversa da corpo a corpo! Il fatto che questo non corrisponda alla realtà sperimentale ci dice che il rapporto è costante per tutti i corpi. Allora, con un opportuno cambiamento nel sistema di misura, posso fare in modo che tale rapporto valga uno. D'ora in poi, perciò, potremo chiamare semplicemente "massa" il termine m che compare nella (2.6)! Di questo argomento ci varremo nel § 6.3 per introdurre il Principio di Equivalenza.
.
2.9 I punti lagrangiani
Per concludere, vogliamo fare un accenno al cosiddetto problema dei tre corpi. Esso consiste nel calcolare, date la posizione iniziale, la massa e la velocità di tre corpi soggetti alla reciproca attrazione gravitazionale, l'evoluzione del sistema da essi costituito. Contrariamente alle apparenze, il problema è tutt'altro che semplice; anzi, fin da principio si accorse che le equazioni risolventi, scritte sulla base delle leggi del moto e dell'equazione di Newton, non possono essere "portate alle quadrature", cioè risolte esplicitamente per via analitica; soluzioni più o meno semplici si possono trovare soltanto in casi particolari. Delle soluzioni approssimate possono essere trovate con il cosiddetto "metodo delle perturbazioni", cioè introducendo di volta in volta delle variazioni molto piccole dei parametri. Oggi inoltre è possibile ottenere soluzioni di tipo numerico con la precisione voluta, utilizzando dei calcolatori elettronici. In ogni caso, affrontando il problema dei tre corpi si scopre che il risultato trovato è valido solo per un determinato lasso di tempo, oltre il quale il risultato diverge dal comportamento del sistema in modo imprevedibile: in altre parole, il sistema è di tipo caotico. Proprio la ricerca di soluzioni approssimate del problema dei tre corpi si giunse a mettere a punto la moderna Teoria del Caos, e in particolare il cosiddetto Caos Deterministico.

Tra i principali autori ad interessarsi del problema dei tre corpi ci furono Joseph-Louis Lagrange (1736-1813), Henri Poincaré (1854-1912) e il nostro Tullio Levi-Civita (1873-1941). In particolare, Lagrange dimostrò che, nel caso di tre corpi di cui due si muovono di moto circolare rispetto al terzo, e uno dei due ha massa trascurabile, esistono cinque punti di equilibrio su cui quest'ultimo può trovarsi. Tali punti sono detti punti lagrangiani. Tre di essi giacciono sulla stessa retta dei due corpi maggiori, uno compreso tra essi e due esterni, ma queste posizioni sono instabili. Gli altri due punti sono invece posti sull'orbita del corpo in moto di massa non trascurabile, uno in anticipo e l'altro in ritardo di 60° rispetto a questi. In altre parole, in questo caso i segmenti che congiungono i tre corpi formano due triangoli equilateri. Se il rapporto tra le masse dei due corpi maggiori è sufficientemente elevato, questi ultimi due punti di equilibrio sono stabili e gli oggetti di massa trascurabile situati in questa posizione orbitano stabilmente intorno al corpo maggiore. È il caso di Giove, che viene seguito e preceduto lungo la sua orbita da due gruppi di asteroidi detti Troiani, essendo intitolati agli eroi omerici della Guerra di Troia. Per la precisione esistono due gruppi di satelliti Troiani di Giove: i Troiani del Campo Greco, come 588 Achilles (di circa 135,5 km di diametro, scoperto il 22 febbraio 1906 dall'astronomo tedesco Max Wolf), precedono Giove di 60° sulla sua orbita, in prossimità del punto L4, mentre i Troiani del Campo Troiano, come 884 Priamus (scoperto sempre da Max Wolf il 22 settembre 1917), seguono di 60° Giove sulla sua orbita, in prossimità del punto L5. Degli esempi si ritrovano anche nel sistema di satelliti di Saturno, la cui luna Teti condivide l'orbita con due piccolissime lune, Telesto e Calipso, situate nei punti lagrangiani della sua orbita; anche Dione, il satellite immediatamente più esterno, condivide l'orbita con la piccolissima luna Elena in uno dei suoi punti lagrangiani. Recentemente sono stati scoperti i Troiani di Nettuno, e il 1 ottobre 2010 è stato scoperto il primo asteroide troiano della Terra, 2010 TK7, di appena 300 metri di diametro, che precede il nostro pianeta nella sua orbita attorno al Sole.
Gli altri tre punti di Lagrange, come detto, sono instabili, ma proprio L1 ed L2 sono i più interessanti per le missioni spaziali umane, e il perchè è presto detto. Il punto Ll si trova circa 1,5 milioni di chilometri all'interno dell'orbita terrestre, sulla linea che unisce la Terra e il Sole. È la posizione ideale per i satelliti che devono tenere sotto costante osservazione la nostra stella, come il satellite SOHO della NASA. Anche il punto L2 si trova a 1,5 milioni di chilometri di distanza dalla Terra, ma dalla parte opposta a Ll rispetto al nostro pianeta. È il punto giusto per porre un osservatorio spaziale, avendo sia la Terra sia il Sole costantemente dallo stesso lato, ed il vantaggio è duplice: una porzione molto grande del cielo sarà sempre sgombra per le osservazioni, ed uno scudo fisso potrà schermare facilmente il satellite dal disturbo elettromagnetico da parte dei due corpi celesti. Per questo, L2 è stato scelto per piazzare nello spazio il grande telescopio spaziale "James Webb", lanciato il 25 dicembre 2021, ma anche missioni spaziali passate come WMAP e Planck. Naturalmente diversi satelliti possono condividere la stessa regione dello spazio perché non si trovano esattamente nello stesso punto, ma gli girano attorno lungo un'orbita ellittica. E, altrettanto naturalmente, si tratta di punti di equilibrio instabile. Ciò significa che, se si vuole mantenere un satellite in quella posizione, quindi, bisogna di tanto in tanto spendere energia, il che mette un limite alla durata delle missioni spaziali, inclusa quella del pur costosissimo "James Webb".
Invece L3 si trova nel punto dell'orbita terrestre diametralmente opposto rispetto al Sole. Esso dunque è perennemente nascosto alla nostra vista dietro alla nostra stella. Sarebbe il posto ideale per porvi una stazione spaziale segreta, che risulterebbe completamente invisibile dal nostro pianeta, molto più della famosa base degli uomini di Vega sulla faccia nascosta della Luna nel celebre anime "Atlas Ufo Robot". I punti L4 ed L5 infine, essendo di equilibrio stabile come si è visto sopra, sono poco adatti ad ospitare satelliti artificiali, dato che polvere e asteroidi finiscono per addensarsi in essi, costituendo un grave pericolo per i delicatissimi e costosissimi avamposti umani nello spazio.
Chiudiamo questo capitolo con un meme particolarmente divertente:

.
A questo punto, sento già la vostra domanda: ma cos'è questo "campo gravitazionale" di cui tanto spesso si sente parlare? Cliccate qui per proseguire il vostro viaggio, e lo saprete! Per tornare all'indice, invece, il link è questo.
![]()