![]()
|
« Egli si presenterà davanti al sacerdote Eleazaro, che consulterà per lui il giudizio degli urim davanti al Signore... » (Num 27, 21) |
Uno dei misteri più fitti intorno all'Antico Testamento in realtà non riguarda né la data della Creazione, né la realtà storica del Diluvio Universale, né tantomeno i misteriosi codici che secondo alcuni sarebbero nascosti nel testo greco della Torah. Assai più misteriosa, in realtà, è la natura di alcuni oggetti che ebbero un ruolo importante nell'antica storia di Israele, e di cui oggi praticamente conosciamo soltanto i nomi: stiamo parlando degli Urim e Tummim (in ebraico Urim VeTumim, אורים ותמים). E persino i loro nomi sono trascritti di volta in volta in modi diversi (per esempio Thummim o Thummin). Li sentiamo nominare per la prima volta nel libro dell'Esodo, quando il Signore dà disposizioni a Mosè circa le norme liturgiche del Suo culto:
« Unirai al pettorale del giudizio gli Urim e i Tummim. Saranno così sopra il cuore di Aronne quando entrerà alla presenza del Signore: Aronne porterà il giudizio degli Israeliti sopra il suo cuore alla presenza del Signore, per sempre. » (Es 28, 30)
Questi enigmatici oggetti dunque sembrano far parte integrante dell'abbigliamento del Sommo Sacerdote. Li ritroviamo infatti nell'investitura dei sacerdoti e nell'inaugurazione del culto da parte di Mosè:
« Mosè fece accostare Aronne e i suoi figli e li lavò con acqua. Poi rivestì Aronne della tunica, lo cinse della cintura, gli pose addosso il manto, gli mise l'efod e lo cinse con la cintura dell'efod, con la quale lo fissò. Gli mise anche il pettorale, e nel pettorale pose gli Urim e i Tummim. » (Lv 8, 6-8)
Inoltre, poco prima della morte di Mosè, quando il bastone del comando sta per passare a Giosuè, così parla Iddio:
« Il Signore disse a Mosè: "Prenditi Giosuè, figlio di Nun, uomo in cui è lo spirito; porrai la mano su di lui, lo farai comparire davanti al sacerdote Eleazaro e davanti a tutta la comunità, gli darai i tuoi ordini sotto i loro occhi e porrai su di lui una parte della tua autorità, perché tutta la comunità degli Israeliti gli obbedisca. Egli si presenterà davanti al sacerdote Eleazaro, che consulterà per lui il giudizio degli urim davanti al Signore; egli e tutti gli Israeliti con lui e tutta la comunità usciranno all'ordine di Eleàzaro ed entreranno all'ordine suo." » (Num 27, 18-21)
Anche la benedizione finale di Mosè alla tribù di Levi (la sua) nomina questi misteriosi accessori:
« Per Levi disse: "Dà a Levi i tuoi tummìm e i tuoi urìm all'uomo a te fedele, che hai messo alla prova a Massa, per cui hai litigato presso le acque di Merìba" » (Dt 33, 8)
Ma è solo quando si parla del Re Saul che vuole conoscere in anticipo l'esito della sua guerra contro i Filistei, che si accenna al reale scopo di questi aggeggi:
« Saul consultò il Signore e il Signore non gli rispose, né attraverso i sogni né mediante gli urìm né per mezzo dei profeti. » (1Sam 28, 6)
Appare chiaro che questi termini designavano una tecnica divinatoria usata dagli antichi Ebrei per interpretare il volere di Dio. Infatti si pensa che Tummim derivi dalla radice semitica tmm, che significa "innocente", mentre Urim si fa tradizionalmente derivare dal termine ebraico Arrim, con il significato di "maledizione"; quindi Urim e Tummim sostanzialmente significherebbero "maledetto [cioè colpevole] o innocente?" (il punto di domanda l'ho aggiunto io). Altri studiosi invece hanno suggerito un'etimologia che rimanda a due parole della lingua accadica, urtu e tamitu, che significano rispettivamente "oracolo" e "comando", il che porta acqua al mulino della nostra interpretazione. Per comprendere il significato di tale tecnica di divinazione ci conviene utilizzare come chiave interpretativa questo famoso brano del Primo I Libro di Samuele:
« Allora Saul disse: "Accostatevi qui, autorità tutte del popolo. Cercate ed esaminate da chi sia stato commesso oggi il peccato, perché per la vita del Signore, salvatore d'Israele, certamente costui morirà, anche se si trattasse di mio figlio Gionata". Ma nessuno del popolo gli rispose. Perciò disse a tutto Israele: "Voi state da una parte e io e mio figlio Gionata staremo dall'altra". Il popolo rispose a Saul: "Fa' quanto ti sembra bene". Saul disse al Signore: "Dio d'Israele, dà una risposta chiara". E furono indicati Gionata e Saul, mentre il popolo restò libero. Saul soggiunse: "Tirate a sorte tra me e mio figlio Gionata". E fu indicato Gionata. » (1 Sam 14, 38-42)
Esso descrive chiaramente il tentativo di identificare il peccatore attraverso la divinazione, dividendo ripetutamente le persone in due gruppi ed identificando in quale dei gruppi si trova il peccatore. Apparentemente il caso è indipendente dalla volontà umana, ma nella mentalità antica non era indipendente dalla volontà divina, che tutto può controllare, influendo così sul risultato del sorteggio. Come dunque interrogare il volere del Signore, dato che Egli non comunica con gli uomini a parole? Semplicemente chiedendogli di esprimere tale Suo volere manipolando un'estrazione a sorte, non dissimile in linea di principio dal nostro lancio della moneta. Per questo, anche se la natura esatta degli Urim e Tummim resta oscura, la maggior parte degli esegeti vede in essi degli oggetti da gettare. Dalle citazioni di Esodo e Numeri sopra riportate si può ipotizzare che fossero pietre che decoravano il pettorale del Sommo Sacerdote, che erano amovibili, e che, secondo una possibile traduzione, "servivano per" Urim e Tummim. La forma plurale, testimoniata dalla desinenza ebraica -im, probabilmente non indica che si trattava di gruppi di pietre, ma semplicemente evidenzia la loro importanza, com'è tipico delle lingue semitiche.
Del resto, perfino nel Nuovo Testamento si accenna a questo modo di interpretare il volere divino, quando si tratta di sostituire Giuda Iscariota nel novero degli Apostoli, per riportarli al numero di dodici, lo stesso delle Tribù di Israele. Oggi nessuno si sognerebbe di scegliere il nuovo Arcivescovo di Milano tirando a sorte fra più candidati; eppure, ecco cosa dice San Pietro, a testimonianza di quanto fosse radicata questa tradizione nell'Antico Israele:
« "Bisogna che, tra coloro che sono stati con noi per tutto il tempo nel quale il Signore Gesù ha vissuto fra noi, cominciando dal battesimo di Giovanni fino al giorno in cui è stato di mezzo a noi assunto in cielo, uno divenga testimone, insieme a noi, della sua risurrezione." Ne proposero due: Giuseppe detto Barsabba, soprannominato il Giusto, e Mattia. Poi pregarono dicendo: "Tu, Signore, che conosci il cuore di tutti, mostra quale di questi due tu hai scelto per prendere il posto in questo ministero e apostolato, che Giuda ha abbandonato per andarsene al posto che gli spettava". Tirarono a sorte fra loro e la sorte cadde su Mattia, che fu associato agli undici apostoli.» (Atti 1, 21-26)
In effetti, tutti i casi che abbiamo visto finora si possono ricondurre a domande poste alla Divinità, la cui risposta è semplicemente « Sì » o « No », esattamente come la testa e la croce di una moneta: un gruppo tra due in cui si trova il colpevole, o un candidato tra due da annoverare tra gli Apostoli. Nell'Antico Testamento si trovano solo due casi, in cui la domanda posta al Signore è più complicata, una sempre nel Primo Libro di Samuele, quando Saul viene designato Re proprio dalla sorte:
« Allora consultarono di nuovo il Signore: "È venuto qui quell'uomo?" Disse il Signore: "Eccolo nascosto in mezzo ai bagagli." » (1 Sam 10, 22)
E l'altra quando Davide, appena eletto a sua volta Re, attacca i Filistei:
« I Filistei salirono di nuovo e si sparsero nella valle dei Refaìm. Davide consultò il Signore, che gli rispose: "Non salire; gira alle loro spalle e raggiungili dalla parte di Becaìm. Quando sentirai un rumore di passi sulla cima di Becaìm, lanciati subito all'attacco, perché allora il Signore uscirà davanti a te per colpire l'accampamento dei Filistei". Davide fece come il Signore gli aveva ordinato e colpì i Filistei da Gàbaon fino all'ingresso di Ghezer. » (2 Sam 5, 22-25)
Nel primo caso però si può pensare che alla domanda "È venuto qui quell'uomo?" il Signore attraverso gli Urim e Tummim abbia risposto di sì, e poi la Tribù di Beniamino (cui Saul apparteneva) sia stata suddivisa in due gruppi per volta, fino a che non venne tirato a sorte quello che custodiva i bagagli. Nel secondo caso, invece, forse l'articolata risposta del Signore non viene dagli Urim e Tummim, ma da una voce profetica; oppure anche in questo caso la risposta originaria era costituita da una sequenze di "sì" e "no", ma la successiva rielaborazione del testo da parte dell'Autore Deuteronomista la ha trasformata in una sorta di risposta vocale, con tanto di indicazione del segnale convenuto (il rumore di passi).
Secondo alcuni esegeti poi neppure l'Autore dei passaggi biblici sopra riportati sapeva con certezza quale era la reale natura degli Urim e Tummim: forse non erano pietre visibili a tutti e amovibili dal pettorale del Sommo Sacerdote, ma poste all'interno di una specie di tasca, e quindi non visibili dall'esterno, perchè solo i Sacerdoti avevano diritto ad usarle (un po' come il tetragramma YHWH, del quale, a furia di non pronunciarlo, si finì per dimenticare quali erano le vere vocali). Ciò implica che Urim e Tummim fossero oggetti piccoli e quasi piatti; ed allora l'ipotesi più probabile è che fossero tavolette di legno o di osso. Appare possibile che il Sacerdote infilasse la mano nella tasca ed estraesse a caso uno dei due oggetti per confermare o negare un sospetto di colpevolezza: siccome (come si è appena detto) Urim significava sostanzialmente "colpevole" e Tummim sostanzialmente "innocente", se veniva estratto Urim, il responso era di colpevolezza, mentre se veniva estratto Tummim, il responso era di innocenza. Certi esegeti invece pensano a un'unica tavoletta con due facce, indistinguibili al tatto, delle quali una era chiamata Urim e l'altra Tummim; in tal caso l'ordalia consisteva nell'osservare quale delle due facce veniva estratta dalla tasca.

Ricostruzione moderna degli Urim e Tummim
Oggi alcuni storici pensano che gli Urim e Tummim derivino dalle cosiddette "Tavole dei Destini" delle religioni mesopotamiche, che stavano sul petto delle Sommo Sacerdote, e che venivano usate quando era in gioco il destino del re e della città (da cui il nome); il loro utilizzo era infatti basato sull'estrazione a sorte. Gli scrittori rabbinici classici sostenevano che Urim e Tummim potevano essere consultati solo da personaggi eminenti, come i generali dell'esercito, i più anziani dignitari di corte ed i re, e le sole domande che potevano essere poste erano quelle richieste a beneficio del popolo nel suo complesso. Con l'estinzione della monarchia e del culto del Primo Tempio, non è sorprendente che ogni memoria sulla forma e le modalità d'uso degli Urim e Tummim sia andata perduta. Giuseppe Flavio nelle "Antichità Giudaiche" sostiene che essi continuarono ad essere utilizzati fino all'epoca dei Maccabei, ma le fonti talmudiche sono unanimi nel sostenere che l'uso di Urim e Tummim venne abbandonato molto prima, quando Gerusalemme fu saccheggiata dai babilonesi di Nabucodonosor II. In due passi paralleli dei Libri di Esdra e di Neemia, si dice che a coloro che, dopo il ritorno da Babilonia, non erano in grado di dimostrare di essere discendenti da sacerdoti, fu chiesto di attendere fino a che non si fossero trovati sacerdoti in possesso di Urim e Tummim, e ciò conferma il punto di vista talmudico sulla perdita del loro utilizzo:
« Costoro cercarono il loro registro genealogico, ma non lo trovarono e furono allora esclusi dal sacerdozio. Il governatore disse loro che non potevano mangiare le cose santissime, finché non si presentasse un sacerdote con Urim e Tummim. » (Esdra 2, 62-63; Neemia 7, 64-65)
A dir la verità il Codice Sacerdotale, che risale ad un paio di secoli prima della cattività babilonese, non dice in nessun passo a che cosa assomigliavano Urim e Tummim, e non vi sono menzioni di Urim e Tummim da parte dell'Autore Deuteronomista oltre la morte di Davide, gli esegeti sospettano che l'uso degli Urim e Tummim fosse già stato abbandonato prima della conquista babilonese, forse come risultato dell'aumentata influenza dei profeti, che con la loro viva voce rendevano superfluo tirare a sorte per conoscere la volontà divina. Aggiungiamo che, secondo le fonti islamiche in nostro possesso, anche fra gli arabi era popolare una simile forma di divinazione prima della predicazione di Maometto due aste di freccia senza punta, su una delle quali era scritto "ordine" e sull'altra "divieto", erano poste in un contenitore e conservate nella Kaaba alla Mecca: ogni volta che qualcuno voleva sapere se sposarsi o intraprendere un viaggio, uno dei guardiani della Kaaba estraeva a caso una delle due aste di freccia dal loro contenitore, e la parola scritta su quella estratta indicava la volontà divina in merito alla domanda.
Da notare che un revival di questi strani dispositivi ha avuto luogo tra i Mormoni: il loro Joseph Smith (1805-1844) asserì di aver usato come "interpreti" per tradurre il Libro di Mormon delle pietre dorate fissate ad un pettorale e collegate in modo simile a quello di un paio di occhiali. Nel 1823 Smith disse che l'angelo Moroni, che gli aveva consegnato il Libro di Mormon inciso su tavole d'oro, gli aveva anche dato Urim e Tummim, « due pietre unite da una stanghetta di argento », aggiungendo che erano state predisposte da Dio per servire alla traduzione delle tavole d'oro. Smith affermò anche di aver utilizzato Urim e Tummim per ricevere altre rivelazioni divine; i Mormoni credono che gli Urim e i Tummim di Smith fossero identici a quelli biblici. Ci si potrebbe chiedere, a ragione, che cosa ci facevano Urim e Tummim nel continente americano, e poi proprio vicino a casa del "profeta" Smith, ma non è il caso di inoltrarci ulteriormente nella fede dei Mormoni. In tempi più vicini a noi, lo scrittore tedesco Thomas Mann (1875-1955) ha dissertato a lungo su Urim e Tummim in "Giuseppe il Nutritore", il quarto libro della sua tetralogia "Giuseppe e i suoi fratelli", mentre nel romanzo "L'Alchimista" di Paulo Coelho (1947-) il re di Salem dà al protagonista Santiago due pietre che chiama Urim e Tummim; una delle due è nera e le viene attribuito il significato di affermazione, mentre l'altra è bianca e significa negazione; questi significati sono applicabili quando vengono estratte da una borsa dopo che è stata loro rivolta una domanda appropriata. La leggenda di Urim e Tummim ha un'importanza di rilievo anche nel film "The Cutter - Il trafficante di diamanti" (2005) di Chuck Norris.
Ad ogni modo, è evidente che, da un punto di vista meramente scientifico, il presentarsi del responso "colpevole" o "innocente" al momento dell'estrazione di Urim e Tummim dalla tasca in cui erano riposti, è governato unicamente dal caso, né più e né meno del lancio dei moderni dadi. L'aggettivo "moderni" che ho appena utilizzato, però, può ingannare, dal momento che i nostri dadi sono quasi altrettanto antichi quanto gli ebraici Urim e Tummim. Il fatto che i dadi sono stati usati in tutto l'Oriente da tempo immemorabile è infatti dimostrato dai loro ritrovamenti in antiche tombe, che indicano chiaramente una loro origine Asiatica. I dadi si sono probabilmente evoluti dall'uso degli astragali, ossi del tarso che negli ungulati possiedono quattro facce facilmente distinguibili, ed oggi è certo che fossero già usati in tempi largamente antecedenti le prime attestazioni scritte da popoli molto lontani tra di loro, tra i quali anche gli Eschimesi, i Maya, le antiche popolazioni dell'Africa e i Polinesiani. Inizialmente erano considerati oggetti magici, utilizzati per divinare il futuro, e per questa ragione venivano conservati nelle tombe. Gli esemplari più antichi furono ritrovati nel 1972 all'interno di una tomba risalente al V millennio avanti Cristo; dadi a sei facce, praticamente uguali a quelli moderni, sono stati trovati in Cina (risalgono al 2000 a.C.) e in Egitto (600 a.C.). Il gioco dei dadi viene citato nei Rig-veda, nell'Atharvaveda e nella lista di giochi di Buddha; hanno inoltre un ruolo importante nel poema epico "Mahābhārata" dove Yudhisthira gioca a dadi contro Kaurava per il possesso del regno di Hastinapur facendo scoppiare una guerra. In Giappone, Cina, Corea, India e in altri paesi asiatici i dadi sono sempre stati popolari e lo sono tuttora: i segni sui pezzi del domino cinese si sono evoluti a partire dai segni sulle facce di due dadi affiancati, presi nelle loro varie combinazioni.
Venendo all'antica Grecia, dove dado si diceva "kubos", Sofocle riteneva che i dadi fossero stati inventati da Palamede, eroe della guerra di Troia figlio di Nauplio e Climene; Erodoto nelle "Storie" (I, 7) ne attribuiva l'invenzione agli abitanti della Lidia. I giochi d'azzardo con due o tre dadi erano una forma di divertimento nella Grecia antica, specialmente tra le classi superiori, quasi immancabile nei banchetti. I dadi più antichi ritrovati in Italia risalgono invece all'epoca etrusca: erano d'avorio, avevano sei facce ed erano ornati di lettere e non di numeri. Presso i Romani i dadi erano utilizzati soprattutto per i giochi d'azzardo, strettamente connessi con Saturno: a Roma era permesso giocare a dadi soltanto durante i Saturnali, i giorni dedicati al dio Saturno che rappresentavano l'equivalente romano del nostro carnevale. Anche il gioco della tombola risale a quel periodo: il "Grande Gioco di Saturno" era una sorta di gioco-oracolo con il quale anticamente si esercitava una forma di divinazione. Le scommesse sui dadi per denaro furono l'oggetto di molte leggi romane: una di queste imponeva che nessuna causa potesse essere intentata da una persona che permetteva il gioco d'azzardo nella sua casa. Questo gioco era così popolare tra i soldati che, al momento di oltrepassare con l'esercito il fiume Rubicone per marciare alla volta di Roma, nella notte del 10 gennaio del 49 a.C., Giulio Cesare esclamò: « alea iacta est! », cioè « il dado è tratto », come afferma lo storico Svetonio nel suo "De vita Caesarum". In tutti e quattro i Vangeli, poi, i soldati romani tirano a sorte le vesti di Gesù (Giovanni fa anche riferimento al Salmo 22, 19), ed è evidente che lo hanno fatto usando i dadi, perchè sul pavimento di quello che fu il Pretorio di Pilato nella Fortezza Antonia (il cosiddetto Litostroto, in ebraico Gabbatà, citato in Giovanni 19, 13) gli archeologi hanno ritrovato tracce delle incisioni fatte dai legionari romani che vi giocavano a dadi:
« Dopo averlo crocifisso, si divisero le
sue vesti, tirandole a sorte. » (Matteo 27, 35)
« Poi lo crocifissero e si divisero le sue vesti, tirando a sorte su di esse ciò
che ognuno avrebbe preso. » (Marco 15, 24)
« Gesù diceva: "Padre, perdona loro perché non sanno quello che fanno". Poi
dividendo le sue vesti, le tirarono a sorte. » (Luca 23, 34)
« I soldati poi, quando ebbero crocifisso Gesù, presero le sue vesti, ne fecero
quattro parti, una per ciascun soldato, e la tunica. Ma quella tunica era senza
cuciture, tessuta tutta d'un pezzo da cima a fondo. Perciò dissero tra loro:
"Non stracciamola, ma tiriamo a sorte a chi tocca". Così si compiva la
Scrittura, che dice: "Si sono divisi tra loro le mie vesti, e sulla mia tunica
hanno gettato la sorte." E i soldati fecero così. » (Giovanni 19, 23-24)
Qui sotto si vede l'incisione del cosiddetto "Gioco del Re", indicato dalla corona posta vicino alla lettera B (come Basileus, in greco "Re"). Questo gioco era in voga durante i Saturnali: veniva sorteggiato un condannato a morte, e veniva preso in giro come un re da burla, fino a che non veniva eseguita la condanna a morte del "re". Il simbolo dello scorpione indica la presenza nel Litostroto dei soldati della Legione X Fretense (da fretum, "stretto di mare", nome datogli per una battaglia vinta nello Stretto di Messina), che era di stanza a Gerusalemme negli anni della predicazione di Gesù, ed aveva proprio uno scorpione come suo emblema. Come si sa, il predicatore di Nazaret era accusato di essersi proclamato "re dei Giudei", e la cosa faceva sicuramente diventare il "Gioco del Re" ancora più divertente per i crudeli legionari della X Fretense, come lo descrivono gli evangelisti: « Lo spogliarono, gli fecero indossare un mantello scarlatto, intrecciarono una corona di spine, gliela posero sul capo e gli misero una canna nella mano destra. Poi, inginocchiandosi davanti a lui, lo deridevano: "Salve, re dei Giudei!" Sputandogli addosso, gli tolsero di mano la canna e lo percuotevano sul capo. » (Matteo 27, 28-30)

Il "Gioco del Re" sul Litostroto di Gerusalemme (da questo sito)
L'imperatore Claudio, noto intellettuale, scrisse un trattato sui dadi, che però non ci è pervenuto. Tacito affermò che i germani erano tanto appassionati del gioco dei dadi, che una volta perso tutto avrebbero messo in palio la loro libertà personale:
« Aleam, quod mirere, sobrii inter seria exercent, tanta lucrandi perdendive temeritate, ut, cum omnia defecerunt, extremo ac novissimo iactu de libertate ac de corpore contendant. Victus voluntariam servitutem adit: quamvis iuvenior, quamvis robustior adligari se ac venire patitur.
[È stupefacente vedere con quale serietà giochino ai dadi, e mai in condizioni di ubriachezza; l'azzardo e l'accanimento, vincano o perdano, sono tali che, una volta venuti meno tutti i loro beni, con un ultimo e decisivo colpo, pongono come posta la loro libertà personale. Chi perde, accetta volontariamente la schiavitù: può anche essere più giovane e robusto del vincitore, ma si lascia legare e mettere in vendita.] »
(Tacito, Germania, 24)
Il gioco dei dadi come lo conosciamo oggi nacque però durante il Medioevo, e in particolare al tempo delle crociate, sotto il nome di Hasard (o Hazard), che deriva dalla parola araba "Zahr", per l’appunto "dado" (da cui derivano sia la "zara" dantesca che il termine "azzardo"). Il gioco dei dadi venne esportato in Francia, dove esistevano vere e proprie corporazioni di giocatori di dadi, e in Germania, dove i temuti lanzichenecchi si guadagnarono la fama di grandi giocatori di dadi. Nella "Divina Commedia" Dante menziona il gioco della zara, che si giocava con tre dadi, e del quale abbiamo parlato in un altro ipertesto:
« Quando si parte il gioco de la zara,
colui che perde si riman dolente,
repetendo le volte, e tristo impara... » (Purg. VI, 1-3)
Dalla Francia poi questo passatempo venne portato in America, a New Orleans, prima città degli Stati Uniti dove il gioco d’azzardo cominciò la sua diffusione, attirando tantissimi appassionati. Negli Stati Uniti il gioco prese il nome di "craps" e venne regolamentato dal francese Bernard Xavier Philippe de Marigny de Mandeville (1785-1868); ancora oggi in America è uno dei giochi d’azzardo più amati, e lo si pratica in tutti i casinò, anche dopo che si è diffusa la moda dei casinò online. Infine, non possiamo chiudere questa breve carrellata senza citare la celeberrima affermazione di Albert Einstein: « Gott würfelt nicht », cioè « Dio non gioca a dadi »: con essa il genio tedesco intendeva rifiutare le conclusioni del Principio di Indeterminazione di Heisenberg, uno dei fondamenti della Meccanica Quantistica, secondo cui ogni evento ha una certa probabilità di accadere o meno. Einstein era invece convinto che ogni fenomeno fosse deterministico purché fosse possibile conoscere tutte le condizioni iniziali ed ogni forza coinvolta; alla sua asserzione, Niels Bohr rispose con un aforisma altrettanto noto: « Albert, smettila di dire a Dio cosa deve fare! »
L'importanza dei dadi nella storia della Matematica è tuttavia eccezionale, come testimonia il fatto che proprio dal latino "alea" (a sua volta ricavato dalla radice indoeuropea "as", "gettare", da cui anche il sanscrito "prasakas", "dado") deriva il termine "aleatorio"! Infatti proprio per risolvere problemi legati ai giochi con i dadi nacque il moderno Calcolo delle Probabilità. Il primo ad occuparsi di un'analisi matematica degli eventi casuali fu l'algebrista Gerolamo Cardano (1501-1576), che a quanto pare fu travagliato per tutta la vita dai problemi economici, e per risolverli si dedicò ai giochi d'azzardo. Per questo nel 1526 scrisse il "Liber de ludo aleae", che però fu pubblicato solo un secolo e mezzo dopo, nel 1663. Anche Galileo Galilei scrisse un libretto "Sulla scoperta dei dadi", pubblicato postumo nel 1656. La paternità del moderno calcolo delle probabilità è divisa equamente fra i francesi Blaise Pascal (1623-1662) e Pierre de Fermat (1601-1665); gli studi di Pascal presero avvio dai problemi che gli poneva uno dei suoi amici, il Cavaliere de Méré, accanito giocatore d'azzardo, il quale passò alla storia per essersi chiesto se era più probabile ottenere almeno un 6 in 4 lanci di un dado non truccato o almeno un doppio 6 in 24 lanci. Per risolvere tale quesito ed altri simili, Pascal avviò una corrispondenza con Fermat, dalla quale in una lettera del 29 luglio 1654 scaturì il concetto di probabilità come rapporto fra il numero di casi favorevoli ad un evento e il numero totale di casi possibili. Nel 1657 l'olandese Christiaan Huygens (1629-1695) scrisse il "Libellus de ratiociniis in ludo aleae", il primo vero trattato sul calcolo delle probabilità, che guarda caso chiama ancora in causa il gioco dei dadi, erede dei biblici Urim e Tummim.

I Peanuts alle prese con gli Urim e i Tummim! (striscia del 21 marzo 1979, da questo sito)
Si chiama variabile casuale o aleatoria una funzione che, ad ogni possibile esito di un esperimento aleatorio, associa un numero reale. Nel nostro caso, ricordando che l'utilizzo degli Urim e Tummim da parte del Sommo Sacerdote può sortire il valore T (Innocente, da Tummim) o U (Colpevole, da Urim), una variabile casuale può essere quella che associa all'evento T il numero di Tummim usciti su mille estrazioni. Un altro esempio di variabile casuale è quella che, ad una persona scelta a caso in una certa popolazione, associa la sua altezza; oppure quella che ad ogni molecola scelta a caso in un gas associa la sua velocità. Una variabile casuale X che assume un numero finito n di valori si dice discreta. Data una variabile casuale discreta che assume i valori x1, x2, ..., xn, a ciascuno degli eventi X = x1, X = x2, ..., X = xn si può associare la rispettiva probabilità.
Sia dunque una variabile casuale discreta che assume i valori x1, x2, ..., xn con probabilità rispettive p1, p2, ..., pn. Si dice distribuzione di probabilità della variabile casuale X la funzione che associa a ciascun xi la rispettiva probabilità pi (i = 1, 2, ..., n). Siccome gli eventi sono tra loro disgiunti e la loro unione rappresenta la totalità degli eventi possibili, ne segue che sarà sempre p1 + p2 + ... + pn = 1.
Si estraggano tre volte gli Urim e Tummim. Qual è la distribuzione di probabilità della variabile casuale che esprime il numero di Tummim ottenuti? Con la simbologia sopra introdotta io posso avere UUU (zero Tummim), TUU, UTU, UUT (un Tummim), TTU, TUT, UTT (due Tummim) o TTT (tre Tummim). Su otto casi totali, uno dà zero Tummim, tre ne danno uno, tre ne danno due e una ne dà tre, per cui potremo affermare che p(0) = 1/8, p(1) = 3/8, p(2) = 3/8 e p(3) = 1/8. Tabulando il tutto, la distribuzione di probabilità di questa variabile aleatoria sarà:
| xi |
0 |
1 |
2 |
3 |
| pi = X(xi) |
1/8 |
3/8 |
3/8 |
1/8 |
Si noti che si ha effettivamente 1/8 + 3/8 + 3/8 + 1/8 = 1.
Si chiama media, o valore atteso, o speranza matematica della variabile casuale X, e la si indica con μ o con E(X), il numero:
μ = x1 p1 + x2 p2 + ... + xn pn
Nel caso sopra considerato si ha:
μ = 0 x 1/8 + 1 x 3/8 + 2 x 3/8 + 3 x 1/8 = 12/8 = 1,5
In altre parole, estraendo un grandissimo numero di volte gli Urim e Tummim dalla tasca in cui il Sommo Sacerdote li conservava, ci aspettiamo di trovare in media 1,5 volte un verdetto di innocenza (Tummim).
Si dice invece varianza di X, e la si indica con σ2 o con V(X), il numero:
σ2 = x12 p1 + x22 p2 + ... + xn2 pn – μ2
Nel caso suddetto ad esempio si ha:
σ2 = 02 x 1/8 + 12 x 3/8 + 22 x 3/8 + 32 x 1/8 – (1,5)2 = 0,75
Si dice invece scarto quadratico medio o deviazione standard di X, e lo si indica con σ, la radice quadrata della varianza, che nel nostro esempio è la radice quadrata di 0,75, cioè 0,87. Il valor medio della variabile in questione potrebbe perciò essere scritto come < x > = 1,50 ± 0,87.
Tutto questo può essere applicato alla teoria dei giochi d'azzardo. Infatti un gioco si dice equo se, detta X la variabile casuale che rappresenta la somma complessiva vinta o persa dal giocatore al termine di una partita, si ha E(X) = 0. Se E(X) > 0, il gioco è favorevole al giocatore; se E(X) < 0, gli è sfavorevole.
Facciamo un esempio. Consideriamo i dadi con cui giocavano i soldati che crocifissero Gesù. Uno dei soldati lancia un dado; se esce un numero dispari, deve pagare due sesterzi. Se esce 2, vince 5 sesterzi. Se esce 4, non vince né perde nulla. Se esce 6, vince un sesterzio. Il gioco è equo? Chiamiamo X la variabile casuale che rappresenta la somma complessiva vinta o persa dal legionario. Se esce un numero dispari, evento che ha probabilità 3/6 = 1/2, si ha X = – 2. Se esce 2 (probabilità 1/6), X = + 5. Se esce 4 (probabilità 1/6), X = 0. Se esce 6 (probabilità 1/6), X = + 1. La distribuzione di probabilità allora è la seguente:
| X |
– 2 |
0 |
1 |
5 |
| p(X) |
1/2 |
1/6 |
1/6 |
1/6 |
Il valor medio di X è:
μ = – 2 x 1/2 + 0 x 1/6 + 1 x 1/6 + 5 x 1/6 = – 1 + 1/6 + 5/6 = 0
Si tratta dunque di un gioco equo: giocando un grande numero di volte, si può supporre che alla fine il soldato romano si troverà nella condizione iniziale, cioè non avrà guadagnato né perso nulla.

Antichi dadi ritrovati in una tomba etrusca
Facciamo ora un esempio moderno. Il gioco del lotto è equo? Consideriamo la probabilità di ottenere un ambo secco, cioè di azzeccare due numeri tra i cinque estratti su una certa ruota (i numeri totali sono 90). I casi possibili sono C90,5, cioè le combinazioni dei 90 numeri a 5 a 5, perchè l'ordine di estrazione non conta. Quanti sono casi favorevoli? Fissati i due numeri che io gioco, ad esempio 46 e 27, rispettivamente il numero dei libri dell'Antico e del Nuovo Testamento, restano da scegliere i restanti tre numeri, che possono venire estratti dai restanti 90 – 2 = 88 numeri. Ciò porta a C88,3 casi favorevoli (le combinazioni dei restanti 88 numeri a 3 a 3). La probabilità di azzeccare un terno secco è allora:
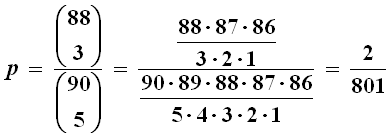
Se punto un euro sull'uscita di un certo ambo, quale dovrebbe essere la vincita equa in caso di vittoria? Sia X la somma complessiva. Se l'ambo non esce, perdo l'euro che ho puntato, e dunque X = – 1. Se l'ambo esce, avendo pagato un euro per la puntata, guadagno una somma che diremo S, quindi la vittoria netta è pari ad (S – 1). La distribuzione di probabilità è perciò:
| X | – 1 |
S – 1 |
| p(X) |
|
|
Se il gioco è equo, il valore atteso deve essere zero, e quindi:
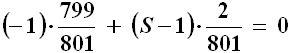
da cui si ricava S = 400,5. L'incasso equo per una puntata di un euro sarebbe dunque di 400,5 euro. Purtroppo l'ambo è pagato solo 250 volte la posta. Conclusione: chi gioca al lotto, a lungo andare, è sempre in perdita, e a vincere è solo lo Stato.
Consideriamo ora un evento casuale che può avere solo due possibili esiti, proprio come Urim o Tummim, figlio maschio o figlia femmina, radionuclide decaduto o non decaduto. In generale, come nel caso della divinazione ebraica, l'uno evento rappresenta un successo (l'innocenza), l'altro un fallimento (la colpevolezza). Sia dunque p la probabilità del successo; quella dell'insuccesso sarà 1 – p. Si ripete n volte la prova in condizioni identiche e indipendenti tra di loro: nel nostro caso, come è avvenuto quando si cercava il colpevole nel capitolo 14 di Samuele, si divide l'esercito in due gruppi, si gettano le sorti, il gruppo che sortisce Urim viene ulteriormente diviso in due, e così via. Si dice distribuzione di Bernoulli, o distribuzione binomiale, quella che conta il numero complessivo k di successi sulle n prove; essa prende il nome dal suo ideatore, il matematico svizzero Jakob Bernoulli (1654-1705). Si può dimostrare che la distribuzione binomiale è espressa dalla formula:
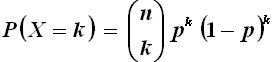
con k = 0, 1, 2, ..., n. Di solito la si indica con B(n,p). Si può anche dimostrare che:
E(X) = n p ; V(X) = n p (1 – p)
Siano ad esempio cinque casi di innocenza o colpevolezza da giudicare per mezzo degli Urim e Tummim. Qual è la probabilità di avere esattamente tre giudizi di innocenza? Gli esiti sono solo due, Urim o Tummim, Tummim rappresenta il successo, e la sua probabilità è 1/2; io devo sortirne k = 3. Si ha così:
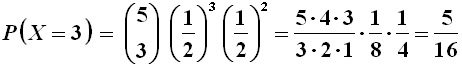
cioè il 31 %. Si ha poi E(X) = 5 x 1/2 = 2,5 e V(X) = 5 x 1/2 x (1 – 1/2) = 1,25.
Un'altra importante distribuzione discreta di probabilità è la distribuzione di Poisson, che si può ricavare come approssimazione di quella binomiale. Essa trae il suo nome dal matematico francese Siméon-Denis Poisson (1781-1840). Una variabile aleatoria è detta di Poisson (o poissoniana) con parametro λ > 0 se la sua distribuzione di probabilità è data da:
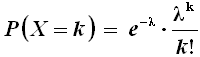
con k = 0, 1, 2, ... Di solito la si indica con P(λ). Essa approssima tanto meglio il comportamento della variabile aleatoria quanto più n è grande e p è piccola. Di solito la si usa quando della variabile aleatoria si conosce il valore medio ma non i valori esatti di n e di p, perchè:
E(X) = λ ; V(X) = λ
Essa è importantissima in Fisica, perchè si presenta in un gran numero di situazioni. Ad esempio, il numero di particelle alfa emesse da una radiosorgente in un tempo fisso è una variabile aleatoria poissoniana. Si prenda in considerazione il Re Davide, del quale ben sappiamo cosa dovette fare per conquistare la mano di Mical, figlia di Saul:
« Allora Saul disse: "Riferite a Davide: Il re non vuole il prezzo nuziale, ma solo cento prepuzi di Filistei, perché sia fatta vendetta dei nemici del re." Saul tramava di far cadere Davide in mano ai Filistei. » (1 Sam 18, 25)
Supponiamo dunque che, in media, un eroe come Davide abbatta 100 Filistei in un solo giorno. Qual è la probabilità che ne abbatta 120? X è il numero di nemici uccisi, ma non conosciamo la probabilità esatta che un Filisteo venga ammazzato. Siccome però λ = 100, ipotizzando una distribuzione di Poisson avremo:
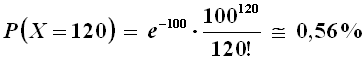
Il calcolo sopra riportato non può essere eseguito con normali calcolatrici tascabili, dato che il risultato di 120! è fuori dalla loro portata, ma io vi sono arrivato usando la cosiddetta formula di Stirling:
![]()
valida per n molto grandi. Nel nostro caso, sostituendo nella precedente si ha:
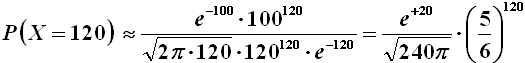
Questo calcolo si può effettuare anche con una semplice calcolatrice tascabile e fornisce 0,0056, cioè proprio lo 0,56 % sopra determinato. E se questa probabilità vi pare piccola, ricordatevi che Davide portò a Saul i prepuzi di ben 200 nemici uccisi in battaglia (« Non erano ancora compiuti i giorni fissati, quando Davide si alzò, partì con i suoi uomini e abbatté tra i Filistei duecento uomini » 1 Sam 18, 26-27). Se provate a calcolare P(X = 200) con la formula sopra riportata, troverete 5 x 10–19, cioè una probabilità praticamente pari a zero! Eppure Davide ce l'ha fatta...
Vi sono però molti fenomeni naturali per descrivere i quali le variabili discrete non sono adatte, ed occorrono invece delle variabili aleatorie continue, che possono cioè assumere tutti i valori reali all'interno di un certo intervallo. Tali variabili ad esempio sono necessarie per descrivere la durata della vita di un individuo o di una particella subatomica, la distanza percorsa da un cammello nel deserto prima di sentire la necessità di bere o il cammino libero medio percorso da una particella. Anche la misura di grandezze fisiche è soggetta ad errore, e quindi è da considerare una variabile aleatoria continua.
In questo caso non ci si chiede qual è la probabilità che la variabile assuma esattamente un dato valore, ma piuttosto che la variabile assuma valori all'interno di un dato intervallo. Dire ad esempio che la misura di una lunghezza è pari a 10 centimetri con un errore dell'1 % significa dire che quella lunghezza è compresa tra 9,9 e 10,1 centimetri. Nel caso di variabili aleatorie continue non si parla di distribuzioni di probabilità, ma di densità di probabilità. Essa è una funzione f(x) positiva o nulla per ogni valore di x e normalizzata, tale cioè che:
![]()
Allora la probabilità che la X assuma valori compresi in un certo intervallo [ a ; b ] è data da:
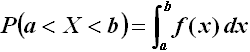
Ne consegue che la probabilità cercata è l'area sottesa dal grafico della densità di probabilità nell'intervallo [ a ; b ]. Si noti che la probabilità che X assuma esattamente un certo valore a è pari a zero. È diversa da zero solo la probabilità che X sia compresa dentro un determinato intervallo, come si evince dal seguente grafico:
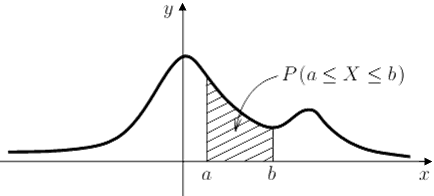
Data una variabile aleatoria continua X di densità f(x), il suo valore medio o valore atteso è dato da:

La sua varianza è invece così definita:
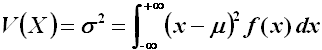
Però è più semplice calcolarla tramite questa formula:
![]()
Si dice invece funzione di ripartizione di una variabile continua X di densità f(x) la funzione così definita:
![]()
E si ha F '(x) = f(x). In particolare si dice che una variabile casuale continua ha una distribuzione uniforme sull'intervallo [ a ; b ] se la sua densità di probabilità è costante tra a e b, e vale zero al di fuori di tale intervallo. In pratica, l'area sottesa dal grafico è quella di un rettangolo, che vediamo qui sotto colorato di giallo:

La funzione deve essere normalizzata, per cui l'area di tale rettangolo deve essere pari ad 1. Dato che la base misura ( b – a ), l'altezza misura 1/( b – a ). La sua densità di probabilità perciò è data da:
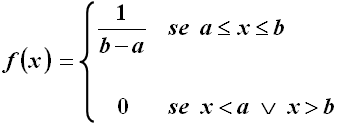
Usando le formule sopra scritte, si ricava che:
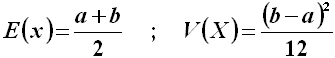

Caifa, con tanto di pettorale con
le dodici pietre, interpretato
da Bob Bingham nel musical "Jesus Christ Superstar" (1973)
Facciamo un esempio in tema con questo nostro ipertesto. Nel Tempio di Gerusalemme si tiene il primo ufficio liturgico alle 6.15 del mattino e poi uno ogni 15 minuti. Ogni giorno un pio Ebreo si reca al Tempio di Gerusalemme in un orario compreso tra le 6.00 e le 6.30, e segue il primo ufficio liturgico che comincia. Qual è la probabilità che debba aspettare l'inizio della liturgia più di 5 minuti? In pratica, il pio Ebreo arriva in un orario che si può assimilare alla scelta di un numero a caso nell'intervallo [ 0 ; 30 ], scelta indicata con la variabile casuale X con distribuzione uniforme. Deve attendere più di 5 minuti solo se arriva tra le 6.00 e le 6.10 o tra le 6.15 e le 6.25, dunque la probabilità cercata è P = P(0 < X < 10) + p (15 < x < 25), ovvero:
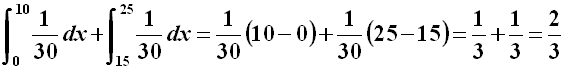
cioè il 67 %. Ma la distribuzione uniforme non è la più usuale, in natura; anzi, è piuttosto raro imbattersi in essa. In genere piuttosto si ha a che fare con la distribuzione gaussiana, il cui nome è un omaggio a quello di Carl Friedrich Gauss (1777-1855), detto "il Principe dei Matematici". Questa distribuzione è detta anche normale, proprio per la normalità con cui la si ritrova in natura. Gauss la descrisse per la prima volta nel 1809 studiando il moto dei corpi celesti, ma ben presto si accorse che essa compariva in una grande varietà di fenomeni molto diversi, dagli errori nelle misure alle vittorie nel gioco d'azzardo, fino alla distribuzione dei tiri attorno ai bersagli. Bisogna però dire che proprio nel 1809 il matematico statunitense Robert Adrain (1775-1843) pubblicò uno studio sulla distribuzione normale, simultaneamente ed indipendentemente da Gauss, anche se i suoi lavori rimasero gnorati dalla comunità scientifica fino al 1871. Alcuni autori poi ritengono che il francese Abraham de Moivre (1667-1754) abbia già scoperto tale distribuzione fin dal 1738. Nel 1835 il belga Lambert Adolphe Quetelet (1796-1874) dimostrò che i dati riguardanti la misura del torace di soldati scozzesi e la statura dei militari di leva francesi obbedivano alla distribuzione gaussiana, e la sua importanza venne consacrata nell'olimpo della matematica.
La distribuzione gaussiana, indicata con N(μ,σ), è definita come la distribuzione che ha densità di probabilità espressa dalla funzione:
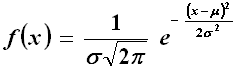
dove E(X) = μ e V(X) = σ2. Il grafico di tale funzione è definita positiva, è simmetrica rispetto alla retta x = μ, presenta un massimo proprio in x = μ, ha l'asse x come asintoto orizzontale e due flessi nei punti x = μ ± σ:
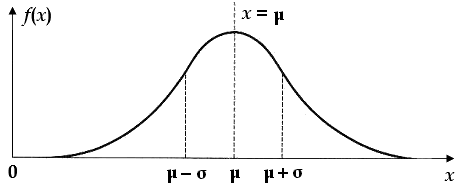
Essa è comunemente conosciuta con il nome di "campana di Gauss". Se in particolare μ = 0 e σ = 1, si parla di distribuzione gaussiana standard. Di solito, per calcolare la probabilità in una distribuzione di tipo gaussiano, si passa attraverso la distribuzione standardizzata, che per distinguerla da quella generica è scritta con la variabile z:
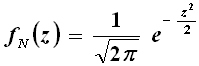
A sua volta, il calcolo della probabilità di una variabile casuale gaussiana standard passa attraverso la sua funzione di ripartizione, indicata di solito con la lettera greca Φ:
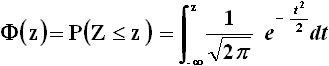
Questo integrale non può essere risolto alle quadrature, cioè con uno dei procedimenti tradizionali (per sostituzione, per parti, ecc.), ma solo per via numerica, ed esistono tabelle che ne forniscono i valori con parecchie cifre decimali; noi useremo quella con cinque cifre decimali che potete visualizzare cliccando qui. Di solito in esse sono contenuti i soli valori positivi di z; i valori negativi si ricavano sfruttando la simmetria della gaussiana standard rispetto all'asse y. In generale, bisogna ricordare che:
P(Z < – z) = Φ(– z) = 1 – Φ(z) = 1 – P(Z < z)
Facciamone alcuni esempi:
P(Z < 1) = Φ(1) = 0,84134 = 84,134 %
P(0 < Z < 1) = P(Z < 2) – P(Z < 1) = Φ(2) – Φ(1) = 0,97725 – 0,5 = 0,47725 = 47, 725 %
P(Z > 1) = 1 – P(Z < 1) = 1 – Φ(1) = 1 – 0,84134 = 0,15866 = 15,866 %
P(Z < – 2) = P(Z > 2) = 1 – P(Z < 2) = 1 – Φ(2) = 1 – 0,97725 = 0,02275 = 2,275 %
P(Z > – 1) = P(Z < 1) = Φ(1) = 0,84134 = 84,134 %
P(– 1,5 < Z < – 0,5) = P(0,5 < Z < 1,5) = Φ(1,5) – Φ(0,5) =
= 0,93319 – 0,69146 = 0,24173 = 24, 173 %
E se la distribuzione non è standardizzata? Data una distribuzione normale qualsiasi N(μ,σ), si può dimostrare che la variabile casuale così definita:
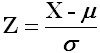
è sicuramente standard. Ne consegue che:
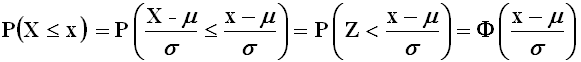
Proviamo a calcolare la probabilità che X cada nell'intervallo [ μ – σ ; μ + σ ]. Si ha:
P( μ – σ < X < μ + σ ) = P(X < μ + σ) – P(X < μ – σ) =
= Φ [(μ + σ – μ)/σ] – Φ [(μ – σ – μ)/ σ] = Φ(1) – Φ(– 1) =
= Φ(1) – [ 1 – Φ(1) ] = 2 Φ(1) – 1 = 2 x 0,86433 – 1 = 0,68268
Dunque vi è il 68,3 % di probabilità che i valori cadano in questo intervallo. Con calcoli assolutamente analoghi, che vi invito a provare ad eseguire come esercizio, si dimostra che vi è il 95,4 % di probabilità che X cada tra μ – 2 σ e μ + 2 σ, e il 99,7 % di probabilità che cada tra μ – 3 σ e μ + 3 σ. Ne consegue che quasi tutta l'area sottesa dalla gaussiana è compresa nell'intervallo [ μ – 3 σ ; μ + 3 σ ], poiché solo lo 0,27 % è al di fuori di esso. Per questo le tavole dei valori di Φ(z) non riportano mai valori oltre il 3 o il 4.
Le variabili casuali normali descrivono un gran numero di fenomeni, in cui la maggior parte dei valori di X sono addensati intorno ad un valor medio μ. Ne sono tipici esempi l'effettiva lunghezza di un oggetto prodotto da una macchina a controllo numerico (in tal caso, μ è il valore impostato su di essa), la distribuzione della statura, del peso, del consumo calorico giornaliero ecc. di una certa popolazione, i risultati di un test universitario o di un concorso, e così via. Facciamo ora un esempio in sintonia con il nostro ipertesto. Un fornaio di Gerusalemme produce pani da offrire al Tempio, che possono essere mangiati solo dai Sacerdoti, con l'eccezione del Re Davide, come ricorda un noto passo evangelico:
« Ciò vedendo, i farisei gli dissero: "Ecco, i tuoi discepoli stanno facendo quello che non è lecito fare in giorno di sabato." Ed egli rispose: "Non avete letto quello che fece Davide quando ebbe fame insieme ai suoi compagni? Come entrò nella casa di Dio e mangiarono i pani dell'offerta, che non era lecito mangiare né a lui né ai suoi compagni, ma solo ai sacerdoti?" » (Matteo 12, 2-4)
I pani prodotti da quel fornaio dovrebbero pesare tutti 500 grammi. In base all'analisi statistica su campioni presi a caso, però, si stima che il peso effettivo delle pagnotte prodotte possa essere trattato come una variabile casuale normale, con media μ = 500 e varianza σ2 = 36. Le pagnotte vengono consegnate al Tempio solo se il loro peso di discosta meno del 5 % dal valore medio. Quante ne saranno scartate?
Il 5 % di 500 grammi equivale a 25 grammi, quindi per risolvere il problema devo determinare la probabilità che le pagnotte abbiano peso compreso tra 500 – 25 = 475 e 500 + 25 = 525 grammi. Standardizziamo la variabile: a X = 475 corrisponde il nuovo valore Z = (475 – 500)/36 = – 0,69, e a X = 525 corrisponde il nuovo valore Z = (525 – 500)/36 = + 0,69. La probabilità cercata è allora pari a:
P(X < 475 \/ X > 525) =P (Z < – 0,69 \/ Z > + 0,69) =
= P(Z > + 0,69) + P(Z > + 0,69) = 2 [ 1 – Φ(0,69)] = 0,49018 = 49 %
Ne dovremo dunque scartare circa il 49 %.
Prima di passare ad una nuova lezione, vorrei illustrare un altro esempio riguardante la distribuzione normale, tratto non dalla Bibbia ma da dal famoso romanzo "Jurassic Park" di Michael Crichton (1942-2008). In esso, e precisamente nella "Terza Iterazione" (terza parte), l'ingegnere informatico John Arnold mostra agli altri personaggi del libro un grafico, generato dal suo computer, che illustra la distribuzione dei dinosauri del genere Procompsognathus ricreati nel parco, cioè il loro numero (in ordinate) in funzione della loro altezza in centimetri (in ascisse):
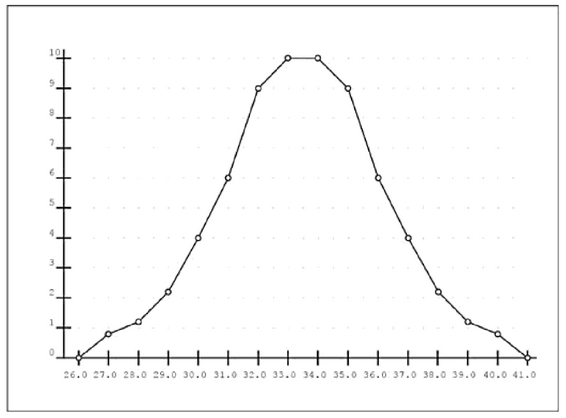
Il matematico Ian Malcolm però obietta che tale distribuzione non è realistica, proprio perchè è "normale". Infatti il genetista Henry Wu ha spiegato che i "compy" (come vengono chiamati nello slang americano) sono stati introdotti nel parco in tre gruppi, ad intervalli di sei mesi l'uno dall'altro; e siccome tali gruppi sono stati geneticamente creati indipendentemente l'uno dall'altro, ciò che si dovrebbe vedere sarebbero tre distribuzioni gaussiane diverse, sovrapposte tra di loro:
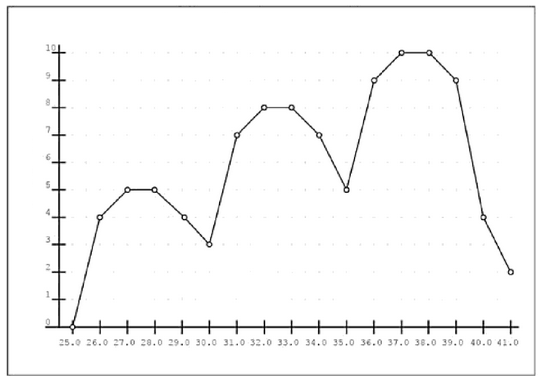
La distribuzione gaussiana singola che si vede sul computer, conclude Malcolm, è quella di una popolazione che si sta riproducendo. « Non vedo come », ribatte seccamente Henry Wu, dato che tutti i dinosauri del Jurassic Park sono femmine. La risposta viene fornita più avanti nel romanzo: il DNA dei dinosauri, incompleto a causa dei milioni di anni trascorsi dalla sua fossilizzazione, è stato completato da Wu con del DNA di rospo; e i rospi sono in grado, in presenza di una popolazione di soli maschi o di sole femmine, di cambiare sesso, così da permettere la conservazione della specie. Ed è puntualmente quanto è successo ad Isla Nublar. Appare quasi incredibile che Ian Malcolm possa essersene accorto solo osservando una distribuzione aleatoria, ma questo non fa altro che dimostrare la potenza e l'importanza della statistica e delle distribuzioni discrete e continue di probabilità!
![]()