Più con un gigante io mi convegno

Lo 'mperador del doloroso regno
da mezzo 'l petto uscia fuor de la ghiaccia;
e più con un gigante io mi convegno,
che i giganti non fan con le sue braccia...

(Inf. XXXIV, 28-31)

L'aritmetica (dal greco "αριθμός", "numero"), è la branca più antica della matematica, e studia le proprietà elementari delle operazioni sui numeri. Nel "Convivio", Dante la chiama "arismetrica", termine mai attestato al di fuori di quest'opera dantesca. Nel paragonare i sette cieli del Paradiso alle sette arti del Trivio e del Quadrivio, Dante scrive in particolare:

« E lo cielo del Sole si può comparare a l'Arismetrica per due proprietadi: l'una si è che del suo lume tutte l'altre stelle s'informano; l'altra si è che l'occhio nol può mirare. E queste due proprietadi sono ne l'Arismetrica: ché del suo lume tutte s'illuminano le scienze, però che li loro subietti sono tutti sotto alcuno numero considerati, e ne le considerazioni di quelli sempre con numero si procede [...] L'altra proprietade del Sole ancor si vede nel numero, del quale è l'Arismetrica: che l'occhio de lo 'ntelletto nol può mirare; però che 'l numero, quant'è in sé considerato, è infinito, e questo non potemo noi intendere (Convivio II, XIII, §§15-16, 19)

La definizione di aritmetrica (o Arismetrica) come scienza dei numeri, ai tempi di Dante era definizione comune: « Arithmetica est scientia numerorum... inter disciplinas mathematicas ideo primam esse... quoniam ipsa ut sit nullam aliam indiget disciplinam. » (Isidoro di Siviglia, Etimologie III, I, 1). Non si sa chi per primo si occupò di aritmetica, ma certamente egli visse nella più remota preistoria, e fece ricorso ai numeri interi (uno, due, tre...) pratici. come contare i capi di selvaggina abbattuti durante una battuta di caccia. La più antica testimonianza di attività aritmetica è unanimemente considerato il cosiddetto osso di Ishango, il perone di un babbuino rinvenuto vicino al confine tra l'Uganda e il Congo, e datato tra il 20.000 e il 18.000 a.C. (cioè al Paleolitico Superiore). Esso è ricoperto da una serie di scalfitture raggruppate in tre colonne che occupano tutta la lunghezza dell'oggetto. I numeri di tacche sulle colonne sono raggruppati in insiemi ben precisi: quelli della prima colonna sono tutti dispari (9, 11, 13, 17, 19 e 21); quelli incisi nella colonna di sinistra sono tutti numeri primi compresi tra 10 e 20, quelli sulla colonna centrale sono raggruppati in coppie in cui un elemento è doppio dell'altro, quelli della colonna di destra sono così interpretabili: 10 + 1, 10 – 1, 20 + 1 e 20 – 1 Alcuni studiosi sostengono che l'osso possa essere un calendario lunare di sei mesi, in relazione al ciclo mestruale femminile. Naturalmente non tutti concordano con questa interpretazione (le tacche potrebbero avere uno scopo puramente decorativo), ma tra gli esperti vi è generale accordo circa il fatto che gli assiro-babilonesi conoscessero quasi tutti gli aspetti dell'aritmetica elementare già intorno al 2000 a.C., avendoli sviluppati per scopi astronomici e divinatori, come dimostra la tavoletta d'argilla Plimpton 322, che contiene una lista di terne pitagoriche. Pitagora di Samo (575-495 a.C.) suppose che tutto l'universo fosse costruito sulla base di numeri razionali, cioè di rapporti tra numeri interi; paradossalmente però proprio il teorema di Pitagora portò a scoprire l'esistenza dei numeri irrazionali, numeri decimali che non possono essere scritti sotto forma di frazione. Ad esempio, un triangolo rettangolo isoscele i cui cateti misurano 1 ha l'ipotenusa che misura radice di 2, un numero manifestamente irrazionale. Inizialmente i pitagorici (che costituivano una setta chiusa ed iniziatica) tentarono di tenere segreta la scoperta; secondo la leggenda, il pitagorico Ippaso di Metaponto sarebbe stato punito dagli dei morendo in un naufragio proprio per aver rivelato al mondo l'esistenza dei numeri irrazionali, che "rovinavano" l'ingenua rappresentazione razionale del mondo predicata dal suo maestro.

Anche i più semplici calcoli aritmetici rappresentavano però un'impresa ardua da effettuarsi con la notazione di Greci e Romani. Tutto divenne più facile con l'introduzione della notazione posizionale e delle dieci cifre (compreso lo zero) da parte dei matematici indiani Brahmagupta (598–668) ed Aryabhata (476-550). Già nel VII secolo il vescovo siriaco Severo Sebokht menzionava questo metodo lodandone la praticità, ma furono gli Arabi a diffonderne l'uso in tutto il Mediterraneo (da cui il termine "cifre arabe"). L'introduzione di tale metodo di calcolo in Europa avvenne grazie a Gerbert d'Aurillac (950-1003), uomo dottissimo che nel 999 divenne Papa con il nome di Silvestro II, e di Leonardo Fibonacci di Pisa (1170-1249) nel suo fondamentale "Liber Abaci". Alla fioritura della Matematica nel mondo islamico medievale e nell'Europa Rinascimentale ha certamente contribuito l'enorme semplificazione dei calcoli aritmetici consentita dalla notazione posizionale.

Che Dante fosse ancora in larga parte legato alla vecchia numerazione romana, basata su una notazione additiva o sottrattiva, ce lo dice il seguente passo del Purgatorio:

« Io veggio certamente, e però il narro,
a darne tempo già stelle propinque,
secure d'ogn' intoppo e d'ogne sbarro,
nel quale un cinquecento diece e cinque,
messo di Dio, anciderà la fuia
con quel gigante che con lei delinque » (Purg. XXXIII, 40-45)

Con questi versi Beatrice vuole dire: io vedo per certo che stanno per sorgere delle costellazioni, libere da ogni contrasto e da ogni impedimento umano, le quali annunceranno il sorgere di un messo celeste, il quale ucciderà la prostituta ("fuia", letteralmente "ladra") e il gigante scorti poco prima da Dante, simboli rispettivamente della Chiesa corrotta e del Re di Francia, traditori della vera Chiesa di Cristo e dell'Impero. Questo inviato del cielo è indicato con un nome enigmatico: cinquecentoquindici. Esso richiama una nota citazione dell'Apocalisse, che ho esaminato in un altro ipertesto:

« Qui sta la sapienza. Chi ha intelligenza calcoli il numero della bestia: essa rappresenta un nome d'uomo. E tale cifra è seicentosessantasei. » (13, 18)

Quasi tutti i commentatori leggono in questo numero la parola DVX, perchè cinquecento nella numerazione latina si scrive D, dieci di scrive X (due mani aperte) e cinque si scrive V (una mano aperta). Altri leggono invece le lettere latine senza bisogno di anagramma come iniziali di "Domini Xristi Vertagus", con riferimento alla celebre profezia del veltro di Inf. I, 101. È possibile che Dante pensasse all'imperatore Enrico VII di Lussemburgo, oppure a Cangrande della Scala, vicario imperiale nel 1318. In ogni caso, appare chiaro il riferimento alla classica numerazione latina, anziché a quella araba posizionale.

Com'è intuitivo, i primi numeri ad essere ideati ed utilizzati furono i numeri naturali (così detti perchè scaturiscono in modo naturale dal conteggio si diversi oggetti), cioè gli interi senza segno, e Dante è consapevole della loro importanza quando li utilizza addirittura per riferirsi alla Santissima Trinità:

« Quell' uno e due e tre che sempre vive
e regna sempre in tre e 'n due e 'n uno,
non circunscritto, e tutto circunscrive » (Par. XIV, 28-30)

Come commenta Manfredi Porena, Dio è Colui che vive e regna sempre essendo una Sostanza (la Divinità), due Nature (l'umana e la divina nella persona di Cristo) e tre Persone: Padre, Figlio e Spirito Santo. Tecnicamente questa figura retorica prende il nome di chiasmo (dalla lettera greca Chi, che ha la forma di una X), giacché i termini del primo verso si ritrovano scambiati tra di loro nel secondo, e il Sapegno aggiunge: « il movimento melodico di questi versi, dove i vocaboli ad uno ad uno, quasi note staccate, si riecheggiano in ordine inverso », crescente prima e decrescente poi, « danno l'impressione, quasi si direbbe la presenza sensibile, di una pienezza di perfezione che in se stessa si esaurisce e su se stessa ritorna come un circolo ». Non può non venire in mente questo passo del Convivio:

« Non solamente in tutti insieme, ma ancora in ciascuno è numero, chi ben considera sottilmente; per che Pittagora, secondo che dice Aristotile nel primo de la Fisica, poneva li principii de le cose naturali lo pari e lo dispari, considerando tutte le cose esser numero. » (Convivio II, XIII, 18)

Naturalmente, dalla preistoria fino ad oggi il concetto di numero ha subito parecchi ampliamenti. Oggi si conoscono cinque insiemi numerici, contenuti l'uno nell'altro. L'insieme N è quello dei numeri naturali (interi senza segno), introdotti per meri fini pratici. Siccome la somma tra numeri naturali è sempre possibile ma la sottrazione no (l'operazione 3 – 4 non ha alcun risultato in N) venne introdotto l'insieme Z dei numeri relativi, interi con segno. La moltiplicazione è sempre possibile in Z, ma la divisione no (5 : 7 non ha alcun risultato in Z), e così venne introdotto l'insieme Q dei numeri razionali, cioè delle frazioni. La potenza di una frazione è sempre un'altra frazione, ma la radice no: ad esempio la radice quadrata di 3/4 non esiste in Q. Per questo fu introdotto l'insieme R dei numeri reali, i quali comprendono anche i suddetti numeri irrazionali. Infine, per rendere possibile estrarre le radici quadrate di numeri negativi (nessun numero reale ha quadrato – 3), venne introdotto l'insieme C dei numeri complessi. I naturali sono particolari relativi (2 si può scrivere + 2), i relativi sono particolari razionali ( – 4 equivale a – 4/1), i razionali sono particolari numeri reali, e i reali sono particolari numeri complessi con parte immaginaria nulla, per cui ogni insieme è contenuto dentro il successivo (per ricordare l'ordine esatto di questi insiemi si ricorre alla filastrocca inglese "Nine Zulu Queens Ruled Congo"):

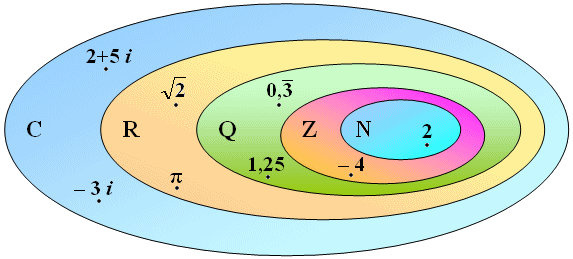
In realtà gli insiemi non furono introdotti in quest'ordine, ma nel seguente: N, Q, R, Z, C. I numeri interi erano noti già nella Preistoria; Assiro-Babilonesi ed egizi introdussero le frazioni; la scuola pitagorica scopì l'esistenza dei numeri irrazionali verso il 600 a.C.; i numeri negativi, contrariamente a quanto si crede di solito, comparvero piuttosto tardi, nel Rinascimento; i numeri complessi debuttarono nel XVII secolo. La descrizione precedente tuttavia rende ragione del fatto che ogni insieme numerico è contenuto in uno più vasto, esattamente come aumentano le necessità del calcolo man mano che la Matematica prosegue nel suo sviluppo.

Ma Dante va ben al di là di una semplice constatazione dell'esistenza dei numeri interi, come potrebbe parere ad una prima lettura. Prendiamo infatti in considerazione questi versi del Purgatorio:

« Tu credi che a me tuo pensier mei
da quel ch'è primo, così come raia
da l'un, se si conosce, il cinque e 'l sei » (Par. XV, 55-57)

In essi Cacciaguida afferma che il suo discendente crede che il suo pensiero discenda ("mei") nella sua anima direttamente da Dio ("quel ch'è primo"), così come dalla conoscenza dell'unità deriva ("raia", cioè si irraggia) quella di tutti gli altri numeri, come ad esempio il 5 e il 6. L'avo di Dante prosegue poi aggiungendo che questa convinzione risponde al vero, poiché tutti i beati, qualunque sia il grado della loro beatitudine, contemplano Dio nel quale, come in uno specchio, ogni pensiero umano si riflette prima ancora che venga pensato. In questa similitudine, che di per sé sembra riflettere solo una proprietà piuttosto ovvia dei numeri naturali, è in realtà possibile ravvisare una prima anticipazione degli Assiomi di Peano.

Il matematico cuneese Giuseppe Peano (1858-1932) formulò infatti cinque assiomi in base ai quali è possibile definire i numeri naturali, e tutta l'aritmetica, prescindendo da qualunque intuizione legata a necessità contingenti (il conteggio dei giorni, dei capi di bestiame, ecc.). Partendo dai tre concetti primitivi di numero, uno e successivo, essi sono i seguenti:

Il primo assioma ci dice che l'insieme non è vuoto, contenendo almeno un elemento, l'uno. Il secondo istituisce una relazione S (la relazione Successivo) che si applica agli elementi dell'intero insieme. Il terzo assioma ci permette di escludere sistemi numerici in cui partendo da uno e andando avanti da un elemento al successivo si possa ritornare su un elemento già visitato ed entrare in un ciclo chiuso. Il quarto afferma che nessun numero ha come successivo uno, e ciò leva di mezzo sistemi di numerazione in cui si entra in un ciclo che torna al punto di partenza. Di conseguenza, terzo e quarto assioma escludono qualsiasi sistema numerico dotato di un numero finito di elementi.

Il quinto assioma di Peano è noto anche come Principio di Induzione, ed è oggi molto usato in Matematica. Esso afferma che l'insieme N dei numeri naturali è il più piccolo insieme che contiene l'uno e il successivo di ogni suo elemento. Questo assioma ci permette di escludere sistemi numerici in cui siano presenti altri elementi estranei alla sequenza infinita dei successori dell'uno.

Da notare che un concetto molto simile a questo era trovato da Dante nell'"Ars Geometrica" di Severino Boezio, in cui si affermava:

« Primus autem numerus est binarius; unitas enim...numerus non est, sed fons et origo numerorum »
[Il primo numero è il due, infatti l'unità non è un numero, ma l'inizio e l'origine dei numeri]

Si potrebbe pensare che, dopo Peano, l'aritmetica sia ormai una porzione della Matematica che non può riservare altre sorprese, essendo basato sullo studio elementare dei numeri; invece non è così. Dall'aritmetica è infatti nata la Teoria dei Numeri, avviata dal francese Pierre de Fermat (1601-1665), che sfrutta i meccanismi del calcolo infinitesimale e dell'analisi complessa per affrontare problemi relativi ai numeri interi. Essa solitamente affronta questioni esprimibili attraverso concetti comprensibili anche a chi non è matematico di professione, ma che hanno resistito anni, se non secoli, prima di venire risolte, o che restano tuttora prive di soluzione. Tra i numerosissimi problemi aperti di questa disciplina vi sono la Congettura di Goldbach (ogni numero pari maggiore di 2 è esprimibile come somma di due numeri primi), avanzata nel 1742; la Congettura di Polignac (per ogni numero intero positivo N esistono infiniti numeri primi consecutivi la cui differenza è pari a 2N), proposta nel 1849; e la Congettura di Euclide sui Primi Gemelli (esistono infinite coppie di numeri primi che differiscono di due), che resiste ad ogni dimostrazione addirittura da 2300 anni. La Teoria dei Numeri è una disciplina difficilissima: essa comprende argomenti estremamente distanti dal significato normale che noi diamo alla parola "aritmetica", come le forme modulari, la legge di reciprocità quadratica, i campi p-adici, gli operatori di Hecke, la Funzione Zeta di Riemann, e chi più ne ha, più ne metta.

Pochi conoscono le due lezioni che lo scienziato pisano Galileo Galilei (1568-1642) tenne sulla struttura dell'Inferno dantesco. Nel 1588 il giovane Galileo (all'epoca aveva solo 24 anni) fu chiamato dall'Accademia Fiorentina a tenere alcune conferenze di argomento letterario su Dante, Ariosto e Tasso. Se per gli ultimi due Galileo si limitò ad una valutazione letteraria della loro opera, molto più interessanti sono le due lezioni che il futuro fondatore della scienza moderna tenne "circa la figura, sito e grandezza dell'Inferno di Dante". In esse infatti lo scienziato pisano sostiene che il "Ghibellin fuggiasco" disseminò la sua opera poetica di riferimenti geometrici e matematici, sufficienti per ricostruire con precisione l'estensione e la geometria dell'imbuto infernale.

In questa sede, dedicata all'aritmetica dantesca, analizzeremo nei dettagli una delle sezioni più interessanti dei calcoli svolti da Galileo, e precisamente quelli riguardanti il Cocito (in greco "pianto"), cioè il lago ghiacciato che occupa il punto più profondo dell'inferno:

« Per ch'io mi volsi, e vidimi davante
e sotto i piedi un lago che per gelo
avea di vetro e non d'acqua sembiante » (Inf. XXXII, 22-24)

Esso è diviso in quattro zone: la Caina, dove vengono puniti i traditori dei parenti, seppelliti nel ghiaccio fino al collo (dal nome del biblico Caino); l'Antenora, dove sono puniti i traditori della patria, sepolti fino alla cintola, con la parte superiore del corpo esposta ai gelidi venti infernali (dall'eroe omerico Antenore, che avrebbe tradito la sua patria, Troia); la Tolomea, dove soggiornano i traditori degli ospiti, distesi supini con la parte posteriore del corpo immersa nel ghiaccio (da Tolomeo, che fece uccidere Pompeo Magno credendo di fare un favore a Cesare); e la Giudecca, dove si trovano coloro che tradirono i benefattori dell'umanità, completamente immersi nel ghiaccio (dal nome di Giuda Iscariota). Nel bel mezzo dell'ultima zona fa orribile mostra di sé il signore dell'Inferno, Lucifero:

« Lo 'mperador del doloroso regno
da mezzo 'l petto uscia fuor de la ghiaccia... » (Inf. XXXIV, 28-29)

Galileo sostiene che, leggendo con attenzione questi versi, è possibile dedurre l'estensione delle zone del Cocito. Dante infatti aggiunge, parlando del sovrano dell'Inferno:

« ...e più con un gigante io mi convegno,
che i giganti non fan con le sue braccia:
vedi oggimai quant'esser dee quel tutto,
ch'a così fatta parte si confaccia! » (Inf. XXXIV. 28-33)

Seguiamo il ragionamento di Galileo. L'Alighieri ci dice che la « ghiaccia », cioè lo strato di ghiaccio in cui sono confitti per intero i peccatori della Giudecca, arriva a metà del petto di Lucifero. Ma alcuni versi più sotto Dante ci dice chiaramente che l'ombelico di Lucifero coincide con il centro della Terra, « il punto al qual si traggon d'ogne parte i pesi »:

« Quando noi fummo là dove la coscia
si volge, a punto in sul grosso de l'anche,
lo duca, con fatica e con angoscia,
volse la testa ov'elli avea le zanche,
e aggrappossi al pel com'om che sale,
sì che 'n inferno i' credea tornar anche. » (Inf. XXXIV, 76-81)

« Di là fosti cotanto quant'io scesi;
quand'io mi volsi, tu passasti 'l punto
al qual si traggon d'ogne parte i pesi. » (Inf. XXXIV, 109-111)

Se ne deduce che la distanza che intercorre tra l'ombelico e la metà del petto di Lucifero corrisponde esattamente al raggio della superficie ghiacciata della Giudecca. Che quest'ultima abbia forma sferica e non quella piatta tipica di un lago ghiacciato, come si è visto nella rappresentazione di Doré sopra riportata, lo conferma a Dante lo stesso Virgilio:

« Tu hai i piedi in su picciola spera,
Che l'altra faccia fa della Giudecca » (Inf. XXXIV, 116-117)

ma ce lo dice anche la logica, visto che il centro della Terra è molto vicino, e si potrebbe camminare agevolmente solo su di una superficie di tale forma. In realtà, è facile dimostrare mediante la meccanica newtoniana che a quella profondità la gravità sarebbe pressoché nulla, come vedremo in una delle prossime lezioni, ma di questo ora non terremo conto come se fosse una licenza poetica, poiché Dante e Virgilio non avrebbero certo potuto raggiungere il pertugio necessario per portarsi nel Purgatorio, in assenza di peso.

Ora, ai tempi di Galileo erano note molte proporzioni che regolavano le distanze tra le parti del corpo, studiate con cura ad esempio da Leonardo da Vinci nel suo celeberrimo "uomo vitruviano". Pertanto il problema della misura può essere ridotto a questo interrogativo: quanto è alto Lucifero?

Anche in questo caso i versi ci vengono in aiuto. La terzina con cui abbiamo aperto questa pagina può essere infatti considerata la riscrittura in termini poetici di una normale proporzione, del tipo:

Dire infatti « più con un GIGANTE IO mi convegno / che i GIGANTI non fan con le SUE BRACCIA » significa dire che nella proporzione suddetta:

altezza di Dante : altezza dei Giganti = altezza dei Giganti : braccio di Lucifero

Insomma, il Gigante è medio proporzionale tra Dante e Belzebù. In realtà Dante con i termini « PIÙ CHE » lascia intendere che il rapporto tra un braccio di Lucifero e la dimensione dei Giganti del XXXI Canto è assai maggiore di quello tra l'altezza di Efialte o di Nembrotte e quella di Dante; perciò la nostra proporzione ci darà solo il limite inferiore dell'altezza della « creatura ch'ebbe il bel sembiante » (Inf. XXXIV, 18). Per i fini che ci interessano, comunque, un limite inferiore alle dimensioni della Giudecca è assai meglio che niente.

Ora, nelle biografie di Dante si parla di un uomo di media statura, pertanto facilmente stimabile in tre braccia dell'epoca. Il braccio fiorentino corrisponde a 0,583 metri, per cui Dante era alto circa un metro e settantacinque. Più difficile è risalire all'altezza di uno dei Giganti immaginati dall'Alighieri, ma Galileo non si dà per vinto, convinto che non esiste problema di stima per cui Dante non ci abbia lasciato qualche indizio. Torniamo infatti al Canto XXXI dell'Inferno, quello degli « orribili giganti, cui minaccia / Giove dal cielo ancora quando tuona » (Inf. XXXI, 44-45). Parlando di Nembrotte, il costruttore della Torre di Babele (cfr. Gen 10, 8-10) che è anche il primo gigante da lui incontrato, il nostro poeta dichiara infatti:

« La faccia sua mi parea lunga e grossa
come la pina di San Pietro a Roma;
ed a sua proporzione eran l'altr'ossa. » (Inf. XXXI, 58-60)

La faccia del gigante ha dunque dimensioni paragonabili a quelle della grande pigna di bronzo riscoperta nel Medioevo presso le Terme di Agrippa, che probabilmente decorava in origine il vicino Tempio di Iside al Campo Marzio, dove doveva far parte di una fontana. Ai tempi di Dante si trovava nell'atrio dell'antica Basilica di San Pietro, dove egli la vide durante il pellegrinaggio in occasione del Giubileo del 1300, ma nel 1608 venne collocata alla sommità di una scalinata a doppia rampa progettata da Michelangelo, nel cortile del Vaticano oggi detto appunto "della Pigna". Galileo stima che essa misuri cinque braccia e mezza, cioè circa 3,2 metri.

Ora, sempre secondo Galileo solitamente un uomo è alto otto teste. La statura perfetta, degna di un atleta, sarebbe pari a nove teste, ma Galileo esclude che i giganti siano dotati di un corpo armonico, pensando piuttosto a un corpo da "macho", da "wrestler", a un ammasso di muscoli e di forza bruta. Se teniamo per buona questa descrizione, un gigante risulta essere alto 5,5 X 8 = 44 braccia, ovvero più di 25 metri e mezzo (di Nembrotte riparleremo ancora più avanti).

In una proporzione si sa che il prodotto dei medi è uguale al prodotto degli estremi, e quindi:

Galileo stima in tal modo anche l'altezza di Lucifero. Sempre secondo i canoni artistici del Rinascimento italiano, un braccio è pari a circa la terza parte dell'altezza della persona. Pertanto « il vermo reo che 'l mondo fóra » (Inf. XXXIV, 108) sarà alto come minimo 645,3 X 3= 1936 braccia, cioè 1128,7 metri. Arrotondando per eccesso in base a quanto detto sopra, l'altezza di Lucifero arriva ad oltre 2000 braccia, cioè quasi 1200 metri.

A questo punto, Galileo sa che la distanza tra l'ombelico e la metà del petto è un quarto dell'altezza della persona, pertanto il raggio della Giudecca è di 500 braccia, oltre 290 metri. Dai versi di Dante non si possono arguire le dimensioni delle altre tre zone del Cocito; ma, se anch'esse hanno la forma di sfere, Galileo suppone che esse siano equidistanti fra di loro, come i cieli del Paradiso si circondano l'un l'altro; ed allora la Tolomea avrà un raggio di 1000 braccia, l'Antenora di 1500 e la Caina di 2000 (rispettivamente 583, 875 e 1166 m).

È possibile ripetere calcoli analoghi per le Malebolge, l'ottavo cerchio dell'Inferno nel quale sono puniti i frodatori? Come ora vedremo, ciò è possibile. Questo cerchio è suddiviso in dieci bolge, cioè in dieci fossati concentrici (da cui il termine "bolgia" per indicare una gran confusione), cerchiati da mura e scavalcati da ponti di roccia, simili alle fortificazioni di un castello medievale:

« Luogo è in inferno detto Malebolge,
tutto di pietra di color ferrigno,
come la cerchia che dintorno il volge.
Nel dritto mezzo del campo maligno
vaneggia un pozzo assai largo e profondo,
di cui suo loco dicerò l'ordigno.
Quel cinghio che rimane adunque è tondo
tra 'l pozzo e 'l piè de l'alta ripa dura,
e ha distinto in dieci valli il fondo. » (Inf. XVIII, 1-9)

A questo proposito, è interessante leggere le acute osservazioni di Giorgio di Rienzo (1942-2011), già ordinario di Storia della Letteratura Italiana Moderna e Contemporanea presso l'Università di Torino, esperto di lessicografia computazionale e collaboratore del "Corriere della Sera":

« Nell'ottavo cerchio vengono puniti i fraudolenti, disposti in dieci bolge. Il luogo è detto appunto "Malebolge". Le prime tre terzine descrivono la scena così come appare a Dante, le tre terzine successive cercano invece di darne immagine, attraverso una similitudine terrestre. Ed ecco lo spettacolo che ne risulta. Appaiono dieci profonde valli concentriche all'ultimo pozzo infernale, e a traverso di queste valli si vedono dieci ponti che le sovrastano, che le tagliano per l'intera estensione del cerchio, dalla riva esteriore, fino all'ultima che forma il pozzo centrale. »

Per farci comprendere meglio "l'ordigno", cioè la struttura architettonica di questo postaccio, il nostro Autore ricorre alla similitudine con i castelli cinti da mura, così diffusi ai suoi tempi bellicosi:

« Quale, dove per guardia de le mura
più e più fossi cingon li castelli,
la parte dove son rende figura,
tale imagine quivi facean quelli;
e come a tai fortezze da' lor sogli
a la ripa di fuor son ponticelli,
così da imo de la roccia scogli
movien che ricidien li argini e ' fossi
infino al pozzo che i tronca e raccogli. » (Inf. XVIII, 10-18)

Continua il professor de Rienzo: « La scena è simile a quella che si può vedere, dall'alto, nei castelli cinti di mura e da fossi di difesa, quando su quei fossi, dalla porta alla riva esterna, vadano dei ponti. Tutto all'intorno è pietra color del ferro, ovunque ci sono macigni e anfratti: il luogo dà immagine all'oscurità della frode, alla tortuosità della mente che sa ingannare. »

Quello che più interessa del commento di Giorgio de Rienzo è il capoverso seguente:

« Ma c'è in questa duplice descrizione dantesca anche un desiderio di precisione e di concretezza figurativa, una volontà di esattezza e di simmetria che risultano persino eccessivi. Il contegno si ripete tale e quale più avanti, quando Dante passa nella prima delle dieci bolge dell'ottavo cerchio. Qui il poeta vede una folla di dannati, tormentati da diavoli crudeli e beffardi: e la folla si divide in due schiere, che camminano l'una in senso opposto all'altra; così come camminano - spiega - in due file di folla, sul Ponte di Castel Sant'Angelo, i pellegrini chiamati a Roma dal Giubileo. Tanto più degradante si fa la materia del racconto, tanto più Dante pare attento alla geometria formale. Tutto il Canto XVIII vive su un contrasto assai singolare. Ha una struttura rigida nella sua costruzione, eppure propone uno spettacolo di caos e di degradazione. »

Giustamente questo canto potrebbe essere intitolato "La Geometria e il Caos"! Della Fisica del Caos parleremo in una prossima lezione; per ora, analizziamo la geometria di questa regione. A proposito della nona e penultima bolgia, così parla Virgilio al suo protetto:

« Tu non hai fatto sì a l'altre bolge;
pensa, se tu annoverar le credi,
che miglia ventidue la valle volge. » (Inf. XXIX, 7-9)

Una circonferenza di 22 miglia equivale a circa 36,4 Km, essendo il miglio toscano corrispondente a 1653,61 metri. Di conseguenza, la nona bolgia, quella dei seminatori di discordie e di scismi (quella dunque di Maometto e Alì), viene ad avere un diametro di 7 miglia, cioè di 11,6 Km. Nel canto successivo poi Dante aggiunge:

« S'io fossi pur di tanto ancor leggero
ch'i' potessi in cent'anni andare un'oncia,
io sarei messo già per lo sentiero,
cercando lui tra questa gente sconcia,
con tutto ch'ella volge undici miglia,
e men d'un mezzo di traverso non ci ha. (Inf. XXX, 82-87)

La circonferenza della decima bolgia, quella dei falsari (Gianni Schicchi, Mastro Adamo, Sinone), è dunque di 11 miglia, cioè di 18,2 Km, ed il suo diametro misura 3 miglia e mezzo, cioè 5,8 Km. Ne consegue che la larghezza della nona bolgia è di 1,75 miglia, cioè di 2,9 Km. Supponiamo che tutte le dieci bolge abbiano la stessa dimensione, come è facile assumere; la larghezza totale dell'ottavo cerchio sarà allora di 17 miglia e mezzo, cioè di 28,9 Km. Il diametro della prima bolgia (quella dei ruffiani e dei seduttori come Giasone) risulterà di 38 miglia e mezzo, ovvero di 63,7 Km, e la sua circonferenza sarà di 120,9 miglia, vale a dire di poco meno di 200 Km. Da notare che la decima bolgia ha un diametro molto maggiore di quello della Caina come calcolata sopra (5,8 contro 1,2 Km), il che lascia pensare che le quattro zone del Cocito non abbiano le stesse dimensioni, ma dimensioni decrescenti verso l'interno.

E questa non è l'unica contraddizione nella struttura geometrica dell'Inferno di Dante, così come la si evince dai suoi stessi versi. Pensiamo infatti per un attimo a quell'immenso Lucifero, alto più di mille metri e le cui sei ali si protendono su tutto il Cocito, ghiacciandolo con il proprio incessante moto. Siccome il Principe delle Tenebre ha tre teste (una mostruosa scimmiottatura della Trinità Divina), in ciascuna bocca egli stritola uno dei tre massimi traditori dell'umanità: Marco Giunio Bruto e Caio Cassio Longino, congiurati contro Giulio Cesare, il fondatore dell'Impero Romano, e Giuda Iscariota, colui che tradì Nostro Signore (ed infatti, oltre ad essere maciullato quest'ultimo si ritrova anche la schiena scorticata). Tuttavia ci accorgiamo subito del fatto che l'aguzzino è decisamente sproporzionato rispetto alle vittime: se Belzebù era davvero tanto grande, un solo suo dente avrebbe misurato almeno dieci metri, e sarebbe stato sufficiente per annientare i tre traditori massimi al primo morso. Bisogna dunque supporre che anche le anime di Giuda, Bruto e Cassio fossero viste da Dante più grandi di quanto i tre non fossero stati in vita, onde continuare ad osservare la terrificante scena del Re delle Tenebre che rode in eterno i tre peggiori peccatori della storia.

Non basta. Ripensiamo un attimo ai giganti: come detto sopra, Nembrot appare a Dante alto più di 25 metri, cioè almeno tredici volte più alto di un uomo di statura imponente. « Ed a sua proporzione eran l'altr'ossa. » (Inf. XXXIII, 60), aggiunge il nostro poeta, lasciandoci pensare che il corpo del gigante abbia le stesse fattezze e le stesse proporzioni di un uomo normale; solo, tredici volte più alto del normale. Ora, ciò è manifestamente impossibile, e ci sarà facile provarlo. Consideriamo un uomo normale ed uno identico ad esso, ma 13 volte più alto. Com'è noto, i volumi sono proporzionali ai cubi delle dimensioni lineari, e quindi il volume del colosso sarà 13 x 13 x 13 = 2197 volte maggiore dell'uomo normodotato. Poiché possiamo pensare che la densità di muscoli, ossa, organi, ecc. sia la stessa nei due individui, ne consegue che il gigante dantesco ha una massa 2197 superiore a quella di Dante. Ciò crea un grave problema, perchè il gigante si può sostenere solo grazie alle ossa ed ai muscoli delle sue gambe. E quando le dimensioni aumentano di 13 volte, le superfici aumentano di 13 x 13 = 169 volte, perchè le superfici sono proporzionali ai quadrati delle dimensioni lineari. Dunque Nembrotte è 2197 volte più pesante di Dante, ma le aree delle sezioni delle sue gambe sono aumentate solo di 169 volte, e dunque il gigante non potrebbe camminare. Potrebbe farlo solo se anche l'area della sezione delle sue gambe fosse aumentata di 2197 volte, ma allora il loro diametro dovrebbe aumentare di 47, non di 13 volte (47 è approssimativamente la radice quadrata di 2197). Per questo Nembrotte, Efialte e compagnia dovrebbero avere i muscoli delle gambe così sviluppati, che i loro arti inferiori sarebbero di tre volte e mezzo più larghi rispetto ai nostri; ed essi a Dante apparirebbero terribilmente sproporzionati. Il Ghibellin Fuggiasco avrebbe perciò ragione da vendere quando descrisse così i colossi disposti lungo il pozzo che separa l'ottavo dal nono cerchio dell'Inferno:

« gli orribili giganti, cui minaccia
Giove del cielo ancora quando tuona! » (Inf. XXXI, 44-45)

E non è tutto. Come ha scritto Andrea Delnegro nel suo saggio "La Fisica dei Manga", un altro guaio che i giganti si troverebbero ad affrontare è quello dei tempi di reazione, cioè la velocità di risposta agli stimoli esterni. Diversi studi hanno evidenziato come gli animali piccoli abbiano riflessi molto più rapidi rispetto agli animali di proporzioni maggiori. Ciò è dovuto a un insieme di fattori per i quali gli animali grossi devono gestire movimenti molto più importanti rispetto a quelli più piccoli, i cui movimenti sono decisamente limitati. Senza ombra di dubbio, un gigante alto 25 metri come Nembrot avrà dei tempi di reazione più lenti rispetto a un umano, il quale potrebbe con facilità sfuggire ai suoi assalti, perché una creatura di quelle dimensioni faticherebbe a competere in velocità e destrezza con un umano di taglia normale. Il suo corpo troverebbe maggiori difficoltà a coordinare correttamente i movimenti degli enormi arti e, anche se dovesse riuscirci, impiegherebbe molto tempo a spostare un braccio, dato il peso enorme di esso. Altre ricerche hanno dimostrato che, per muoversi, gli animali di piccola taglia utilizzano sistemi diversi rispetto a quelli con una corporatura superiore. Le creature più ridotte usano i riflessi per spostarsi con rapidità e regolare ogni mossa, mentre quelle grandi si muovono utilizzando una "predizione ipotetica", cioè una previsione di ciò che accadrà in seguito al movimento, per gestire il movimento successivo. Per fare un esempio, mentre il topino che corre può aggiustare il tiro di ogni passo nel giro di qualche decimo di secondo, un elefante, dopo aver messo una zampa in avanti, procede nel successivo spostamento affidandosi alla predizione (o alla speranza) che un simile movimento non incontri intoppi. È un meccanismo apparentemente non privo di rischi, ma utilissimo per gli animali di grossa taglia, che così compensano la maggiore lentezza di riflessi dovuta alle dimensioni. Di conseguenza, anche un gigante di 25 metri utilizzerebbe lo stesso automatismo degli elefanti e delle balene, per l'appunto citati dal Sommo Poeta, e sarebbe davvero troppo lento nei movimenti e nei riflessi. Non è dunque troppo severo il giudizio del noto critico Attilio Momigliano che, come vedremo, in relazione ai giganti del XXXI canto dell'Inferno, ha parlato di « materia enorme e idiota »!

(Per inciso, la parola "gigante", che di solito viene fatta derivare dal greco "Ge", "Terra" e "gao", "nasco", giacché questi colossi era ritenuti figli della dea madre Terra, viene invece da alcuni posta in relazione con il sanscrito "G'antu", cioè "animale", "belva", con il raddoppiamento tipico del greco "gignomai", "partorisco". Anche in questo caso, "nomina sunt omina"!)

A proposito di giganti e delle loro misure, sorge alla mente il dubbio di come Dante indichi il concetto di un numero molto grande. E qui arriva la sorpresa: Dante non va mai al di là del concetto di migliaia. Nell'intera Commedia non troverete mai il concetto di "milione" o di "miliardo", in perfetta sintonia con la mentalità medioevale, ancora legata alla numerazione romana. In latino infatti non esiste un termine specifico per indicare i milioni, i miliardi, e così via: per indicare il numero "un milione" gli antichi Romani dicevano "decies centena milia", cioè "dieci centinaia di migliaia". E così, "un numero enorme" viene reso genericamente dall'Alighieri con "mille" o "più di mille". Vediamone alcuni esempi. Con il semplice concetto di migliaia viene reso il numero delle ombre dei lussuriosi travolte dalla bufera infernale:

« "Vedi Parìs, Tristano"; e più di mille
ombre mostrommi e nominommi a dito,
ch'amor di nostra vita dipartille » (Inf. V, 67-69)

Quello dei diavoli che tentano di sbarrare a Dante e Virgilio l'ingresso nella Città di Dite:

« Io vidi più di mille in su le porte
da ciel piovuti, che stizzosamente
dicean: «Chi è costui che sanza morte
va per lo regno de la morta gente?» (Inf. VIII, 82-85)

Quello delle anime degli epicurei nelle arche infuocate, secondo Farinata degli Uberti:

« Dissemi: "Qui con più di mille giaccio:
qua dentro è 'l secondo Federico
e 'l Cardinale; e de li altri mi taccio" » (Inf. X, 118-120)

Quello dei centauri che sfrecciano le anime degli omicidi immerse nel Flegetonte:

« Dintorno al fosso vanno a mille a mille,
saettando qual anima si svelle
del sangue più che sua colpa sortille » (Inf. XII, 73-75)

Quello dei leoni ammazzati in Africa dal gigante Anteo, almeno nelle parole adulatrici di Virgilio:

« O tu che ne la fortunata valle
che fece Scipïon di gloria reda,
quand' Anibàl co' suoi diede le spalle,
recasti già mille leon per preda » (Inf. XXXI, 115-118)

« Poscia vid' io mille visi cagnazzi
fatti per freddo; onde mi vien riprezzo,
e verrà sempre, de' gelati guazzi » (Inf. XXXII, 70-72)

La quantità dei profumi che, miscelandosi assieme, allietano la Valletta dei Principi:

« Non avea pur natura ivi dipinto,
ma di soavità di mille odori
vi facea uno incognito e indistinto » (Purg. VII, 79-81)

L'intensità del frastuono del quale non si accorge l'uomo che pensa molto, espresso in "unità" di "tube", cioè di trombe, raggiunge ovviamente la quota di mille:

« O imaginativa che ne rube
talvolta sì di fuor, ch'om non s'accorge
perché dintorno suonin mille tube » (Purg. XVII, 13-15)

Il numero di quanti, come Stazio, hanno alimentato il fuoco della loro poesia alla fiamma divina:

« Al mio ardor fuor seme le faville,
che mi scaldar, de la divina fiamma
onde sono allumati più di mille » (Purg. XXI, 94-96)

Quello dei desideri ardenti che costringono gli occhi di Dante a fissare quelli rilucenti di Beatrice, nel Paradiso Terrestre:

« Mille disiri più che fiamma caldi
strinsermi li occhi a li occhi rilucenti,
che pur sopra 'l grifone stavan saldi » (Purg. XXXI, 118-120)

« Vid' io ben più di mille splendori
trarsi ver' noi, e in ciascun s'udia:
Ecco chi crescerà li nostri amori » (Par. V, 103-105)

Quello degli Spiriti che formano la scritta "Diligite ivstitiam qvi ivdicatis terram" nel Cielo di Giove:

« Resurger parver quindi più di mille
luci e salir, qual assai e qual poco,
sì come 'l sol che l'accende sortille » (Par. XVIII, 103-105)

« Sì, soprastando al lume intorno intorno,
vidi specchiarsi in più di mille soglie
quanto di noi là sù fatto ha ritorno » (Par. XXX, 112-114)

« E a quel mezzo, con le penne sparte,
vid' io più di mille angeli festanti,
ciascun distinto di fulgore e d'arte » (Par. XXXI, 130-132)

Dunque Dante Alighieri non conosceva numeri più grandi delle migliaia? Incredibilmente, egli ha trovato il modo per esprimere in modo più circostanziato l'incredibile numero degli Angeli del Paradiso. Se le considerazioni matematiche fin qui esposte non hanno saziato la vostra conoscenza, così come non hanno saziato la mia, cliccate qui per penetrare nel mondo dell'algebra e scoprire in che modo il nostro Autore è riuscito ad esprimere nella Terza Cantica un numero così grande, che la mente umana è incapace quasi di concepirlo!