

Qualcuno potrebbe pensare che, se i fenomeni della natura fossero davvero soggetti alla gravità quantistica, sicuramente i suoi insoliti effetti dovrebbero essere già stati rilevati. Così invece non è perché, come tutti gli incredibili effetti della Relatività Ristretta (contrazione delle lunghezze, dilatazione dei tempi, la relatività della simultaneità, eccetera) si manifestano solo a velocità prossima a quella della luce, che per noi è pressoché irraggiungibile, così tutti gli effetti di natura quantistica della gravitazione sono confinati in una scala di lunghezze e di tempi straordinariamente piccola. Ma piccola quanto?
Max Planck (23 aprile 1858 – 4 ottobre 1947) con Albert Einstein nel 1931
Proponiamoci di cercare un sistema di "unità naturali", basati sulle tre principali grandezze fisiche, e cioè la costante di gravitazione universale G, bastione della Fisica Classica; la velocità della luce c, simbolo della Relatività Ristretta; ed ovviamente la costante di Planck h, o meglio la costante h tagliata pari ad h/2π, caratteristica della Meccanica Quantistica. Come determinare una "unità naturale di lunghezza"? Fissiamoci sulle dimensioni fisiche di queste costanti. La costante di gravitazione G si misura in Newton per metro quadro su kilogrammo al quadrato, quindi:
[ G ] = [ N m2 / Kg2 ] = [ m3 Kg–1 s–2 ]
c è una velocità, per cui [ c ] = [ m s–1 ]. Quanto poi alla costante di Planck:
[ h ] = [ E / f ] = [ J / Hz ] = [ m2 Kg s–1 ]
Se vogliamo combinare queste tre grandezze in modo da ottenere una lunghezza, dovremo moltiplicarle dopo averle elevate ad opportuni esponenti:
E quindi, per le equazioni dimensionali sopra scritte:
![]()
Da cui:
![]()
Se ne deduce che deve essere:
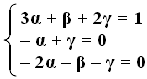
Risolvendo il sistema si ottiene facilmente α = 1/2, β = – 3/2, γ = 1/2. Ne consegue che la nostra equazione dimensionale (1) assume la forma:
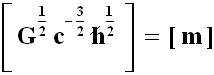
Chiameremo questa lunghezza fondamentale con il nome di lunghezza di Planck lP. La precedente ci dice che la sua espressione è:
ed essa vale lP = 1,616252 x 10–35 m. Analogamente si può introdurre una massa di Planck mP ed un tempo di Planck tP, partendo dalle equazioni dimensionali:
![]()
Le espressioni che si ottengono con calcoli analoghi a quelli ora svolti sono le seguenti:
che valgono rispettivamente mP = 2,17644 x 10–8 kg e tP = 5,39124 × 10–44 s. Si potrebbero introdurre anche una temperatura di Planck e una carica elettrica di Planck, ma in tal caso bisogna introdurre nei calcoli altre due costanti fondamentali: la costante di Boltzmann KB e la costante dielettrica del vuoto ε0.
In pratica, il tempo di Planck è circa 10–44 secondi. La lunghezza di Planck è 1020 volte più piccola di un protone. La massa di Planck è pari a un uovo di pulce, o a 1019 protoni. La carica di Planck è 12 volte minore di quella di un elettrone o di un protone. La temperatura di Planck è pari a circa 1032 Kelvin, e un corpo che la raggiungesse emetterebbe radiazioni con lunghezza d'onda pari alla lunghezza di Planck.
Se si esprimono i parametri fondamentali dell'universo in unità di Planck, saltano agli occhi alcune sorprese. Ad esempio, il numero 1061 esprime sia l'età dell'universo, sia la Costante di Hubble-Lemaître, sia la radice quadrata della Costante Cosmologica in unità tP, ma anche il diametro dell'universo in unità lP e la sua massa in unità mP., e persino l'inverso del quadrato della sua temperatura in temperature di Planck! Inoltre già Arthur Eddington aveva fatto notare che 1040 rappresenta ad un tempo il rapporto tra il raggio dell'universo e quello dell'elettrone, tra la forza elettrostatica e quella gravitazionale agente tra un elettrone e un protone, e la radice quadrata del numero di atomi dell'universo. Il reale significato di queste coincidenze numerologiche però ci sfugge, e forse ci sfuggirà per sempre.
Le tre grandezze espresse dalle (2), (3) e (4) sono dette unità di Planck: esse danno vita a un sistema assoluto di unità di misura. Come si verifica immediatamente, le unità di Planck sono completamente estranee alla fisica di ogni giorno: l'unità di lunghezza lP è dell'ordine dei 10–33 centimetri, e quindi è di 21 ordini di grandezza inferiore al diametro di un nucleo atomico; in altre parole, essa sta alle dimensioni nucleari come le dimensioni dell'uomo stanno a quelle della nostra galassia!
Ma allora, come possono esserci utili unità del genere? È presto spiegato. In meccanica quantistica si definisce lunghezza d'onda Compton di una particella la lunghezza d'onda di un fotone la cui energia è pari a quella della massa a riposo della particella. Usando il formalismo matematico, dovrà essere:
![]()
da cui si ricava che la lunghezza d'onda Compton vale:
Si può assegnare un limite inferiore alla lunghezza d'onda Compton (cioè un limite superiore all'energia di un fotone) se si impone un limite superiore alla massa m della particella. Possiamo pensare ad un limite superiore della massa di una particella quando questa raggiunge le dimensioni di un buco nero, all'interno del quale un fotone resta confinato dal campo gravitazionale. Ora, nel nostro ipertesto dedicato ai buchi neri abbiamo spiegato che, a meno del fattore 2, il raggio di Schwarzschild di un buco nero di massa m è:
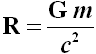
Ricaviamo m da quest'ultima dopo aver posto R = λ e sostituiamola nella (5). Si trova facilmente:
La (6) coincide con la (2) a meno del fattore 2π nella costante di Planck ridotta. Risostituendo tale valore nella (5) si ottiene proprio l'espressione (3), sempre a meno del fattore 2π. Dunque la lunghezza di Planck è la misura del raggio dell'orizzonte degli eventi di una massa di Planck collassata in un buco nero! In altre parole, ogni fotone avente una lunghezza d'onda pari alla lunghezza di Planck può materializzarsi in una particella abbastanza massiccia da diventare un buco nero (detto "buco nero di Planck"), tale da distorcere lo spazio-tempo fino al punto di inghiottire quel fotone. Non possono quindi esistere lunghezze d'onda più piccole di così, perchè altrimenti la particella ottenuta dalla materializzazione del fotone non potrebbe nemmeno sussistere, essendo confinata per sempre all'interno del buco nero in cui essa è collassata! Grazie alla gravità quantistica abbiamo così trovato un limite inferiore per le lunghezze. Questo si traduce ovviamente in un limite inferiore per i tempi, non appena si osserva che la (2) e la (4) sono legate tra di loro da questa semplice relazione:
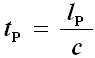
Il tempo di Planck è dunque quello impiegato dalla luce per coprire una lunghezza di Planck; non esistendo nulla che possa andare più veloce della luce, non ha senso pensare a tempi più brevi di tP.
Se non si può ragionare di distanze e tempo inferiori a quelli della scala di Planck, appare evidente che i concetti stessi di spazio e di tempo perdono di significato a quegli ordini di grandezza, e questo è considerato un indizio del fatto che la Meccanica Quantistica e la Relatività Generale non valgono più separatamente; a distanze paragonabili alla lunghezza di Planck quindi la gravità manifesta degli effetti quantistici. Ci conferma però l'impossibilità di accedere sperimentalmente a queste distanze non solo la loro estrema piccolezza, ma anche un'altra considerazione, legata alla cosiddetta energia di Planck EP. Essa rappresenta l'energia equivalente alla massa di Planck secondo la famosa equazione di Einstein EP = mP c2. Si ottiene facilmente:
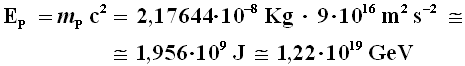
Di qui si ricavano i 1019 GigaelettronVolt citati quando abbiamo parlato della grande unificazione delle forze, indicandoli come l'energia alla quale avviene l'accoppiamento della gravità alle altre tre forze della natura. Come già accennato, però, per verificare sperimentalmente cosa accade a queste energie sarebbe necessario un acceleratore di particelle delle dimensioni della nostra Galassia!

Logo realizzato dalla 2 B Liceo Classico a.s. 2024/25 per un'iniziativa scolastica
Purtroppo queste nuove unità di misura hanno introdotto un grosso problema nella Fisica delle Particelle, il cosiddetto "problema dell'innaturalezza": perché il bosone di Higgs è così "innaturalmente" leggero? Infatti tale particella, come visto, ha una massa di circa 126 GeV, cioè circa 1017 volte (o 100 milioni di miliardi di volte, se preferite) inferiore alla massa di Planck: un valore innaturalmente esiguo, come se in un'equazione che ne determina il valore comparissero numeri enormi che, in modo miracoloso, si cancellano tutti! Provo a spiegarmi meglio. Quando il bosone di Higgs conferisce la massa alle altre particelle, queste ultime gliela "restituiscono" subito: si può cioè scrivere un'equazione per la massa del bosone di Higgs che include un termine per ciascuna particella con cui interagisce. Tutte le particelle del Modello Standard dotate di massa contribuiscono all'equazione, ma non sono gli unici contributi possibili. Infatti il bosone di Higgs dovrebbe anche interagire con tutte le possibili particelle più pesanti, fino a quelle alla scala di Planck. Ma nell'equazione suddetta tali particelle alla scala di Planck (e quindi alle scale di massa e di energia "naturali") dovrebbero fornire contributi enormi alla massa del bosone di Higgs, circa 1017 volte maggiori della sua massa effettiva. Se ne dedurrebbe che il bosone di Higgs sia massiccio come loro, e appesantisca così anche altre particelle elementari. Conclusione: le particelle avrebbero masse troppo elevate per formare gli atomi, e l'universo sarebbe... vuoto. Affinché il bosone di Higgs dipenda da energie enormi ma finisca per essere così leggero, dobbiamo presumere che alcuni dei contributi alla scala di Planck alla sua massa siano negativi mentre altri siano positivi, e che siano tutti tarati nella giusta misura perché si annullino vicendevolmente. Come ha detto lo stesso Peter Higgs, sarebbe come se le correnti d'aria e le vibrazioni di un tavolo si contrastassero a vicenda in modo tale da mantenere una matita in equilibrio sulla punta sopra quel tavolo: un comportamento giustamente definito "innaturale".
Una possibile soluzione elegante a questo problema è rappresentato dalla già citata supersimmetria, che come abbiamo visto raddoppia tutte le particelle elementari esistenti in natura. La teoria supersimmetrica dice che ogni bosone ha un superpartner fermionico, e ogni fermione ha un superpartner bosonico. E siccome bosoni e fermioni contribuiscono rispettivamente in termini positivi e negativi alla massa del bosone di Higgs, se questi termini appaiono sempre a coppie, allora si cancelleranno a vicenda, e il problema dell'innaturalezza sarà risolto. Purtroppo però, mentre scrivo queste righe, non è finora emersa alcuna evidenza sperimentale dell'esistenza di particelle supersimmetriche, ed è seriamente possibile che non esistano proprio.
Negli anni settanta i fisici Kenneth Wilson e Steven Weinberg hanno avanzato un'altra proposta per risolvere il problema dell'innaturalezza: la natura avrebbe una struttura gerarchica che ci permette di descrivere quello che accade su scala più grande, senza sapere che cosa sta accadendo "veramente" su scala molto più piccola. Per esempio, possiamo costruire un modello della dinamica dei fluidi con un'equazione che li tratta come fluidi omogenei, ignorando la complicata dinamica delle molecole che li compongono; essa include un termine che rappresenta la viscosità dell'acqua, un singolo numero che si può misurare su scale macroscopiche e che riassume tutte le interazioni molecolari che si verificano su scala microscopica. Insomma, l'influenza delle singole particelle subisce un "taglio" ("cutoff", in inglese), che la rende superflua. Secondo Wilson e Weinberg, le due scale macroscopica e microscopica si "disaccoppiano" tra loro, il che permette di descrivere con efficacia alcuni aspetti del mondo senza sapere che cosa stia succedendo in profondità alla scala di Planck, a dieci miliardi di miliardi di GeV, dove il tessuto stesso dello spazio-tempo cessa di esistere. « È possibile fare fisica perché possiamo continuare a non sapere che cosa accade sulle brevi distanze », ha spiegato Riccardo Rattazzi, fisico teorico del Politecnico di Losanna. Allora, se il "taglio" del Modello Standard fosse vicino alla scala di Planck, dove si sa per certo che esso viene meno, perché non tiene conto della gravità quantistica), le correzioni microscopiche alla massa del bosone di Higgs sarebbero enormi, rendendo "innaturale" la sua leggerezza. Invece un "taglio" non molto al di sopra della massa del bosone di Higgs lo renderebbe all'incirca pesante quanto le correzioni provenienti dal "taglio", e tutto sembrerebbe ben più "naturale". Questa possibilità è stata il punto di partenza del lavoro svolto negli ultimi quarant'anni nel tentativo di affrontare il problema dell'innaturalezza. In tempi più recenti, i fisici teorici Steven Abel e Keith Dienes della Durham University hanno calcolato che, a causa di una particolare simmetria della teoria delle stringhe chiamata invarianza modulare, le correzioni date dagli stati delle stringhe a tutte le energie tra la scala macroscopica e quella microscopica sarebbero correlate nel modo giusto per annullarsi, mantenendo piccola la massa del bosone di Higgs. Ancora una volta, comunque, a mio avviso la reale soluzione del problema sta nel campo della gravità quantistica, e dunque potremo risolvere tutti i problemi legati all'innaturalezza quando possederemo una teoria quantistica del campo gravitazionale.