Esperienze di Fisica: sulla cresta dell'...onda

	L'ondoscopio è uno strumento che permette di studiare facilmente i fenomeni ondulatori. Come si vede in figura, esso consta di una vaschetta con fondo in plexiglas trasparente, sopraelevata rispetto al bancone del laboratorio mediante zampe di metallo; in essa si versa dell'acqua, poi si pone al pelo del liquido una bacchetta metallica orizzontale sostenuta da elastici, sopra la quale è montato un motorino dotato di massa eccentrica. Qui il dispositivo è scollegato dall'alimentazione ed è poggiato sul bancone del Laboratorio, in attesa di venire utilizzato.
	Come si vede in questa fotografia ripresa dai miei ragazzi della 4 D a.s. 2003/2004, ora l'ondoscopio è stato collegato all'alimentazione: il motorino che fa vibrare la bacchetta orizzontale (vibratore) è alimentato a 5 V in corrente continua, mentre la lampada e l'otturatore che ruota davanti ad essa sono alimentati a 220 V in corrente alternata, Quando il motorino è posto in rotazione, esso oscilla a causa della massa fuori baricentro e produce delle onde sulla superficie dell'acqua. Ma come si fa a visualizzarle?
	Il trucco è presto svelato. Sopra la vaschetta è posto un proiettore, davanti al quale ruota una ventola che fa da otturatore; esso si comporta perciò da stroboscopio. Regolando la corrente che alimenta il motorino del vibratore e quello dell'otturatore, è possibile farli girare con la medesima frequenza; allora le onde proiettate sul bancone appaiono ferme, ed è possibile disegnarle su foglio di carta e misurarne per es. la lunghezza d'onda mediante righello.
	Questa fotografia, ripresa invece da Roberto Carettoni (II B cl. a.s. 2004/05), illustra un ulteriore dettaglio preso dall'alto dello stroboscopio. Come si può vedere, la ventola interrompe il fascio di luce permettendo la facile visualizzazione delle onde in questione. Il principio è lo stesso delle luci psichedeliche di una discoteca.
	Quest'altro particolare, sempre ripreso dall'alunno Roberto Carettoni, illustra invece il procedimento per visualizzare il fenomeno della riflessione: nell'acqua della vaschetta è posta una barretta metallica diritta che fa da specchio piano. In questa foto appare in primissimo piano anche il vibratore ed il motorino con massa eccentrica che lo mette in azione.
	Ecco il risultato di una prima osservazione del fenomeno testé descritte: sul foglio bianco si possono vedere le onde piane riflesse dalla barretta metallica (la foto è della IV D a.s. 2003/04). Riportando tutto su carta è facile verificare come l'angolo d'incidenza risulti congruente all'angolo di riflessione, secondo quanto studiato teoricamente in classe.
	Un'altra foto di Roberto Carettoni che mostra un altro spettacoloso fenomeno: con una sbarretta curva di forma parabolica è possibile osservare le onde piane che divengono sferiche e si concentrano nel fuoco, in accordo con le proprietà della parabola studiate nel corso di Matematica. Qui ci si riallaccia poi ai fari delle automobili ed alle antenne paraboliche sui tetti.
	Inserendo nel vibratore piano un opportuno percussore che termina con una sferetta di plastica o di metallo, si osserva direttamente la formazione di onde sferiche (nel caso specifico, circolari perchè bidimensionali), se ne può misurare la lunghezza d'onda e le si può trasformare in onde piane mediante specchio parabolico. Questa è opera della IV D a.s. 2003/04.
	E' poi possibile inserire nel vibratore piano due percussori a sfera, i quali genereranno onde circolari in fase tra loro (cioè aventi stesso periodo, stessa ampiezza e stessa fase), le quali daranno vita al fenomeno dell'interferenza. Si osservano nitidamente le frange di interferenza distruttiva e costruttiva, avente entrambe la forma di iperboli equilatere.
	Quello che qui vedete fotografato è un modello molto più sosfisticato di ondoscopio, acquistato dal mio Liceo durante la pandemia da SARS-CoV-2 del 2020-21, poiché a quell'epoca per motivi di sicurezza i ragazzi non potevano toccare gli strumenti di laboratorio, e tutte le esperienze andavano svolte esclusivamente da banco. In questo caso i raggi di luce con l'immagine delle onde non vengono proiettati sul bancone, come nel caso precedente, ma attraverso uno specchio inclinato di 45° sono proiettati su uno schermo verticale, e gli alunni possono visionarlo, fotografarlo o filmarlo. In questo modo è possibile evidenziare tutti i fenomeni ondosi già osservati nelle foto precedenti!
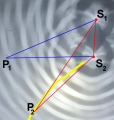	Come si vede, con il precedente ondoscopio è possibile eseguire una verifica quantitativa delle leggi dell'interferenza. Si esegue l'esperimento già descritto sopra, quindi se ne scatta una foto o se ne estrae un frame da un filmato e lo si stampa. E' facile stimare la lunghezza d'onda della luce come distanza tra due frange scure, poi si evidenziano le frange di interferenza costruttiva a forma di iperbole, se ne sceglie un punto P, si misurano le distanze dalle due sorgenti P1 e P2, e si verifica se la differenza \| PS1 – PS2 \| è o meno un multiplo intero di una lunghezza d'onda. Straordinariamente efficace, no?
	In realtà, la fisica delle onde che si propagano nell'acqua è molto complicata, dato che la loro propagazione, usata (come ad esempio nell'ondoscopio) quale esempio principe di fenomeno ondulatorio, è assai diversa da quella delle onde sonore o luminose. Per studiare la propagazione delle onde nel mare può esserci di grande aiuto Google Earth, il celebre programma che offre immagini della Terra dallo spazio. Osserviamo ad esempio qusest'immagine...
	...e quest'altra, che rappresentano un'insenatura del Mar Mediterraneo presso Alessandria d'Egitto (le coordinate sono 31° 12' 28.56'' N, 29° 53' 34,66'' E). La precedente è stata presa il 20/9/2010, quella qui a fianco il 14/12 successivo. In entrambe è facile ravvisare il fenomeno della diffrazione: le onde piane che incidono sull'imboccatura del golfo si trasformano in sferiche, perchè l'insenatura ha dimensione comparabile con la loro lunghezza d'onda!
	Questo terzo esempio di utilizzo didattico di Google Earth mostra lo stesso fenomeno, stavolta ripreso il 14/12/2010 a Théoule-sur-Mer, nel sud della Francia (coordinate 43° 31' 54.86'' N, 6° 56' 59.41'' E): le barriere di protezione dei porti e delle spiagge (qui evidentissime!) trasformano le onde piane che arrivano parallelamente alla costa in onde circolari, provocando una caratteristica erosione della spiaggia a forma di semicerchio!
	L'erosione della spiaggia dovuta alle onde sferiche diffratte dalle barriere di protezione è particolarmente visibile a Campo di Mare, in provincia di Brindisi (coordinate 40° 32' 27.33'' N, 18° 04' 09.17'' E, foto scattata il 14/12/2010). I frangiflutti hanno letteralmente modificato la forma della costa, permettendo di ampliare notevolmente la superficie della spiaggia. In questo modo ogni studente può rendersi conto di come le onde possono aggirare gli ostacoli.
	Questo particolare notevolmente ingrandito di una nave nei pressi della costa meridionale di Cipro (coordinate 34° 56' 27.21'' N, 33° 39' 17.36'' E, foto scattata il 7/7/2007 è un altro eccezionale esempio di come, attraverso il fenomeno della diffrazione, le onde possono girare attorno agli ostacoli che incontrano. Ciò spiega perchè noi possiamo sentir parlare una persona, anche se essa si trova in un'altra stanza: la sua voce aggira il bordo della porta!
	Ultimo esempio di diffrazione delle onde: questi frangiflutti a La Grande-Motte, nella regione della Linguadoca-Rossiglione, in Francia (coordinate 43° 33' 18.71'' N, 4° 05' 20.01'' E, scattata il 21/8/2006). Oltre alla suddetta caratteristica erosione semicircolare della spiaggia, qui si possono vedere le onde del Mediterraneo aggirare i frangiflutti, e raggiungere ogni angolo della spiaggia!
	Qui vediamo un fenomeno diverso, l'interferenza tra fronti d'onda circolari generate dalle aperture nelle barriere di protezione della spiaggia. Ci troviamo a Rimini il 28/5/2002 (coordinate 44° 05' 15.02'' N, 12° 32' 26.07'' E). È possibile anche osservare il fenomeno della riflessione delle onde circolari sulla spiaggia; le onde riflesse a loro volta interferiscono con quelle entranti attraverso le barriere, rendendo assai arduo descrivere correttamente questo moto ondoso.
	Il fenomeno dell'interferenza tra onde sferiche in fase tra di loro è ancor meglio osservabile in questa foto da satellite che raffigura la costa davanti a Bangkok, capitale della Thailandia (coordinate 13° 36' 40.11'' N, 100° 34' 46.60'' E), ripresa da satellite il 4/11/2010. La sovrapposizione di una cresta con una gola tende a cancellare l'onda (interferenza distruttiva), mentre la sovrapposizione di due creste o di due gole la amplifica (interferenza costruttiva).
	Il fenomeno della riflessione delle onde marine (oltre a quello della diffrazione) è perfettamente visibile a Port Elizabeth in Sudafrica, in questa foto scattata il 24/2/2007 (coordinate 33° 57' 19.98'' S, 25° 38' 33.05'' E). L'onda resa sferica dal frangiflutti va ad incidere sulla spiaggia, e qui si riflette indietro, sotto forma di un'onda sferica il cui centro di propagazione sembra trovarsi al di là dell'ostacolo.
	Qui invece siamo a Londra, sul Tamigi, nel dicembre 2006 (coordinate 51° 29' 42.06'' N, 0° 03' 37.86'' E). La scia lasciata da un'imbarcazione si è letteralmente riflessa su questo ostacolo. Gli studenti possono verificare con questo strumento le leggi della riflessione: l'angolo di incidenza delle onde è congruente all'angolo di riflessione!
	Nell'immagine a sinistra potete vedere l'interferenza tra i fronti d'onda di due scie, fotografate il 6/11/2006 sempre lungo il Tamigi (le coordinate esatte sono 51° 27' 40.79'' N, 0° 16' 05.69'' E). Ricordiamo che, se l'acqua è molto bassa, cioè quando la profondità h è minore della lunghezza d'onda λ, la velocità delle onde nell'acqua può essere ricavata estraendo la radice quadrata del prodotto tra la profondità h e l'accelerazione di gravità g.
	Quello che qui vediamo fotografato da satellite il 28/4/2002 presso Villaricos in Andalusia (coordinate 37° 14' 04.59'' N, 1° 47' 04.79'' E) è il fenomeno della rifrazione: se le onde raggiungono una zona dove l'acqua è più bassa, l'attrito con il fondo le fa rallentare, la loro lunghezza d'onda diminuisce ed esse cambiano direzione di propagazione. Insomma, qualunque sia l'angolo con cui le onde si avvicinano alla spiaggia, esse tendono a rifrangersi e ad arrivare sempre parallele ad essa!
	Altro straordinario esempio di rifrazione delle onde, stavolta ripreso in Sardegna il 18/8/2010 (coordinate 39° 46' 12.64'' N, 8° 27' 28.82'' E). Lo strumento "righello" di Google Earth permette di misurare la distanza tra due punti geografici; grazie ad esso gli studenti possono misurare la lunghezza d'onda e calcolare la velocità delle onde, che in acqua profonda è circa pari alla radice quadrata della lunghezza d'onda per l'accelerazione di gravità diviso due pi greco. Se λ = 100 m, v = 12,5 m/s.
	Ed eccoci a Chichiriviche, in Venezuela, nell'aprile 2006 (coordinate 10° 55' 29.88'' N, 68° 15' 26.93 W). Anche in questo caso l'avvicinarsi delle onde a fondali più bassi fa inclinare variamente i loro fronti d'onda. Qui inoltre è possibile osservare insieme i fenomeni della rifrazione, della riflessione sulle coste e sulle scogliere e dell'interferenza fra le onde dirette e quelle riflesse!
	Questa fotografia ci introduce all'acustica: ecco due diapason con relativo martelletto ed una canna labiale. I diapason (dal greco "per mezzo di tutte", cioè accordo ottenuto per mezzo di tutte le frequenze) vibrano su una nota fissa (770 Hz) e vengono perciò usati per accordare gli strumenti musicali, inoltre la disposizione in figura permette di studiare il fenomeno della risonanza (percuotendo l'uno, inizia a vibrare anche l'altro). invece la canna labiale permette, soffiando nell'ancia, di emettere note di diversa altezza variando la lunghezza della cannula. Un'esperienza davvero divertente!
	L'immagine in figura ritrae un diapason elettromagnetico. Si tratta di uno strumento analogo a quello riportato sopra, però,a differenza di quello, è formato da un'elettrocalamita e da un diapason, che fanno parte di uno stesso circuito. Chiudendo il circuito con una pila, l'elettrocalamita attira uno dei rebbi provocando l'apertura del circuito. Ma in tal modo il circuito si apre, l'elettrocalamita si disattiva, il rebbio ritorna nella posizione iniziale chiudendo il circuito e facendosi attirare nuovamente dall'elettrocalamita e così via, facendo sì che il suono prosegua finché prosegue l'alimentazione elettrica.
	Quest'esperienza è vivamente consigliata ogni volta che si illustra i fenomeni ondosi a ragazzi delle elementari e delle medie. In pratica si prende un diapason, si appoggia un foglio di carta sulla sua cassa di risonanza e vi si dispone della limatura di ferro. Quindi si percuote il diapason, e si vedrà la limatura di ferro "ballare" sul foglio di carta, sollevata dalle vibrazioni cui la cassa di risonanza è sottoposta (una mia collega ha usato addirittura la metafora della limatura che "frigge"). Sicuramente un modo semplice per spiegare il concetto di onda; ecco a voi anche un breve filmato digitale che illustra quest'esperienza.
	Quello che si vede in questa fotografia è il dispositivo utilizzabile per dimostrare l'esistenza delle onde stazionarie. Cosa sono? Percuotendo un oggetto si provoca un moto che, se non ci fosse l’attrito, sarebbe armonico, ed ogni punto, oscillando, induce quelli vicini a fare altrettanto, generando un’onda che si propaga lungo tutta la corda fino ad uno dei due estremi fissi, dove si riflette generando una seconda onda che si propaga in verso opposto. Il moto di un punto dell'oggetto è quindi il risultato della sovrapposizione di due onde: una progressiva ed una regressiva. La loro sovrapposizione dà vita ad un'onda in cui tutti i punti sono o in fase o in opposizione di fase, l’onda non si propaga più e viene chiamata stazionaria.
	I punti dell'onda stazionaria che non oscillano mai, avendo ampiezza di oscillazione costantemente pari a zero, si dicono nodi dell'onda. Per visualizzarli si una lamina quadrata di metallo scuro su cui viene distribuita della sabbia finissima (vedi foto precedente). Se si percuote un angolo della lamina, si osserva come i granelli di sabbia tendano ad addensarsi lungo una croce che divide la lamina in quattro parti uguali; questo perchè l'onda stazionaria ha lunghezza d'onda pari al lato della lamina, e di conseguenza i nodi stanno esattamente alla mezzeria di essa!
	Se invece di percuote il centro di un lato, si produce un'onda stazionaria diversa, in cui i nodi coincidono con i punti delle diagonali della lamina. Da notare che, continuando a percuotere la lamina, i granellini di sabbia rimasti fuori dalle diagonali continuano ad oscillare su e giù, mentre quelli nelle diagonali (sui nodi) non si muovono: come volevasi dimostrare! Di questa espeerienza è disponibile anche un breve filmato digitale.
	Un'altra esperienza classica, di sicuro effetto fin dalle scuole elementari: il campanello sotto la campana a vuoto. In pratica dentro la campana a vuoto è montato un campanello messo in azione grazie ai cavi elettrici visibili in figura. Lo si attiva, in modo che gli studenti odano chiaramente il tintinnio, quindi si comincia ad estrarre l'aria da sotto la campana mediante la pompa a vuoto (vedi meccanica); mano a mano che l'aria esce, ci si accorge che il suono della campana non risulta più udibile, perchè viene a mancare l'aria che trasporta le onde sonore. Semplice, no?
	Quello illustrato in figura è un telefono rudimentale che tutti possono costruire. Basta prendere due bicchierini di plastica (in questo caso due bicchierini dello yogurt) e collegarli con un lungo filo fissato dentro il fondo bucato dei bicchierini mediante un nodo. Come mostrano le due studentesse fotografate, se si allontanano di parecchi metri ed una parla a bassa voce nel suo bicchierino, l'altra sentirà tutto ponendo il proprio vicino all'orecchio, perchè le onde sonore si propagano molto meglio in un mezzo solido (la cordicella) che non nell'aria!
	Lo strumento qui visibile è normalmente chiamato stetoscopio (dal greco "osservazione del petto", anche se più propriamente lo si dovrebbe chiamare stetofonendo, cioè "ascolto del petto"), ed è stato ideato nella sua forma attuale biauricolare nel 1851 da Arthur Leared (1822-1879). Il principio è lo stesso del telefono precedente: una struttura a disco percepisce i battiti cardiaci, che vengono trasmessi ed amplificati da un canale che si biforca e giunge alle orecchie del medico. Strumento davvero storico, oggi è stato per lo più sostituito da strumenti elettronici di grande precisione.
	Questo flauto di Pan (dal nome del dio greco che lo avrebbe inventato) serve non già per suonare agresti melodie, ma per mettere in evidenza il rumore di fondo. Infatti tutti noi siamo immersi in un sommesso rumore di sottofondo, ed accostando l'orecchio via via alle varie canne si odono tonalità diverse di esso, per via della loro lunghezza e quindi della loro diversa risonanza. Questo è anche il motivo per cui, accostando l'orecchio a una conchiglia, sembra di udire in essa il rumore del mare: tutto effetto del rumore di fondo!!
	Uno strumento acustico davvero interessante è il tubo di Quincke qui riprodotto. Il suono, raccolto dalla tromba, viene suddiviso nei due tubi e torna a riunirsi presso l'auricolare dalla parte opposta. Allungando uno dei due rami come si fa con un trombone, cambia la lunghezza dei due percorsi e si verificano dei suggestivi fenomeni di interferenza acustica, con il suono che si affievolisce per certe lunghezze e si potenzia per altre.
	Ed ecco un metronomo (dal greco métron, misura e nómos, regola), strumento familiarissimo ai musicisti, perché serve a indicare lo stacco del tempo nell'esecuzione musicale e a tenere il tempo durante le esecuzioni; esso è formato da un doppio pendolo, messo in movimento da un meccanismo regolabile ad orologeria. Normalmente si ritiene che esso fu brevettato a Parigi da un certo Johann Nepomuk Maelzel di Ratisbona; indispensabile in ogni lezione di acustica musicale.
	Questo è un monocordo, utilizzabile per esperimenti relativi all'altezza del suono. Esso dispone di una corda oscillante, che emette un'onda sonora in funzione della tensione e della lunghezza. Il ponte mobile può essere spostato, e ciò permette di variare l'altezza delle note emesse dall'acuto al grave.
	Un altro pezzo da museo: una cassa di distribuzione per canne sonore. In pratica la si collega ad un turboventilatore ed essa fornisce aria a delle canne metalliche, ciascuna delle quali emette note di frequenza diversa in relazione alla lunghezza, allo spessore, al materiale, eccetera (esattamente come corde diverse, se pizzicate, emettono note di altezza diversa). Se il monocordo è il prototipo ideale degli strumenti a corda, questo alimenta tutti i prototipi di strumenti a fiato.
	Questo invece è un vero flauto di Pan realizzato dal nostro tecnico di laboratorio Elio Tagliaferro con le sue mani. Esso ha quindici canne e quindi può emettere altrettante note. Mentre nel flauto usuale le note diverse vengono emesse chiudendo i diversi fori con le dita, qui non ci sono fori, e le note vengono emesse soffiando in successione nelle diverse canne. Questo strumento musicale è tipico della Svizzera Tedesca e delle regioni andine del Sudamerica.
	Non potevano mancare le campane tubolari, tipico strumento a percussione costituito da lunghe barre metalliche cave che vengono accordate modificando la lunghezza. Sono suonate colpendole con un martello. Lo strumento nella sua forma attuale fu ideato nel 1886 da John Hampton; sono utilizzate ad esempio nella Nona Sinfonia di Mahler. Si può osservare che ogni campana ha una lunghezza diversa dalle altre, ed è proprio questa caratteristica a produrre le diverse note!
	Ed ecco un vero strumento a fiato; e che strumento! Si tratta dell'organo del santuario di S.Maria a Brunello (VA), il cui rettore è mio amico e mi ha concesso di pubblicare questa foto. L'organo è, come si suol dire, uno "strumento aerofono a tastiera"; anche il pianoforte è a tastiera, ma si tratta di uno strumento a percussione perché i tasti azionano dei martelletti che percuotono le corde. Invece nell'organo l'aria compressa generata da mantici è inviata attraverso le canne d'ottone, e la loro intensità è per l'appunto regolata mediante tasti. Secondo la tradizione l'organo fu inventato dal greco Ctesibio che realizzò un organo idraulico, alimentato cioè ad acqua.
	Dopo uno strumento a fiato, ecco uno strumento a percussione: si tratta della batteria con la quale diversi studenti si sono esibiti durante la festa di fine anno scolastico il 10/6/2006. Il nome significa "gran quantità" di pezzi d'artiglieria, provenendo dal linguaggio militare, ma è passato ad indicare sia il complesso di più pile (batteria elettrica), sia il complesso di più tamburi, piatti ed altre percussioni che possiamo vedere in figura. Complimenti al suonatore!
	Quella che vedere a fianco è l'analisi, eseguita mediante un oscilloscopio, dei battimenti generati da due diapason che vibrano con frequenze molto vicine tra loro. La loro interferenza dà vita a un'onda portante che viene distintamente avvertita come un suono separato. La musica ha fatto spesso uso dei battimenti, com'è il caso del celebre "Trillo del diavolo" di Giuseppe Tartini (1692-1770)!
	Un pezzo che non può mancare in questo Laboratorio Virtuale è il fonografo, l'antenato dei nostri lettori CD. Inventato da Thomas Alva Edison nel 1877, consiste in una puntina che legge un disco di vinile (alcuni sono visibili sulla destra), il cui solco trasmette alla puntina un moto ondulatorio poi trasformato in onde sonore da un dispositivo elettromagnetico. I dischi di vinile a 33 e a 45 giri sono tuttora ricercatissimi dai collezionisti.
	Un'esperienza suggestiva può essere realizzata con questo generatore di frequenze collegato ad un altoparlante: agendo opportunamente sulle monopole è possibile far emettere all'amplificatore tutto lo spettro delle frequenze dagli infrasuoni agli ultasuoni, e così verificare che il campo di udibilità umana va da 16 a 16.000 Hz circa!
	La strana trombetta illustrata in figura è un emettitore di microonde. Le microonde sono onde elettromagnetiche la cui lunghezza d'onda è compresa fra un millimetro e un metro; per questo esse si distinguono, a seconda della lunghezza d'onda, in onde millimetriche, centimetriche e decimetriche. Di solito vengono utilizzate nei ponti radio e per trasmettere comunicazioni telefoniche multiple e segnali televisivi. Le microonde si prestano a vari esperimenti didatticamente interessanti come la verifica della loro interferenza, diffrazione e polarizzazione (vedi subito sotto).
	Lo strano oggetto in figura, visto di fronte e di taglio per visualizzarlo meglio, è una lente di paraffina. Sì, avete capito bene: una lente come quella dei nostri occhiali, come evidenzia soprattutto la vista di taglio, usata per mostra la rifrazione delle microonde, nonchè per dimostrare che esse subiscono gli stessi identici effetti palesati dalle onde luminose che attraversano le comuni lenti di vetro. Solo, le sue dimensioni e la sua distanza focale sono assai maggiori di quelle delle lenti degli occhiali, perchè la lunghezza d'onda delle microonde è maggiore della lunghezza d'onda della luce! Il diametro è di circa 30 cm.
	Questo sembra il coperchio di un tombino, invece è un apparecchio didatticamente assai importante: una griglia di polarizzazione per microonde. Se la si frappone tra un emettitore ed un ricevitore di microonde in modo che le sbarre siano parallele alla loro direzione di polarizzazione, le onde passano interamente; se la si ruota di 90°, non passa assolutamente nulla, dimostrando che le microonde sono polarizzate, hanno cioè una direzione preferenziale di oscillazione!
	Qui vediamo un alimentatore per klystron. Per chi non avesse mai sentito questa strana parola, derivata dal greco klyster (siringa) e dall'inglese electron (elettrone), dirò che si tratta di un tubo elettronico utilizzato per generare oscillazioni ad altissima frequenza, corrispondenti a onde decimetriche o centimetriche, e quindi a microonde. Il klystron è quindi utilizzato principalmente nei trasmettitori e nei ricevitori radar.
	Questa fotografia davvero straordinaria, scattata dal guardiamarina John Gay della US Navy, rappresenta un aereo supersonico, e precisamente un F/A-18 Hornet, nel momento in cui esso abbatte il muro del suono. Le onde sonore da esso emesse si appiattiscono in avanti a causa dell'effetto Doppler e producono uno strato che l'aereo deve distruggere per superare Mach 1. La violenta decompressione provoca la condensazione del vapor d'acqua nella nuvoletta qui visibile!
	Torniamo a Google Earth per illustrare il fenomeno dell'onda conica. Consideriamo la scia lasciata da questa barca nel Tamigi presso Londra il 6/11/2006 (coordinate 51° 28' 05.40'' N, 0° 15' 18.12'' E). Se un corpo si muove in un mezzo a una velocità maggiore del suono in quel mezzo, le onde sonore sferiche "restano indietro" e danno vita a un'onda di questo tipo, a forma di cono. Il "Bang" supersonico è costituito proprio da questa onda!
	Cosa c'entra la foto di questa papera, ripresa a Sesto Calende (dove il lago Maggiore si restringe fino a diventare il fiume Ticino) la sera del 25/7/2020? C'entra perchè, come si vede nell'immagine sottostante, la sua scia può essere costruita tramite l'inviluppo delle onde circolari da essa prodotte nell'acqua, giacché la papera si muove nell'acqua più velocemente delle onde stesse! Si tratta della stessa "onda conica" che, generata da un aereo, prova il famoso "Bang supersonico"!
	Con questa immagine lasciamo l'acustica ed entriamo nel dominio dell'ottica. Tale scienza fu avviata da Isaac Newton con la sua fondamentale opera « Optiks ». Prima di lui Galileo Galilei aveva tentato la misurazione della velocità della luce facendo scoprire una lanterna ad un suo discepolo spedito su una collina lontana, ma la distanza era troppo breve, e si misurava solo il tempo di reazione del braccio dell'assistente. La velocità della luce fu misurata per la prima volta da Ole Roemer nel 1675.
	La bellissima fotografia in figura illustra nel miglior modo possibile la formazione di raggi luminosi, e quindi la propagazione rettilinea della luce. Il sole occhieggia infatti da dietro una nuvola e produce un fantastico arabesco nel cielo. Newton, con il suo modello corpuscolare, spiegava la propagazione rettilinea mediante il principio d'inerzia applicato ai corpuscoli dei quali sarebbe fatta la luce; Huygens invece, con il suo modello corpuscolare, la spiegava sostenendo che un'onda si propaga in un mezzo uniforme in modo che i raggi (linee perpendicolari ai fronti d'onda) risultino rettilinei.
	Questa fotografia, scattata dall'autore di questo sito nella cucina di casa sua, mostra di nuovo la propagazione rettilinea della luce. Stavolta i raggi luminosi sono diventati visibili perchè in cucina è stata cotta una bistecca sulla piastra, fatto che ha saturato l'atmosfera di fumo. Le particelle di fumo rifrangono i raggi luminosi, e così diventa particolarmente evidente la propagazione della luce sotto forma di traiettorie rettilinee!
	Altra esperienza che è facilissimo svolgere in qualunque ambiente (qui nella cucina di casa mia il 6/1/2005): quella detta del "bastone spezzato". Basta introdurre in un bicchiere d'acqua un cucchiaio, ed esso apparirà come se fosse rotto in due. A provocare questo scherzo è il fenomeno della rifrazione della luce nel passaggio dall'aria all'acqua. Guardando il bicchiere dall'alto, il fenomeno è ancora più evidente! Un'esperienza che mi è stata mostrata fin dalle scuole elementari...
	Gli oggetti si distinguono in opachi (la luce non li attraversa), trasparenti (la luce li attraversa facilmente) e traslucidi. Questi ultimi vengono attraversati dalla luce, ma attraverso di essi si può distinguere solo la maggiore o minore luminosità, non le forme degli oggetti. Questo è il caso dei vetri montati sulle bocche di lupo di questa cantina.
	In questa foto vedete ritratti due ripiani del nostro Armadio Virtuale, sui quali sono posti in bella vista alcuni specchi sferici per esperienze di ottica. Con essi è possibile verificare la costruzione dell'immagine generata da uno specchio sferico di piccola curvatura seconda le leggi dell'ottica geometrica, un argomento purtroppo trascurato nelle odierne lezioni di Fisica, e che invece io giudico didatticamente molto utile per mostrare la strettissima interconnessione tra Geometria teorica e Fisica osservativa.
	Questa fotografia illustra una facile esperienza, utile per illustrare anche ai bambini il fenomeno della riflessione della luce. Basta aprire un contenitore di CD ad angolo retto in modo che la facciata trasparente stia davanti a una candela accesa. Interponendo un bicchiere di vetro tra la candela accesa ed i nostri occhi si potrà vedere la fiamma bruciare dentro il bicchiere. Infatti l'immagine che si vede nel contenitore proviene sia dalla candela che dalla luce riflessa dal bicchiere; facendo sovrapporre le due immagini, il cervello le percepisce come se provenissero da una sola sorgente, quella che si vede nel bicchiere!
	Questa invece l'ho scattata durante un'eclisse parziale di sole, l'11 agosto 1999, eci mostra che straordinari giochi di luce ha provocato il sole eclissato tra le fronde degli alberi del mio giardino (visibili anche in un particolare della foto precedente E' un evidente applicazione del fenomeno che sta alla base del funzionamento della camera oscura e, quindi, della macchina fotografica!
	La camera oscura, che è alla base del funzionamento delle comuni macchine fotografiche, è una scatola in cui è stato praticato un buchetto detto foro stenopeico (dal greco "stretto foro"), il quale proietta sulla faccia opposta la luce, come un obiettivo, dando vita a un'immagine. Con la camera oscura si possono eseguire molti esperimenti spettacolari, tra i quali l'osservazione di un'eclisse di sole. Come è noto, fissare questo raro e magnifico fenomeno astronomico può causare gravi danni permanenti alla vista; tuttavia, durante l'eclissi parziale di sole del 29 marzo 2006, mi è bastato proiettare l'immagine del sole sul fondo della camera oscura per vedere chiaramente il suo disco ridotto ad una mezzaluna, come mostra il riquadro!
	Un'interessante applicazione della camera oscura è l'elioscopio, che vedete raffigurato in questi scatti del mio studente Davide Ferrari (2 C a.s. 2021/22). Il 24 marzo 2022 ho fatto costruire ai miei studenti di seconda delle camere oscure con materiale povero (scatole di cartone, carta oleata, nastro adesivo), quindi li ho portati nel parcheggio del Liceo, e siccome la mattinata era calda e assolata, ho detto loro di puntare il foro stenopeico verso il Sole, facendo attenzione a non guardarlo mai direttamente. Come si vede, sulla carta oleata si proietta l'immagine del disco solare; misurandone il diametro con un calibro ventesimale e facendo ricorso ad una semplice proporzione, è immediato stimare con una certa precisione la misura del diametro del Sole. Enjoy it!
	Non c'è nulla meglio di questo stereovisore anni '70 per illustrare il fenomeno della visione binoculare: di due immagini uguali il cervello ne fa una sola. Funziona come i proiettori sottostanti, ma non ha lampadine e basta puntarlo verso una fonte di luce.
	Questa magnifica lanterna magica è di proprietà del mio alunno Gabriele Bof (2 G a.s. 2012/13), che possiede davvero un piccolo museo di curiosità tecnologiche. Si tratta dell'antenato dei moderni proiettori di diapositive, in grado di proiettare immagini dipinte su vetro sopra uno schermo in una stanza buia, tramite una scatola chiusa contenente una candela; la luce di quest'ultima passa attraverso una lente che permette la messa a fuoco. La più antica descrizione di una lanterna magica la si trova nell'"Ars Magna Lucis et Umbrae" (1646) del gesuita Athanasius Kircher, ma essa era già nota ad arabi e cinesi.
	La foto di Marta Milano mostra uno strumento ottico che si incontrava in ogni scuola ed in molte case, prima dell'avvento dei computer e delle fotocamere digitali: un proiettore, che funziona grazie ad una sorgente di luce e ad un abile gioco di lenti.
	Un modello più perfezionato di proiettore, che proietta film e non solo diapositive, è quello qui illustrato: ha la forma di una valigia perchè proprio dentro una valigia viene trasportato comodamente. Inoltre esso è in grado di riprodurre anche l'audio, grazie ad un lettore magnetico e ad un sistema di altoparlanti. Una rivoluzione, rispetto al modello precedente!
	Un altro proiettore, sempre fotografato dalla cortese Marta Milano, ma stavolta per filmati in formato super 8 o superotto, un tipo di pellicola cinematografico a passo ridotto, e quindi adatto sia per riprese che per riproduzioni amatoriali. Per questo un tempo quasi tutti i filmati di argomento scientifico da proiettare nelle scuole erano realizzati con questa tecnica; naturalmente, prima che le cassette VHS ed i DVD rivoluzionassero l'Home Theatre!
	Può essere considerato un proiettore anche questa lavagna luminosa, particolarmente adoperata nelle scuole e nelle università per proiettare lucidi, cioè testi, grafici ed immagini riprodotte su fogli di plastica trasparente. Una lampadina posta sotto il piano di vetro proietta verso l'alto l'immagine riprodotta sul lucido, questa si riflette sullo specchio inclinato di 45° (ma di inclinazione regolabile) e va a disegnarsi sullo schermo o su una parete bianca. Sono stati approntati persino dei particolari schermi trasparenti per Pc, così da proiettare direttamente le schermate. Il diffondersi delle presentazioni in Power Point e dei proiettori digitali ha mandato in pensione questi storici accessori.
	Ed ecco per l'appunto un moderno proiettore digitale: è ancorato al soffitto e proietta direttamente le immagini provenienti da un computer. Si noti che esso è dotato di tre proiettori, ciascuno con i tre colori fondamentali: rosso, verde e blu. La sovrapposizione delle immagini dei tre colori permette di ricostruire le immagini che noi possiamo ammirare sullo schermo. Sovrapponendo i tre colori con la stessa identità si ha il bianco.
	Quelli ritratti sulla sinistra di questa fotografia sono degli occhialini tridimensionali, utilizzati per ottenere una visione stereoscopica di una foto come quella dell'astronauta ripresa sulla destra. Il trucco è semplice: una "lente" degli occhialini è rossa, l'altra è blu, cosicché l'occhio sinistro vede solo la parte d'immagine stampata in rosso e l'occhio destro solo quella stampata in blu, leggermente traslata rispetto all'altra. Il cervello sovrappone le due immagini e genera l'illusione stereoscopica.
	Il parallelepipedo qui a fianco, a quattro facce, può essere utilizzato per una versione semplificato dell'esperimento di Foucault per la misura della velocità della luce. Lo si pone in rapidissima rotazione e si fa incidere su di esso un fascio di luce, trasmesso attraverso uno specchio semiargentato, e lo si fa poi riflettere su di esso per mezzo di uno specchio convesso. Si osserva che esso viene riflesso all'indietro in una posizione diversa da quella di partenza, a causa della rotazione dello specchio avvenuta mentre il raggio di luce si propagava. Dall'angolo di deviazione si ricava la velocità della luce. In figura è visibile anche un prisma pieno di liquido, per studiare le proprietà della rifrazione.
	Alcune esperienze molto semplici sulla propagazione luminosa possono essere eseguite con una bacinella d'acqua in cui viene sciolto un po' di detersivo in polvere, in modo da visualizzare meglio un fascio di luce laser, visibile anche fuori dall'acqua se uno studente diffonde polvere di gesso nell'aria sbattendo tra loro due cancellini. Qui si può verificare intuitivamente sia la propagazione rettilinea del raggio di luce rossa, sia la sua rifrazione nel passaggio dall'aria all'acqua!
	Con lo stesso sistema è facilissimo visualizzare il fenomeno della riflessione totale: se l'angolo di incidenza supera l'angolo limite, il raggio di luce viene riflesso completamente nel mezzo di partenza (fenomeno su cui si basa il funzionamento delle fibre ottiche). In questo caso, il raggio di luce rossa torna a riflettersi all'interno della bacinella d'acqua!
	Sulla riflessione totale si basa anche il il periscopio, un tubo alle cui estremità sono posti dei prismi di vetro inclinati di 45° rispetto alla verticale. Quelli più complessi permettono una visione a giro d'orizzonte, mantenendo nascosto l'osservatore. Il primo utilizzo del periscopio sembra vada attribuito a Johann Gutenberg, l'inventore della stampa, che lo usò per consentire ai pellegrini di vedere sopra le teste della folla ad una festa religiosa svoltasi ad Aquisgrana nel XV secolo. Oggi i periscopi sono utilizzati nei sottomarini per guardare al di fuori del pelo dell'acqua.
	Una scatola "a sorpresa", che contiene un ampio kit per eseguire esperienze con i raggi luminosi. A sinistra si vede il proiettore (il parallelepipedo nero, alimentato da corrente a 12 V), a destra c'è il goniometro di plastica bianca, mentre tutt'attorno si vede un ampio campionario di specchi, prismi e lenti per lo studio dell'ottica geometrica.
	Questa foto scattata da Marta Milano (III B cl. a.s. 2004/05) rappresenta il semplice proiettore della fotografia soprastante, in grado di proiettare dei fasci luminosi paralleli, in modo da mostrare il potere convergente di una lente biconvessa in plexiglas. Si osserva come i raggi non convergano in un solo fuoco, ma diano vita a una curva detta caustica di rifrazione.
	Un'altra foto della stessa autrice, che stavolta ha "catturato" la verifica quantitativa delle leggi della riflessione, secondo le quali il raggio incidente, quello riflesso e la normale alla superficie riflettente sono complanari, e l'angolo di incidenza è congruente a quello di riflessione. La superficie riflettente è uno specchietto diritto, e la misura degli angoli viene facilmente effettuata con il goniometrico di plastica.
	Stavolta qui la signorina Milano ha ripreso la verifica quantitativa delle leggi della rifrazione, secondo le quali il raggio incidente, quello riflratto e la normale alla superficie rifrangente sono complanari, ed il rapporto tra il seno dell'angolo di incidenza e quello dell'angolo di rifrazione è costante e pari all'indice di rifrazione (legge di Snell). La verifica è effettuata mediante un prisma di plexiglas, per cui si misurerà l'indice di rifrazione relativo del plexiglas rispetto all'aria.
	Altra foto della stessa autrice, che ha misurato l'indice di rifrazione aria-acqua. Per questo scopo basta sostituire il prisma di plexiglas dell'esperienza precedente con una scatoletta piena d'acqua. Nulla vieta di riempirla di alcool, olio, benzina, ecc. per misurare l'indice di rifrazione di vari materiali.
	Il medesimo apparato (proiettore e goniometro) delle fotografie precedenti permette la verifica della formazione dell'immagine in uno specchio concavo, ottenuto piegando una lamina metallica (le mani sono quelle della prof.ssa Claudia Bina). Anche in questo caso i raggi convergenti danno vita ad una curva complicata detta caustica di riflessione.
	Questo, realizzato dai nostri studenti, è un semplicissimo esempio di specchio cilindrico, costruito incollando fogli di alluminio da cucina su cartoni di rotoli di carta. Come si vede chiaramente, essi consentono di realizzare una "anamorfosi", cioè un immagine visibile solo da un particolare punto di vista. Quadrettando un disegno (in questo caso un uccellino) e riportandolo su una mezza corona circolare, una volta posto lo specchio cilindrico al centro di essa, l'uccellino torna perfettamente visibile nelle sue esatte proporzioni!
	Ed ecco uno specchio sferico, da me fotografato in un centro commerciale. Come si vede, l'intero panorama viene compresso in uno spazio ristretto, distorcendolo fortemente verso i bordi. È lo stesso principio su cui si fondano i cosiddetti obiettivi ad occhio di pesce, in grado di abbracciare un panorama a 180°, a patto di accettare distorsioni sui bordi. Il primo di questi obiettivi, il Robin Hill Sky, fabbricato dalla ditta Beck di Londra, fu ideato per studiare le formazioni di nubi riproducendo su una singola lastra un'immagine di tutto il cielo.
	Il mirascopio è, come dice il nome, uno strumento concepito per realizzare miraggi, ossia immagini virtuali di oggetti esistenti ma posti in un diverso punto dello spazio. Esso è costituito da un contenitore con le pareti interne costituite da specchi concavi simmetrici, e da una capsula di forma emisferica da porre al centro di essi. All'interno del mirascopio, in questo caso, viene posta una raganella di plastica, posta esattamente sotto la capsula. Grazie ai due specchi concavi posti uno di fronte all'altro, l'oggetto posto sullo specchio inferiore viene riflesso al centro del foro...
	...e l'immagine tridimensionale di esso si forma sulle pareti della capsula! Tale immagine è un vero e proprio ologramma (immagine tridimensionale) ed è visibile da qualunque direzione, come mostra il particolare ingrandito! Se però si cerca di toccarlo con un dito, ci si rende conto che... non esiste, e che si tratta di un miraggio a tutti gli effetti! Infatti la particolare forma degli specchi concavi riflette sulla capsula ogni particolare dell'oggetto all'interno, ricostruendone l'aspetto!
	Un altro "giocattolo" che però può insegnarci molte cose sull'ottica. Questo "cubo magico" (come lo hanno battezzato i suoi creatori) sembra avere all'interno un cubo blu... sospeso a mezz'aria. E non basta: quando si infila in esso una moneta, essa letteralmente... svanisce! Si tratta in realtà di un gioco di specchi: uno specchietto è disposto a 45° lungo la diagonale di due facce opposte del cubo, e le monete infilate in esso finiscono in realtà nello spazio al di sopra dello specchio. Inutile dire che anche il cubo appare sospeso a mezz'aria grazie a questo gioco di riflessioni...
	Ecco a voi un caleidoscopio (dal greco "vedere bello"), antico giocattolo formato da un tubo di plastica rivestito internamente di specchi montati in modo da formare tra loro angoli di 60°; nella parte anteriore sono inseriti dei frammenti di plastica colorata di varie forme e tonalità. Appoggiando l'occhio ad un'estremità e ruotandone la parte terminale mobile, è possibile vedere delle figure geometriche simmetriche colorate, prodotte dall'unione dell'immagine diretta dei frammenti e di quelle create dalle riflessioni negli specchi; le figure cambiano colore e forma, senza mai ripetersi! Nel riquadro se ne vede un esempio.
	Ecco un modo alternativo di realizzare un caleidoscopio, stavolta di grandi dimensioni. Abbiamo preso tre tavole di compensato uguali tra loro, le abbiamo unite tramite cerniere snodabili e vi abbiamo incollato tre specchi, quindi le abbiamo richiuse a formare un triangolo equilatero. All'interno abbiamo posto dei triangolini di legno a vivaci colori. Sbirciando all'interno del prisma di legno così ottenuto, ecco le meravigliose figure generate dal fenomeno della riflessione della luce!
	Quello che qui vediamo fotografato è un simpatico giocattolo che permette di realizzare in modo estremamente semplice dei... disegni animati. Si tratta di un cilindro girevole all'interno del quale viene inserita una striscia di carta che porta rappresentati alcuni fotogrammi, cioè dei disegni che differiscono tra loro solo per qualche particolare e che, visti in successione, in questo caso rappresentano una giraffa che corre. Facendo girare rapidamente il cilindro, attraverso le fessure si vedrà l'animazione della giraffa che corre, come mostra questo breve video. Ciò per via della persistenza dell'immagine sulla retina!
	L'immagine a fianco riproduce un utilissimo ed ingegnoso strumento per verificare le leggi della riflessione e della rifrazione della luce. Gli specchi sono girevoli ed orientabili secondo angoli perfettamente misurati dal goniometro; mediante un piccolo proiettore come quello illustrato nella figura soprastante, è facile verificare che l'angolo di incidenza è pari a quello di riflessione, e che gli angoli di incidenza e di rifrazione sono legati tra loro dalla legge di Snell.
	Ed ecco come lo strumento soprastante può essere utilizzato per verificare che l'angolo di incidenza è congruente all'angolo di riflessione: basta puntare un raggio laser verso lo specchietto centrale e verificare dove il raggio riflesso colpisce uno schermo. Si noti che non si vede il raggio, ma solo il punto in cui esso colpisce lo schermo, perchè non vi è dispersione laterale delle onde luminose!
	E ora, il gioco delle immagini multiple. Per effettuare questo gioco occorrono due specchi uguali montati su telaietti metallici incernierati lungo un lato, in modo che si possano aprire a libro, come in figura. In questo primo caso tra i due specchi esiste un angolo di 180°; in pratica è come se fossero un unico specchio, e si ottiene una sola immagine riflessa (si noti l'atmosfera "da Notte di Natale" della foto in questione e delle due successive!)
	Disponiamo ora i due specchi in modo che formino un angolo di 90°. Come si vede, stavolta si formano tre immagini riflesse: oltre alle due immagini prodotte dai due specchi se ne aggiunge una terza, prodotta dai raggi luminosi che si riflettono due volte sui nostri specchi! Da notare che 90° è un quarto dell'angolo giro, e in totale mi sembra di vedere quattro fiammelle.
	Se infine gli specchi sono disposti a formare un angolo di 60°, otteniamo cinque immagini riflesse: due prodotte dai raggi che si riflettono una volta, due dai raggi che si riflettono due volte, e una quinta formata dai raggi che si riflettono tre volte! Da notare che 60° è un sesto dell'angolo giro, e in totale mi sembra di vedere sei fiammelle. Sulla molteplicità delle immagini riflesse da due specchi piani è fondato il caleidoscopio.
	Un fenomeno molto curioso è la riflessione infinita, che si verifica quando due specchi sono posti l'uno davanti all'altro. In questo caso sono una vetrata e uno specchio a riflettere moltissime volte la luce di alcuni lampadari. In realtà l'aggettivo "infinita" è scorretto, in quanto le immagini progressivamente si indeboliscono e si estinguono, a causa dell'assorbimento della radiazione luminosa da parte delle superfici riflettenti!
	Cos'ha di speciale questa foto di un bellissimo cielo azzurro? Proprio l'azzurro del cielo. Infatti sulla Luna e nello spazio il cielo appare assolutamente nero; perchè sulla Terra no? Perchè la Terra è dotata di atmosfera, e le gocce d'acqua e i granelli di polvere che la compongono diffondono in special modo i raggi blu, mentre si lasciano attraversare dagli altri colori. Sulla Luna la luce del sole non può interagire con l'atmosfera semplicemente perchè l'atmosfera non c'è. Questo fenomeno può essere riprodotto versando poche gocce di latte in un bicchier d'acqua, facendo attraversare l'acqua dalla luce di una torcia ed osservando che la luce assume una colorazione bluastra.
	« Ecco, pongo il mio arco sulle nubi ed esso sarà il segno dell'alleanza tra me e la terra »(Genesi 9,13). Questo racconto eziologico, incluso nel primo libro della Bibbia, spiega in maniera popolare l'origine dell'arcobaleno. Oggi sappiamo che questo bellissimo fenomeno atmosferico è dovuto proprio alla rifrazione e alla riflessione totale della luce solare attraverso le minutissime gocce d'acqua sospese nell'atmosfera subito dopo un temporale. I colori in realtà non sono sette ma, siccome ad ogni frequenza luminosa corrisponde un colore diverso, essi sono praticamente infiniti, e sfumano l'uno nell'altro con continuità.
	Come vedete dalla foto accanto, scattata nel giugno 2021, è possibile ottenere il doppio arcobaleno anche artificialmente, facendo rifrangere la luce del Sole attraverso le minutissime goccioline d'acqua disperse nell'aria bagnando il prato in una giornata d'estate! Di questo semplice esperimento è disponibile anche un video, che potete visionare cliccando qui.
	Dalla finestra di un aereo (come nella foto a sinistra) o dalla cima di una montagna può capitare di osservare un curiosissimo "arcobaleno circolare" noto come "la gloria", al cui centro c'è un'immagine dell'osservatore medesimo, in questo caso l'aereo. La causa di questo fenomeno che ha un che di fantasmatico è stata compresa solo di recente, ed è complicata: sono minuscole gocce d'acqua sospese nell'atmosfera a riflettere, rifrangere e diffrangere la luce del sole in direzione opposta al sole.
	Ed ecco un magnifico scatto di Sandro Degiani, eseguito nell'estate 2009 nelle isole Seychelles. Si vede un magnifico tramonto che sembra opera di un pittore: l'intensa colorazione rossa è dovuta al fatto che i raggi del sole sono molto obliqui e, in queste condizioni, il pulviscolo atmosferico diffonde solo la componente rossa della luce solare. Magnifico, eh?
	Come simulare la luce rossa del tramonto in laboratorio? Basta disciogliere poche gocce di latte in una vaschetta d'acqua come quella in figura, e poi osservare la luce di una torcia elettrica che vi passa attraverso. Si noterà come, lateralmente, viene diffusa una luce rossastra, perchè il latte disciolto ha lo stesso identico effetto sulla luce del pulviscolo atmosferico!
	Il 27 ottobre 2004 ci fu un'eclisse totale di luna (vedi) che colorò il nostro satellite di rosso, come mostra questa fotografia ripresa da Fred Espenak L'insolito colore è dovuto ad un fenomeno di rifrazione e di diffusione della luce solare attraverso l'atmosfera terrestre, con il risultato che la componente rossa della luce è proiettata dentro il cono d'ombra della Terra. In pratica questo colore rosso è lo stesso che la luce del tramonto ha proiettato sul condominio di una fotografia soprastante!
	Una fotografia davvero eccezionale, ripresa in Finlandia nel 1992: essa rappresenta il leggendario raggio verde che viene prodotto dal sole un attimo prima di tramontare, e dura solo pochissimi secondi. L'incredibile fenomeno è dovuto alla dispersione dei raggi solari da parte dell'atmosfera, che agisce come un prisma, poiché lo strato di aria che la luce deve attraversare è più spesso al tramonto.
	Jim Kirkpatrick ha scattato questa veduta del lago Tahoe in Nevada nel febbraio 2000, "catturando" un altro impressionante gioco di luce nel cielo: un pilastro solare, fenomeno dovuto alla riflessione dei raggi solari su lontani cristalli di ghiaccio che piovono dalle nubi. Complimenti al fotografo!
	La foto a fianco invece è stata scattata dal sottoscritto alla periferia del mio comune natale, e mostra il curiosissimo fenomeno del miraggio: la strada in lontananza sembra bagnata, perchè riflette le immagini degli alberi e delle auto. In realtà l'inganno è dovuto al fatto che gli strati d'aria più vicini al suolo sono più caldi e quindi meno densi, e dunque rifrangono i raggi di luce, che sembrano provenire dal basso. Avvicinandosi agli oggetti in questione si osserva infatti che l'asfalto è asciuttissimo!
	Ed ecco un cristallo di spato d'Islanda, così detto dalla terra dove fu scoperto, in grado di produrre il fenomeno detto della "doppia rifrazione", scoperto dal danese E. Bartholinus nel XVII secolo. Se posto al di sopra di una scritta, attraverso di esso questa apparirà leggibile due volte! Di questo minerale riparleremo anche nell'Armadio Virtuale di Geologia.
	Questo è un collage davvero eccezionale di illusioni ottiche. Le linee in alto a sinistra sono parallele, anche se non sembra; il cerchio in alto a destra è assolutamente fermo, anche se l'occhio lo vede muoversi; quella in basso a sinistra è la testa di una lepre o di una papera? Gli altri due oggetti in basso al centro e a destra sono assolutamente "impossibili", anche se il nostro cervello non se ne rende conto. Potete scaricare altri esempi come questi di illusioni ottiche cliccando qui.
	Ed ora, un piccolo enigma che sicuramente vi appassionerà. Questa foto non è una fake, è stata scattata in un luogo realmente esistete, non è stata sottoposta a Photoshop nè ad altro tipo di fotoritocco. Eppure, appare come un paradosso, mostrando una pietra sospesa apparentemente a mezz'aria in una posizione assolutamente innaturale. Eppure, come diceva il Mago Silvan, il trucco c'è anche se non lo si vede. Se volete conoscere la divertente soluzione di questo piccolo enigma ottico, cliccate qui!
	La gif animata a fianco, invero piuttosto insolita,è stata realizzata da me stesso usando due riprese di un quadretto che tengo a capo del letto, a sua volta realizzato con una cartolina "double face" acquistata il giorno stesso della mia laurea, il 22/2/1995. A seconda della direzione da cui la si osserva, si vede il volto dell'uomo della Sindone ed una sua ricostruzione pittografica. Il trucco è presto svelato: l'immagine è impressa su una carta zigrinata le cui linee in rilievo presentano parti di un'immagine su un lato e parti dell'altra sull'altro. A seconda di come si riflette la luce, il nostro occhio ricostruisce un'immagine intera per volta...
	Ed ecco uno dei primi esemplari di immagine double-face come la precedente, risalente al 1593 e conservato presso il Museo Galileo di Firenze, dove è stato fotografato dalla mia allieva Sara Scampini (5 G a.s. 2011/12). Se la miniatura viene guardata dall'alto verso il basso in avanti, sulle facce visibili delle stecche dipinte appare il ritratto del duca Carlo III di Lorena; se, tramite lo specchio posto di fronte, viene osservata dalla parte opposta, la tavola mostra invece il ritratto della Granduchessa Cristina di Lorena, figlia di Carlo III e moglie di Ferdinando I de' Medici: una curiosità scientifica realizzata per divertire gli annoiati signorotti del tardo Rinascimento.
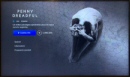	A volte un'immagine ha un aspetto se la si guarda da lontano, e tutt'altro se la si guarda da vicino. E talvolta questo effetto è sfruttato dall'arte, dal cinema o dalla pubblicità. É precisamente il caso di questa immagine di lancio del telefilm horror "Penny Dreadful", una produzione anglo-statunitense di notevole successo andata in onda tra il 2014 e il 2016: vista da lontano, come nel riquadro piccolo, sembra di scorgervi un teschio mostruoso, ma ingrandendo il tutto ed osservandolo da vicino, si vede cge in realtà si tratta del corpo di un uomo visibilmente terrorizzato. Davvero una scelta di grande effetto grafico!
	Quest'immagine, inviatami dall'amico Marco Fontana, rappresenta sicuramente una delle più astute trappole in cui il nostro occhio (e il nostro cervello) possano cadere. Si tratta di una cosiddetta immagine ibrida: cliccateci sopra e, osservandola dalla distanza di un normale schermo Pc, vedrete il volto di Albert Einstein; ma, allontanandovi di 4 o 5 metri o rimpicciolendo l'immagine qui a fianco, vedrete il volto di Norma Jeane Baker alias Marylin Monroe. Perché? Perchè le foto ibride combinano una foto a bassa lunghezza d'onda con una ad alta lunghezza d'onda, foto che il nostro occhio mette a fuoco a diverse distanze, generando la stupefacente illusione. Questa è stata realizzata dal Dr. Aude Oliva per New Scientist Magazine del 31/3/2007.
	Un'altra spettacolare illusione visiva è rappresentata da questa doppia immagine,che dobbiamo a Richard Russell, psicologo dell'Harvard University,. Il volto a destra è percepito come maschile e quello a sinistra come femminile, ed invece entrambi sono versioni dello stesso volto, in tutto e per tutto identiche a eccezione tranne per il fatto che il contrasto tra occhi e bocca e il resto del volto è più alto per la faccia sinistra. Se ne deduce che il contrasto è un indizio importante per determinare il sesso di un volto: con un basso contrasto, i volti sembrano maschili; con un alto contrasto, sembrano femminili. Ciò spiega perché le donne si scuriscono occhi e bocca con i cosmetici: un volto truccato sembra più femminile di un volto senza trucco!
	Concludiamo la galleria delle illusioni ottiche con questo dipinto veramente eccezionale. Se lo osserverete fissamente, vi accorgerete immediatamente che le ellissi sembrano ruotare attorno al loro centro, mentre invece è ovvio che esse sono assolutamente immobili: è il cervello umano che riceve l'"impressione del movimento" dalla particolare disposizione delle bande colorate, e rimane ingannato. Una dimostrazione ulteriore del fatto che a vedere non è l'occhio, bensì il cervello!
	L'occhio umano, come mostrano gli esempi precedenti, è facilmente ingannabile. Ciò avviene perchè il cervello umano cerca istintivamente di individuare forme conosciute e familiari anche nel caos più completo; questo processo prende il nome di pareidolia. Così, noi tendiamo a riconoscere volti o animali nelle nuvole, un volto umano nella Luna (ne parla anche Dante) o immagini familiari nelle costellazioni. Lo stesso fenomeno consente di spiegare presunte apparizioni di fantasmi su muri o fotografie. Eccone un esempio eclatante: nella foto del focolare da me stesso scattata, appare facilissimo riconoscere l'immagine di un diavolo cornuto! Potete scaricarne altri esempi cliccando qui. Ma c'è qualcuno, come invece la mia cara amica Elena Cristina Bolla, che vi vede invece una figura femminile graziosamente inclinata in avanti e di lato. Perchè non una Madonna?
	Il 15 giugno 2017, presso la veranda di casa mia che dà sul giardino, ho trovato in terra una strana macchia di umidità. L'ho osservata più e più volte da tutte le angolazioni, poi ho deciso di fotografarla. Voi che ne dite, avevo ragione di stupirmi? Il fenomeno mentale della pareidolia ha colpito ancora: nulla ovviamente questa chiazza d'acqua ha in comune con la penisola coreana, eppure la somiglianza è davvero impressionante! La pareidolia poi può essere usata anche per realizzare spiritose scenette...
	Quest'altra immagine pareidolica mi è stata inviata dall'amica Elena Cristina Bolla, che condivide con me la passione per questo genere di fotografie. Il gioco di riconoscere immagini di vario genere nelle nuvole è antichissimo, ma in questo caso la pareidolia salta all'occhio, potendo riconoscere un viso umano in quello che è semplicemente un ammasso di vapore acqueo. La mia amica Cristina sostiene di scorgervi il profilo di un angelo; io invece vi scorgo il profilo di Silver Surfer, personaggio dell'universo Marvel creato nel 1966 da da Stan Lee e Jack Kirby. In particolare è impressionante la somiglianza con il Silver Surfer visto nel film "I Fantastici Quattro e Silver Surfer" (2007). Voi che ne dite?
	Ed ecco a voi un'altra curiosa pareidolia: nelle sere di Agosto 2021 mi sono rivisto le puntate dell'"Eneide" televisiva del 1971 con Giulio Brogi. Ebbene, dopo di allora mi sono accorto, guardando fuori dalla finestra del tinello nelle notti di fine estate, che un curioso gioco dei rami e delle foglie degli alberi del mio giardino sotto i raggi di luna sembrava disegnare il profilo del famoso cavallo di Troia che emergeva da dietro le fronde con la sua mole ingannatrice! Davvero curioso, non trovate?
	Ennesimo, strabiliante caso di pareidolia, fotografato nella mia camera da letto. Come si vede, dal bordo del mio letto un volto inquietante sembra curiosare in casa mia. Questo volto potrebbe ricordare la satanica suora del film horror "TheNun - La vocazione del male" (2018)... Ma niente paura: nessuna apparizione demoniaca in camera mia, ma solo un inganno del nostro cervello che cerca a tutti i costi di riconoscere forme note nel caos assoluto, come dimostra la foto a destra, in cui è ripreso lo stesso angolo del mio letto, visto però da un'altra angolazione: il demone in abito da suora è scomparso!
	Insistiamo con i casi di pareidolia da me osservati nella vita quotidiana. Guardando il film di fantascienza "Planet of Dinosaurs" (1977) diretto da James K. Shea ho osservato, del tutto involontariamente, una gran quantità di pareidolie nel paesaggio roccioso dell'ipotetico pianeta alieno. In realtà il film è stato girato nel Vasquez Rocks Natural Area Park, nella Sierra Pelona (California), location di molti film e serie televisive. Conclusione: le rocce possono assumere forme davvero bizzarre, e dunque anche le celebri pietre di Marcahuasi in Perù non sono sculture scolpite ottomila anni fa, come sostengono esoteristi ed ufologi, ma semplici rocce modellate dal vento!
	Persino questo contenitore di auricolari wi-fi per smartphone può rappresentare un incredibile esempio di pareidolia, stavolta nel mondo dei fumetti, perchè ad osservarlo da questa angolazione esso somiglia in maniera straordinaria al celeberrimo viso di Donald Duck alias Paperino!
	Le pareidolie sono spesso sfruttate da divertenti meme come quello che vedete qui a fianco, e che girava in rete tempo fa. In questo caso l'autore ha creato una pareidolia... geografica giocando con le coste dell'Australia, e facendo notare che esse ricordano il muso di un cane ad ovest e quello di un gatto ad est! Cliccando qui potrete vedere un'altra pareidolia geografica, che gioca stavolta con i confini del continente americano! Del resto, non è per via di una ben nota pareidolia, che l'Italia è comunemente conosciuta come "lo Stivale"?
	Cosa c'entra in questa galleria l'affresco di fine '500 di Bonaventura Salimbeni ritratto qui a fianco, raffigurante la Santissima Trinità e visibile nella chiesa di San Pietro a Montalcino (Siena)? Vedete, esse divenne piuttosto noto negli anni settanta perchè alcuni ufologi vi riconobbero un satellite artificiale, di forma sferica, con due antenne simmetriche e persino un oblò in basso a sinistra, vista la sua somiglianza con lo Sputnik 1, lanciato dall'Unione Sovietica il 4 ottobre 1957! In realtà la pareidolia ha colpito ancora: come ben spiegato in questa pagina web, il presunto "Sputnik" è in realtà il globo terrestre, le due "antenne" solo gli scettri regali impugnati dal Padre e dal Figlio come in molti altri dipinti analoghi, l'oblò è in realtà la Luna e la luce di posizione in alto è il Sole!
	La foto che vi propongo è stata da me scattata la sera del 4 aprile 2020, e mostra i cosiddetti "orb", piccoli globi di luce che talora compaiono nelle foto scattate in notturna. Scambiate dagli esoteristi per fantasmi o per creature spirituali, in realtà sono dovute alla luce intensa emessa dal flash che colpisce le particelle di pulviscolo, polline o umidità fluttuanti nell'aria; esse ne riflettono una gran parte generando sfere di luce evanescenti (le particelle sono molto vicine all'obiettivo, e perciò non sono a fuoco) e dai bordi frastagliati (per via delle asperità sulla superficie delle particelle). Conclusione: altro che spiriti... (ecco la stessa foto a flash spento!)
	Quella che il sottoscritto tiene in mano nella figura è una fibra ottica. Si tratta di un sottile filamento di materiale vetroso, eccezionalmente trasparente (sarebbe possibile vedere la luce di una candela attraverso uno strato di 100 Km di questo materiale!), in grado di trasportare attraverso la sua lunghezza un segnale luminoso. La trasmissione avviene attraverso il fenomeno della riflessione totale: il raggio di luce continua ad essere riflesso all' interno della fibra, superando l'angolo limite. Come si vede nell'ingrandimento, anche torcendola la luce la attraversa comunque!
	La foto mostra proprio un fascio di fibre ottiche. Sono flessibili, immuni ai disturbi elettrici ed alle condizioni atmosferiche più estreme, e poco sensibili a variazioni di temperatura; hanno le dimensioni di un capello e sono leggerissime, perché una singola fibra pesa circa 20 kg/km compresa la guaina che la ricopre! I primi a rendersi conto che ess possono essere un mezzo pratico di comunicazione furono Charles K. Kao della STC e George A. Hockham del British Post Office nel 1965.
	Questo invece è un simpatico soprammobile realizzato con un fascio di fibre ottiche: nella base c'è una lampadina la cui luce si diffonde attraverso tutta la lunghezza delle fibre fino all'altra estremità, e il colore che cambia ad intervalli di tempo regolari fa somigliare il soprammobile ad un mazzo di fiori decisamente futuribili. Cliccando qui potrete scaricare un breve filmato che mostra la caratteristica propagazione della luce attraverso queste fibre.
	Lo strumento qui fotografato non può mancare in nessuna collezione, né tantomeno nel Laboratorio Virtuale « Ettore Majorana »: si tratta del banco ottico, un'asta millimetrata sulla quale possono essere montati lenti, specchi, schermo e proiettore per eseguire esperienze di ottica, come la verifica della legge dei punti coniugati. Qui il proiettore genera un fascio di luce cilindrico e quindi un'immagine circolare sullo schermo bianco, opportunamente messa a fuoco.
	Per poter eseguire la verifica della legge dei punti coniugati (1/p + 1/q = 1/f) è meglio disporre di un'immagine che può essere messa a fuoco più facilmente. Per questo, facciamo ricorso ad un otturatore con una sottile fessura verticale, ben visibile in questa foto che ritrae il proiettore del banco ottico collegato all'alimentatore (vedi l'Armadio di Elettromagnetismo). Si potrebbe anche fare ricorso ad otturatori con la forma di frecce, cuoricini, triangolini o anche più fantasiosi: meglio definita è l'immagine e più facile sarà metterla a fuoco sullo schermo spostando quest'ultimo (cioè variando q tenendo fisso p).
	Ed ecco il risultato dell'esperienza con il banco ottico: il fascio di luce attraversa la lente e proietta un'immagine a forma di astina sullo schermo, che qui è stato spostato fino a metterla a fuoco. Si noti che la misura di p è pari alla distanza dell'otturatore del proiettore dalla lente, e quindi per misurarla si ricorre ad un artificio: si allontana la lente dal proiettore di una lunghezza pari a quella di un'astina la cui misura è perfettamente conosciuta e pari quindi a p, mentre q è misurata sulla riga millimetrata.
	Un altro modo, ancora più semplice, di realizzare la stessa esperienza è quello, qui illustrato, che adopera una semplicissima candela di cera. In pratica si prende una lente convergente (cioè biconvessa), la si fissa davanti a uno schermo e si cerca la posizione della candela nella quale la fiamma viene messa a fuoco, cioè appare sullo schermo nitida e, ovviamente, capovolta (come si vede nel particolare ingrandito). Si cambia poi la distanza della lente dallo schermo, e si cerca la nuova posizione della candela in cui la fiamma appare a fuoco. In tal modo verificare la legge dei punti coniugati è uno scherzo.
	Questa fotografia illustra tutti gli accessori necessari per le esperienze con il banco ottico: un vasto set di lenti convergenti e divergenti (se ne contano ben 31, più quella montata sul banco per l'esperienza), di proiettori (ben cinque), di otturatori e di strumenti come i filtri di polarizzazione che vedremo subito sotto.
	Ed ecco a voi due cannocchiali costruiti dagli studenti del mio Liceo in occasione di una mostra dedicata a Galileo Galilei nel gennaio 2012. Ideato nel 1608 dall'ottico olandese Hans Lippershey (1570-1619) ma perfezionato da Galileo Galilei, il cannocchiale galileiano è composta da una lente convergente come obiettivo e da una divergente come oculare, poste all'estremità di un tubo in modo che i loro fuochi coincidano. L'immagine prodotta è diritta, ma il campo visivo è assai ristretto.
	Non poteva certo mancare questa splendida foto di una ricca collezione di cannocchiali galileiani, conservati presso il Museo Galileo di Firenze, foto inviatami dalla mia allieva Sara Scampini (5 G a.s. 2011/12). Intuito il potenziale di tale strumento, Galileo costruì il suo primo cannocchiale agli inizi di luglio del 1609, e nel giro di pochi mesi ne realizzò ben 60 esemplari, superiori a quelli olandesi per qualità delle lenti e per ingrandimenti (arrivavano fino a 30!)
	Questa foto la devo alla cortesia della mia studentessa Beatrice Fior (4 C a.s. 2017/18), che ha partecipato all'allestimento di una mostra didattica legata ai laser. Qui si vede Beatrice eseguire per i miei studenti un'esperienza facile e di sicuro successo: si punta un fascio di luce ordinaria contro uno schermo e se ne misura l'intensità con una app sullo smartphone. Non è difficile rendersi conto che, raddoppiando la distanza dalla sorgente, l'intensità della luce si riduce ad un quarto!
	In questo caso invece ad essere puntato verso lo schermo è un laser: siccome il fascio di luce è molto collimato, non si hanno dispersioni e la legge dell'inverso del quadrato (la stessa che regola le interazioni gravitazionali ed elettrostatiche) non vale più: l'intensità della luce laser è la stessa anche raddoppiando la distanza dalla sorgente!
	Ed ecco un luxmetro, strumento digitale utilizzato per misurare l'illuminazione: esso contiene una cella fotovoltaica che produce una corrente elettrica, misurata da un galvanometro. Il lux è l'unità di misura dell'illuminamento, cioè del flusso luminoso per unità di superficie (lumen al metro quadrato). la luce diurna del Sole mediamente varia tra i 32.000 e i 100.000 lux.
	Ed ecco i suddetti filtri di polarizzazione. Sono due strumenti ottici in grado di polarizzare la luce visibile, cioè di "filtrare", e quindi di lasciar passare, solo la luce in cui il campo elettromagnetico vibra in un ben determinato piano, parallelo all'asse ottico del filtro e detto piano di polarizzazione. La sua direzione è variabile facendo ruotare un'apposita levetta lungo il bordo. I filtri sono due per eseguire le esperienze che vedremo immediatamente.
	In questo caso i due filtri di polarizzazione, con le levette bianche che mutano il piano di polarizzazione ben in evidenza, sono stati montati sulla struttura del banco ottico per utilizzarli più agevolmente; occorre solo aggiungere lo schermo bianco dietro di essi per aumentare il contrasto. Si noti che il fenomeno della polarizzazione è sfruttato nei cosiddetti occhiali Polaroid (nome commerciale), che attenuano la luce solare semplicemente selezionando quella che vibra lungo un ben preciso asse ottico.
	Come si vede, la luce che attraversa il filtro è effettivamente attenuata, proprio come attraverso degli occhiali da sole! Se gli assi ottici dei due filtri sono tra loro paralleli, tutta la luce li attraversa senza sforzo, proprio come un foglio di carta cade attraverso due grate solo se le loro sbarre sono disposte parallelamente le une alle altre: lo si vede bene in questa fotografia (le posizioni delle levette non ingannino, perchè non corrispondono alle direzioni dei rispettivi piani di polarizzazione). Se faccio passare la luce di un laser attraverso i due filtri, in questo caso essa raggiunge tranquillamente lo schermo, benché attenuata.
	Se però ruoto l'asse ottico del secondo filtro di 90°, come mostra chiaramente la fotografia (la rotazione è avvenuta in senso orario), si osserva che lo schermo bianco attraverso i due filtri diventa invisibile, e che la luce del raggio laser non raggiunge più lo schermo; infatti la finestra tra i due filtri ci appare assolutamente nera, cioè opaca. Se infatti lascio cadere un foglio di carta attraverso due grate le cui sbarre sono perpendicolari l'una all'altra, esso attraversa la prima, ma si ferma sulla seconda. Il paragone è semplice eppure efficace.
	Questo che vedete, approntato dal mio brillante ex studente ed ora collega Domenico Maisto, è il dispositivo per la verifica quantitativa della legge di Malus. Ruotando l'asse ottico di uno dei due filtri polarizzatori visti sopra, tramite un luxmetro si verifica effettivamente che l'intensità della luce trasmessa varia con il quadrato del coseno dell'angolo di sfasamento tra i due filtri, anche se resterà sempre un "fondo" diverso da zero, dovuto al fatto che l'esperienza non viene condotta nell'oscurità totale.
	Lo strumento visibile in questa fotografia accanto al suo astuccio d'altri tempi (è il caso di dirlo) si chiama polarimetro. Si tratta di uno strumento utilizzato per misurare l'angolo di cui ruota il piano di polarizzazione di un fascio di luce che attraversa una determinata sostanza, contenuta in una delle fialette contenute nell'astuccio. Lo strumento contiene un filtro Polaroid che lascia passare solo la luce polarizzata lungo l'asse ottico del filtro. Ruotandolo mediante la ghiera metallica visibile in figura, muta l'intensità della luce che riesce ad attraversare lo strumento e a giungere all'occhio dell'osservatore.
	Quelli qui fotografati sono gli occhiali fotocromatici dell'autore di questo sito. Come si vede, le loro lenti, una volta esposte ad intensa luce solare, si scuriscono notevolmente, ma ritornano gradualmente alla trasparenza iniziale appena la luminosità diminuisce (ad esempio in un ambiente chiuso). Il fenomeno ha un'origine fotochimica, grazie ad una reazione chimica reversibile: il vetro viene reso fotocromatico aggiungendo ad esso microcristalli di alogenuro d'argento ad oltre 600° C. Questo tipo di occhiali è molto comodo, ma non può sostituire del tutto gli occhiali da sole perchè non può scurirsi così tanto da bloccare completamente i raggi ultravioletti solari.
	Questi sono dei microscopi ottici, cioè strumenti composti da due sistemi di lenti, detti rispettivamente obiettivo ed oculare. L'obiettivo è formato da lenti a distanza focale molto piccola, che di un oggetto posto vicino al fuoco forniscono un'immagine reale ed ingrandita. L'oculare, al quale si appoggia l'occhio, è invece formato da due lenti convergenti e funziona come una normale lente di ingrandimento, fornendo un'immagine virtuale ed ulteriormente ingrandita dell'immagine reale fornita dall'obiettivo. Il preparato è posto su una lastrina di vetro detta vetrino, ed è illuminato dal basso o meno spesso di lato.
	Ed ecco il risultato dell'osservazione con un microscopio in dotazione al mio Liceo: la foto di una goccia d'acqua posta sopra un materiale nanotec idrorepellente, gentilmente concessami dalla mia collega Maria Rola. Incredibile come in un laboratorio scolastico possano essere scattate fotografie così meravigliose, non è vero?
	Qui vedete ritratti dal sottoscritto alcuni strumenti per effettuare semplici esperienze con le quali dimostrare la natura ondulatoria della propagazione luminosa. In basso si vede un puntatore laser, un comune laser elio-neon a luce rossa; subito sopra, a destra una fenditura da 0,12 mm realizzata con due lamette da barba accostate; e a sinistra, tre reticoli di diffrazione, rispettivamente da 100, 300 e 600 linee per mm.
	Certamente, rispetto all'interferometro sopra ritratto, questo apparato può apparire rudimentale, eppure consente di valutare con discreta precisione la lunghezza d'onda della luce. A destra si vede la mia mano che impugna il puntatore laser della foto precedente; il fascio luminoso attraversa la fenditura da 012 mm di cui sopra e, dopo un cammino di lunghezza misurabile...
	...va a formare questa figura di diffrazione da fenditura singola, nella quale i massimi ed i minimi si distinguono perfettamente. Basta segnare il massimo centrale ed i minimi sulla carta millimetrata per poi eseguire in modo semplice e didatticamente elegante la misura della lunghezza d'onda della luce laser, in questo caso 700 nm o 7000 Ångstrom. Grazie ad Emanuele Ferrara (III B cl. a.s. 2005/06) per la collaborazione.
	Per eseguire esperienze di interferenza dei raggi luminosi si può inserire nel dispositivo sopra descritto, anziché una fenditura, un reticolo del quale è noto il passo reticolare (di solito dell'ordine del micron), contenuto nella diapositiva bianca visibile al centro della fotografia. Al di là del reticolo si vede la morsa nella quale è stato incastrato il puntatore laser. In questo caso si ottengono più punti luminosi, di intensità variabile verso l'esterno.
	In questo caso, l'esperienza di interferenza dei raggi luminosi è stata eseguita avvicinando il laser (visibile sulla destra) al reticolo (al centro) e proiettando il fascio di luce sullo schermo nero (a destra). Le foto sottostanti, leggermente mosse perchè il laboratorio è stato oscurato onde visualizzare al meglio il fenomeno dell'interferenza, illustrano le frange di interferenza ottenute utilizzando un reticolo con 80 fenditure per millimetro (sopra) e 200 fenditure per millimetro (sotto). L'effetto è indubbiamente spettacoloso!
	La fotografia riprende la scatola di legno che contiene un'ampia collezione di reticoli, tra cui quello ritratto nella fotografia precedente, nonché un' utile guida metallica su cui sistemarli mediante un supporto a forma di cuneo. Utilizzando il laser sopra descritto è facile osservare attraverso di esso l'interferenza e la diffrazione delle onde luminose.
	La guida dell'immagine soprastante è qui sfruttata per reggere un diaframma ad apertura regolabile, simile all'otturatore delle più antiche macchine fotografiche. Tramite una levetta è possibile regolarne a piacere l'apertura, per cui, facendo passare attraverso di essa la luce di un laser, si può notare che il fenomeno di diffrazione compare solo allorché l'apertura è stretta a sufficienza.
	Anche questa fotografia la si deve a Marta Milano, e rappresenta un altro geniale dispositivo per verificare il fenomeno dell'interferenza delle onde luminose con il metodo di Young: la luce di un laser viene scomposta in due sulla destra, poi un fotodiodo (estrema sinistra) misura l'intensità della luce e la tabula direttamente su Pc. Come si vede si ottengono i massimi e minimi tipici di una figura d'interferenza, dimostrando così inequivocabilmente che la luce è un'onda.
	Anziché con il metodo di Young si può verificare l'interferenza della luce con il metodo di Fresnel: si fa riflettere la luce su due specchi leggermente inclinati l'uno rispetto all'altro, in modo che i raggi riflessi interferiscano tra loro, rappresentando due sorgenti coerenti (cioè capaci di generare onde luminose con stessa ampiezza, stessa frequenza e stessa fase).
	La dispersione della luce è illustrata in modo eccezionale da questo dipinto di Martina Pariani (5SF1 a.s. 2007/08 del Liceo Artistico Candiani di Busto Arsizio), in cui un prisma divide la luce bianca nei tradizionali "sette" colori, ed un altro ricompone la luce bianca. Si tratta di una rappresentazione artistica perchè i colori non sono sette, ma infiniti quante le frequenze...
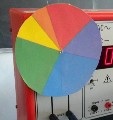
	I colori separati tra di loro possono essere riuniti tra di loro anche attraverso lo spettacoloso disco di Newton qui mostrato, un disco di carta diviso in sette settori di uguale ampiezza colorati con i sette colori dell'iride, e fatto ruotare rapidamente per mezzo di un apposito motorino la cui velocità è regolabile. Come si vede da questo breve filmato, l'occhio percepisce i colori sovrapposti tra di loro, ed il disco tende ad assumere nettamente una colorazione bianca!
	In figura si vede un semplice dispositivo sperimentale per verificare il fenomeno della dispersione della luce bianca da parte di un prisma. Allo scopo si è utilizzato un proiettore, un collimatore che permette di ottenere un fascio luminoso i cui raggi sono per lo più tutti paralleli tra di loro, un prisma di plexiglas ed uno schermo bianco sul quale, come si vede in basso nel laboratorio oscurato, si vede la successione dei colori separati tra di loro.
	La fotografia illustra tre comunissime applicazioni pratiche del fenomeno di dispersione della luce, che tutti noi possiamo osservare nelle nostre case. In basso c'è un normale compact disc, i cui mille colori sono dovuti al fatto che la luce incidente su di essa incontra i piani e delle depressioni scavate dal laser che nel disco memorizzano i bit, ed il loro alternarsi produce la formazione dell'arcobaleno. Lo stesso fenomeno è alla base dello splendido effetto ottico di una figurina dei calciatori e dell' ologramma che rende difficili da falsificare le comuni banconote da 10 euro.
	Quello illustrato in figura è uno spettroscopio, strumento presente anche nello Scaffale Virtuale di Fisica Atomica; qui però vedremo un numero maggiore di immagini che lo riguardi, perchè esso è basato sul principio della dispersione della luce. L'idea è quella di studiare la composizione di gas o altri materiali incandescenti studiando le frequenze da essi emesse dopo averle separate per mezzo di un prisma; in tal modo si studia per esempio la composizione delle stelle lontane.
	In questo caso si studia per esempio lo spettro di emissione generato da una lampadina al neon (riconoscibile per il tipico colore rossastro). Ogni atomo, se eccitato (in questo caso dal passaggio di corrente elettrica), vede i suoi elettroni saltare da un livello energetico ad uno più elevato. In seguito gli elettroni ritornano sul loro livello energetico ed emettono la differenza di energia tra i due stati sotto forma di radiazione luminosa, il che genera uno spettro a righe.
	Lo spettro a righe suddetto viene ottenuto facendo passare la luce attraverso un prisma, la cui posizione è regolabile mediante una vite senza fine. In tal modo l'oculare (visibile nella foto sottostante) "spazza" tutta l'ampiezza dello spettro e permette di studiare la distribuzione delle sue righe spettrali.
	Se invece si fa passare la luce bianca attraverso un gas o altro materiale trasparente, nel corrispondente spettro (detto di assorbimento) si nota la presenza di righe scure verticali, dovute stavolta all'assorbimento di certe frequenze da parte dei livelli energetici degli atomi. Qui lo spettro di assorbimento è stato proiettato su una foglio di carta (la mano appartiene alla prof.ssa Chiara Brivio).
	A proposito di dispersione della luce, gli astronomi dividono le stelle in sette classi spettrali a seconda della presenza delle righe di assorbimento nei loro spettri. le stelle classi sono indicate dalle lettere O, B, A, F, G, K, M (per ricordarle in ordine si utilizza la filastrocca inglese: « O, Be A Fine Girl, Kiss Me ». Il nostro Sole è del tipo spettrale G.
	Dulcis in fundo, un interferometro di Michelson-Morley. Sembra incredibile, ma è stato un apparecchio come questo a decretare il superamento della Fisica Classica! Infatti con il suo ausilio, tra il 1887 e il 1906, Michelson e Morley tentarono di misurare la velocità relativa della Terra rispetto all'ipotetico etere: la velocità della luce dovrebbe essere minima quando viaggia nella stessa direzione e verso della Terra, e massima nel caso opposto. L'esperimento si basa sull'interferenza della luce; ruotando l'interferometro di 180°, tuttavia, Michelson scoprì che le frange di interferenza non si spostano affatto, come invece sarebbe dovuto accadere. Dunque l'etere non esiste e la luce non segue la composizione galileiana delle velocità. Nel 1905 l'interpretazione di quest'esperienza portò Einstein alla formulazione della Teoria della Relatività Ristretta.
Cliccate qui per scaricare alcune schede per realizzare molte delle esperienze di questa galleria
Queste immagini possono essere liberamente utilizzate da chiunque, purché se ne citi la fonte

Torna alla galleria immagini del mio sito