Galleria di immagini: Matematica

	In questa galleria presenterò, in ordine alfabetico, tutta una serie di immagini di curve e di figure che si incontrano nello studio della matematica. Cominciamo con l'algebra. L'alunno Nicola Tonetti (II B cl. a.s. 2005/2006) ha ripreso un esempio bellissimo di come si possa realizzare efficaci supporti didattici anche con del materiale povero. E' bastato il cartone di un normale rotolo di carta da cucina, oltre a quattro strisce di carta fissate su di esso in modo da esse libere di rotargli attorno, per fabbricare un abaco binario, il quale consente di illustrare la formazione dei numeri binari successivi da 0 fino a 1111, corrispondenti ai numeri decimali da 0 a 15. Che ne dite?
	Una leggenda racconta che il Gran Visir di uno Shah di Persia particolarmente guerrafondaio inventò per il suo signore il gioco degli scacchi, che rappresenta una guerra (incruenta) in miniatura. Come compenso per la sua invenzione il Gran Visir chiese un chicco di grano sulla prima casella, 2 sulla seconda, 4 sulla terza, 8 sulla quarta, e così via fino alla sessantaquattresima. Il numero totale di chicchi che egli aveva chiesto è immenso: si tratta della somma dei primi 64 termini di una progressione geometrica di ragione 2, somma pari a 2⁶⁴ – 1, cioè 1.85 x 10¹⁹: 18 miliardi di miliardi! Questo fatto viene ricordato anche da Dante in Paradiso XXVIII, 92-93: « ed eran tante, che 'l numero loro / più che 'l doppiar de li scacchi s'inmilla »!
	In questa foto digitale è rappresentato il regolo calcolatore di mio padre. Per quanto possa parere strano a noi, abituati alle calcolatrici elettroniche, sfruttando abilmente le proprietà dei logaritmi, questo semplicissimo apparecchio può calcolare in modo rapido ed efficiente prodotti, rapporti, potenze e radici anche di numeri molto grandi!
	Questa suggestiva immagine rappresenta un lavoro della studentessa Martina Silvestri, dedicato al tema dell'infinito. Il simbolo matematico di infinito venne utilizzato per la prima volta da John Wallis nel 1655, e probabilmente deriva da una rielaborazione della lettera M, che nel sistema di numerazione romano indicava 1000, e quindi un numero grandissimo; ma Wallis lo scelse anche perché il doppio occhiello di questo simbolo può essere percorso all'infinito. Inoltre esso ricorda molto l'anello di Moëbius, di cui parleremo più sotto.
	Passiamo alla geometria piana. Ricordo che quando ero bambino mi ero fabbricato con legno, chiodi e martello uno strumento chiamato geopiano (questa è una versione più recente): tendendo un elastico tra i chiodi è possibile realizzare praticamente qualsiasi figura piana a lati rettilinei. Per spiegare la geometria ai bambini è l'ideale!
	Questa foto, scattata a Venaria (TO) nel gennaio 2006 dall'amico ingegnere Sandro Degiani, dimostra nel modo più semplice come anche le parallele si incontrano in un punto. Naturalmente si tratta di un... punto di fuga, cioè di un punto all'infinito, che noi identifichiamo con la direzione delle rette parallele. Il fenomeno della prospettiva ci permette di vedere le rette parallele concorrere in questo punto all'infinito. La scoperta delle regole della prospettiva rivoluzionò le arti grafiche a cavallo tra il quattrocento e il cinquecento.
	Qui vedete ritratto uno dei lavori realizzati dagli studenti del mio Liceo, che dimostra in tre dimensioni il significato delle proiezioni ortogonali e delle sezioni di solidi, realizzate in disegno tecnico ed evidenziate tramite parti tratteggiate. Il piano di sezione è qui realizzato mediante un piano di plexiglas, mentre il solido (in questo caso una piramide) è materialmente realizzato mediante carta ritagliata e incollata. I miei complimenti agli autori!
	A proposito di prospettiva, ecco a voi, disegnato da Ilaria Veronese, il cosiddetto triangolo di Penrose, che può esistere solamente come rappresentazione bidimensionale e non può essere costruito nello spazio, poiché presenta una sovrapposizione impossibile di linee con differenti costruzioni prospettiche. Appare come un solido costituito da tre prismi uniti tra loro con tre angoli retti a formare un triangolo, ma in geometria euclidea la somma degli angoli interni di un triangolo non può essere superiore a 180° e quindi non può esserci più di un angolo retto.
	Questo "triangolo impossibile" fu ideato dall'artista svedese Oskar Reutersvärd (1915-2002) nel 1934 e reso popolare nel 1958 dal matematico inglese Roger Penrose (1931-), che lo definì « l'impossibile nella sua forma pura ». In realtà, come si vede in questa foto, il triangolo di Penrose può essere realizzato in pratica grazie a un ingegnoso gioco prospettico, con tre aste colorate e disposte a 90° l'una dall'altra: ponendosi in un punto particolare dello spazio, è possibile "vedere" il triangolo come realmente esistente. L'incredibile modellino è stato realizzato da Jacopo Piccoli, studente del mio Liceo.
	Anche il logo della Renault, adottato nel 1972, è un quadrilatero di Penrose, come vi potete rendere conto osservando la foto a fiamco, scattata nel parcheggio del mio Liceo. Era inevitabile che anche il marketing attingesse a piene mani da queste "figure geometriche impossibili" per attirare l'occhio dei potenziali avventori.
	Ed ecco un'altra incredibile figura geometrica impossibile, ma realizzata in pratica con un gioco prospettico. La foto mi è stata spedita dall'amica ingegnere Giulia Grazi Bracci, della quale non conosco i credits (se qualcuno li conosce, me li segnali). Appare evidente l'impossibilità di realizzare in pratica una figura come questa, che viola ogni regola del buon senso, ma che dimostra altresì come l'occhio (o meglio il cervello) umano possa essere facilmente ingannato dalla prospettiva. Quest'immagine fa il paio con alcune illusioni ottiche presentate nell'Armadio Virtuale dedicato alle onde!
	Non poteva mancare in questa galleria un origami. Esso mi è stato regalato dal mio studente Vittorio Gallivanone (5 A a.s. 2017/18) e rappresenta, come si vede, il modello della molecola di DNA, realizzata senza usare né forbici né colla. Vittorio ha dedicato la sua tesina di Esame di Stato proprio agli origami, ha portato alcuni esemplari da lui realizzati, e alla fine dell'esame orale me ne ha regalato uno. Grazie mille!
	Ed ecco altri origami, di differenti dimensioni, realizzati stavolta dal mio studente Federico Sottocorno (5 H a.s. 2021/22). Il termine origami ((折り紙) deriva dal giapponese "oru", "piegare", e "kami", "carta". In questo caso si parla in particolare di orizuru (折鶴), "gru piegata", da "ori", "piegato" e "tsuru", "gru": èl a forma considerata più classica tra tutti gli origami giapponesi. Si tratta di una rappresentazione stilizzata della gru della Manciuria, che ha un significato speciale nella cultura giapponese, in cui si ritiene possa vivere fino a mille anni. È spesso usata come un simbolo cerimoniale o per la decorazione dei tavoli dei ristoranti, e su di essa sono stati condotti importanti studi di topologia!
	La foto che vedete qui a sinistra me la ha inviata il compianto amico e collega Giovanni Uristani che, con la famiglia, ha partecipato ad una vacanza nelle isole del Mar Egeo e, tra le altre, non poteva certo evitare di toccare Samo, a poca distanza dalla costa dell'attuale Turchia, nota nell'antichità per la squisita produzione di vasi (ancor oggi si dice "portare vasi a Samo" come sinonimo di un'operazione assolutamente inutile), e soprattutto per essere la patria del filosofo Pitagora, al cui nome è legato l'omonimo teorema, in realtà assai più antico di lui. Grazie a Giovanni per averci inviato la foto del monumento dedicato a Pitagora sull'isola che gli ha dato i natali!
	Cosa sarà mai ciò che è ritratto in questa foto? Si tratta di un tabellone di legno che può essere usato per dimostrare il teorema di Pitagora, secondo il quale la somma delle aree dei quadrati costruiti sui cateti è pari all'area del quadrato costruito sull'ipotenusa. Come si vede, si vuole usare il metodo dell'equiscomponibilità: il triangolo blu va posto al centro, mentre le cinque parti poligonali possono essere usate per ricostruire sia i due quadrati costruiti sui cateti, sia quello costruito sull'ipotenusa!
	Non ci credete? Ecco la mia soluzione. Per identificare le cinque parti poligonali sono stati usati altrettanti numeri! E' stato dimostrato che l'equiscomponibilità del quadrato costruito sull'ipotenusa e dei due quadrati costruiti sui cateti può essere verificata in infiniti modi, come dimostrano questo file e questo video: provare per credere!!
	In questa figura, costruita con Cabri-Geomètre II come molte altre immagini di questa carrellata, vediamo la classificazione degli angoli formati da due rette parallele e tagliati da una trasversale, classificazione che tutti abbiamo studiato a scuola. Con Cabri-Geométre II, che io uso spesso per le mie classi, è possibile verificare la congruenza degli angoli alterni interni, alterni esterni e corrispondenti, e la supplementarietà degli angoli coniugati. Proprio nella possibilità di verificare facilmente i teoremi di geometria sta l'utilità dell'uso di questo programma interattivo.
	In questa figura è stato rappresentato il famosissimo teorema di Talete: se due rette trasversali tagliano un fascio di rette parallele, a segmenti congruenti staccati sulla prima trasversale corrispondono segmenti congruenti sulla seconda, e le due famiglie di segmenti staccate sulle due rette sono direttamente proporzionali tra di loro. Qui se ne vede la verifica eseguita con Cabri-Geomètre II.
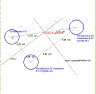
	In questa figura è rappresentata la proprietà secondo cui una simmetria centrale è ottenibile come prodotto di due simmetrie assiali che hanno gli assi tra di loro paralleli.
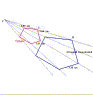
	Ecco la rappresentazione geometrica, ottenuta con Cabri-Geomètre II, di una omotetia. Preso un punto C detto centro di omotetia ed un numero k detto rapporto di omotetia, essa fa corrispondere ad ogni punto P un punto P' tale che O, P e P' sono allineati tra loro, e che OP' = k OP. Se k > 0 l'omotetia si dice diretta, se k < 0 si dice inversa. Se k = 1 si ha un'identità, se k = – 1 si ha una simmetria centrale. Essa conserva il parallelismo ed il prodotto di due omotetie è un'omotetia il cui rapporto è pari al prodotto delle omotetie fattori.
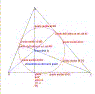
	Il teorema di Feuerbach dice che in un triangolo qualsiasi i punti medi dei tre lati, i piedi delle tre altezze e i punti medi dei tre segmenti che congiungono l'ortocentro con i tre vertici individuano una sola circonferenza, la quale si dice circonferenza dei nove punti o circonferenza di Feuerbach. Un'interessante curiosità geometrica, nevvero?
	Oltre alle circonferenze inscritte e circoscritte ad un triangolo qualunque esistono anche le circonferenze exinscritte. Sono le circonferenze tangenti ad un lato del triangolo e ai prolungamenti degli altri due. I centri delle circonferenze exinscritte si dicono excentri, e si trovano all'intersezione tra la bisettrice di un angolo interno al triangolo e le bisettrici degli angoli esterni agli altri due. Ogni triangolo possiede tre excentri ad esso esterni.
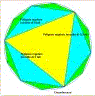
	Si dice poligono regolare un poligono che ha tutti i lati e tutti gli angoli tra loro congruenti. I poligoni regolari sono infiniti e sono tutti inscrittibili (e circoscrittibili) in una circonferenza. Considerando un triangolo equilatero inscritto in una circonferenza e dimezzando gli archi delimitati dai suoi lati si ha un esagono regolare; ripetendo l'operazione si ha un dodecagono regolare; e così via. Come mostra questa immagine, la successione delle aree dei poligoni regolari ottenuti per successivi dimezzamenti tende all'area del cerchio; questo metodo può essere utilizzato per trovare valori approssimati di pi greco.
	Le connessioni fra geometria ed arte sono tante e tali, che per trattare di esse non ci vorrebbe un Armadio Virtuale ma una enciclopedia. Un esempio molto bello di tale connessione è rappresentata dal Castel del Monte, in provincia di Bari, definito da alcuni il più bel castello d'Europa, fatto edificare dall'imperatore Federico II nel 1240: esso ha pianta ottagonale ed anche gli otto torrioni sono ottagonali (le congetture su di un significato magico di queste forme appartengono al campo della fantasia). Il modellino si trova nella Biblioteca del mio liceo ed è stato costruito dagli allievi durante le lezioni di arte. Bravi!
	Ed ecco un altro esempio della suddetta connessione. Questo è l'arco di Costantino, fatto edificare dall'omonimo imperatore per celebrare la sua vittoria su Massenzio, e se si trova in questa galleria è perchè la sua altezza è pari alla sezione aurea della larghezza. Si dice sezione aurea di un segmento la sua parte che risulta media proporzionale tra l'intero segmento e la parte rimanente. Nell'antichità si pensava che la Natura fosse stata creata usandola come metro, e l'arte ne risente!
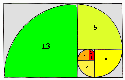
	Quella in figura è la spirale di Fibonacci, cioè una spirale costruita accostando quadrati i cui lati crescono seguendo la successione di Fibonacci, in cui ogni elemento è ottenuto sommando i due precedenti a partire da due 1 (si ha così 1, 1, 2, 3, 5, 8, 13, 21...); essa descrive il normale accrescimento di popolazioni di esseri viventi. Questa spirale è molto vicina alla spirale aurea, costruita con rettangoli aurei successivi (il rettangolo aureo ha i lati in proporzione pari alla sezione aurea).
	Cosa ci fa in questo Armadio Virtuale, e non in quello di Zoologia, mi chiederete voi, questa magnifica conchiglia di Nautilus (un mollusco cefalopode), che misura più di 20 cm, fotografata al Civico Museo di Storia Naturale di Milano? Il fatto è che questo mollusco dei mari tropicali, considerato un fossile vivente perchè un esemplare vivo è stato pescato solo nel 1829, ha la conchiglia che cresce secondo una perfetta spirale aurea, come quella descritta subito sopra. Davvero la sezione aurea sembra farla da padrone in natura: ora capite perchè essa fu chiamata anche "divina proporzione"!
	Questi modelli del Partenone di Atene (l'uno come appare oggi, l'altro una ricostruzione del suo aspetto originale) sono stati realizzati dagli studenti Alessia Messuti, Giulia Randelli e Jacopo Piccoli, e vogliono dimostrare come anche la facciata di uno dei più celebri monumenti sacri di tutti i tempi sia stata progettata in modo da essere inscritta in un rettangolo aureo. Infatti il modellino più piccolo mostra una spirale di Fibonacci inscritta nella facciata! Si noti che se prendo un rettangolo aureo e gli sotraggo il quadrato costruito sul lato più corto, ciò che resta è un altro rettangolo aureo!
	L'insolita foto, di una penna lanciata su di un parquet, illustra la ripetizione del ragionamento seguito da Georges-Louis Leclerc, conte di Buffon (1707-1788), per il calcolo sperimentale di pi greco. Siccome a sua moglie spesso cadeva sul parquet l'ago con cui cuciva, egli pensò di calcolare la probabilità che l'ago intersecasse le righe del parquet. Se L è la lunghezza dell'ago, la probabilità risultò pari a L/2π. Ripetendo la prova un grandissimo numero di volte, il rapporto tra le volte che l'ago copre una linea ed il numero totale dei lanci tende a questo rapporto, ed è dunque possibile calcolare un valore approssimato di pi greco!
	Quest'immagine è il risultato della composizione di più foto digitali da me scattate il 18/7/2007. e mostra come Piazza San Pietro a Roma abbia la forma di un ovale. Tale figura è ottenuta unendo quattro archi di circonferenza, e i due di raggio più piccolo sono chiaramente segnati sulla pavimentazione (foto in basso a sinistra). Ponendosi in uno di essi, si vedranno le due file di colonne perfettamente sovrapposte (foto in alto), mentre in qualunque altro punto della piazza ciò non avverrà (foto in basso a destra). L'arte al servizio della Matematica...
	Si dice lunula la figura piana limitata da due archi di circonferenza. Leonardo da Vinci (1452-1519) dimostrò che esistono lunule equivalenti a figure limitate da segmenti di retta, e la cui area è quindi esprimibile medianti numeri non trascendenti, a differenza dell'intero cerchio. Questo ne è un esempio da lui stesso segnalato: preso un triangolo rettangolo isoscele, si traccia la semicirconferenza che ha per diametro l'ipotenusa ed il quarto di cerchio che ha il lato come raggio ed il vertice dell'angolo retto come centro. I due archi delimitano una lunula equivalente al triangolo (vedi anche più sopra).
	Ed ecco il teorema di Alhazen (matematico arabo, vero nome Abu Alì al-Hasan ibn al-Haitham, circa 965-1039): se sui due cateti di un triangolo rettangolo si costruiscono due semicirconferenze, la somma delle lunule (vedi foto precedente) comprese fra queste e la semicirconferenza costruita sull'ipotenusa nel semipiano del triangolo, è equivalente al triangolo rettangolo stesso.
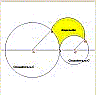
	La dropenoide è un triangolo a lati circolari costruito come si vede in figura: prese due circonferenze tangenti esternamente in A, si considerano due loro raggi tra di loro paralleli OB ed O'B' e si costruisce la semicirconferenza di diametro BB' nel semipiano che non contiene A. Gli archi AB, BB' ed AB' delimitano la dropenoide (in giallo).
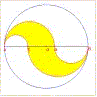
	La figura in giallo qui rappresentata è nota come pelecoide. La si ottiene prendendo due punti C e D sul diametro AB di una circonferenza qualunque e costruendo in uno dei due semicerchi così ottenuti le semicirconferenze di diametri AC e AD, e nell'altro le semicirconferenze di diametri CB e DB. Le quattro semicirconferenze così ottenute delimitano la pelecoide.
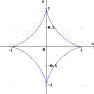
	Cominciamo ora una lunga galleria di linee piane disegnate con un apposito programma, procedendo in ordine alfabetico. L'asteroide è una linea piana di equazione cartesiana x^(2/3) + y^(2/3) = a^(2/3). È la prima linea piana che incontriamo in questa carrellata. Il suo grafico è stato ottenuto mediante Derive 5, come la maggior parte delle linee di questa galleria.
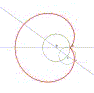
	La cardioide è una linea piana di equazione cartesiana (x² + y²)² – 4 a x (x² + y² – 4 a² y²) = 0. Per costruirla si consideri una circonferenza di centro O, un suo punto Q ed una retta r qualunque uscente dal suo centro. Detta C l'intersezione tra r e la circonferenza, si costruisca l'ulteriore circonferenza che ha centro in C e passa per Q. L'intersezione tra r e questa seconda circonferenza che si trova al di là di C genera la cardioide al ruotare di s attorno al centro O.
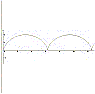
	La cicloide è una linea piana di equazioni parametriche x = R (t – t sen t) ed y = R (1 – cos t). Questa curva può essere ottenuta come il luogo descritto dal punto di una circonferenza che rotola senza strisciare su di una linea retta. La cicloide è detta anche brachistocrona perchè, tra tutte le curve che congiungono due punti a quota diversa, è quella lungo la quale un grave scivola dall'uno all'altro nel tempo più breve, come dimostrò Giacomo Bernoulli nel 1696.
	La cissoide di Diocle è una linea piana di equazione cartesiana x (x² + y²) – a y² = 0. Per costruirla si consideri una circonferenza, il suo diametro AB e la tangente r in B alla circonferenza. Fatta uscire da A una retta qualunque s, essa intersechi la circonferenza in C e la retta r in D. Si prenda poi su s un punto P tale che AP = CD. Il luogo dei punti P al variare di s descrive la cissoide, curva che permette un'elegante rettificazione della circonferenza.
	La concoide di Nicomede è una linea piana di equazione cartesiana (x – b)² (x² + y²) – a² y² = 0. In generale si dice concoide di una curva rispetto ad un punto A il luogo dei punti P appartenenti ad una retta r uscente da A, tali che il segmento da essi individuato abbia misura costante 2 a e che il punto medio di tale segmento coincida con l'intersezione tra la curva data e la retta r. La concoide di Nicomede è la concoide di una retta.
	La catenaria è una linea piana di equazione cartesiana y = (e^x +e^–x )/2. Tale funzione prende il nome di coseno iperbolico, e la catenaria rappresenta la linea determinata da una catena o da una fune vincolata agli estremi e sottoposta solo al proprio peso, come ci dimostra la fotografia successiva.
	Questa fotografia, messa gentilmente a disposizione dalla collega Claudia Bina, illustra il fenomeno fisico cui si accennava a proposito della curva precedente: se una catena, o filo, o fila di perline è sottoposta unicamente al proprio peso, si dispone lungo una curva chiamata catenaria, descritta dalla funzione coseno iperbolico. I molti fili che compongono questa piccola opera d'arte moderna si dispongono tutti secondo altrettante catenarie, ma chiunque di noi può rendersene conto facilmente, osservando i cavi dell'alta tensione tesi tra due tralicci successivi...
	La cubica è una linea piana di equazione cartesiana y = a x³ +b x² + c x + d, con a, b, c, d parametri reali. Essa ha al massimo tre intersezioni con l'asse delle ascisse, due estremi relativi (un massimo e un minimo) ed un flesso.
	La curva k è la linea piana definita come luogo dei punti di tangenza di due rette uscenti dall'origine con una circonferenza di raggio fisso e centro sull'asse x, al variare dell'ascissa di questo centro. È simmetrica rispetto all'asse y.
	La foto, scattata dal sottoscritto (cui appartiene anche il dito), illustra in maniera chiara come si può disegnare un'ellisse con il cosiddetto "metodo del giardiniere". Si dice ellisse il luogo dei punti che hanno costante la somma delle distanze da due punti fissi detti fuochi. Basta allora fissare due chiodini nei fuochi, tendere una corda tra di essi e far scorrere la matita tutt'intorno; l'ellisse verrà disegnata in maniera assolutamente naturale. La somma costante delle distanze tra i fuochi è pari al cosiddetto "asse maggiore". Se i due fuochi coincidono, l'ellisse diventa una circonferenza.
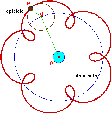
	L'epicicloide è il luogo descritto dal punto P di una circonferenza detta epiciclo che ruota di moto uniforme, mentre il suo centro ruota di moto uniforme su un'altra circonferenza detta deferente. Questa curva rappresenta il moto dei pianeti attorno alla Terra nel modello tolemaico, che infatti è detto modello ad epicicli (vedi l'Armadio Virtuale di Geografia Astronomica).
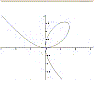
	Si dice folium di Cartesio la linea piana di equazione cartesiana x³ + y³ – 3 a x y = 0. Essa è simmetrica rispetto alla bisettrice del primo e terzo quadrante, essendo invariante rispetto allo scambio tra loro di x e y, ed è dotata di un punto doppio nodale, perchè il termine di grado minimo è di secondo grado (xy). Uguagliando a zero questo termine si hanno le due tangenti nodali, che coincidono con i due assi cartesiani.
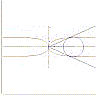
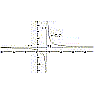
	La funzione omografica è una linea piana di equazione cartesiana y = (a x + b)/(c x + d). Il suo nome deriva dal fatto che questa è anche l'equazione di una trasformazione chiamata omografia. Si tratta di una iperbole equilatera con gli assi paralleli agli assi cartesiani ed avente centro nel punto (– a/c ; d/c ) .
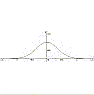
	La curva di Gauss o gaussiana è una linea piana di equazione cartesiana 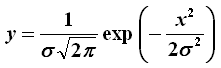, dove σ è detto scarto quadratico medio. Essa esprime la distribuzione degli errori commessi nelle misure di una certa grandezza.
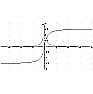
	Ed ecco a voi i grafici della funzione y = 1/(1+x²) e del suo integrale indefinito y = arc tg x, ottenuti mediante Derive 5 e disegnati sul medesimo grafico, per dimostrare che dove si annulla la seconda, la prima ha un massimo, a riprova del teorema di Torricelli-Barrow secondo cui la derivata della primitiva di una funzione coincide con la funzione stessa.
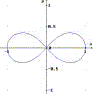
	La lemniscata di Bernoulli è una linea piana di equazione cartesiana (x² + y²)² – a (x² – y²) = 0. Il suo nome deriva da lemnisco, " palma"; si tratta del luogo dei punti di un piano per i quali il prodotto delle distanze da due punti fissi F', F è costante ed uguale al quadrato della semidistanza dei due punti; è una quartica razionale con un punto doppio nodale, come conferma il fatto che i termini di secondo grado, se uguagliati a zero, danno y = ± x, le due tangenti nel punto doppio.
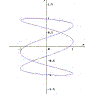
	Le curve di Lissajous sono linee piane di equazioni parametriche x = a sen (nt + c), y = b sen (mt + d). Rivestono notevole importanza in fisica, poiché descrivono l'interferenza di due moti oscillatori perpendicolari di frequenze diverse tra di loro e con una determinata differenza di fase. Se quest'ultima è pari a 90°, per frequenze tra loro uguali la figura di Lissajous è una circonferenza. In figura la differenza di fase è di 45° ed il rapporto tra le due frequenze è pari ad 1/3.
	La lumaca di Pascal ha equazione cartesiana (x² + y²– 2 a x)² – b² (x² + y²) = 0 ed è la concoide della circonferenza (vedi sopra). Faccio notare che il Pascal che le ha dato il nome non è Blaise ma suo padre Etienne.
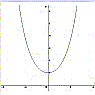
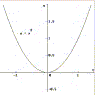
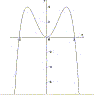
	La parabola è una linea piana di equazione cartesiana y = a x² +b x + c, con a, b, c parametri reali. Essa ha al massimo due intersezioni con l'asse delle ascisse, un estremo relativo (un massimo se a < 0 oppure un minimo se a > 0) ed è priva di flessi. Essa è definita anche come il luogo dei punti equidistanti da un punto fisso detto fuoco e da una retta fissa detta direttrice.
	Quella illustrata in figura è un'antenna parabolica. Cosa ci fa in questo Armadio Virtuale? Semplice: essa illustra una proprietà fondamentale della parabola, secondo cui la normale ad essa in ogni punto (cioè la perpendicolare alla tangente) è bisettrice dell'angolo formato dalla congiungente quel punto con il fuoco della parabola e dalla retta per quel punto parallela all'asse. Ciò significa che un raggio proveniente dall'infinito che si riflette su di uno specchio parabolico va a convergere sempre esattamente nel fuoco. Tale proprietà è sfruttata appunto nelle antenne paraboliche, dove le onde radio provenienti dal satellite e pressoché tra di loro parallele vanno a convergere tutte nel ricevitore. Ingegnoso, no?
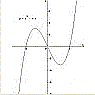
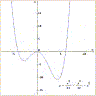
	La quartica è una linea piana di equazione cartesiana y = a x⁴ +b x³ + c x² + d x + e, con a, b, c, d, e parametri reali. Essa ha al massimo quattro intersezioni con l'asse delle ascisse, tre estremi relativi (due massimi e un minimo oppure due minimi e un massimo) e due flessi, uno ascendente e uno discendente.
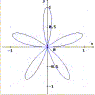
	La rodonea è una linea piana di equazione polare r = a sen (k α) oppure y = a cos (k α). Se k è un numero intero essa ha k "petali" o 2k "petali" (in figura se ne hanno cinque), a seconda che k sia pari o dispari. Se k è un numero irrazionale la rodonea ha infiniti "petali". Bella, eh? È un esempio di quella che io chiamo "matematic-art"!
	Il seno iperbolico è la funzione y = (e^x – e^–x )/2, di cui qui si vede la rappresentazione cartesiana Il seno iperbolico e il coseno iperbolico costituiscono le funzioni iperboliche, in analogia alle funzioni circolari (seno e coseno).
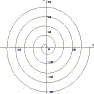
	La spirale di Archimede è una linea piana di equazione polare r = k α. Pur essendo una delle curve più conosciute anche a livello intuitivo, essa ha una rappresentazione cartesiana difficilissima.
	Potete crederci o meno, ma anche una comunissima ragnatela, come questa che vedete fotografata sull'ingresso di casa mia nel giugno 2021, non rappresenta altro che un'approssimazione della spirale di Archimede! Tale figura geometrica risponde infatti perfettamente alle esigenze dei ragni: l’uguale distanza tra i bracci della spirale fa sì che i ragni ricoprano il più fittamente possibile lo spazio presente tra i raggi della ragnatela, rendendola adatta a trattenere piccoli insetti volanti!
	La strofoide è invece una linea piana di equazione cartesiana x² (a – x) – y² (a + x) = 0. Essa è pari e priva di punti doppi, come si inferisce dal fatto che i termini di grado minimo sono di primo grado.
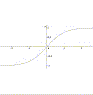
	La tangente iperbolica è la funzione y = (e^x – e^–x )/(e^x + e^–x ), di cui qui si vede la rappresentazione cartesiana È così chiamata perchè si ottiene come rapporto tra il seno iperbolico ed il coseno iperbolico. Le figure mostrano chiaramente come le funzioni iperboliche, a differenza di quelle circolari, nel campo reale non siano periodiche. Lo diventano però nel campo complesso.
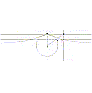
	Tocca alla cosiddetta versiera di Agnesi, di equazione cartesiana (a² + x²) y = a³. Il suo nome deriva da quello della grande matematica italiana milanese Maria Gaetana Agnesi (1718-1799) che la studiò in un suo trattato del 1748. Per disegnarla si consideri una circonferenza ed un suo punto M; si tracci la tangente t in M e si faccia uscire dal centro della circonferenza una semiretta r che interseca la circonferenza in Q e la retta t in N. Da Q si traccia la parallela a t e da N la perpendicolare a t, e queste due rette si incontrano in P. Al variare della semiretta r il punto P descrive la versiera di Agnesi.
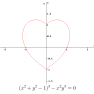
	Chiudiamo con la linea di equazione (x² + y² – 1)³ – x² y³ = 0, una curva di sesto grado pari e senza punti doppi, che non avrebbe nulla di speciale, se non fosse... perchè ha la forma di un cuore! Che l'abbia scoperta un matematico innamorato il giorno di San Valentino?
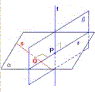
	Spostiamoci ora nell'ambito della geometria solida. In questa figura si vede illustrato il cosiddetto teorema delle tre perpendicolari: se dal piede di una perpendicolare ad un piano si traccia la perpendicolare ad una retta di questo piano, quest'ultima è perpendicolare al piano individuato dalle prime due rette. Gli studenti sono normalmente nemicissimi di questi teoremi, giacché li devono studiare a memoria...
	Al confine tra geometria piana e solida ci sono i cosiddetti libri popup: sono dei normali libri dai quali, quando vengono aperti, scaturiscono figure solide, in precedenza perfettamente ripiegate tra le loro pagine, che rappresentano persone o animali o paesaggi. Nella foto composita qui a sinistra potete vedere un libro popup realizzato dagli studenti della 3 E a.s. 2009/10 del mio Liceo in occasione di una mostra dedicata al bicentenario della nascita di Charles Darwin: infatti dalle pagine del libro salta su proprio la figura del fondatore della moderna teoria evoluzionistica!!
	Un gioco molto divertente è quello di costruire solidi di cartone mediante carta. Non si tratta affatto di un passatempo per infanti, poiché richiede di conoscere perfettamente lo sviluppo sul piano delle principali figure solide. Per un cubo per esempio occorrono sei quadrati, quattro dei quali uno in fila all'altro ed uniti per un lato, e i due rimanenti posti da parti opposte rispetto ad uno di essi. Ma l'esercizio più difficile consiste nel costruire figure circolari come il cono o il cilindro!
	Non è solo con la carta che gli uomini si sono divertiti a costruire modellini di solidi. Se infatti volete vedere un "modellino" (sic!) di tronco di piramide, vi basterà dare un'occhiata alla piramide di Kukulkan (nota anche come "El Castillo") che l'amico Sandro Degiani ha fotografato nel marzo 2008 a Chichén Itzá, forse la più famosa delle città Maya, nel nord della penisola dello Yucatan. Per essere un modellino, è davvero imponente!!!
	Questo curioso meme mi è stato inviato dalla collega Veronica Ventola, ed in esso le piramidi sono usate per spiegare la differenza tra somma di Riemann ed integrale. Infatti la piramide di Djoser (III dinastia, 2700 a.C.) ha solo cinque gradoni ed approssima solo grossolanamente il volume di una vera piramide. Invece la piramide di Cheope (VI dinastia, 2450 a.C.) la approssima molto meglio e quindi si avvicina all'integrale che esprime il volume dell'intera piramide. Osservandola bene da vicino però si scoprirà che anch'essa è solo una somma di Riemann, essendo formata da 210 strati di pietre! Del resto, neppure degli strati di granelli di sabbia esaurirebbe tutto il volume: l'integrale è il limite di una somma di Riemann con il numero degli addendi che va ad infinito.
	I meme di argomento matematico sono spassosissimi. Questo mi è stato spedito dall'ex studente ed ora collega Domenico Maisto, ed illustra – utilizzando Tom e Jerry come guest stars – la differenza tra integrale indefinito (sopra) e definito (sotto). Il primo infatti necessita della costante additiva C, poiché ogni funzione ha infinite primitive, che differiscono per una costante additiva (e ciò è simboleggiato dall'alleanza tra i due rivali dei cartoni animati), mentre il secondo, esprimendo l'area di una superficie in modo univoco, non ne ha affatto bisogno, come dimostra il fatto che Jerry le dice addio!
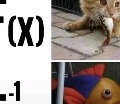	Ancora più ingegnoso è questo meme, sempre fattomi avere dall'amico Domenico. In esso il concetto di funzione inversa è rappresentato con un'efficacissima metafora visiva. Se infatti F(x) corrisponde al gatto che ingoia un pesce, la funzione inversa F^–1(x) deve giocoforza corrispondere al pesce che ingoia un gatto. Infatti, se la funzione F(x) è la relazione che fa corrispondere ad un valore di x uno ed un solo valore di y, la sua inversa F^–1(x) deve far corrispondere a quel valore di y uno ed un solo valore di x. Semplicemente geniale, voi non trovate?
	Perchè l'ellisse, la circonferenza, la parabola e l'iperbole vengono definite sezioni coniche? Perchè esse si ottengono sezionando un cono con piani di diversa inclinazione. Questo modellino in legno è utilissimo per spiegarlo agli studenti: il cono è stato segato lungo un piano inclinato e, come si vede, la sezione dà proprio vita ad una ellisse!
	La foto illustra in modo semplice ed intuitivo, come chiunque può verificare in casa propria, perchè la parabola rientra nella categoria delle sezioni coniche. In figura si vede una normale abat-jour da camera in vetro, dotata di un'apertura circolare superiore. Essa proietta un fascio di luce perfettamente conico sulla parete. L'immagine che si forma sulla parete ha la forma di una parabola, perchè la lampada è appoggiata in piano e quindi l'asse del cono di luce da essa proiettato è perfettamente parallelo alla parete. Ne segue che l'immagine che si vede risulta dall'intersezione del cono di luce con un piano parallelo al suo asse, e dunque la figura suddetta non può che essere una parabola.
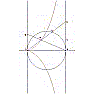
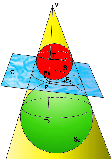
	In questo disegno è possibile vedere illustrato il cosiddetto teorema di Dandelin: tagliando una superficie conica indefinita con un piano p si ottiene una sezione a forma di ellisse; i fuochi dell'ellisse sono i punti di tangenza con il piano delle due sfere inscritte in ciascuna delle due zone di spazio in cui il cono è tagliato dal piano p, e tangenti al piano. Se il piano è perpendicolare all'asse del cono si ha una circonferenza ed i fuochi coincidono nel suo centro. Se il piano è parallelo ad una generatrice del cono si ha una parabola ed il fuoco è uno solo (l'altro va all'infinito). Se il piano è ancora più inclinato si ha un'iperbole, i cui fuochi coincidono con i punti di tangenza con esso delle sfere tangenti internamente alla superficie conica. Se il piano è parallelo all'asse del cono si ha un'iperbole equilatera.
	Si dicono poliedri archimedei quelli le cui facce sono poligoni regolari, ma non necessariamente dello stesso tipo (mentre i poliedri platonici hanno tutte le facce uguali). Eccone tre begli esempi costruiti con quadrati e triangoli equilateri. Anche il pallone da calcio è quindi un poliedro archimedeo!
	Il solido qui illustrato ha 32 facce, di cui 20 esagoni regolari e 12 pentagoni regolari. Solo una curiosità geometrica? No, perchè è sulla base di questo solido che è stato costruito il normale pallone da calcio! Come detto sopra, si tratta di un poliedro archimedeo. Ricordiamo anche che che s, f e v sono i numeri rispettivamente degli spigoli, delle facce e dei vertici di un poliedro, tra di essi vale la relazione di Eulero : s = f + v – 2.
	Ed ecco, costruiti con sferette d'acciaio ed asticelle magnetizzate, tre poliedri platonici: sono così detti i poliedri le cui facce sono poligoni regolari tutti uguali tra di loro. Anche tutti gli angoli solidi sono tra loro congruenti. Da sinistra vediamo il tetraedro regolare, il cubo o esaedro regolare e l'ottaedro regolare (gli altri sono il dodecaedro regolare e l'icosaedro regolare). Il tetraedro ha 4 facce, 6 spigoli e 4 vertici; il cubo ha 6 facce, 12 spigoli e 8 vertici; l'ottaedro ha 8 facce, 12 spigoli e 6 vertici.
	Ecco invece un dodecaedro regolare, il quarto dei cinque solidi platonici, che ha 12 facce, 20 vertici e 30 spigoli; le facce sono pentagoni regolari. Nella sua famosissima "Ultima Cena" del 1955, oggi alla National Gallery of Art di Washington, il pittore catalano Salvador Dalí (1904-1989) inscrisse l'istituzione del Santissimo Sacramento proprio dentro un dodecagono regolare, perchè tale solido è basato sul pentagono, e quindi sulla sezione aurea, detta anche "divina proporzione"!
	Ecco un bellissimo icosaedro stellato, solido ricavato dall'icosaedro regolare. Si tratta di un solido platonico con 20 facce, 30 spigoli e 12 vertici; le facce sono triangoli equilateri. Per saperne di più sull'argomento di questi poliedri, vi consiglio vivamente di leggere questo articolo a firma dell'amico Livio Zefiro.
	Ed ecco come l'amica Gloria Nobili ha realizzato con il cartoncino un poliedro molti particolare: il cubottaedro stellato! Il cubottaedro semplice è uno dei tredici poliedri archimedei conosciuti, e lo si vede in alto a detra, colorato in giallo e rosso, nella figura soprastante. Per ottenere il corrispondente poliedro stellato, ad ogni faccia si aggiungono delle piramidi fatte di triangoli equilateri. L'effetto tridimensionale è sicuramente spettacolare!
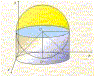
	Dicesi scodella di Galileo il solido delimitato da una semisfera e dal cilindro ad essa circoscritto che ha come base il suo cerchio massimo e come altezza il suo raggio. Mediante il principio di Cavalieri si dimostra che essa è equivalente al cono che ha la stessa base e la stessa altezza del cilindro considerato, e questo risultato è utilizzato per determinare il volume della sfera.
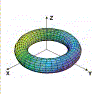
	Questo è un toro, superficie ottenuta facendo ruotare una circonferenza attorno ad una retta ad essa complanare e che non la attraversa. Il toro è stato reso famoso dall'ingegneria moderna, perchè un reattore nucleare a fusione dovrebbe avere proprio una geometria toroidale (è con una tesi su questo argomento che si è laureato l'autore di questo sito).
	Ecco una superficie famosissima: è l'ellissoide, superficie chiusa del secondo ordine le cui sezioni sono delle ellissi. La sua equazione cartesiana è x²/a² + y²/b² + z²/c² = 1, dove a, b e c sono i tre semiassi. Se a = b = c l'ellissoide diventa una superficie sferica. È una quadrica come tutte le superfici espresse da equazioni di secondo grado.
	La superficie sferica è una figura geometrica di equazione x² + y² + z² = r² (r è il suo raggio), definibile come il luogo dei punti equidistanti da un punto fisso detto centro. La sfera è il luogo dei punti interni ad una superficie sferica. Come si vede dalla foto accanto, una figura così regolare e perfetta ha ispirato da sempre la storia dell'arte: è il caso di questa moderna fontana in cui l'acqua fuoriesce dalla base di una sfera rotante!
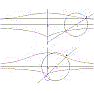
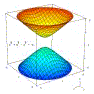
	Questa superficie è nota come iperboloide a due falde ed ha equazione cartesiana x²/a² + y²/b² – z²/c² = – 1. Insieme all'ellissoide, alla sfera e al paraboloide forma la famiglia delle quadriche, superfici la cui equazione cartesiana obbedisce ad un'equazione di secondo grado in x, y e z.
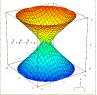
	Questa superficie è nota come iperboloide ad una falda ed ha equazione cartesiana x²/a² + y²/b² – z²/c² = 1. A differenza della precedente è una quadrica rigata, cioè in essa giace una famiglia di rette.
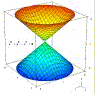
	Questa superficie è invece un iperboloide degenere di equazione cartesiana x²/a² + y²/b² – z²/c² = 0. Come si vede, essa degenera in una comune superficie conica.
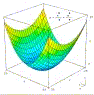
	Questa superficie è nota come paraboloide ellittico ed ha equazione cartesiana z = x²/a² + y²/b². Esso fa parte della famiglia delle quadriche, ma non è una quadrica rigata.
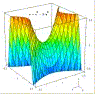
	Questa superficie è nota come paraboloide iperbolico ed ha equazione cartesiana z = x²/a² – y²/b². A differenza del precedente esso è una quadrica rigata; viene chiamata anche "superficie a sella". E con questo chiudiamo la galleria delle superfici disegnate con Derive 5.
	Impossibile non fare un cenno all'elica cilindrica, che è alla base del funzionamento delle comuni viti, visibili in questa fotografia. L'elica cilindrica è una linea in tre dimensioni che può essere avvolta con un angolo costante sulla superficie di un cilindro. Non solo la filettatura di una vite, ma anche una molla, una pompa elicoidale, una scala a chiocciola e la struttura del DNA sono basate su di essa, e così la magnifica decorazione della colonna Traiana a Roma!
	Apriamo ora un nuovo capitolo, nel quale ci occuperemo, in termini molto semplici, del cosiddetto calcolo delle variazioni. Si tratta di una complessa branca della matematica che studia la situazione in cui una determinata grandezza risulta minima sotto certe condizioni: per esempio, il minimo percorso necessario per toccare un certo numero di città decise in anticipo. Per descrivere questo argomento mi servirò di alcune fotografie da me scattate durante una lezione pratica con il consenso della collega Claudia Bina, che ringrazio sentitamente. Ma perchè "bubbles"? Cosa c'entrano le bolle di sapone, che in questa fotografia si vedono realizzate con opportune intelaiature metalliche di forme svariate?
	C'entrano eccome perchè, nel suo libro "Statique expérimentale et théorique des liquides sounzis aux seuls fòrces moléculaires" (1873), il matematico francese Antoine-Ferdinand Plateau (1801-1883) dimostrò che le lamine di acqua saponata si dispongono sempre lungo superfici di area minima, dette appunto superfici minime. Lo dimostra questo telaio formato da due asticelle colorate e da due cordicelle: una volta che in esso si forma una lamina di acqua saponata, le cordicelle si curvano in modo che la superficie della lamina sia la minima possibile, fissata la lunghezza delle corde (questo viene anche chiamato problema di Plateau). Spettacoloso, vero?
	Si può ripetere l'esperimento precedente in tre dimensioni anziché in due? Certamente. Immergiamo in acqua saponata una struttura di filo di ferro formata da due cerchi paralleli abbastanza vicini. La superficie che si ottiene generalizza il problema dimensionale precedente, e prende il nome di catenoide!
	La foto a fianco è stata ottenuta immergendo in acqua saponata due fogli di plexiglas separati da tre viti, e ci aiuta a risolvere genialmente l'annoso problema di Steiner: congiungere tre città con un sistema di strade di minima lunghezza totale. Come si vede, le lamine saponate danno vita esattamente a superfici minime, le quali incredibilmente formano angoli di 120°: un angolo da tenere a mente, perchè ricorre innumerevoli volte in natura!
	Lo stesso risultato si ottiene ponendo una accanto all'altra tre bolle sferiche di uguali dimensioni: anch'esse formano, inevitabilmente, il magico angolo di 120°! Lo si vede molto bene in questa fotografia, in cui il contrasto è stato esaltato artificialmente per esaltare la curvatura delle bolle e l'angolo che esse formano. E non è finita qui...
	...Se infatti immergiamo nell'acqua saponata un telaio di forma cubica, si ottiene una struttura estremamente spettacolare, formata da 4 triangoli, 8 trapezi ed un quadrato centrale (praticamente al centro si disegna un cubetto più piccolo). Le varie superfici si incontrano tra loro... indovinate un po'... formando proprio angoli di 120°!
	Voi direte: che ci fa mai un alveare in questo Armadio Virtuale, essendocene già un esemplare in quello di Zoologia? Perchè voglio far notare che anche queste cellette di cera sono costruite, incredibilmente, a forma di esagoni regolari, in modo che le pareti formino fra di loro angoli di 120°!! Non si sa come le api conoscano il calcolo delle variazioni ma, operando in questo modo, esse ottengono un massimo di capienza con un minimo dispendio di cera!!
	E non è il solo caso in cui la natura sembra conoscere la matematica meglio dei matematici umani. Si considerino queste cellule di cipolla osservate a forte ingrandimento: anch'esse appaiono né più, né meno, che come un pavimento di piastrelle poligonali in cui predominano gli angoli vicini a 120°. In tal modo il volume delle cellule diventa il massimo con il minimo contorno, e quindi esponendo la minima superficie al pericoloso mondo esterno. Davvero in fotografie come questa è difficile non riconoscere una di quelle che Hegel definiva "le astuzie della ragione" e che, per i credenti, rappresentano la firma del Creatore!
	L'architetto tedesco Otto Frei (1925-vivente) usò le pellicole di acqua saponata per disegnare strutture architettoniche, convinto com'era (ed ormai lo siamo anche noi!) che la natura tende spontaneamente a dar vita a forme ottimali. Egli conficcò degli aghi in una superficie, tese tra di essi fili sottilissimi, immerse il tutto in acqua saponata ed ottenne una lamina che aveva la forma di una tenda. Frei sfruttò questa, che chiamò una tensostruttura, per costruire l'Olympiastadion di Monaco di Baviera per le Olimpiadi del 1972. In figura se ne vedono alcuni modellini realizzati dagli studenti della V I a.s. 2006/2007.
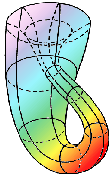
	Ancora alcune curiosità prima di chiudere. Questa foto digitale ritoccata raffigura un anello di Moëbius costruito dal sottoscritto. Si tratta di un anello ottenuto prendendo una striscia di carta, facendo ruotare di 180° uno dei suoi estremi ed incollandolo sull'altro estremo. Si tratta di una superficie con una sola faccia, priva cioè di superficie interna e di superficie esterna, ideata da August Ferdinand Moëbius (1790-1868), uno dei fondatori della topologia.
	Felix Klein (1849-1925) fu l'ideatore del cosiddetto « programma di Erlangen » (1872) a proposito della ricerca dei gruppi di trasformazioni geometriche e dei loro invarianti. Ma i suoi contributi alla geometria furono anche altri: sua, ad esempio, è l'idea della bottiglia di Klein qui raffigurata. Si tratta, sorprendentemente, di una figura solida con una sola faccia, e quindi priva di esterno e di interno: un vermiciattolo che strisciasse sulla sua superficie potrebbe tranquillamente passare dall'interno all'esterno senza attraversare nessuno spigolo. Si tratta quindi di una generalizzazione dell'anello di Moëbius sopra presentato!
	Ed ecco un meraviglioso esemplare di bottiglia di Klein realizzata in pratica in cristallo, ed acquistata negli Stati Uniti d'America. Versando liquido nell'imboccatura, esso percorre tutto il volume della bottiglia, che dimostra di non avere né un "dentro" né un "fuori". Si noti che la bottiglia è difficilissima da pulire al suo interno. Per questo non bisogna mai versarvi acqua, che lasci aloni, bensì alcool puro, che evapora senza lasciare alcuna traccia!
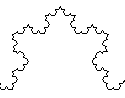
	Quella qui illustrata è una curva di Koch, dal nome del matematico svedese Helge von Koch (1870-1924) che la ideò. La si può costruire così: preso un segmento, lo si divide in tre parti uguali, su quello centrale si costruisce un triangolo equilatero e se ne prendono solo i due lati non allineati al segmento. Poi la stessa operazione viene ripetuta con ciascuno dei quattro segmenti così ottenuti, ottenendo una poligonale di 16 lati; il procedimento viene iterato per ciascuno dei suoi sedici lati, e così via all'infinito. La curva così ottenuta ha la particolarità di essere continua ma non derivabile in ogni suo punto.
	La caratteristica principale della curva di Koch sta nel fatto che ogni singola parte, per quanto piccola, riproduce il tutto. Questo principio è alla base di quelli che sono oggi comunemente conosciuti con il nome di frattali. Incredibilmente, anche questi rami di conifera hanno una struttura frattalica: come si può osservare aguzzando la vista, ogni singola ramificazione riproduce, in piccolo, la struttura dell'intero ramo! La struttura del mondo che ci circonda è dunque frattalica.
	Potrà sembrarvi incredibile, ma persino un broccolo romanesco (Brassica oleracea) rappresenta un bell'esempio di frattale autosomigliante, come dimostra questo confronto tra un "vero" broccolo da me stesso comprato al supermercato, e un frattale generato dal Pc che somiglia in tutto e per tutto al primo! Eugenio Azpeitia e colleghi dell’Università di Lione hanno chiarito nel 2021 alcuni dei meccanismi genetici che guidano lo sviluppo di queste strutture. L’infiorescenza del broccolo romanesco assume quel tipico aspetto perché i boccioli dei fiori non maturano mai fino a raggiungere lo stadio floreale, ma generano sempre nuove infiorescenze della stessa struttura di quella su cui si formano, e ciò dà vita all'autosomiglianza tipica dei frattali!
	Anche i disegni sulle ali di questa farfalla, come si vede, rappresentano un frattale con la proprietà dell'autosomiglianza: ogni parte più piccola riproduce il disegno dell'intera ala. Si noti che questo frattale imita a perfezione quello disegnato dalle rugosità del tronco di una pianta d'alto fusto: è la somiglianza tra questi due frattali su esseri viventi incredibilmente diversi tra loro, a rendere possibile il fenomeno del mimetismo (vedi l'Armadio Virtuale di Zoologia)
	Anche questa foto composita, che mostra delle spirali di fumo, può sembrare fuori posto in questo Armadio Virtuale; ed invece, essa illustra ottimamente la cosiddetta Matematica del Caos. Esiste un'equazione deterministica che descrive queste spirali di fumo, in grado cioè di prevederne l'andamento a partire da prefissate condizioni iniziali? No, a partire da identiche condizioni esse possono dare vita a volute molto diverse: questo perchè le equazioni che le descrivono sono non lineari, e quindi imprevedibili. Questo fatto viene sintetizzato nell'effetto farfalla: una farfalla sbatte le ali a Milano, e questa minima perturbazione è sufficiente per cambiare il tempo a Rio de Janeiro!
	Questa curiosissima immagine illustra il principio olografico. Secondo tale principio, non ancora dimostrato, esiste un tetto massimo di contenuto informazionale di ogni regione adiacente ad una certa superficie. Per questo l'informazione contenuta in una scatola non dipende dal suo volume, ma dalla superficie delle pareti. Il principio fu postulato dal fisico Gerard't Hooft nel 1993, ed il suo nome deriva dall'analogia con l'ologramma, in cui un'immagine tridimensionale viene ottenuta proiettando delle immagini da uno schermo tridimensionale. Ah, quasi dimenticavo: quest'immagine è costruita a partire dalla fotografia di una teiera. Mi sembrava giusto chiudere con questa ardita speculazione il nostro grande Museo Virtuale.

Torna alla galleria immagini del mio sito