![]()
|
"Era come un liquor suttile e molle, L.Ariosto, "Orlando Furioso", XXXIV 83 |
.
3.1 Le leggi dei gas ideali
In quel che segue appunteremo la nostra attenzione unicamente sui gas. Questi, a differenza dei solidi e dei liquidi, risultano facilmente comprimibile, sicché è facile misurarne la dipendenza tra volume e pressione. Questo spiega il perchè, già nel XVII secolo, furono stabilite quelle che sono note come leggi dei gas. Vediamole una per una.
A) LEGGE DI BOYLE. A temperatura costante, cioè lungo una trasformazione isoterma, pressione e volume risultano inversamente proporzionali.
In altre parole, PV = cost.
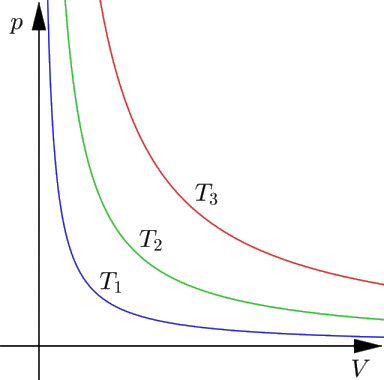
Se dunque rappresento nel piano PV le isoterme, cioè le trasformazioni a temperatura costante, per un sistema gassoso ho dei rami di iperbole equilatera, come in figura. Al crescere della temperatura (T3 > T2 > T1), si osserva che K cresce e l'iperbole si alza. Se V tende all'infinito, P tende a zero: il gas si dice allora estremamente rarefatto.
B) LEGGE DI CHARLES. A pressione costante, cioè lungo una trasformazione isobara, l'aumento di volume è proporzionale all'aumento di temperatura.
In altre parole, ΔV = α ΔT. Se V0 è il volume quando T = T0 (la temperatura di riferimento), la precedente diventa:
V – V0 = α ( T – T0 )
cioè:
V = V0 + α ( T – T0 )
La relazione tra T e V è dunque di tipo rettilineo. Se T0 = 0°C, come si fa di solito, allora V0 è il volume del gas a 0°C, e la precedente si può scrivere:
![]()
Sperimentalmente si verifica una cosa inaspettata: α/V0 ha lo stesso valore per tutti i gas, e vale 1/273,15 °C–1. La precedente allora diventa:
Tale legge prende il nome dal fisico francese Jacques Alexandre César Charles (1746-1823).

C) LEGGE DI GAY-LUSSAC. A volume costante, cioè lungo una trasformazione isocora, l'aumento di pressione è proporzionale all'aumento di temperatura.
In altre parole, ΔP = α ΔT. Ragionando analogamente al caso precedente si arriva a scrivere la relazione:
![]()
Amche in questo caso la costante α è pari a P0/273,15. Si perviene perciò alla formula:
Tale legge prende il nome dal fisico francese Joseph Louis Gay-Lussac (1778-1850).

Le ultime due leggi ci dicono che, al variare della temperatura, pressione e volume si comportano allo stesso modo! In realtà le tre leggi dei gas valgono solo per una particolare categoria di gas: i gas ideali.
Si dice gas perfetto o gas ideale un gas che soddisfa le due seguenti condizioni:
a) le molecole che lo compongono sono puntiformi, cioè il loro volume proprio è nullo;
b) le molecole non interagiscono tra di loro né con interazioni di natura chimica, né elettromagnetica, né gravitazionale, né nucleare. Esse interagiscono solo attraverso urti elastici.
Nessun gas del nostro universo si può considerare perfetto; tuttavia, un gas reale può comportarsi in maniera molto vicina s un gas ideale se a sua volta soddisfa due condizioni:
I) è estremamente rarefatto. Infatti in tal caso la pressione è bassissima e il volume molto grande. Le distanze intermolecolari allora sono molto grandi rispetto alle dimensioni delle particelle, cosicché ognuna di esse vede le altre come dei corpi puntiformi, e soddisfa alla condizione a).
II) è molto lontano dalla temperatura di liquefazione (vedi paragrafo 2.1). Questo vuol dire che la temperatura del gas è molto alta; ma allora la velocità delle molecole è molto alta, e quando esse si urtano, non fanno in tempo ad interagire in alcun modo; l'urto è totalmente elastico, giacché l'energia si conserva, e anche la condizione b) è soddisfa.
In pratica, l'aria della stanza in cui ora vi trovate si comporta abbastanza bene come un gas perfetto ,perché è rarefatta (tra voi e lo schermo del computer non vedete alcuna nebbia) e molto lontana dalla temperatura di liquefazione, che a 1 atmosfera è pari a – 194,4ºC, visto che nella stanza in cui mi trovo ora il termometro digitale segna + 20,3°C: oltre duecento gradi al di sopra di quella a cui l'aria condensa! E così, compiendo esperimenti con l'aria a temperatura ambiente, le leggi dei gas sopra scritte risultano verificate in modo più che soddisfacente.
.
3.2 Lo zero assoluto
Proviamo ora ad estrapolare il diagramma disegnato per illustrare la Legge di Charles, cioè a prolungarlo a temperature più basse di 0°C. Come si vede, ipotizzando che la suddetta legge continui a valere, si arriva ad una temperatura cui corrisponde un volume nullo!

Infatti, se nella (3.1) poniamo V = 0, si ha 1 + 1/273,15 = 0, da cui T = – 273,15°C. È come se a questa temperatura il gas "cessasse di esistere"!
La possibilità che il volume diventi nullo è legato alle approssimazioni del gas perfetto elencate sopra. Infatti, se le molecole sono davvero puntiformi, ognuna di esse ha volume nullo, e quando si avvicinano l'una all'altra il condensato ha anch'esso volume nullo. Il numero di Avogadro è veramente enorme, se confrontato agli ordini di grandezza della nostra vita quotidiana, ma anch'esso, se è moltiplicato per zero, restituisce sempre un valore nullo.
In realtà, questa estrapolazione è poco realistica, perchè (come si è detto) il gas perfetto è incondensabile, mentre i gas reali a un certo punto liquefano; e infatti le tre leggi dei gas perfetti valgono solo lontano dal punto di liquefazione. L'estrapolazione sopra fatta non rispecchia dunque il vero comportamento dei gas reali. È però vero che non è possibile scendere sotto la temperatura di – 273,15°C. Tale temperatura si chiama zero assoluto, e rappresenta un'effettiva situazione fisica di grande importanza concettuale.
Ciò significa che, mentre non c'è una temperatura maggiore di tutte, ce n'è invece una più bassa in assoluto, da cui il nome. Interessante è notare che in una puntata della seconda stagione del noto telefilm di fantascienza "Star Trek - The Next Generation", e in particolare in quella intitolata "Hotel Royale" (il titolo originale è "The Royale"), l'Ufficiale Scientifico Geordi la Forge afferma che la superficie del pianeta Theta VIII attorno a cui l'Enterprise-D sta orbitando ha una temperatura di meno 291 gradi Celsius, cioè ben 18 gradi Celsius sotto lo zero assoluto! (vedi questo sito) Purtroppo per La Forge, ciò che è assoluto oggi lo sarà anche nel XXIV secolo; dunque questa informazione lascia credere che ci fosse un guasto nei sistemi di rilevazione dati dell'Enterprise-D (o più probabilmente una vistosa lacuna nella preparazione in Fisica degli sceneggiatori di quel telefilm!)
Per questo a William Thomson, Primo Barone di Kelvin (1824-1907), venne l'idea di adottare una nuova scala termometrica, che abbia lo zero proprio nello zero assoluto. In tal modo si eviterebbe l'incomodo di usare temperature negative. Questa scala prende il nome di Scala Assoluta o Scala Kelvin, e le temperature da essa misurate prendono il nome di temperature assolute. Tale scala è l'unica effettivamente utilizzata in Termodinamica. L'unità di misura viene chiamata Kelvin (fino al 1961 "grado Kelvin", oggi questo termine non è più utilizzato). Il suo simbolo è K, ed è identico al grado Celsius. In altre parole, le differenze di temperatura sono identiche nelle due scale. Quale la relazione tra la temperatura assoluta e quella Kelvin?
T [K] = 273,15 + t [°C]
Nel 1954, al fine di usare un'unità di misura standard della temperatura, venne introdotta una nuova definizione di Kelvin: esso è pari a 1/273,16 della temperatura assoluta del punto triplo dell'acqua (0,02°C).
A dir la verità, esiste un'altra importante scala termometrica, e vale la pena di accennare ad essa. Siccome il Kelvin è equivalente al grado Celsius, mentre nei paesi anglosassoni è molto più in uso il grado Fahrenheit (vedi § 1.4), era logico che qualcuno provasse a mischiare le carte. Venne così introdotta la Scala Rankine, dal nome dell'ingegnere scozzese William John Macquorn Rankine (1820-1872): il grado Rankine (°R) è identico al grado Fahrenheit, ma lo zero della scala è posto nello zero assoluto, esattamente come nella scala Kelvin. Siccome lo zero assoluto equivale a − 459,67 °F, per passare dalla scala Fahrenheit a quella Rankine basterà sommare 459,67 a tutte le temperature. Per passare dalla scala Celsius a quella Rankine occorre invece usare questa formula:
![]()
Mentre per passare da Rankine a Celsius c'è la formula inversa:
![]()
Ad esempio, 100°C equivalgono a 671,67°F.
Torniamo ora ai Kelvin. Usando la scala assoluta, la Legge di Charles (3.1) assume la forma:
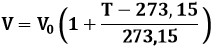
cioè:
![]()
Dunque esiste un'effettiva proporzionalità diretta tra volume e temperatura assoluta, proporzionalità che non esisteva per le temperature Celsius. Stessa cosa accade tra pressioni e temperature assolute:
![]()
dove P0 e V0 sono i valori di pressione e volume del gas a 0°C = 273,15 K. Ecco perchè il Kelvin è una delle unità fondamentali del Sistema Internazionale di misura, insieme al metro, al chilogrammo, al secondo e all'Ampére.
William Thomson, Primo Barone di Kelvin
3.3 L'equazione di stato dei gas ideali
Sulla scorta di quanto detto finora, possiamo ricavare un'equazione che lega tra loro le variabili caratteristiche di due stati differenti dello stesso gas ideale. Consideriamo questi due stati A e B, caratterizzate dai parametri A ( PA , VA , TA) e B ( PB , VB , TB ). Supponiamo che TA < TB, come in figura:
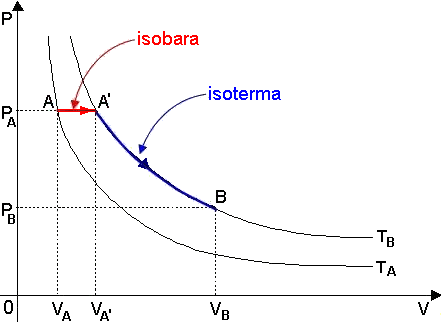
Si può andare dall'uno all'altro in questo modo: prima mi sposto da A ad A', con la stessa pressione di A e la stessa temperatura di B, lungo una trasformazione isobara (in rosso), e poi mi sosto da A' a B lungo un'isoterma (in blu), perchè hanno la stessa temperatura. Per la legge di Charles lungo AA', si ha che:
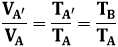
Da cui:
![]()
Ora applico la legge di Boyle lungo A'B, ed ho:
![]()
Sostituendovi la precedente, diventa:
![]()
che si può riscrivere:
![]()
Se ne deduce un fatto molto importante: per un gas ideale, il prodotto tra pressione, volume e reciproco della temperatura è costante!
![]()
Non è difficile rendersi conto che il volume di un gas è proporzionale al numero n di moli che esso contiene, per cui la costante di proporzionalità dovrà contenere tale numero. Detta R la costante di proporzionalità, avremo:
![]()
che di solito si scrive così:
Questa si chiama equazione di stato dei gas perfetti, perchè lega tra di loro le variabili di uno stato termodinamico. La costante R viene chiamata costante dei gas perfetti, e si può dimostrare che si tratta di una costante universale. Quanto vale? Noi sappiamo che una mole di gas perfetto, alla temperatura di 0°C = 273,15 K e alla pressione di 1 atm, occupa un volume (detto volume molare) di 22, 414 litri. Allora:
![]()
Se misuro la pressione in atmosfere e il volume in litri ("unità tecniche"), il lavoro si misurerà con un'unità chiamata litriatmosfere, e dunque R sarà misurata in l atm / K mol. Se vogliamo passare in unità del Sistema Internazionale, siccome il lavoro sarà misurato in Joule, avremo:
![]()
E operando in calorie:
R = 8,314 / 4,186 = 1,98 Kcal / mol K
A partire dalla (3.3) possiamo affermare quanto segue:
se T è costante, P V = cost., e così ritroviamo la Legge di Boyle.
se P è costante, si ritrova V/T = cost., cioè la Legge di Charles.
se V è costante, si ritrova P/T = cost., cioè la Legge di Gay-Lussac.
La (3.3) però è più generale, perchè vale per tutti gli stati termodinamici. Occorre sottolineare tuttavia che non è di validità assoluta, ma ha senso solo per i gas perfetti; per i gas reali, P V non è più esattamente pari ad n R T. Il rapporto:
![]()
si chiama allora fattore di comprimibilità. Se il gas è ideale, per una mole di gas esso vale esattamente uno. Per cinque diversi gas ideali, il suo comportamento al variare della pressione è illustrato da questo grafico:
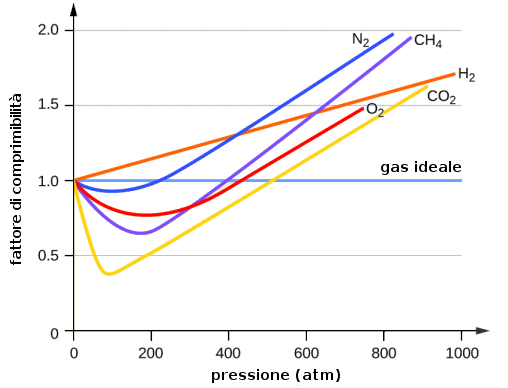
Come si vede, a bassa pressione tutte e cinque le curve tendono al valore uno, perchè tutti i gas rarefatti, a bassissima pressione, tendono a comportarsi come gas ideali, per i quali vale la (3.3).
Se invece del numero di moli si conosce la massa m del nostro gas, basta tenere presente che:
m = M n
dove M è la massa molare del gas. Allora la (3.3) diventa:
![]()
Ricordiamo che la massa molare è la massa di una mole di gas, pari in grammi al suo peso molecolare. Se invece N è il numero di molecole e NAV è il numero di Avogadro, avremo:
![]()
Esempio 3.1: Un cilindro munito di stantuffo contiene 8 g di ossigeno (O2) alla pressione di 1 atmosfera e alla temperatura di 27°C. Quale volume occupa il gas?
Anzitutto, una mole di ossigeno ha un massa di 32 g, per cui:
n = 8 g / 32 g mol–1 = 0,25 mol
Inoltre T = 27 + 273,15 = 300, 15 K. Ne consegue:
![]()
Esempio 3.2: In un tubo a raggi X è presente una pressione residua di 7,6 x 10–6 torr. Sapendo che ha un volume di 600 cm3 e si trova a 26°C, quante molecole d'aria contiene?
Tanto per cominciare:
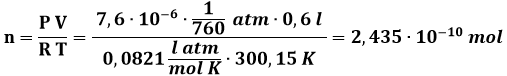
Purtroppo l'aria è un miscuglio di gas, e precisamente è composta dal 79 % di azoto e dal 21 % di ossigeno (trascuriamo piccole percentuali di altri gas). Qual è dunque la sua massa molare? Usiamo una media pesata:
Maria = 0,79 x Mazoto + 0,21 x Moss. = 0,79 x 28 + 0,21 x 32 = 28,9 g mol–1
La massa dell'aria è dunque:
maria = n x Maria = 7,036 x 10–9 g
E quanto al numero di molecole:
N = n x NAV = 1,47 x 1014 molecole
.
3.4 Isoterme dei gas reali
Vediamo ora il comportamento di quelli che si chiamano i gas reali. Anzitutto queste, a differenza dei gas ideali, cambiano di stato, cioè possono liquefare. Un gas può venire liquefatto in due modi:
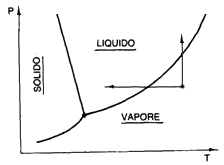 i)
abbassandone la temperatura a pressione costante
(così condensa il vapore acqueo sul cruscotto dell'auto);
i)
abbassandone la temperatura a pressione costante
(così condensa il vapore acqueo sul cruscotto dell'auto);
ii) oppure comprimendolo a temperatura costante (così si realizzano le bombole di gas da cucina e gli spray).
I due procedimenti sono illustrati qui a fianco dalle due frecce nel diagramma. Fin dal 1860 il chimico nordirlandese Thomas Andrews (1813-1885) mise in evidenza il fatto che, qualunque sia la pressione agente, è impossibile liquefare un gas se esso si trova al di sopra di una certa temperatura, detta temperatura critica. Questo è il discrimine tra vapore e gas; vale infatti la:
Def. 3.1: Dicesi gas un aeriforme che non può venire liquefatto per sola compressione.
Consideriamo dunque una mole di gas reale. A basse temperature esso si presenta liquido, e le isoterme del liquido nel piano P,V sono praticamente verticali, poiché esso è quasi incomprimibile. Ad un certo punto però, diminuendo la pressione, il liquido comincia a bollire, ed allora per un certo tempo si ha la coesistenza di due fasi. Poiché ciò avviene a pressione costante, la linea che ne risulta è quasi orizzontale. Alla fine, quando tutto il liquido è diventato vapore, al diminuire di P il gas si approssima alle condizioni di gas perfetto, e e dunque l'isoterma viene ad avvicinarsi ad un ramo di iperbole equilatera.
Questa avviene a temperatura T fissata. E se alzo la temperatura del mio fluido? Mi accorgo che il tratto orizzontale comincia più avanti di quanto era successo prima e termina più indietro, cioè è più corto. Naturalmente questa seconda isoterma si trova a pressione più alta di quella precedente, perchè la tensione di vapore aumenta con la temperatura. Per temperature via via crescenti, come si vede qui sotto, il tratto orizzontale si accorcia via via, fino a che non... si annulla. In questo caso, la condensazione avviene istantaneamente. Questo punto viene detto punto critico, e la sua temperatura, che per l'acqua vale 373°C e per la CO2 vale 21°C, è appunto la temperatura critica. Infatti, a temperature superiori a questa, l'aeriforme non raggiunge più lo stato liquido, qualunque sia la temperatura a cui esso si trova. Per questo, al di sopra dell'isoterma critica, si ha lo stato gassoso propriamente detto. Se congiungo i punti iniziali e finali dei plateau di cambiamento di fase, ottengo una curva detta campana di Andrews. Nel caso dell'anidride carbonica (CO2), il diagramma assume questo aspetto:
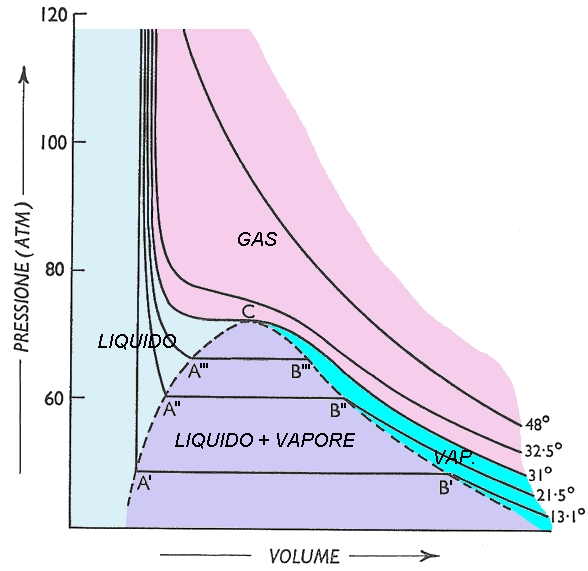
La campana di Andrews è detta curva di saturazione. Infatti, i punti A', A'', A'''... sono i punti in cui il liquido è saturo, cioè l'ebollizione sta cominciando, anche se la miscela è ancora formata dal 100 % di liquido. Invece i punti B', B'', B'''... sono quelli in cui il vapore è saturo, cioè il liquido ha ormai finito di evaporare, si ha il 100 % di vapore ma la temperatura non ha ancora cominciato a salire oltre a quella di ebollizione. I punti dei segmenti A'B', A''B'', A'''B'''... sono invece stati in cui liquido e vapore convivono. In che percentuale?
Def. 3.2: Dicesi titolo di vapore x la percentuale sul totale del vapore nella miscela liquido + vapore. In altre parole:
![]()
Per il liquido saturo è x = 0; per il vapore saturo è x = 1. Le curve con x = costante si dicono curve isotitolo.
Invece, i punti compresi tra l'isoterma critica e la curva isotitolo con x = 0 rappresentano stati in fase liquida, mentre quelli tra l'isoterma critica e la curva isotitolo ad x = 1 rappresentano stati in fase vapore. La campana di Andrews racchiude invece stati bifase. Per questo ho diviso il diagramma PV soprastante in aree di colore diverso dipendenti dalla loro fase. Sopra l'isoterma critica ho ovviamente stati in fase gassosa; in esso le isoterme hanno una certa deviazione dall'iperbole equilatera, ma ci si avvicinano sempre più quando la temperatura cresce, in accordo con quanto detto sopra. Da tutto questo si deduce che:
a) i gas reali si comportano con ottima approssimazione come gas ideali, per temperature inferiori a quella critica, solo nella regione di vapore sovrassaturo;
b) sopra l'isoterma critica la mia sostanza fluida si comporta sempre come un gas, poiché l'energia perduta dalle molecole è così grande che, qualunque sia la pressione agente, esse si comportano sempre come se fossero del tutto indipendenti;
c) sotto l'isoterma critica, quando l'energia cinetica diminuisce a sufficienza, prevale l'energia potenziale di interazione tra le molecole, che danno il via al processo di condensazione.
Johannes Diderik van der Waals
.
3.5 L'equazione di van der Waals
Siccome, come si vede, i gas reali si discostano parecchio dal comportamento previsto per i gas ideali, era logico che qualcuno provasse a determinare un'equazione valida anche per essi. In particolare questo fu l'intento del fisico olandese Johannes Diderik van der Waals (1837-1923), che in un articolo del 1873 ("Over de Continuïteit van den Gas - en Vloeistoftoestand", "Sulla continuità dello stato liquido e gassoso") propose di modificare l'equazione (3.3) tenendo conto che:
1) nei gas reali il volume materialmente occupato dalle molecole non è affatto trascurabile rispetto al volume del recipiente. A tale volume proprio delle molecole si dà il nome di covolume.
2) nei gas reali tra le particelle esistono forze di interazione non trascurabili.
L'equazione scritta da van der Waals è la seguente:
Per la formulazione di questa legge, van der Waals fu insignito del Premio Nobel per la fisica nel 1910. I valori di a e di b vengono ricavati sperimentalmente; a si misura in atm l2 / mol2 e b in l / mol. Infatti n b deve avere le dimensioni di un volume, rappresentando il suddetto covolume (b rappresenta perciò il covolume molare), e a n2 / V2 quelle di una pressione. Ecco i valori di a e di b per alcuni gas:
|
Gas |
a |
b |
|
He |
0,034 |
0,024 |
|
H2 |
0,25 |
0,027 |
|
O2 |
1,39 |
0,032 |
|
CO2 |
3,60 |
0,043 |
|
HCl |
3,70 |
0,041 |
|
H2S |
4,40 |
0,043 |
|
H2O |
5,46 |
0,030 |
|
Cl2 |
5,50 |
0,049 |
Per una sola mole di gas, la (3.4) diventa:
![]()
sviluppando i calcoli, otteniamo:
![]()
Quindi, rispetto all'equazione dei gas ideali P V = n R T, van der Waals ha aggiunto tre termini correttivi, uno positivo e due negativi. L'entità di tale correzione diminuisce al diminuire della pressione ed all'aumentare del volume, mentre ad alte pressioni si accentua, come è naturale che sia. Se rappresentiamo la (3.4) per T costante, dopo aver risolto rispetto a P, si ricava una curva come quella qui sotto.
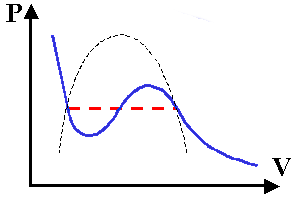
Al posto del plateau essa ha due gobbe, per cui anche questa equazione non rappresenta una descrizione corretta del comportamento dei gas reali. Ce ne renderemo conto con un esempio.
Esempio 3.3: Sia data una mole di CO2 contenuta in un recipiente di 0,5 l a 50°C. Qual è la sua pressione?
Usando l'equazione di stato dei gas ideali, avrei:
![]()
Mediante l'equazione di van der Waals, invece, ottengo:
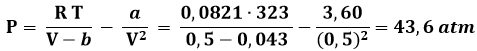
Sperimentalmente si ottiene un valore di 41,2 atm. Come si vede, il valore calcolato con l'ipotesi dei gas reali differisce da questo del 28,8 %, mentre quello calcolato con l'ipotesi di van der Waals differisce da esso solo del 5,8 %.
Si osservi che il covolume n b non è pari al volume geometrico totale delle molecole, come si potrebbe penare in un primo momento, ma è circa pari a quattro volte tale volume, a causa della forma reale (non cubica) delle molecole, che lascia spazi vuoti fra di esse, e delle forze repulsive che aumentano mano a mano che le loro atmosfere elettroniche si avvicinano; viene così impedito l'"impacchettamento" delle molecole stesse. Lo vedremo nel capitolo 9. L'equazione di van der Waals è un tipico esempio di legge semiempirica, perchè la struttura della formula può essere giustificata mediante considerazioni teoriche, ma i coefficienti a e b per ogni gas possono solo essere determinati sperimentalmente.
..
Naturalmente è d'obbligo chiedersi: una volta stabilite le leggi cui obbediscono i gas, che utilità posso trarne? Lo saprete passando con me al prossimo capitolo, nel quale introdurremo il concetto di Primo Principio della Termodinamica. Per tornare all'indice, invece, il link è questo.
![]()