![]()
|
"Gesù disse a Nicodemo: « In verità, in verità io ti dico, se uno non nasce dall'alto, non può vedere il regno di Dio. » Gli disse Nicodemo: «Come può nascere un uomo quando è vecchio? Può forse entrare una seconda volta nel grembo di sua madre e rinascere? »" Vangelo di San Giovanni 3, 3-4 |
.
5.1 Il concetto di irreversibilità
Si è già detti che il concetto fondamentale espresso dal Primo Principio della Termodinamica consiste nella conservazione dell'energia. L'energia può trasformarsi da una forma all'altra, ma no può né essere creata né distrutta; l'energia totale del sistema rimane costante. Tuttavia, questo principio non stabilisce alcun limite alla convertibilità dell'energia. In altre parole, tutte le energie di questo mondo risultano equivalenti ai fini delle possibili trasformazioni da una forma all'altra. In teoria, cioè, se io ho tot Joule di energia meccanica, essi possono essere integralmente trasformati integralmente trasformati in calore, e viceversa, tot Joule di energia termica possono venire trasformati in energia meccanica.
Eppure, l'esperienza comune ci dice che non è affatto così. Alcuni fenomeni di trasformazione dell'energia avvengono invariabilmente a senso unico. Per esempio, quando si arresta un'automobile agendo sul freno, questo si riscalda, e così i copertoni ed il fondo stradale; tuttavia, per quanto calore si possa cedere al freno, l'auto non si rimetterà mai in movimento, né sarà più possibile recuperare il calore gettato via durante la frenata per riavviare la macchina.
Analogamente, se si getta un grave da alta quota, oppure nell'oceano, l'energia gravitazionale si trasforma in energia termica, perchè il corpo ad un certo punto non accelera più, procede a velocità di regime, e l'energia di accelerazione si scarica nel mezzo, ma questo calore risulta praticamente inutilizzabile, essendo calore a bassa temperatura; né riscaldando la massa essa tornerà a salire verso l'alto. Se ne deduce che la natura fissa un verso privilegiato alle trasformazioni energetiche.
Si noti che, se stessimo osservando un filmato in cui sono ripresi dei fenomeni puramente meccanici, come urti elastici o moti su di una superficie priva di attrito, non potremmo in alcun modo sapere se l'operatore della cinepresa sta facendo girare la pellicola nel senso giusto o alla rovescia, poiché i fenomeni meccanici sono tutti perfettamente reversibili. Quando però spunta fuori il calore, le cose cambiano radicalmente. Infatti, se nel filmato vedessimo una pallina che, rotolando su una superficie scabra, improvvisamente accelera, dedurremo giustamente che il filmato è fatto girare nel verso contrario, perchè l'attrito può frenare i corpi, ma mai metterli in moto. Analogamente se vedessimo un bicchiere di acqua tiepida che improvvisamente si mette a bollire da sola ed in essa compare un cubetto di ghiaccio, concluderemmo la stessa cosa, che il film gira al contrario e che in realtà il cubetto di ghiaccio è immerso nell'acqua bollente, si scioglie del tutto e di conseguenza la temperatura dell'acqua si abbassa.
Ma non si tratta certo delle uniche trasformazioni unidirezionali. Si pensi a un fenomeno come quello dell'invecchiamento: se si fa la tara a film come "Il curioso caso di Benjamin Button", tratto da un racconto paradossale di Francis Scott Fitzgerald (1896-1940), nessuno può invecchiare al contrario: nessun fenomeno è più unidirezionale della nostra esistenza umana. E infatti, come si legge nella citazione posta al principio di questo capitolo, quando Gesù disse a Nicodemo che solo chi rinasce dall'alto può vedere il Regno di Dio (si riferiva al battesimo), il membro del Sinedrio gli domandò perplesso: "Come può nascere un uomo quando è vecchio? Può forse entrare una seconda volta nel grembo di sua madre e rinascere?" (Gv 3, 4) Nicodemo era un uomo di buon senso, ed evidentemente conosceva bene i Principi della Termodinamica!
E così, l'unidirezionalità è una costante della nostra vita quotidiana. Noi non vedremo mai i cocci di un vaso rotto sul pavimento che saltano di nuovo a ricostruire il vaso intero sulla mensola, né un fiore che ritorna bocciolo, né tantomeno abbiamo la possibilità di veder ricomporsi di fronte ai nostri occhi gli atomi che costituivano il corpo di Giulio Cesare nel 45 a.C., sovvertendo il tempo. Tutti questi fenomeni sono ammessi come possibili dal Primo Principio della Termodinamica, eppure semplicemente non avvengono. Lo stesso scorrere del tempo ha un verso preciso che non si può invertire, un verso detto freccia del tempo: non la si può invertire più di quanto non si possa far crescere una pianta al contrario fino a farla rientrare nel seme, o più di quanto si possa far risuscitare i morti. Per questo, i sogni di realizzare una macchina del tempo sul modello di quella immaginata da Herbert George Wells (1866-1946) nel suo omonimo romanzo e nel film da esso tratto nel 2002 (vedi locandina sottostante) sono destinati, per l'appunto, a rimanere sempre e solo sogni.

Siamo così venuti a confrontarci per la prima volta con quel fenomeno prepotente ed ineludibile che è l'irreversibilità. Osserviamo che questo fenomeno è tutt'altro che di secondaria importanza, e lo studio di esso non attiene certo solo alla filosofia o alla metafisica. Infatti, se fosse possibile convertire senza scrupoli di unidirezionalità il calore in lavoro e il lavoro in calore, in barba a quanto detto poco fa, potremmo realizzare quello che viene comunemente conosciuto con il nome di moto perpetuo di seconda specie. Del moto perpetuo di prima specie abbiamo già parlato nel § 4.4, e si è visto che esso intenderebbe creare lavoro dal nulla, il che è impossibile per via del Primo Principio della Termodinamica. Invece quello di seconda specie non viola alcun principio di conservazione, però non fa altro che prendere il lavoro convertito in calore attraverso gli attriti, riconvertirlo di nuovo in lavoro meccanico e riutilizzarlo per far girare la macchina. In tal modo, la macchina funzionerebbe all'infinito, senza alcuna perdita sotto forma di attrito! Una volta fornito l'impulso iniziale, otterremmo lavoro utile in modo continuo.
Qui sotto ad esempio vedete un progetto di veicolo capace di mantenersi in moto senza consumare energia, realizzato verso il 1900. Esso è basato su una ruota senza posizione di equilibrio collegata alle ruote motrici con una trasmissione meccanica;. Le ruote motrici sono inoltre tenute in movimento da un ventilatore che sfrutta il vento relativo provocato dal moto dei veicolo, e che dovrebbe compensare esattamente l'energia persa per attrito dalla ruota a sinistra, dalle ruote sull'asfalto e dal veicolo contro l'atmosfera:

Ora, se il moto perpetuo di prima specie è impedito dal Primo Principio della Termodinamica, esiste un Secondo Principio in grado di impedire anche quello di seconda specie. Tale principio può essere enunciato in modi vari e sofisticati, che si equivalgono però nella sostanza. In questo capitolo noi esporremo solo i due enunciati di Kelvin e di Clausius, anche se, storicamente, l'ordine in cui essi furono formulati è esattamente l'inverso. Le prime intuizioni riguardanti il concetto di irreversibilità sono da ascrivere a Nicolas Léonard Sadi Carnot (1796-1832), anche se ai suoi tempi non era ancora stato formulato neppure il Primo Principio con la dovuta chiarezza. La sua origine è da ricercarsi nel notevole impulso agli studi teorici di termodinamica, che era stato dato dal fiorire di innovazioni tecnologiche sul finire del XVIII e al principio del XIX secolo, cominciando ovviamente dalla macchina a vapore, realizzata nel 1765 per opera di James Watt dopo i tentativi falliti di Giovanni Battista della Porta (1606), Salomon de Caus (1615), Giovanni Branca (1622), Denis Papin (1679) e Thomas Newcomen (1705). Tale macchina a vapore ebbe il merito di trasformare, in modo continuo e razionale (e, ovviamente, geniale), il calore prodotto dalla combustione del carbon fossile in lavoro meccanico. Tutte le macchine termiche sviluppate in seguito, ed in particolare tutti i motivi alternativi a vapore che sfruttano il cosiddetto Ciclo Rankine (di esso parleremo nel capitolo 6), ricalcano lo schema della prima macchina a vapore, inventata per estrarre l'acqua dalle miniere di carbone del Galles e della Scozia, e che fa di Watt uno dei maggiori ingegneri di tutti i tempi.
.
5.2 L'enunciato di Kelvin
Def. 5.1: Si dice sorgente di calore o serbatoio di calore un sistema a capacità termica praticamente infinita. In altre parole, la sua temperatura a non varia apprezzabilmente né assorbendo una qualsivoglia quantità di calore, né cedendola.
Sono sorgenti di calore ad esempio il mare e l'atmosfera, a patto di ipotizzare un perfetto rimescolamento delle masse d'acqua e d'aria dovuto alle correnti, ai venti e ai fenomeni atmosferici. D'altro canto, sono sorgenti di calore anche la luce solare e una caldaia alimentata con continuità mediante carbone, petrolio, gas naturale o barre d'uranio.
Fissata questa definizione, potremo ora studiare il funzionamento delle suddette macchine alternative. In esse, la trasformazione di energia termica in energia meccanica viene effettuata adoperando un opportuno fluido che bolle, si espande e compie un lavoro verso l'esterno, a spese del calore sottratto alla sorgente. Evidentemente, per avere un processo continuativo, è necessario ricorrere a un dispositivo che possa ritornare periodicamente nelle posizioni di partenza; un dispositivo cioè che faccia uso di trasformazioni cicliche, poiché un sistema finito non può modificarsi all'infinito nello stesso senso (ad esempio un pistone non può veder muovere lo stantuffo all'infinito nella medesima direzione). È chiaro che quel fluido dovrà essere compresso, per esempio sottraendo il calore di compressione portandolo a contatto con una sorgente fredda. Questa seconda sorgente, a temperatura minore della prima, è chiamata refrigerante. In un dispositivo chiamato condensatore, esso sottrae calore al fluido, riportandolo nelle condizioni di partenza. Il processo ciclico dovrà perciò assorbire calore da una sorgente calda per cederlo ad una più fredda; per ogni ciclo la variazione di energia interna è nulla, poiché l'energia interna torna sempre alle condizioni di partenza; perciò, per il Primo Principio avremo:
ΔU = Σi Qi – W = 0
e cioè:
Σi Qi = W (5.1)
Lo schema di macchina ciclica che noi useremo è quello qui sotto: il sistema S, rappresentato dal fluido termodinamico, assorbe una certa quantità di calore Q1 da un serbatoio a temperatura T1, e cede per ogni ciclo una quantità di calore Q2 a una sorgente a temperatura T2 < T1.
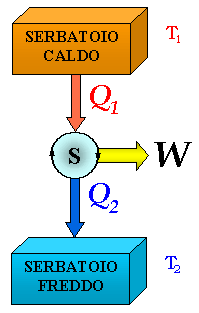
Il calore Q1 è positivo perchè entrante nel fluido del ciclo, quello Q2 è negativo perchè uscente, il lavoro W è positivo perchè compiuto dal sistema sull'ambiente. Per questo la (5.1) diventa:
Q1 – Q2 = W (5.2)
Questo prende il nome di Primo Principio della Termodinamica per Macchine Cicliche. In altre parole, non tutto il calore assorbito da una sorgente calda può essere convertito in lavoro meccanico, ma solo una parte, mentre la rimanenza viene scaricata ad una sorgente fredda, e quindi dissipata nell'ambiente.
Questo è il nocciolo del discorso. Nessuno è mai riuscito a produrre lavoro con continuità usando una sola sorgente di calore: una fredda a cui cedere parte del calore, fosse anche solo l'aria, ci deve pur essere. Se infatti si potesse fare, io potrei convertire interamente il calore in lavoro meccanico, anche quello perso per attrito, e quindi io potrei prendere un ruota, assorbire tutto il calore che essa dissipa per attrito lungo il perno e a contatto con l'aria, riconvertirlo in lavoro meccanico e cederlo alla ruota affinché continui a girare, praticamente per sempre. Insomma, avrei realizzato il famigerato moto perpetuo di seconda specie. Proprio per evitare questo, Lord Kelvin ha enunciato il:
SECONDO PRINCIPIO DELLA TERMODINAMICA, ENUNCIATO DI KELVIN: È tecnicamente e teoricamente impossibile realizzare una trasformazione termodinamica il cui unico risultato è quello di convertire interamente l'energia di una sola sorgente di calore in lavoro meccanico.
Bisogna sottolineare le parole "il cui unico risultato" ed "una sola sorgente". Infatti, si prenda in considerazione il seguente esempio. Sia un cilindro dotato di pistone e lo si ponga a contatto termico con una sorgente di calore. Se il gas subisce una trasformazione isoterma, esso si espande compiendo un lavoro W, e contemporaneamente assorbe un calore Q dalla sorgente. Poiché la trasformazione è isoterma, l'energia interna U è costante, per cui ΔU = 0 e si ha Q = W. Allora, io ho un'integrale trasformazione di calore in lavoro? No, perchè questo risultato non è l'unico della nostra trasformazione, dato che il gas si è anche espanso. Per riportarlo nelle condizioni di partenza, affinché valga ancora il "solamente" dell'enunciato di Kelvin, occorre raffreddare il gas, ed ecco che salta fuori di nuovo la sorgente fredda.
La più immediata conseguenza, per così dire, antieconomica del Secondo Principio risiede nel fatto che, a causa della presenza della sorgente fredda, non posso estrarre gratuitamente calore dal mare, dall'aria, dalla terra o da chissà quale altra sorgente. Ma non solo.
Def. 5.2: Si dice rendimento di primo principio, o semplicemente rendimento di una macchina termica, il rapporto tra il lavoro W ricavato ad ogni ciclo e il calore Q1 scaricato a ogni ciclo dalla sorgente calda, che viene indicato con il simbolo η:
e, usando la (5.2):
![]()
In generale il rendimento è misurato in percentuale, moltiplicandolo per 100. Per comprendere il significato della def. 5.2 si pensi ad un sarto che acquista 4 metri di stoffa e ne utilizza tre per confezionare un abito, scartandone uno. Qual è l'efficienza del processo di confezionamento del'abito? Ovviamente, è pari al rapporto tra la stoffa utilizzata e quella totale a disposizione del salto, cioè 3/4 = 75 %. Analogamente, il rendimento termico deve essere pari al rapporto tra il calore effettivamente trasformato in lavoro e quello complessivo scaricato dalla sorgente calda, cioè W/Q1.
Esempio 5.1: Una macchina termica scarica ad ogni ciclo 4500 J da una sorgente calda e ne scarica 1800 ad una fredda. Qual è il suo rendimento?
Adoperando la (5.3) otteniamo subito W = Q1 – Q2 = 4500 J – 1800 J = 2700 J, e quindi:
![]()
Il rendimento delle macchine termiche reali in generale è molto bassa. Ad esempio, il rendimento di una locomotiva a vapore non supera il 9 %. Il Ciclo Otto a quattro tempi di una normale automobile bon arriva al 20 %.
Ci viene spontaneo domandare: il rendimento non può essere maggiore del cento per cento, perchè altrimenti la macchina produrrebbe più lavoro di quanto calore assorbe, in contrasto con il Primo Principio (moto perpetuo di prima specie). Ma una macchina può avere esattamente η = 100 %? La risposta è: no. Non può perchè, secondo l'enunciato di Lord Kelvin, ci deve essere per forza una sorgente fredda a cui scaricare una parte del calore, per cui Q1 > 0 e necessariamente W < Q1. Ne segue che η < 100 %. Solo il moto perpetuo di seconda specie potrebbe avere un rendimento tale, e come sappiamo esso è proibito dall'enunciato di Lord Kelvin. Dato che η non può essere pari al 100 %, noi ci chiediamo: qual è il massimo rendimento possibile di una macchina termica, una volta fissate le due temperature tra cui essa lavora?

Nicolas Léonard Sadi Carnot (1796-1832)
.
5.3 Il Ciclo di Carnot
Il problema se lo pose anche il già citato Sadi Carnot, che rispose brillantemente individuando il ciclo che, operando tra de temperature prefissate, raggiunge il massimo rendimento possibile. Questo ciclo è quello raffigurato qui sotto, ed è composto da due isoterme reversibili e da due adiabatiche reversibili. Tale ciclo prende il nome di ciclo di Carnot.
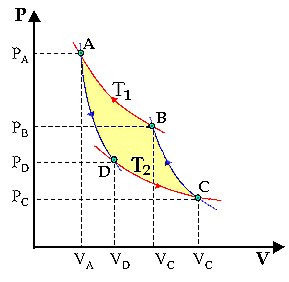
Esso è realizzabile per esempio come illustrato qui sotto. Si pone uno stantuffo contenente gas perfetto a contatto con una sorgente calda a temperatura T1, e si fa compiere al gas una espansione isoterma A→B, facendo innalzare molto lentamente il pistone, in modo che la temperatura del gas non vari apprezzabilmente. Si chiude poi lo stantuffo tra pareti adiabatiche e si lascia espandere il gas senza apporto di calore, ottenendo un'espansione adiabatica B→C. Come si è detto nel § 4.7, nel piano di Clapeyron l'adiabatica è più ripida dell'isoterma, quindi la temperatura cala da T2 a T1. E non c'è da stupirsene, dato che il lavoro è fatto a spese dell'energia interna del fluido. Poi si pone lo stantuffo a contatto con la sorgente fredda a temperatura T1 che gli sottrae calore; con mille precauzioni, la trasformazione è isoterma, e così seguiamo l'espansione isoterma C→D, con diminuzione del volume perchè la pressione aumenta. Infine, si richiude di nuovo lo stantuffo tra pareti adiabatiche e si comprime il tutto senza scambio di calore, aumentando l'energia interna e quindi la temperatura del gas: otteniamo la compressione adiabatica D→A, che fa salire la temperatura da T2 a T1. In tal modo si sono ripristinate le condizioni iniziali, e il ciclo può essere ripetute infinite volte.
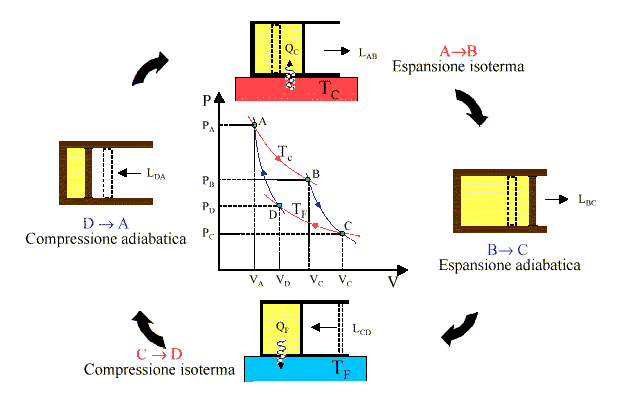
Teorema di Carnot: Il rendimento di un ciclo di Carnot dipende solo dalle temperature T1 e T2 delle due sorgenti, ed è il massimo ottenibile operando tra quelle due temperature.
Dimostrazione della prima parte. Lungo BC e lungo DA non si scambia calore, trattandosi di due adiabatiche; il calore Q1 è interamente assorbito lungo AB, il calore Q2 è interamente scaricato lungo CD. Ora, come si è detto nel § 4.7, si ha:
![]()
![]()
Ora però si può osservare che, siccome AB e CD sono due isoterme, si ha:
PA VA = PB VB
PC VC = PD VD
e, siccome BC e AD sono due adiabatiche:
PA VAγ = PD VDγ
PB VBγ = PC VCγ
Divido membro a membro queste ultime due, ed ho:
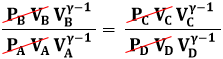
Da cui si ricava:
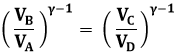
Estraggo la radice di indice γ – 1 ed ho:
Abbiamo così dimostrato il:
Lemma: I prodotti dei volumi dei vertici opposti del ciclo di Carnot sono uguali tra di loro.
Segue allora che:
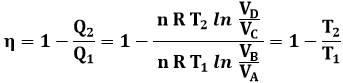
Quindi è vero che il rendimento di Carnot, che noi indicheremo con il simbolo ηc, dipende solo dalle temperature delle due isoterme:
![]()
Vedremo poi un altro modo per calcolare questo rendimento. Ora dimostriamo la seconda parte del teorema di Carnot. Consideriamo un qualunque ciclo reversibile che scambi calore tra le temperature estreme T1 e T2. Come si vede in figura, tale ciclo può essere approssimato con tutta una serie di cicli di Carnot infinitesimi, tali cioè che le loro adiabatiche differiscano di una quantità infinitesima. Il rendimento totale dell'insieme di tutti questi cicli è la media pesata di tutti i rendimenti, usando come pesi le differenze tra le adiabatiche (vedremo più vanti che i pesi sono le differenze di entropia).
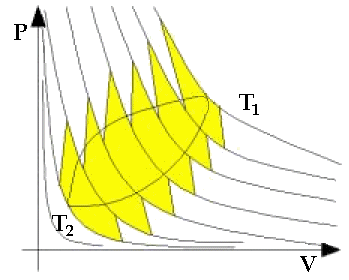
Il fatto però è che, come si vede in figura, la maggior parte di questi cicli ha temperatura massima inferiore a T1 e temperatura minima superiore a T2, per cui il suo rendimento è certamente minore di quello del ciclo di Carnot tra T1 e T2:
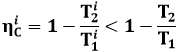
Quindi anche la loro media pesata deve per forza essere inferiore a 1 – T2 / T1. Quanto poi a cicli non reversibili, li decompongo in cicli di Carnot non reversibili, il cui rendimento è certamente peggiore di quello dei corrispondenti cicli di Carnot reversibili, e dunque siamo di nuovo sotto il valore ηc = 1 – T2 / T1.
Esempio 5.2: Una macchina termica funziona tra le temperature estreme di T1 = 427°C e T2 = 27°C. Qual è il suo rendimento massimo?
Naturalmente è quello di Carnot. Siccome le temperature estreme equivalgono a T1 = 700 K e T2 = 300 K, ne risulta:
![]()
Si osservi che, fissata la temperatura della sorgente fredda (ad es., nel caso di una centrale nucleare, quella del mare, di un fiume o dell'atmosfera), il rendimento della macchina di Carnot è tanto migliore quanto maggiore è la temperatura T1, cioè quanto più alta è la temperatura della caldaia, nel caso di una centrale termoelettrica, o del reattore, nel caso di una centrale nucleare. Naturalmente ci sono dei limiti tecnologici all'innalzamento di T1, legati alla resistenza dei materiali (impossibile ad esempio, almeno per ora, ottenere T1 = 10.000 K!), ma ce ne sono anche all'abbassamento di T2: più è fredda la sorgente fredda e più è calda la sorgente calda, meglio funziona il ciclo, ma una caldaia a 2.000°C e un pozzo freddo vicino allo zero assoluto costano, pur essendo tecnicamente ottenibili, e ci costringono a spese che annullano i benefici dell'alto rendimento. Come sempre, i vantaggi ottenuti da una parte si pagano dall'altra.
Def. 5.3: Si dice rendimento di secondo principio ηII (in contrapposizione a η, detto rendimento di primo principio) il rapporto tra il rendimento di primo principio del ciclo reale considerato e quello di un Ciclo di Carnot che opera tra le stesse temperature estreme.
Naturalmente solo il Ciclo di Carnot ha ηII = 100 %. Più è alto ηII, è più noi siamo stati bravi a limitare le irreversibilità del ciclo reale.
Mostriamo ora due esempi di esercizi sui cicli; un terzo lo mostreremo negli Esercizi da risolvere.
Esempio 5.3: Sia il ciclo illustrato nella figura sottostante. Esso è composto da un'isobara (CA), un'isocora (AB) e un'isoterma (BC). Da A a B il volume è costante, quindi per alzare la sua temperatura esso deve assorbire calore dalla sorgente calda; da B a C il fluido si espande in maniera isoterma (cioè con ΔU = 0), e quindi per compiere lavoro deve assorbire ulteriore calore dalla sorgente calda; infine, da C ad A è compresso in maniera isobara, cedendo calore alla sorgente fredda. Ne consegue che il calore è assorbito da A a B e da B a C, ed è ceduto da C ad A. Il gas utilizzato nel ciclo è perfetto e monoatomico, e si ha VC = 4 VA. Intendiamo calcolarne il rendimento di primo e di secondo principio.
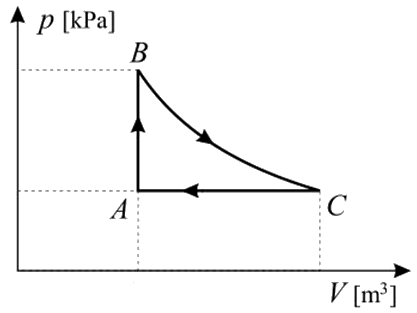
Lungo l'isocora AB si ha W = 0, e quindi:
![]()
Lungo BC, come si è detto, ΔU = 0 e quindi:
![]()
Lungo CA, che è un'isobara, si ha invece:
![]()
![]()
Siccome TB = TC e PC = PA, ne segue che:
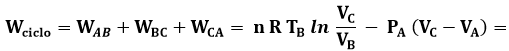
![]()
![]()
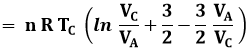
perché PA = PC, e quindi:
![]()
VA/VC prende il nome di rapporto di compressione. Tutto dipende dai dati solo di A e di C, perchè quelli di B si ricavano da questi. Ne segue:
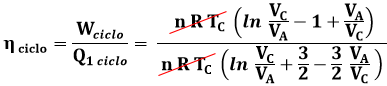
Si noti che il risultato è indipendente dalla pressione!
Siccome nel nostro caso VC = 4 VA, si ottiene:
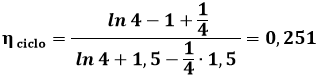
Si osservi che, fra le stesse temperature:
![]()
e quindi si ricava che:
![]()
Esempio 5.4: Sia adesso il nuovo ciclo illustrato nella figura sottostante. Esso è composto da un'isobara (BC), un'isocora (CA) e una trasformazione BC non riconducibile ad una politropica, il cui andamento nel piano di Clapeyron è rettilineo. A lavorare nel ciclo sono 5 moli di gas monoatomico, e si sa che PB = PC = 60 bar, VA = VC = 4 l e VB = 16 l. Anche in questo caso vogliamo calcolarne il rendimento di primo e di secondo principio.
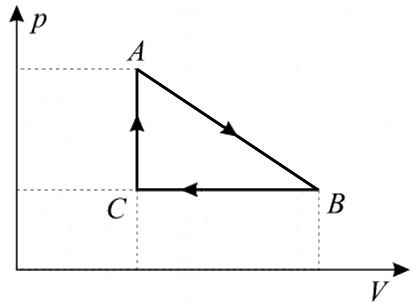
Anzitutto calcoliamo le temperature nei tre vertici del ciclo mediante la (3.3): TA = PA VA / n R = 1924 K; TB = PB VB / n R = 2309 K; TC = PC VC / n R = 577 K.
Partiamo dalla trasformazione BC. Si tratta di una compressione isobara, quindi il lavoro compiuto è negativo. In base alle formule elencate nel § 4.7 si ha:
WBC = P ΔV = 60 x 105 ( 4 x 10–3 – 16 x 10–3 ) = – 72.000 J
QBC = n cP ΔT = 5 x 2,5 x 8,314 ( 577 – 2309 ) = – 180.000 J
ΔUBC = QBC – WBC = – 180.000 + 72.000 = – 108.000 J
Anche il calore è negativo, quindi viene ceduto dal fluido alla sorgente fredda, mentre la variazione di energia interna è negativa perchè la temperatura sta diminuendo.
Passiamo all'isocora CA. Lungo di essa il lavoro è naturalmente nullo, mentre il calore è positivo, e quindi è assorbito dalla sorgente calda:
QCA = n cV ΔT = 5 x 1,5 x 8,314 ( 1924 – 577 ) = + 84.000 J
ΔUCA = QCA – WCA = + 84.000 J
E ora, la trasformazione AB. Il lavoro può essere facilmente determinato calcolando l'area da esso sottesa, che ha la forma di un trapezio:
WAB = ( 200 x 105 + 60 x 105 ) 12 x 10–3 / 2 = 156.000 J
Invece la variazione di energia interna la troviamo con la (4.13):
ΔUAB = n cV ΔT = 5 x 1,5 x 8,314 ( 2309 – 1924 ) = + 24.000 J
E quindi, per il Primo Principio della Termodinamica:
QAB = ΔUAB + WAB = 156.000 J + 24.000 J = + 180.000 J
Anche lungo AB il calore è assorbito dalla sorgente calda, essendo positivo. Possiamo allora calcolare il lavoro prodotto durante un intero ciclo e il calore scaricato dalla sorgente calda:
Wciclo = WAB + WBC + WCA = – 72.000 J + 156.000 J = 84.000 J
Q1 ciclo = QAB + QCA = 180.000 J + 84.000 J = 264.000 J
E di conseguenza:
![]()
![]()
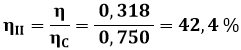
.
5.4 L'enunciato di Clausius
Si è già detto che la natura fissa un verso privilegiato all'evoluzione spontanea dei fenomeni naturali; tale verso non è condizionato dal Primo Principio, per il quale in linea di principio ogni trasformazione è comunque possibile, né dall'enunciato di Kelvin, il quale sembra riguardare unicamente le macchine. Eppure, è facile rendersi conto del fatto che la Natura fissa sempre un verso privilegiato alle trasformazioni. Basti pensare alla reazione chimica:
Ca O + H2O → Ca (OH)2
(produzione dell'idrossido di calcio o calce spenta a partire dall'ossido di calcio o calce viva) Mentre la reazione diretta avviene con grandissima facilità, quella inversa:
Ca (OH)2 → Ca O + H2O
avviene solo attraverso una complicata successione di operazioni che richiedono tempo, fatica, denaro e soprattutto un notevole consumo energetico per far riprendere alle sostanze interagenti le caratteristiche chimico-fisiche iniziali. Idem dicasi per l'evaporazione di un liquido in un recipiente, la diffusione di due gas l'uno nell'altro, la soluzione di un sale nell'acqua, e via discorrendo. Le reazioni o i processi così come sono stati scritti avvengono molto facilmente, mentre le reazioni inverse sono molto difficili da ottenere, e comunque per riuscirci occorre spendere lavoro. Una volta fatta la frittata, le uova e gli altri componenti non si separeranno mai più spontaneamente l'uno dall'altro, così come l'acqua non gelerà spontaneamente senza porla in un frigo, i cocci della finestra rotta da una pallonata non potranno mai ricomporsi da soli, né (purtroppo) alcuno di noi potrà recuperare la giovinezza passata, come sapeva bene Lorenzo il Magnifico (« Quant’è bella giovinezza / che si fugge tuttavia! ») In generale, stabilite le modalità di una trasformazione naturale, è impossibile trovare un processo che possa riportare tutti i sistemi interessati dalla trasformazione allo stato iniziale. La Natura non ritorna mai indietro sui propri passi; o, se si preferisce, il tempo non torna indietro. Il verso naturale nel quale la Natura si muove e si evolve fin dal Big Bang è detto freccia del tempo.
Risulta dunque naturale cercare un principio che esprima nel modo più semplice possibile l'unidirezionalità di tutti i fenomeni sopra citati. Questo lo fa quello che è passato alla storia come il:
SECONDO PRINCIPIO DELLA TERMODINAMICA, ENUNCIATO DI CLAUSIUS: È tecnicamente e teoricamente impossibile realizzare una trasformazione termodinamica il cui unico risultato consiste nella cessione di calore da un corpo più freddo a uno più caldo.
Anche qui bisogna sottotitolare "l'unico risultato": infatti le macchine frigorifere cedono calore da un corpo più freddo (la cella frigorifera) ad uno più caldo (l'atmosfera), ma questo NON è l'unico effetto della trasformazione, perchè il frigorifero consuma anche energia, e quindi non porta avanti un processo spontaneo. Staccando la spina, l'interno del freezer torna spontaneamente a una temperatura pari a quella esterna.

Rudolf Clausius (1822-1888)
Questo enunciato prende il nome dal fisico tedesco Rudolf Clausius (1822-1888), uno dei padri fondatori della Termodinamica, ed appare semplicissimo, anzi banale; eppure, da un punto di vista assiomatico (cioè induttivo), esso è fondamentale per stabilire il verso dei processi e delle reazioni. Inoltre, esso non sembra aver nulla a che fare con il postulato di Kelvin; in altre parole, pare enunciare qualcosa di completamente differente, perchè quello si occupa di macchine e di trasformazione del calore in lavoro, e questo del passaggio spontaneo o meno di calore. Eppure, vi assicuro che si tratta dello stesso Principio, nonostante Kelvin non sembri essersi curato del concetto di irreversibilità, e Clausius sembri aver ignorato le macchine termiche. Ed ora ve lo dimostrerò.
Procediamo per assurdo. Supponiamo che l'enunciato di Kelvin non sia valido, cioè che esista un ciclo termodinamico in grado di trasformare integralmente in lavoro il calore estratto da una sorgente. Ad esempio, come si vede qui sotto, estrae 1000 J di calore da una sorgente calda (in arancione) e li converte integralmente in 1000 J di lavoro. Ma allora io potrei utilizzare questo lavoro per azionare un mulinello di Joule, che lo dissipa sotto forma di attrito in una sorgente a temperatura maggiore della precedente (in rosso). In tal modo, avrei realizzato una trasformazione il cui unico risultato è quello di trasferire 1000 J di calore da una sorgente di calore ad un'altra a temperatura maggiore, e così anche l'enunciato di Clausius cessa di essere valido. Negare l'enunciato di Kelvin equivale a negare anche l'enunciato di Clausius.
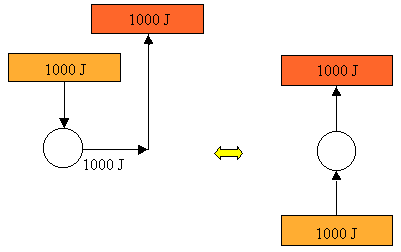
Analogamente, supponiamo per assurdo che Clausius abbia torto, e che sia possibile realizzare un ciclo che assorbe calore a temperatura T2 (in azzurro) e lo cede, senza alcun consumo di lavoro, ad una sorgente a temperatura T1 > T2 (in arancione). Allora io potrei accoppiarla ad una macchina termica ordinaria, che assorbe 1300 J dalla sorgente a temperatura T1, scarica 300 J alla sorgente a temperatura T2 e produce un lavoro di 1000 J. La macchina che dà torto a Clausius potrebbe prelevare i 300 J scaricati alla sorgente fredda e riportarli alla sorgente calda. Questa vedrebbe così il suo bilancio energetico in parità; in tal modo però abbiamo realizzato una macchina il cui solo risultato è quello di prelevare 1300 300 = 1000 J da una sorgente di calore e trasformarli integralmente in lavoro meccanico. E così, anche Kelvin viene messo in soffitta: negare l'enunciato di Clausius equivale a negare anche l'enunciato di Kelvin.
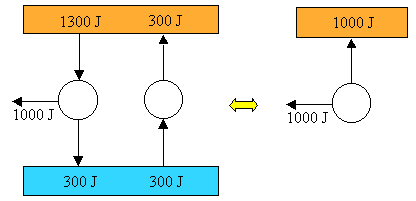
Come si vede, i due enunciati risultano perfettamente equivalenti, perchè l'uno implica l'altro. Non si tratta dunque di due diversi Principi della Termodinamica, ma di due diversi modi di enunciare lo stesso Principio!
.
5.5 La macchina frigorifera
Dedichiamo un paragrafo anche a quello che è diventato uno degli elettrodomestici più comuni nelle nostre case: il frigorifero. Fin dalla preistoria, conservare il cibo per i periodi in cui esso scarseggiava fu una necessità impellente; questo risultato veniva un tempo ottenuto con l'uso di spezie, oppure con la refrigerazione per mezzo di neve e ghiaccio, raccolti in alta montagna e poi trasportati nelle città. Già nel Rinascimento si diffusero le ghiacciaie, mobili termicamente isolati (per mezzo di paglia, foglie secche o stracci) in grado di conservare il ghiaccio al loro interno. A quest'epoca, però, nessuno era ancora in grado di refrigerare un ambiente. La prima macchina refrigerante fu messa a punto nel 1748 dallo scozzese William Cullen (1710-1790), mentre nel 1805 Oliver Evans (1755-1819) progettò il primo frigorifero basato su un liquido che evaporava. Nel 1834 l'americano Jacob Perkins (1766-1849) realizzò il primo frigorifero domestico con sistema di compressione, mentre nel 1857 l'australiano James Harrison (1816-1893) inventò la prima macchina di refrigerazione destinata alla conservazione dei prodotti industriali, utilizzata per la prima volta nelle industrie di Geelong (Victoria). Nel 1859 il francese Ferdinand Philippe Carré (1824-1900) inventò la prima macchina refrigerante basata sull'utilizzo dell'ammoniaca come liquido refrigerante, e nel 1876 il francese Louis Charles Tellier (1828-1913) realizzò il primo impianto frigorifero su un piroscafo, che trasportò in Francia un carico di carne macellata in Argentina, dopo un viaggio di 105 giorni. Il primo frigorifero domestico venne messo in vendita nel 1913; ma solo dopo la Seconda Guerra Mondiale, il boom economico legato alla ricostruzione fece sì che le grandi aziende metalmeccaniche cominciassero a costruire in serie apparecchi frigoriferi destinati all'uso domestico, che all'inizio erano molto costosi, ma che in seguito raggiunsero prezzi accessibili man mano che si diffondevano in ogni casa. Ma non fatevi illusioni: gran parte delle famiglie del Terzo e Quarto Mondo è ancora ben lontana dal potersi permettere un frigorifero in cucina, ed esso resta ancora un privilegio della nostra opulenta civiltà occidentale.
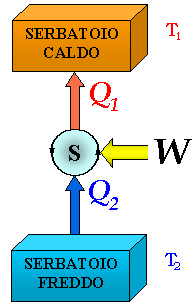
Il frigorifero compie un lavoro negativo, cioè assorbe energia dall'esterno, estrae calore da una sorgente fredda (la cella frigorifera) e lo cede a una sorgente calda, cioè l'ambiente esterno, sfruttando un ciclo termodinamico inverso, cioè percorso in senso antiorario nel Piano di Clapeyron. Il calore che esso riversa nella stanza in cui è posizionato è maggiore del calore prelevato al suo interno, perchè il frigorifero cede all'ambiente esterno sia il calore estratto dalla sorgente fredda, sia un'ulteriore quantità di calore equivalente al lavoro W compiuto dal suo motore. È per questo che un frigorifero che funziona a sportello aperto non solo non raffredda la stanza in cui si trova, ma anzi la scalda!
Quanto è efficiente un ciclo frigorifero? Lo misura il cosiddetto coefficiente di prestazione o COP (dall'inglese Coefficient Of Performance), dato dal rapporto tra il calore estratto dalla sorgente fredda e il lavoro compiuto a questo scopo:
Mentre il rendimento di un ciclo diretto è sempre minore di 1, il COP può essere anche maggiore di 1; anzi, maggiore è, meglio è, perchè alti valori del coefficiente di prestazione sono indicativi di un frigorifero che richiede poca energia elettrica per sottrarre una grande quantità di calore al suo interno. Tipicamente il COP assume valori compresi fra 2 e 6.
Esempio 5.5: Il motore di un frigorifero assorbe 6000 J di energia dalla rete elettrica per estrarre 25000 J di calore dalla cella di un frigorifero. Quanto vale il suo COP?
Utilizzando la (5.6) avremo:
![]()
Ma come funziona, un frigorifero? Esso è costituito da un ambiente chiuso, che noi dobbiamo raffreddare, e da un lungo tubo nel quale circola del vapore. Il tubo è collegato ad un compressore, passa tutt'intorno alla cella frigorifera e poi emerge e forma una serpentina a contatto con l'aria esterna. Il compressore ha lo scopo di comprimere il fluido fino a farlo liquefare; questo fa aumentare la temperatura del fluido. La serpentina esterna ovviamente permette il passaggio di calore dal fluido all'atmosfera esterna. Il tubo è dotato di una valvola ad espansione posta nel punto in cui esso penetra nel frigorifero. Quando il liquido attraversa la valvola ed entra nel frigorifero, esso non è più compresso e torna allo stato di vapore. Nel corso di questa trasformazione, assorbe calore dall'interno del frigorifero, che si raffredda. La serpentina interna permette così il passaggio di calore dall'interno del frigorifero al fluido. Infine il vapore torna all'esterno, viene compresso di nuovo e il ciclo riprende daccapo.
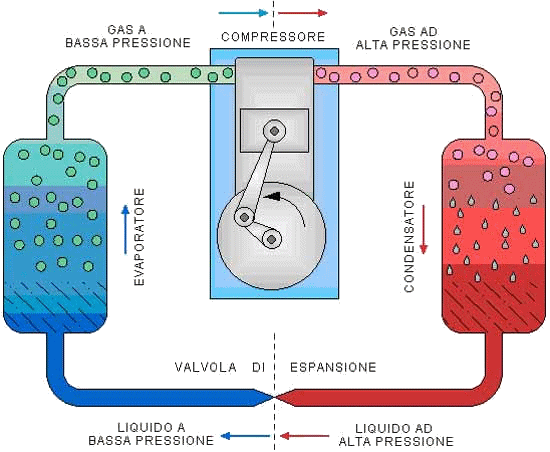
Il fluido da usare nel frigorifero deve avere la proprietà di condensare a pressione relativamente bassa anche a temperatura ambiente. Come si è detto sopra, inizialmente a questo scopo era usata l'ammoniaca, che liquefa a 15°C alla pressione di 7 atmosfere. Essa era però poco adatta allo scopo, in quanto ha lo svantaggio di essere assai corrosiva, e così fu sostituita nel 1931 dal freon o dicloro-difluorometano, della famiglia dei clorofluorocarburi, idrocarburi contenenti cloro molto più efficienti e meno corrosivi: esso liquefa a 20°C se compresso a 5,6 atmosfere. Nel 1974 però due scienziati americani, Frank Sherwood Rowland (1927-2012) e Mario José Molina Henríquez (1943-), Premi Nobel per la chimica nel 1995 insieme a Paul Crutzen, dimostrarono che il freon è dannosissimo per l'ambiente, distruggendo lo strato d'ozono nell'atmosfera che ci protegge dai raggi ultravioletti del Sole; per questo, dopo una lunga battaglia da parte degli ambientalisti, il freon fu messo al bando nel 1990 dal Protocollo di Montreal e sostituito con fluidi con minore impatto ambientale, come l'isobutano (che però è molto infiammabile).
Non si può concludere questo paragrafo senza un accenno ai condizionatori d'aria. Anche il condizionamento dell'aria è un problema vecchio quanto la civiltà umana, poiché ridurre il caldo e l'umidità è sempre stato l'obiettivo principale per rendere confortevole uno spazio abitato. Chi è stato d'estate nelle aree desertiche dell'altopiano iranico ha un'idea delle temperature che vi si raggiungono: un caldo atroce, che ha spinto gli abitanti delle molte città carovaniere disseminate nelle oasi lungo la via della seta a cercare disperatamente un po' di frescura. Il risultato è stata l'invenzione delle cosiddette "torri del vento", i più antichi condizionatori del mondo. Si tratta di torri costruite in argilla e paglia, che svettano nei cieli dell'Iran e sono in grado di catturare i venti caldissimi, incanalarli al loro interno e raffreddarli a contatto con l'acqua conservata in grandi cisterne sotterranee costruite alla loro base. Questo sistema di condizionamento, già noto agli antichi Egizi, è così efficace e poco costoso da essere tuttora in uso; oggi le torri del vento di Yazd, visibili qui sotto, sono patrimonio mondiale dell'UNESCO.

Questo problema era sentito anche in Cina: pare che Ding Huan, inventore cinese del secondo secolo d.C., vissuto al tempo della dinastia Han, avesse inventato un ventilatore rotante con sette ruote di tre metri di diametro, messa in moto manualmente da schiavi, per condizionare l'aria. Tra gli altri, affrontarono il problema di condizionare l'aria anche Leonardo da Vinci e Benjamin Franklin, ma il primo apparecchio per il raffreddamento climatico dell'aria fu brevettato nel 1886 dallo scienziato afroamericano Lewis Latimer (1848-1928); un ulteriore contributo fu dato nel 1902 dai progetti di Willis Haviland Carrier (1876-1950), che riuscì a risolvere il problema del controllo dell'umidità dell'aria in una tipografia di Brooklyn, dove la carta era inutilizzabile a causa dell'eccessiva umidità nell'aria, perché raggrinziva. Nel 1945, infine, l'americano Robert Sherman inventò un condizionatore d'aria portatile da porre sulla finestra, che raffreddava, riscaldava, umidificava, deumidificava e filtrava l'aria: era iniziata l'era del condizionamento domestico.
Un condizionatore è un ciclo frigorifero il cui scopo è quello di raffreddare non l'interno di un elettrodomestico, ma l'intero appartamento in cui esso si trova. Onde evitare di ottenere l'effetto opposto, il motore viene posto all'esterno dell'appartamento e riscalda l'aria della città circostante. Quando questa soluzione non è possibile o conveniente, il motore è posto in un ambiente isolato dall'appartamento e raffreddato con acqua o aria o acqua provenienti dall'esterno, come avviene nel motore di un'automobile. Invece si dice pompa di calore un ciclo frigorifero il cui scopo è quello non di raffreddare un ambiente freddo, come nel caso del condizionatore, bensì di riscaldare un ambiente caldo. In questo caso il rapporto Q1/W è detto coefficiente di guadagno K della pompa di calore. Una pompa di calore con un coefficiente di guadagno pari o superiore a 5 può insufflare in un appartamento più di 5 J di calore per ogni Joule pagato con la bolletta! Infine, la pompa di calore geotermica è un impianto di climatizzazione degli edifici che sfrutta lo scambio termico con il sottosuolo per mezzo di una pompa di calore; questo impianto fu inventato nel 1912 dall'ingegnere svizzero Heinrich Zoelly (1862–1937).
.
5.6 Il Terzo Principio della Termodinamica
Quanto detto fin qui ci spinge ad ulteriori considerazioni. Come si può facilmente osservare, per un Ciclo di Carnot i valori di ηC sono compresi tra due estremi: se T1 = T2 , ηC = 0; se T2 = 0, ηC = 1. Quest'ultima condizione, a parte T1 → ∞, manifestamente assurda, è l'unica che garantisca di avere ηC = 1. Per definizione di rendimento, però, ηC = 1 – Q2 / Q1; tale valore è pari ad uno solo se Q2 = 0, ma questo è proibito dall'enunciato di Kelvin del Secondo Principio. Siccome è impossibile non solo avere η > 1, ma anche solo η = 1, e ne deduce che è anche impossibile che T2 raggiunga lo zero assoluto.
Di conseguenza non solo non si può scendere sotto lo zero della Scala Kelvin, ma non lo si può neppure raggiungere, esattamente come non solo non si può viaggiare più veloci della luce, ma non si può nemmeno raggiungere tale velocità, a meno di spendere un'energia infinita. Questo ci consente di enunciare quello che è passato alla storia con il nome di...
TERZO PRINCIPIO DELLA TERMODINAMICA: Non è possibile realizzare un processo che porti un sistema allo zero assoluto con un numero FINITO di trasformazioni.
Esso prende anche il nome di Principio di Nernst, in onore del suo ideatore, il chimico tedesco Walther Hermann Nernst (1864-1941), che lo enunciò nel 1912; in realtà il termine "Principio" usato in questo caso è improprio, perchè come abbiamo visto esso è deducibile dal Secondo Principio, e di conseguenza è più corretto parlare di "Teorema di Nernst", anche se per motivi storici si continua ad usare il termine "Principio".

Walther Hermann Nernst (1864-1941)
Il Terzo Principio ci dice, senza troppi giri di parole, che lo zero assoluto è il limite inferiore di tutte le temperature, così come la velocità della luce è il limite superiore di tutte le velocità. Nessun limite superiore è invece fissato per le temperature da nessuno dei Principi della Termodinamica. Vale la pena dunque di addentrarci per un po' nella Fisica delle basse temperature.
La temperatura minima mai registrata in Italia è pari a – 49,6°C (223,6 K), ed stata registrata il 10 febbraio 2013 a quota 2.607 in una dolina di Busa Fradusta nel complesso delle Pale di San Martino, al confine tra Veneto e Trentino. In una località di pianura invece il record spetta ad Anzola dell'Emilia (in provincia di Bologna), dove il 15 febbraio 1956 sono stati registrati – 26,2°C (247,0 K ). Sull'intera superficie terrestre invece la temperatura più bassa mai misurata corrisponde a – 89,2°C (184,0 K) ed è stata registrata il 21 luglio 1983 in Antartide nella base scientifica sovietica di Vostok, alla quota di 3420 m. Ma non basta: il 10 agosto 2010 il satellite Landsat 8 ha misurato una temperatura di – 93,2°C (180,0 K)sempre in Antartide, lungo il crinale tra il Dome Argus e il Dome Fuji alla quota di 3900 m. Per quanto riguarda i centri abitati, il 6 febbraio 1933 nel villaggio siberiano di Ojmjakon fu registrata una temperatura di – 67,8°C (205,4 K). Le superfici di altri mondi del Sistema Solare possono raggiungere temperature molto inferiori. La Luna diventa caldissima nella metà esposta alla luce del Sole, ma subisce un rapido crollo della temperatura quando arriva la notte, perchè non ha atmosfera per trattenere il calore. Ogni punto della superficie lunare resta immerso nella notte per due settimane, e così la temperatura lunare, poco prima dell'alba, scende fino a – 173°C (100 K), considerevolmente al di sotto del minimo registrato in Antartide.
Il pianeta Mercurio è molto più vicino al Sole della Luna, per cui può raggiungere temperature assai più alta durante il giorno, ma ha una sei volte più lunga della notte lunare, e quindi la sua temperatura scende ancora di più, nonostante la vicinanza al Sole. Poco prima che il gigantesco Sole di Mercurio sorga sopra l'orizzonte, la temperatura sulla superficie del primo dei pianeti può scendere fino a – 183°C (90 K). Marte è più lontano dal Sole di Mercurio e della Terra, ma la sua notte è solo di pochi minuti più lunga di quella terrestre, e non raggiunge i minimi registrati sulla Luna e su Mercurio: il minimo registrato è di – 140°C (133 K). I giganti gassosi del Sistema Solare, soprattutto quelli esterni, sono ancora più freddi, visto che il riscaldamento da arte del Sole diminuisce con il quadrato della distanza da esso. Urano è circa 20 volte più lontano dal Sole rispetto a noi, e dunque riceve solo 1/400 del calore che noi riceviamo dal Sole; per questo la temperatura minima sulla sua superfiche è di – 214°C (59 K). Nettuno è 30 volte più lontano della Terra, e riceve solo 1/900 del calore che giunge sulla Terra; nessuna sorpresa che alla sommità delle sue nubi la temperatura scenda fino a – 223°C (50 K). Il pianeta nano Plutone è in media 40 volte più lontano di noi dal Sole, su di esso arriva solo 1/1600 della luce solare che raggiunge noi, e su di esso la temperatura minima è di – 233°C (40 K). 90377 Sedna, l'oggetto del Sistema Solare più lontano dal Sole a noi noto (il perielio è a 11 miliardi di km dalla nostra stella, l'afelio si trova addirittura a 5 giorni luce da essa!), potrebbe avere una temperatura superficiale di – 261°C (12 K). Infine, tutto l'universo è pervaso da una radiazione a microonde detta radiazione cosmica di fondo, fatta di microonde, che rappresenta l'eco residuo del Big Bang. Scoperta nel 1964 dagli statunitensi Arno Penzias (1933-) e Robert Woodrow Wilson (1936-), essa arriva con la stessa intensità da tutte le direzioni, e corrisponde a una radiazione di corpo nero alla temperatura di 2,726 K (circa – 270°C). Questa rappresenta a tutti gli effetti della temperatura media dell'universo, perchè qualunque oggetto del cosmo, per quanto non produca energia e per quanto sia lontano da qualunque stella, assorbe sempre abbastanza microonde per raggiungere i 2,726 K.

La superficie di Plutone ripresa dalla sonda New Horizons il 14 luglio 2015
Si può scendere sotto questa temperatura? Si può rispondere positivamente a tale domanda solo intraprendendo la via della ricerca di metodi di refrigerazione artificiale. Un pioniere in questo campo fu il grande fisico britannico Michael Faraday (1791-1867), vero e proprio esempio di self made man, il quale studiò a fondo il problema della liquefazione dei gas conosciuti alla sua epoca, e che in natura spontaneamente non liquefano. Nel 1823 Faraday utilizzò un tubo di vetro piegato a gomito nel cui fondo chiuse una sostanza che, riscaldata, avrebbe liberato del cloro, poi sigillò estremità opposta del tubo e introdusse quest'ultima nel ghiaccio, e l'altra nell'acqua calda. Il cloro veniva liberato in quantità crescente all'estremità riscaldata, e quindi aumentava la sua pressione. Sotto l'effetto combinato dell'abbassamento della temperatura e dell'aumento della pressione, il cloro passò allo stato liquido. Faraday era sceso a 238,5 K, cioè a – 34,5°C. Non un gran che rispetto alla radiazione cosmica di fondo, ma certo un grande successo per i tempi, visto che ai primi dell'Ottocento il gas cloro era dai più considerato incondensabile! Nel 1835 il chimico francese Adrien-Jean-Pierre Thilorier (1790-1844) usò il metodo di Faraday (con tubi di metallo anziché di vetro, onde reggere pressioni assai maggiori) per liquefare l'anidride carbonica, e poi addirittura per congelarla. Egli scoprì che l'anidride carbonica solida non fonde ma sublima, passando direttamente allo stato gassoso, ed è per questo che la chiamò ghiaccio secco, nome con cui è noto tuttora. Il punto di sublimazione dell'anidride carbonica a temperatura ambiente è di 194,5 K (– 78,7°C): ancora al di sopra della minima temperatura mai registrata sulla Terra. Thilorier però si spinse oltre, mescolando all'anidride carbonica solida dell'etere dietilico (il noto anestetico) che restava liquido anche alle temperature a cui la CO2 gelava; facendo evaporare l'etere, come ben sappiamo la temperatura della miscela si abbassava ancor più, e Thilorier raggiunse i 163 K (– 110°C), infrangendo la barriera rappresentata dalle temperature dell'Antartide. Per la prima volta nella storia della scienza, la temperatura più bassa della Terra era quella ottenuta in un laboratorio.
A quella temperatura molti gas liquefacevano, ma non tutti. Infatti, molti gas hanno una temperatura critica (sotto la quale non possono essere liquefatti per sola compressione) inferiore ai 163 K. Tra questi vi erano l'ossigeno, l'azoto e l'ossido di carbonio. Per liquefare questi gas occorreva dunque scendere a temperature ancora più basse; per questo, il chimico francese Louis Paul Cailletet (1832-1913) utilizzò l'espansione libera di Joule: un gas, fatto espandere in condizioni adiabatiche, deve necessariamente raffreddarsi, visto che la sua energia interna diminuisce. Grazie a tale procedimento, nel 1877 Cailletet riuscì a liquefare l'ossigeno alla temperatura di 133 K (– 140°C) e alla pressione di parecchie centinaia di atmosfere. Nel 1883 i chimici polacchi Zygmunt Florenty Wróblewski (1845-1888) e Karol Stanislaw Olszewski (1846-1915) riuscirono a produrre grandi quantità di ossigeno liquido, rendendolo disponibile per applicazioni industriali. Wróblewski morì prematuramente in un incendio scoppiato accidentalmente nel suo laboratorio, ma Olszewski proseguì gli studi da solo e liquefece anche azoto liquido e ossido di carbonio liquido in quantità. Risultò così che l'ossigeno a pressione ambiente ha un punto di ebollizione di 90,2 K (– 183,0°C), l'argo di 87,5 K (– 185,7°C), l'ossido di carbonio di 81,6 K (– 191,6°C) e l'azoto di 77,3 K (– 195,9°C). Alla temperatura di 83,9 K (– 189,3°C) addirittura l'argo congelò.

Azoto liquido, foto di Charles D Winters
A questo punto il prossimo obiettivo diventava liquefare l'idrogeno, che si ostinava a restare gassoso anche a quelle temperature davvero basse. Fu il chimico scozzese James Dewar (1842-1923), uno degli inventori del calorimetro, a rendersi conto che l'espansione libera di Joule non poteva liquefare l'idrogeno se non sotto la temperatura di 190 K, e nel 1898 riuscì nell'impresa, scoprendo che ha un punto di ebollizione di 20,3 K (– 252,9°C). Ormai si erano raggiunte temperature inferiori a quelle di tutti i pianeti del Sistema Solare. Alle temperature a cui liquefa l'idrogeno, tutte le altre sostanze note eccettuata l'elio sono solide: l'ossido di carbonio congela a 74 K (– 199,2°C), l'azoto a 63,3 K (– 209,9°C), l'ossigeno a 54,7 K (– 218,5°C), il neon a 24,5 K (– 248,7°C). L'elio non solo a queste temperature non congela, ma non liquefa neppure, rimanendo incredibilmente allo stato gassoso. Il primo a liquefare l'elio fu il fisico olandese Heike Kamerlingh Onnes (1853-1926), del quale abbiamo parlato nel § 4.8, che nel 1908 prima immerse l'elio gassoso in un bagno di idrogeno liquido, e poi lo sottopose ad espansione libera di Joule facendolo scendere fino alla temperatura di condensazione di 4,24 K (– 268,91°C): a un soffio, ormai, dalla temperatura media della radiazione cosmica di fondo. L'elio (scoperto nel 1868 nello spettro della luce solare, da cui il nome) possiede il più basso punto di ebollizione tra tutti gli elementi, ed è l'unico liquido che non può essere solidificato abbassandone solo la temperatura; rimane liquido fino allo zero assoluto a pressione standard (si può solidificare solo aumentando la pressione). Il primo a ottenere la solidificazione dell'elio nel 1926 fu l'olandese Willem Hendrik Keesom (1876-1956), discepolo di Kamerlingh Onnes, pochi mesi dopo la morte di quest'ultimo: Keesom aveva raggiunto l'incredibile temperatura di 0,95 K (– 272,20°C) e la pressione di 2,5 MegaPascal.
Quando furono prodotte queste temperature, fu chiaro che l'umanità aveva compiuto un'impresa straordinaria: a meno che esistano altre civiltà extraterrestri che stanno portando avanti una corsa verso le temperature più basse possibili, Kamerlingh Onnes, Keesom e colleghi hanno ottenuto un record universale, raggiungendo le temperature più basse dell'intero creato! Tuttavia, la corsa non si fermò a questo punto. Perché? Perchè gli scienziati avevano scoperto che, in prossimità dello zero assoluto, la materia comincia a comportarsi in maniera strana. Heike Kamerlingh Onnes nel 1911 scoprì il fenomeno della superconduttività: a 4,2 K il mercurio perde tutta la sua resistenza elettrica, e analogamente si comportano tutte le altre sostanze conosciute, una volta portate a temperature bassissime. Nel 1957 gli statunitensi John Bardeen (1908-1991), Leon Neil Cooper (1930-) e John Robert Schrieffer (1931-) dimostrarono che la superconduttività è un fenomeno quantistico, conseguenza del cosiddetto effetto tunnel, e per questo ricevettero nel 1972 il Premio Nobel per la Fisica. Nel 1937 Pëtr Leonidovič Kapica (1894-1984), John Frank Allen (1908-2001) e Don Misener scoprirono la superfluidità, cioè l'assenza totale di viscosità: l'elio liquido può scorrere infinitamente senza attrito in un percorso chiuso e, se posto in una provetta, può addirittura uscire da essa, letteralmente "arrampicandosi" lungo le sue pareti! Nel 1924 invece Albert Einstein e il fisico indiano Satyendra Nath Bose (1894-1974) osservarono che, al di sotto di una certa temperatura, le molecole condensano in assenza di forze attrattive, e in un articolo scrissero: « Nella teoria del gas ideale si richiede in modo evidente che volume e temperatura di una quantità di gas possano essere dati arbitrariamente. Mediante la teoria si determina quindi l'energia e la pressione del gas. Ma lo studio delle equazioni di stato [...] mostra che se il numero N di molecole e la temperatura T sono dati, il volume non può essere arbitrariamente piccolo. [...] Che succede allora se la densità N/V della sostanza aumenta a questa temperatura, ad esempio mediante una compressione isoterma? Affermo che in questo caso, al crescere della densità, un numero di molecole crescente cade nello stato fondamentale la cui energia cinetica è nulla). [...] Si realizza una separazione: una parte [delle molecole] condensa, le rimanenti rimangono a far parte di un gas perfetto saturo. » Questo fenomeno è chiamato condensazione di Bose-Einstein. In pratica, a circa 3 K si ha una transizione di fase verso un nuovo stato della materia chiamato condensato di Bose-Einstein, nel quale gruppi di bosoni (come ad esempio il deuterio, isotopo dell’idrogeno) si uniscono a formare un condensato che si comporta come fosse una singola particella, essendosi perse le identità delle singole particelle. Questo stato della materia non esiste in natura, perché le temperature a cui avviene la transizione non si realizzano da nessuna parte nell'universo. Il condensato di Bose-Einstein rimase una speculazione teorica fino al 1995, quando Eric Allin Cornell (1961-) e Carl Edwin Wieman (1951-) isolarono in laboratorio un condensato di Bose-Einstein di atomi di rubidio, impresa per la quale vinsero il Premio Nobel nel 2001.
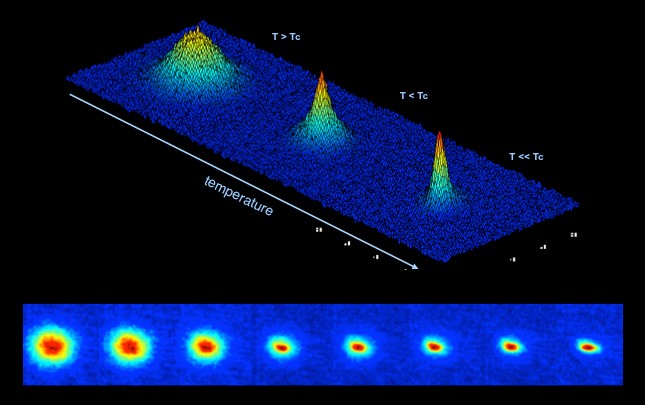
Rappresentazione della formazione di un condensato di Bose-Einstein (foto NASA)
Grazie ai progressi della Fisica del Novecento, fu chiaro che le anomale proprietà degli atomi in vicinanza dello zero assoluto hanno luogo perchè in quelle condizioni gli effetti quantistici, che alle temperature ordinarie non si osservano a causa delle fluttuazioni termiche, predominano su quelli classici. Lo stesso Terzo Principio della Termodinamica può essere visto come una conseguenza delle scoperte della Fisica Moderna: infatti nel 1927 il famoso fisico tedesco Werner Karl Heisenberg (1901-1976) enunciò il celeberrimo Principio di Indeterminazione, secondo il quale la posizione e la quantità di moto di una particella, così come l'energia e la durata di una certa trasformazione, non possono mai essere conosciute simultaneamente con la stessa precisione. Di conseguenza l'energia non può mai essere pari a zero, altrimenti la conosceremmo con precisione assoluta, in contrasto con il Principio di Indeterminazione. E siccome per la (4.13) la temperatura assoluta è pari a zero Kelvin solo quando l'energia interna è zero, esattamente allo zero assoluto non si potrà pervenire mai.
Proprio per studiare i comportamenti assolutamente bizzarri della materia presso lo zero assoluto, come quelli sopra descritti, i fisici continuarono instancabilmente a cercare di raggiungere temperature sempre più basse. La tecnica di lasciar espandere adiabaticamente i gas ed evaporare i liquidi giunse a un vicolo cieco negli anni Venti del secolo scorso, intorno alla temperatura di 0,5 K: era necessario battere strade nuove. Nel 1926 il chimico olandese Peter Joseph William Debye (1884-1966) e il chimico statunitense William Francis Giauque (1895-1982), indipendentemente l'uno dall'altro, proposero una nuova tecnica. In alcune sostanze, come il solfato idrato di gadolinio, gli atomi di questo metallo agiscono come minuscoli dipoli magnetici; in presenza di un forte campo magnetico, tutti i dipoli magnetici si allineano nella stessa direzione, e la sostanza risulta magnetizzata. Se il campo magnetico viene annullato, gli atomi tornano a muoversi a casaccio, e il solfato idrato di gadolinio perde ogni proprietà magnetica. Ma i momenti magnetici degli atomi, muovendosi in modo caotico, assorbono calore e, se sono isolati dal mondo esterno, devono assorbirlo dalla sostanza stessa, per modo che la sua temperatura si abbassa. Quindi, se il solfato idrato di gadolinio viene magnetizzato e poi raffreddato alla temperatura più bassa possibile, per poi rimuovere il campo magnetico, la temperatura si abbassa ancora di più: questa tecnica prende il nome di demagnetizzazione adiabatica. Nel 1933 Giauque ottenne con questa tecnica una temperatura di 0,25 K. Nello stesso anno altri chimici usarono il fluoruro di cerio per ottenere una temperatura di 0,13 K e l'etilsolfato di cerio per arrivare a 0,0185 K. In seguito la demagnetizzazione adiabatica permise di scendere fino a 0,003 K.

William Francis Giauque (1895-1982)
Nel 1962 il fisico tedesco naturalizzato britannico Heinz London (1907-1970) fece notare che gli atomi di elio-3 (isotopo raro dell'elio), essendo più leggeri di quelli di elio-4 (l'isotopo di elio più diffuso in natura), si muovono più rapidamente, e contribuiscono in modo rilevante alla temperatura della miscela naturale di elio. A temperature estremamente basse, elio-3 ed elio-4 non si mescolano perfettamente, ed usando uno strumento chiamato refrigeratore a diluizione è possibile estrarre il primo isotopo dalla miscela, sottraendo ad essa gran parte del calore e quindi abbassando ancor più la temperatura di quanto rimane. La combinazione della demagnetizzazione adiabatica e del refrigeratore a diluizione ha permesso di raggiungere la temperatura di 0,00002 K, a un cinquantamillesimo di Kelvin dallo zero assoluto.
Una variante della demagnetizzazione adiabatica è la demagnetizzazione adiabatica nucleare, che segue lo stesso principio, ma in questo caso la potenza refrigerante viene fornita dai momenti magnetici nucleari, e non dal momento magnetico atomico. Poiché questi momenti di dipolo sono molto più piccoli, è più difficile allinearli. Questo consente una maggiore potenza di refrigerazione, con il quale usando il PrNi5 fu raggiunta una temperatura di 1 microKelvin (0,000001 K), ma a prezzo di usare campi magnetici molto più intensi.
Ma non basta. Nel settembre 2003 alcuni fisici del Massachusetts Institute of Technology guidati dal Premio Nobel 2001 Wolfgang Ketterle (1957-) sono andati ancora oltre, ed hanno raffreddato un gas di sodio fino a mezzo miliardesimo di grado sopra lo zero assoluto. Si tratta della prima volta in cui un gas è stato raffreddato al di sotto di un nanokelvin! Per raggiungere questa temperatura da record, gli scienziati hanno ideato un nuovo modo di confinare gli atomi in una "trappola gravito-magnetica", nella quale i campi magnetici agiscono insieme alle forze gravitazionali per impedire agli atomi di fuoriuscire. I ricercatori si attendono che a temperature così basse cambi il modo in cui gli atomi interagiscono con le superfici e il loro movimento quando sono confinati in un canale molto stretto. Questi gas potrebbero portare a grandi miglioramenti nelle misure di precisione, consentendo di ottenere orologi atomici migliori e sensori di gravità e rotazione più potenti.
Infine, è in fase di sviluppo il cosiddetto Cold Atom Laboratory (CAL), uno strumento sperimentale in fase di sviluppo che verrà lanciato sulla Stazione Spaziale Internazionale nel giugno 2017. Lo strumento creerà condizioni di freddo estremo nell'ambiente di microgravità della ISS, il che porterà alla formazione di condensati di Bose-Einstein decisamente più freddi rispetto a quelli ottenibili nei laboratori sulla Terra. Secondo i calcoli, in un laboratorio spaziale in condizioni di quasi totale assenza di gravità si dovrebbe poter raggiungere una temperatura dell'ordine di un picoKelvin (un millesimo di miliardesimo di Kelvin sopra lo zero assoluto), il che potrebbe portare all'esplorazione di fenomeni quantistici sconosciuti e potrebbe consentire di testare alcune leggi fondamentali della fisica. Potremmo persino avere indicazioni sulle caratteristiche della fantomatica energia oscura. Ma io sono sicuro che la corsa al record di temperatura più bassa mai raggiunta non si fermerà certo qui.

.
C'è però un fatto: finora, nessuno dei due enunciati del Secondo Principio della Termodinamica ha una veste matematica. Noi gliela daremo introducendo il concetto di entropia Per sapere come, cliccate qui e proseguite il viaggio in mia compagnia! Per tornare all'indice, invece, il link è questo.
![]()