Appendice: la propagazione del calore

.

A.1  Fourier e la conduzione del calore

Vorrei chiudere questo ipertesto con alcuni approfondimenti sulla propagazione del calore, a livello anche più avanzato di quello liceale. Questa Appendice è dunque destinata a chi possiede non solo le basi, ma anche conoscenze approfondite di Analisi Matematica. La trattazione che svolgeremo qui sotto la dobbiamo ad uno dei più grandi matematici mai vissuti, Jean Baptiste Joseph Fourier.

Nato ad Auxerre il 21 marzo 1768 da una famiglia modesta, rimase presto orfano di entrambi i genitori. Entrato nel collegio dei Benedettini di Saint Benoît-sur-Loire, fu avviato verso la carriera ecclesiastica, ma nel 1789 in Francia scoppiò la Rivoluzione ed egli cambiò decisamente orientamento, avvicinandosi agli ambienti giacobini. Rischiò di essere ghigliottinato durante il Terrore, ma fu salvato dalla caduta di Robespierre. Appassionatosi di Matematica, rivelò ben presto un intelletto eccezionale e si recò a studiare alla École Normale Supérieure di Parigi, avendo come insegnanti pezzi grossi del calibro di Joseph-Louis Lagrange (1736-1813) e Pierre-Simon de Laplace (1749-1827). Nel 1798 accompagnò Napoleone Bonaparte nella sua spedizione in Egitto insieme a molti altri scienziati; in seguito a questa esperienza scrisse le "Recherches sur les sciences et le gouvernement de l'Égypte", in cui riscoprì l'antica astronomia egiziana. Dopo la partenza di Napoleone, il generale Kleber lo coinvolse in delicate missioni diplomatiche. Tornato in Francia nel 1801, fu nominato dal Bonaparte prefetto dell'Isère, con sede a Grenoble; fu lui a realizzare la strada da Grenoble a Torino attraverso le Alpi. Per i suoi meriti scientifici e amministrativi nel 1808 fu nominato Barone dell'Impero. Fourier era ancora prefetto a Grenoble quando Napoleone abdicò il 6 aprile 1814; con un rapido voltafaccia egli giurò fedeltà al nuovo Re di Francia Luigi XVIII, che gli lasciò la prefettura. A Grenoble incontrò il giovane Jean-François Champollion (1790-1832) che, proprio consultando la sua collezione di geroglifici, avrebbe deciso di decifrarli. Alla morte di Jean-Baptiste Delambre (1749-1822), Fourier divenne segretario dell'Académie des sciences e pubblicò la sua opera più famosa, la "Théorie analytique de la chaleur". I suoi interessi spaziano dall'algebra ai fondamenti della meccanica. I suoi ultimi studi furono dedicati alla teoria delle equazioni algebriche, raccolti nell'opera postuma "Analyse des équations déterminées" (1831). Nel 1827 Fourier fu accolto nell'Académie Française; il grande matematico si spense a Parigi a 62 anni il 16 maggio 1830.

Jean Baptiste Joseph Fourier (Auxerre, 21 marzo 1768 – Parigi, 16 maggio 1830)

Nel 1808 Fourier sottopose all'Institut de France una lunga memoria che presentava la prima trattazione matematica della diffusione del calore. Tale data è considerata l'atto di nascita della Fisica Matematica, una nuova disciplina nella quale il comportamento dei sistemi fisici è dedotto da postulati e passaggi matematici, portando a conclusioni che possono essere verificate sperimentalmente, mentre Galileo e Newton erano partiti dalle « sensate esperienze e necessarie dimostrazioni » per dedurre da esse le leggi fisiche. In tale memoria tra l'altro egli presentò per la prima volta quella che oggi è nota come Equazione di Fourier, che noi deriveremo in questa Appendice. Per risolvere tale equazione, egli propose per primo la sviluppabilità di una funzione sotto forma di una serie di funzioni trigonometriche, oggi conosciuta come Serie di Fourier. Questa sviluppabilità contraddiceva però le opinioni più diffuse sulle funzioni e sulle serie, e in particolare le idee del celebre Lagrange, cosicché il suo lavoro rimase a lungo inedito, ma infine si rivelò uno degli strumenti di calcolo più importanti dell'Analisi Matematica, applicato ad ogni campo della Fisica e dell'Ingegneria. In un'ulteriore memoria sul calore, Fourier introdusse un altro fondamentale strumento di calcolo, la Trasformata di Fourier, fondamentale per la soluzione delle equazioni differenziali.

Per discutere le principali scoperte di Fourier, partiamo da ciò che concerne la propagazione del calore. Essa può avvenire attraverso tre processi: conduzione, convezione ed irraggiamento. In questo paragrafo e nel seguente discuteremo della prima modalità. Essa consiste nella trasmissione del calore senza spostamento di materia e senza alterazione macroscopica del mezzo conduttore. La propagazione del calore per conduzione è caratteristica dei corpi solidi, che si distinguono in buoni conduttori, come i metalli, e in cattivi conduttori, come legno, vetro, lana, eccetera. Tutti infatti sappiamo che non è igienico afferrare a mani nude i manici di metallo di una pentola posta sul fuoco, se non vogliamo ustionarci; molto meglio usare allo scopo delle presine di stoffa o di plastica. A questo scopo, uno strumento di laboratorio usato un tempo per dimostrare la diversa conduzione del calore da parte di diversi materiali è la cosiddetta cassetta di Ingenhousz, dal nome del suo inventore, l'olandese Jan Ingenhousz (1730-1799). Si tratta di una cassetta a forma di parallelepipedo, aperta verso l'alto per potervi versare acqua calda. Sulla faccia anteriore sono applicate delle sbarrette di materiale differente ma della stessa sezione (ferro, rame, zinco, piombo...), tutte ricoperte da uno strato di cera d'api. La quantità di cera fusa e colata da ogni sbarretta dipende dalla conducibilità termica del materiale di cui è composta, il che permette di dimostrare che i vari materiali conducono il calore in maniera differente: la cera intorno alla sbarretta di rame si è già sciolta tutta, mentre ancora è agli inizi lo scioglimento della cera intorno alla sbarretta di piombo.

In realtà la conduzione avviene, in misura minore, anche nei fluidi, ma in essi tale fenomeno è mascherato dalla convezione (vedi § A.3). Il meccanismo di conduzione del calore, studiato approfonditamente da Fourier, è il più semplice, e può essere espresso da relazioni analitiche di grandissima importanza ai fini pratici. Consideriamo allo scopo un solido a forma di parallelepipedo con le due superfici maggiori S distanti L. Se si riscalda una delle due superfici S si registra una differenza di temperatura, diciamo ΔT, tra di esse. Supponendo le superfici minori ben isolate, per il Secondo Principio della Termodinamica il calore si diffonde dentro il corpo solamente verso la superficie opposta a temperatura minore. Sperimentalmente si dimostra che il calore P trasferito per unità di tempo è direttamente proporzionale alla superficie e alla differenza di temperatura ed inversamente proporzionale allo spessore L:

          (A.1)

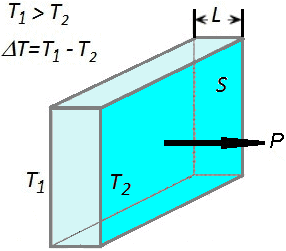
La costante λ è detta costante di conducibilità termica, e la si misura in W / m K. Eccone alcuni valori:

Siccome P è pari al calore Q che trafila diviso l'intervallo di tempo Δt, la (A.1) può essere riscritta:

Esempio A.1: Le due superfici di un muro a facce piane e parallele distanti tra loro L = 40 cm e di dimensioni 4 m x 3 m sono mantenute a temperature costanti T₁ = 34°C e T₂ = 14°C. Sapendo che λ = 0,50 W m^–1 K^–1, trovare la quantità di calore che attraversa il muro in tre minuti.

Dato che S = 12 m², ΔT = 34° – 14° = 20°C e Δt = 180 s, utilizzando la (A.1) scritta in termini di energia si ottiene subito:

Esempio A.2: Nella parete dell'Esempio A.1 viene aperta una finestra di vetro di dimensioni 1 m x 2 m ed è spessa 2 cm. Tutti gli altri dati restano gli stessi. La costante di conducibilità termica del vetro vale circa λ = 1 W m^–1 K^–1. Quanto vale ora il calore che attraversa la parete in tre minuti?

Stavolta la parete non è tutta in laterizi; di essa, 2 m² sono occupati dalla finestra di vetro e 12 – 2 = 10 m² dal muro in mattoni. Il calore che attraversa questi ultimi è ora pari a:

Mentre il calore che attraversa la finestra in vetro è pari a:

Sommando i due risultati si ottiene un calore totale di 45.000 + 360.000 = 405.000 J: un risultato decisamente maggiore della parete in soli mattoni! Le finestre dunque lasciano fuggire parecchio calore, ma ovviamente non è possibile rinunciare ad esse. Per questo, per limitare le perdite, si utilizzano strategie come i doppi vetri.

Esempio A.3: Per effetto di una differenza di temperatura pari a ΔT = 50°C tra le facce piane e parallele di una parete di superficie S = 10 m², in un minuto passa attraverso la parete un calore pari a Q = 50.000 J. Nell'ipotesi che il processo avvenga in regime stazionario e che la costante di conducibilità termica valga λ = 0,75 W m^–1 K^–1, determinare lo spessore della parete.

Stavolta occorre usare la formula inversa, ricordando che Δt = 1 min = 60 s:

.

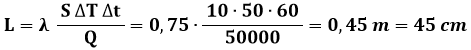
A.2  L'equazione di Fourier

Utilizziamo la precedente espressione per scrivere l'equazione della propagazione del calore. Come etto sopra, sarà indispensabile sfruttare gli strumenti dell'Analisi Matematica; chi non li conosce, trascuri questo paragrafo per passare al successivo. In termini infinitesimi, la precedente può essere riscritta:

          (A.2)

dove ∂T/∂n è la derivata parziale della temperatura misurata in direzione perpendicolare alla superficie S (finora in questo ipertesto non avevamo ancora mai usato le derivate parziali). Facciamo ora le seguenti ipotesi:

• il sistema è omogeneo ed isotropo, cioè il materiale di cui è costituito è uguale in ogni punto e in ogni direzione;

• escludiamo le trasformazioni di calore in lavoro e viceversa.

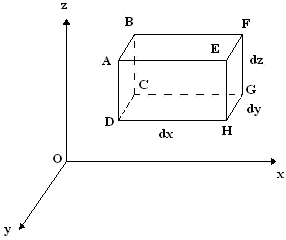
Preso un generico elemento di volume dV = dx dy dz interno al sistema, nel tempo dt, attraverso le sei facce che delimitano dV, si trasmette una quantità di calore d*Q₁, pari alla somma algebrica delle quantità di calore trasmesse attraverso le singole facce, ma anche una quantità di calore d*Q₂, sviluppata all'interno di dV attraverso un fenomeno termodinamico qualsiasi. Supponiamo che nel tempo dt la temperatura di dV subisca una variazione dT. Imponendo che non si verifichino trasformazioni con cambiamento di stato e reazioni chimiche, e trascurando anche le variazioni di volume si può applicare la conservazione dell'energia:

d*Q₁ + d*Q₂ = d*Q

Usando per d*Q l'equazione del calorimetro (1.1), se il calore ha come unico effetto quello di variare la temperatura, detto c il calore specifico, si ha:

d*Q = c dm dT

dove dm è la massa dell'elemento infinitesimo del nostro sistema termodinamico. Introducendo la densità ρ, il volume infinitesimo dV e l'intervallo di tempo infinitesimo dt, la precedente di può riscrivere:

Sostituendo si ottiene:

          (A.3)

Utilizziamo adesso la (A.2) per esprimere le quantità di calore trasmesse rispettivamente attraverso le facce ABCD (ascissa x) e EFGH (ascissa x + d x):

Quest'ultima relazione può essere sviluppata in serie di Taylor arrestata al primo ordine, assumendo che λ sia costante rispetto ad x, per le ipotesi di isotropia e omogeneità fatte, e considerando anche una dipendenza trascurabile dalla temperatura):

Le quantità di calore che si trasmettono nel verso delle x crescenti sono considerate positive. Nella coppia di facce ortogonali all'asse x si avrà una quantità di calore residua nel materiale pari a:

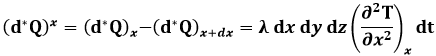
dove (d*Q)_x rappresenta la quantità di calore entrante nell'elemento di materia, mentre (d*Q)_x+dx rappresenta la quantità di calore uscente da esso.

Ora, dx dy dz è l'elemento di volume dV, per cui la precedente si può riscrivere così:

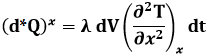
Ripetendo il procedimento per le altre due coppie di facce ortogonali alle direzioni y e z, si ottiene l'espressione della quantità di calore dQ₁:

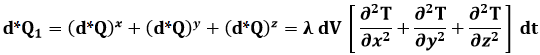
Questa formula può essere riscritta in maniera compatta usando il cosiddetto operatore nabla:

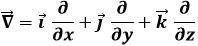
Tale operatore è stato introdotto dal matematico irlandese Sir William Rowan Hamilton (1805-1865), e prende nome da uno strumento musicale a corda della tradizione ebraica europea, il nebel, una cetra con una cassa acustica di forma triangolare (e Sir Hamilton conosceva benissimo la lingua e le tradizioni ebraiche). Dall'operatore nabla deriva il cosiddetto rotore o operatore laplaciano, che prende il nome dal famoso Pierre Simon de Laplace (1749-1827):

Detta q_V la quantità di calore sviluppata nell'unità di tempo nell'unità di volume del sistema, inoltre, possiamo scrivere:

Sostituendo i risultati ottenuti nella (A.3), si ottiene:

Semplifichiamo ambi i membri per dV dt, dividiamo i due membri della precedente per λ e introduciamo una nuova grandezza, la diffusività termica, misurata in m² / s:

Otteniamo così finalmente l'equazione di Fourier:

          (A.4)

che si può riscrivere in forma compatta:

Essa è la prima equazione differenziale alle derivate parziali della storia della Fisica Matematica. Un importante caso particolare è quello in cui non si ha alcuna sorgente interna di calore. Allora q_V = 0 e la (A.4) diventa:

          (A.5)

In questo caso, lo stesso Fourier sviluppò per primo un metodo analitico per la risoluzione di tale equazione. Esso consiste nel supporre che la funzione risolutiva possa essere espressa come prodotto di altre due funzioni, di cui una dipendente solo dalle coordinate spaziali e l'altra solo dal tempo, così:

Sotto questa ipotesi, la (A.5) diventa:

cioè:

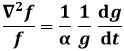
E quindi, dato che il primo membro può dipendere solo dalle coordinate spaziali, mentre il secondo può dipendere solo dal tempo, entrambi i termini devono risultare per forza costanti:

Siamo così arrivati a due equazioni differenziali relativamente più semplici da risolvere. Trovate le soluzioni di tali equazioni, se il loro prodotto soddisfa le condizioni iniziali del problema, ciò significa che effettivamente il sistema termodinamico in esame può essere descritto da una soluzione del tipo proposto, che rappresenta la temperatura sotto forma del prodotto di due funzioni, l'una dipendente solo dalle coordinate spaziali, l'altra dipendente solo dal tempo. In caso contrario, bisognerà cercare soluzioni di tipo diverso, come vedremo nell'esempio D) qui sotto.

Se invece il regime è stazionario, allora ∂T / ∂t = 0 (la derivata di una costante è nulla) e la (A.4) diventa:

In assenza di sorgenti interne di calore e in regime stazionario, si verificano entrambe le condizioni sopra prospettate e l'equazione si semplifica parecchio:

          (A.6)

che si può riscrivere:

Questa è la famosa equazione di Laplace. Essa ha moltissime applicazioni in Fisica Matematica: se l'incognita è una concentrazione, essa esprime la legge della diffusione o legge di Fick; se l'incognita è un potenziale elettrostatico, essa descrive il campo elettrico in ogni punto nel caso in cui non siano presenti sorgenti del campo. Nel nostro caso l'incognita è il campo di temperature T = T ( x ; y ; z ; t ), e la soluzione generale risolve il problema della conduzione del calore nei corpi solidi.

In coordinate cilindriche ( r ; φ ; z ), utili quando si ha a che fare con cilindri cavi percorsi da fluidi caldi (cioè con tubazioni), la (A.4) assume una forma più complicata:

          (A.7)

Fissati la porzione di spazio V in cui si vuole determinare la distribuzione di temperatura e la superficie S che la delimita, per risolvere l'equazione occorre conoscere la distribuzione di temperatura all'istante iniziale, cioè all'istante nel quale si inizia a considerare il fenomeno, e ciò che accade sulla superficie del sistema in ogni istante successivo. Si parla in tal caso di condizione iniziale e di condizioni al contorno. Bisogna notare che, perchè si abbia una certa simmetria nella distribuzione di temperatura, non basta che essa si rispecchi nella simmetria del sistema in esame, ma occorre che abbiano tale simmetria anche le condizioni iniziali e le condizioni al contorno. Si risolvono in maniera semplice quei problemi in cui la temperatura risulta funzione solo di una coordinata spaziale e del tempo. Vediamone alcuni esempi.

A) Si consideri una parete piana infinita lungo le direzioni y e z (cioè molto più estesa nelle direzioni y e z rispetto allo spessore lungo la direzione x); sia s lo spessore in direzione x. Sulle due superfici che la delimitano vi sono due temperature prefissate T₁ e T₂, costanti ed uniformi su di esse. Poniamo inoltre che dentro la parete non vi sia alcuna sorgente di calore (q_V = 0). La (A.5) diventa allora:

Se poi siamo in regime stazionario, ∂T / ∂t = 0 e la precedente si riduce semplicemente a:

Essa va integrata con le seguenti condizioni al contorno: per x = 0, T = T₁; per x = s, T = T₂. L'integrale generale della precedente è:

E imponendo le suddette condizioni al contorno si otterrà:

          (A.8)

La temperatura dunque varia linearmente lungo l'asse x da T₁ a T₂:

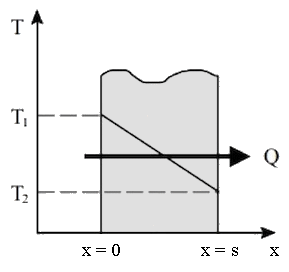
Supponiamo invece che dentro il muro sia presente una sorgente di calore in regime stazionario. La (A.4) diventa:

In questo caso la soluzione generale è del tipo:

Sostituendo nella precedente ed imponendo le condizioni al contorno, si trova la soluzione cercata:

Si noti che, se q_V = 0, si ritrova la (A.8). Come si vede, la temperatura in un punto qualsiasi si ottiene sommando alla temperatura di una delle due pareti un contributo lineare funzione della posizione, dipendente dalle condizioni al contorno e dalla generazione di calore, oltre a un ulteriore contributo, con andamento parabolico, dovuto alla sola generazione di calore.

B) si consideri un cilindro cavo, infinito in direzione assiale e di raggi interno ed esterno R_i ed R_e, con temperature T₁ e T₂ costanti ed uniformi sulle superfici che lo delimitano. Non vi è generazione di calore al suo interno.

Con queste condizioni, la temperatura T risulta funzione solo della coordinata radiale r. L'equazione di Fourier (A.7) allora si riduce alla forma:

che si può riscrivere:

Essa va integrata con le seguenti condizioni al contorno: per r = R_i, T = T₁; per r = R_e, T = T₂. L'integrale generale della precedente è:

          (A.9)

Osserviamo ora che, essendo:

risulta:

Ora, se:

cioè se R_e – R_i << R_i (lo spessore del tubo è piccolo rispetto al raggio interno), si può sviluppare la precedente in serie di Taylor ed arrestare lo sviluppo al primo termine, ottenendo:

E analogamente se r – R_i << R_i si avrà:

Allora la (A.9) diventa:

Notiamo che, in questa approssimazione, il profilo di temperatura attraverso il tubo si può approssimare con quello di una lastra piana di spessore s = R_e – R_i, se come variabile x usiamo x = r – R_i: la formula appena ricavata si riconduce infatti alla (A.8).

C) si consideri ora una barra cilindrica piena, infinita in direzione assiale e di raggio esterno R. Tale barra abbia una temperatura assegnata T₀ costante ed uniforme sulla sua superficie esterna, mentre in essa vi sia una sorgente di calore per unità di volume costante e pari a q_V.

In queste condizioni, la temperatura risulta funzione solo della coordinata radiale r, e l'equazione di Fourier (A.7) si riduce a:

E le condizioni al contorno? Anzitutto, per r = R, T = T₀; ma ne occorre un'altra, trattandosi di un'equazione differenziale del secondo ordine.  Per questo, notiamo che per  la potenza generata in una barra di raggio r tende a zero con r², mentre la superficie da cui tale potenza deve uscire tende a zero solo con r, quindi per compensare questo fatto dovrà tendere a zero anche la derivata di T rispetto ad r: dT / dr = 0 per r = 0. Risulta allora:

La dipendenza di T da r è rappresentata dunque da una parabola con vertice in r = 0. Il suo massimo vale:

D) Consideriamo infine una parete solida di profondità infinita, la cui temperatura è portata a T = T₀ e mantenuta tale indefinitamente. Ipotizziamo che non vi sia alcuna generazione di calore al suo interno.

Considerando l'asse x perpendicolare alla parete e ponendo x = 0 sulla parete stessa, l'equazione si semplifica così:

Le tre condizioni al contorno sono le seguenti:

T = 0 per t = 0 e x qualunque
T = T₀ per x = 0 e t > 0
T = 0 per x → ∞ e t > 0

Si può dimostrare che un integrale generale della equazione in esame è il seguente:

nella quale il termine:

è una nuova variabile adimensionale, funzione delle due variabili tradizionali x e t. Per questa nuova variabile adimensionale, le condizioni al contorno diventano:

T = 0 per t = 0 e x qualunque ( η → ∞ )
T = T₀ per x = 0 e t > 0 ( η = 0 )
T = 0 per x → ∞ e t > 0 ( η → ∞ )

Quindi si riconducono a due sole, perchè la prima e la terza coincidono. La funzione:

viene chiamata "funzione degli errori di Gauss", perchè riveste una grande importanza in statistica, nello studio della distribuzione degli errori casuali. Essa è indicata con la simbologia erf η (dall'inglese "error function") e può venire rappresentata in questo modo:

Imponendo le condizioni al contorno suddette si trovano facilmente i valori delle costanti, che valgono c₁ = – T₀ e c₂ = T₀. Di conseguenza la temperatura nella parete solida ha la seguente distribuzione:

T = T₀ ( 1 – erf η )

Tale funzione è facilmente rappresentabile, come mostra il diagramma seguente:

Si può notare che, per η = 1 / 2, anche T vale circa T₀ / 2. D'altra parte, η = 1 / 2 corrisponde ad una coppia di valori ( x ; t ) tali per cui al valore considerato di x esiste un valore di t per cui η = 1 / 2, e quindi anche T = T₀ / 2. In altre parole, in corrispondenza di ogni posizione esiste un tempo dopo il quale la temperatura raggiunge una temperatura rispetto al valore iniziale pari alla metà della temperatura imposta sulla parete (dove x = 0). Si può osservare che η = 1 / 2 corrisponde a:

x² = α t

A pari t, x risulta proporzionale alla radice quadrata di α, quindi il calore penetra nel materiale tanto più quanto più è elevato la diffusività termica del materiale, come mostra il seguente grafico:

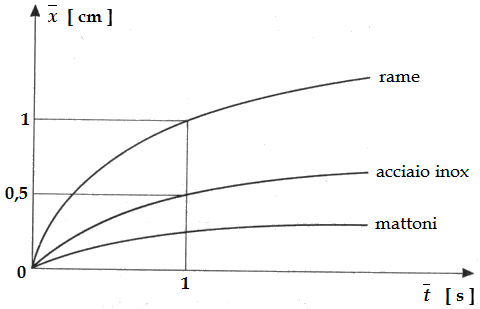
Ad esempio per il rame, per il quale α = 1 cm² / s, per t = 1 s risulta  con x = 1 cm, mentre per l'acciaio inox, per il quale la diffusività termica α ha un valore pari a circa un quinto di quello del rame, la penetrazione del calore dopo un secondo è di circa 0,5 cm.

Poiché la funzione erf η tende assai rapidamente al suo asintoto, (come si vede dal grafico soprastante, già per η = 2 è erf η > 0,99), e quindi la soluzione trovata in questo caso è accettabile anche per una parete di spessore finito. I valori assoluti di x e di t per cui vale questa approssimazione dipendono ovviamente anche da α, ovvero dalla natura del materiale.

.

A.3  La convezione del calore

Il secondo meccanismo di propagazione del calore consiste nella convezione (dal latino "cum" e "veho", cioè "trasporto"), cioè la trasmissione del calore accompagnata da trasporto di materia. Questo fenomeno naturalmente è possibile solo nei fluidi, ed avviene per mezzo dei cosiddetti moti convettivi. Poniamo infatti una pentola trasparente piena d'acqua sopra il fuoco. La prima a scaldarsi è l'acqua a contatto con il fondo, che si dilata, aumentando di volume. Siccome la densità è data dal rapporto tra massa e volume, la densità dell'acqua diminuisce e di conseguenza, per il Principio di Archimede, sale verso l'alto. Così facendo, spinge verso il basso l'acqua più fredda, che a sua volta di riscalda, viene a galla, e così si forma una circolazione di fluido, che dura finché dura l'apporto di calore. Gettando la pasta nell'acqua che bolle, si evidenziano chiaramente questi moti convettivi attraverso il moto dei maccheroni.

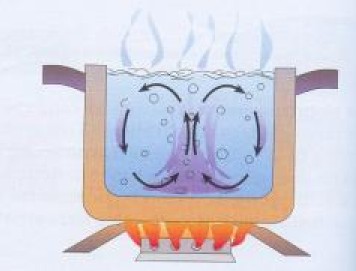
Sono i moti convettivi dell'aria di una stanza, innescati da un termosifone acceso, a permettere il riscaldamento omogeneo di una stanza della nostra casa in inverno:

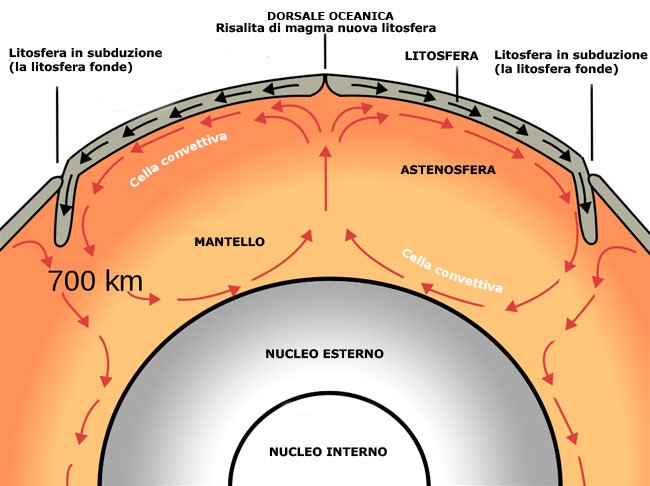
Inoltre, i moti convettivi all'interno della Terra spiegano la dinamica geologica del nostro pianeta e, in particolare, la deriva dei continenti. Infatti il mantello terrestre si trova allo stato semifluido; di conseguenza, essendo il nucleo molto più caldo della crosta terrestre, dal fondo fino alla sommità di esso si formano delle celle convettive: il magma risale dalle profondità della Terra fin sotto la crosta, nella cosiddetta astenosfera, poi scorre sotto di essa e trasporta la crosta continentale come su un tapis-roulant. Il magma che fuoriesce in superficie forma una dorsale oceanica, una serie di vulcani sottomarini che eruttano e producono nuova crosta basaltica, cioè oceanica, mentre i continenti si allontanano e fra di essi si apre un oceano. Questo è il processo con il quale, nel corso degli ultimi 150 milioni di anni, si è aperto l'Oceano Atlantico. In certi punti la vecchia crosta continentale scivola sotto altra crosta, rifondendo: è il cosiddetto fenomeno della subduzione, con il quale al contrario gli oceani si chiudono! Per maggiori informazioni, cliccate qui.

Anche all'interno del Sole si formano celle convettive: esso infatti è una massa di plasma, il cui nucleo si trova a 15 milioni di gradi, e la cui superficie raggiunge i 5777 K. Attraverso enormi celle convettive il calore viene trasportato dalle zone più calde nel nucleo a quelle più fredde ridistribuendo la temperatura. Nel Sole attorno al nucleo, dove avvengono le reazioni di fusione, c'è uno strato di gas detto strato radiativo, a sua volta circondato da uno strato chiamato zona convettiva, con uno spessore di 150.000 km. Dalla zona radiativa l'energia viene trasportata attraverso i fotoni, che vengono trasferiti da uno ione ad un altro in un processo molto lento, di qualche milione di anni, e si muove verso l'esterno dove la temperatura del gas diminuisce; gli elettroni si ricombinano e possono così riassorbire un fotone e possono essere strappati di nuovo all'atomo: tutto ciò provoca un rallentamento della radiazione. Così si sviluppano moti convettivi che si innalzano verso la superficie, dove si raffreddano e provocando il trasferimento dell'energia, che altrimenti resterebbe all'interno.

Celle convettive esistono anche nell'atmosfera terrestre. Ne è un esempio la cosiddetta Cella di Hadley:, che prende nome dal meteorologo dilettante britannico George Hadley (1685-1768): l'aria si innalza all'equatore in conseguenza del forte riscaldamento e raggiunge i limiti superiori della troposfera, che alle latitudini equatoriali raggiunge e supera i 12 km di quota. Una volta raffreddata, l'aria ridiscende in corrispondenza delle latitudini subtropicali, causando aree anticicloniche permanenti, come ad esempio il famoso Anticiclone delle Azzorre, oltre a quell'insieme di fenomeni che danno vita alle zone più secche e desertiche del nostro pianeta. L'aria ridiscesa finisce per convergere nuovamente al suolo verso l'equatore attraverso i venti alisei, che spirano da nord-est verso sud-ovest nell'emisfero boreale e da sud-est-verso nord ovest in quello australe:

Veniamo ora ad una trattazione sintetica del fenomeno della convezione. Indichiamo con Ts la temperatura della parete e con Tf la temperatura del fluido molto lontano dalla parete calda con la quale esso scambia calore per convezione. Si può verificare sperimentalmente che il calore Q scambiato per unità di tempo tra la parete e il fluido è direttamente proporzionale alla superficie S della parete e alla differenza delle due temperature. Il coefficiente di proporzionale è chiamato coefficiente di convezione termica, lo si indica con h e lo si misura in W m^–2 K^–1:

          (A.10)

Ecco alcuni ordini di grandezza del coefficiente h:

Esempio A.4: Un termosifone misura 1,25 x 0,8 m. Esso si trova alla temperatura di 50°C mentre la stanza in cui è montato ha una temperatura di 20°C. Qual è il calore che il calorifero trasmette alla stanza in dieci minuti, assumendo h = 25 W m^–2 K^–1?

Il termosifone ha una superficie S = 1 m², e la differenza di temperatura è pari a 50° – 20° = 30°C. Usando la (A.10) si ha:

Q = h S (Ts – Tf) Δt = 25 x 1 x 30 x 600 = 450.000 J

Ma cosa vuol dire "aria in convezione naturale" ed "aria in convezione forzata", come riportato nella tabella soprastante? Il fatto è che la trasmissione del calore per convezione può avvenire in due diverse modalità: per convezione naturale e per convezione forzata. Si ha convezione naturale quando il moto del fluido avviene unicamente a causa del trasferimento di calore in atto, giacché il fluido caldo si dilata, la sua densità diminuisce e si innescano spontaneamente dei moti convettivi. Si ha invece convezione forzata quando il fluido che lambisce la parete è forzato a muoversi mediante un'azione esterna di pompaggio. Nel caso della convezione forzata, il coefficiente di convezione h dipende dai seguenti parametri:

• dalle caratteristiche fisiche del fluido, e in particolare dalla densità ρ, dalla viscosità μ, dal calore specifico a pressione costante c_P e dalla conducibilità termica k.

• dallo stato di moto del fluido, cioè dalla sua velocità media v;

• dalla geometria della parete, individuata tramite un parametro geometrico D, che per i condotti rappresenta il diametro, e per le pareti lambite da un fluido rappresenta una certa distanza dalla parete.

Ne risulta che h deve essere funzione dei sei parametri sopra elencati:

h = f ( ρ ; μ ; c_P ; k ; v ; D )

Supponiamo che tale funzione f sia rappresentata dal prodotto di una costante per ciascuno dei sei parametri elevati ad un certo esponente da determinare:

h = cost. x ρ^a μ^b c_P^c k^d v^e D^f          (A.11)

Naturalmente le dimensioni fisiche del primo membro devono essere uguali a quelle del secondo membro; possiamo perciò scrivere un'equazione dimensionale.

h si misura in W m^–2 K^–1, cioè in Kg s^–3 K^–1
ρ si misura in m^–3 Kg
μ si misura in Pa s, cioè in m^–1 Kg s^–1
c_P si misura in J Kg^–1 K^–1, cioè in m² s^–2 K^–1
k si misura in W m^–1 K^–1, cioè in m Kg s^–3 K^–1
v si misura in m s^–1
D si misura in m

Di conseguenza la (A.11) diventa:

Kg s^–3 K^–1 = m^–3a Kg^a m^–b Kg^b s^–b m^2c s^–2c K^–c m^d Kg^d s^–3d K^–d m^e s^–e m^f

che si può riscrivere:

Kg s^–3 K^–1 = m^{– 3a – b + 2c + d + e + f} Kg^{a + b +d} s^{– b – 2c – 3d – e} K^{– c – d}

Essa fornisce il sistema:

– 3a – b + 2c + d + e + f = 0
   a + b +d = 1
– b – 2c – 3d – e = – 3
– c – d = – 1

Si tratta di quattro equazioni in sei incognite, dunque quattro di tali incognite risulteranno funzione delle altre due. Risolvendo il sistema si ha:

a = e
b = c – e
d = 1 – c
f = e – 1

Allora la (A.11) si può riscrivere:

h = cost. x ρ^e μ^{c – e} c_P^c k^{1 – c} v^e D^{e – 1}

Raggruppiamo i termini con lo stesso esponente:

Ecco un altro modo di riscriverla:

          (A.12)

Quelli che abbiamo trovato sono tre gruppi di numeri adimensionali, che in Termodinamica hanno una grandissima importanza. Il primo:

è detto numero di Nusselt, dal nome dell'ingegnere tedesco Kraft Ernst Wilhelm Nusselt (1882-1957). Dato che il numeratore è legato al coefficiente di convezione termica e il denominatore al coefficiente di convezione, si deduce che il numero adimensionale di Nusselt esprime il rapporto tra il flusso di calore scambiato per convezione e quello scambiato per conduzione. Il secondo:

è chiamato numero di Prandtl, in onore dell'ingegnere e fisico tedesco Ludwig Prandtl (1875-1953). Si osservi che esso può essere così riscritto:

Esso dunque rappresenta il rapporto tra il coefficiente di diffusione della quantità di moto μ / ρ e quello del calore k / ρ c_P. Ecco alcuni valori assunti dal numero di Prandtl per diversi fluidi:

Infine, il terzo numero adimensionale:

è chiamato numero di Reynolds, e prende il nome dal fisico e ingegnere nordirlandese Osborne Reynolds (1842-1912) che lo introdusse nel 1883 eseguendo esperimenti sul flusso all'interno di tubi a sezione circolare trasparente ad asse rettilineo nel quale circolava un flusso a portata costante, nel quale, per mezzo di un ago, veniva iniettato un colorante in modo da evidenziare il tipo di flusso. Esso rappresenta il rapporto fra le forze d'inerzia e quelle viscose all'interno di un fluido. Tali forze infatti possono essere riscritte così:

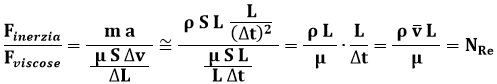
Esso rappresenta quindi il discriminante tra due diversi tipi di moto. Per bassi valori del numero di Reynolds, siamo nel cosiddetto regime laminare: le particelle del fluido si muovono parallelamente alle pareti del condotto, senza interagire le une con le altre mediante forze perpendicolari al loro moto. Invece, per alti valori del numero di Reynolds, siamo nel cosiddetto regime turbolento: le particelle del fluido hanno velocità distribuite in tutte le direzioni possibili, non solo parallele alle pareti del condotto, e di conseguenza formano dei vortici. Tutti noi abbiamo avuto occasione di osservare questi due tipi di moto del fluido: se apriamo appena appena un rubinetto, esce solo un sottile filo d'acqua, nel quale tutte le molecole cadono verso il basso, ma se lo apriamo maggiormente, il fluido comincia a dare vita a vortici e turbolenze. Sperimentalmente si verifica che per valori del N_Re minori di 2500, il moto del fluido è di tipo laminare, mentre per valori maggiori diventa turbolento. Non si tratta però di un valore valido in assoluto, perchè le turbolenze del fluido possono essere innescate anche da altri parametri non compresi nella definizione del numero di Reynolds. Quest'ultimo comunque viene universalmente considerato un indice di turbolenza del moto.

La (A.12) in definitiva può essere così riscritta:

          (A.13)

dove la costante moltiplicativa e gli esponenti c ed e vanno determinati sperimentalmente. Nei gas le cui caratteristiche si avvicinano a quelle del gas perfetto, il numero di Prandtl varia poco al variare dello stato del gas, ed anzi è circa uguale per i gas le cui molecole sono formate dallo stesso numero di molecole: approssimativamente N_Pr = 0,67 per gas monoatomici, N_Pr = 0,70 per gas biatomici e N_Pr = 0,89 per gas triatomici. La (A.13) allora si può semplificare così:

Consideriamo il caso di fluidi poco viscosi e a bassa conducibilità termica (più bassa, per capirci, di quella dei metalli liquidi), ed assumiamo che D sia il diametro del condotto nel quale il fluido scorre, come avviene nella maggior parte degli scambiatori di calore reali. Le esperienze condotte usando tali fluidi hanno permesso di arrivare a scrivere alcune formule empiriche, di cui quella più utilizzata è la cosiddetta Formula di Dittus-Boelter. Essa prende il nome dagli ingegneri americani Frederick William Dittus (1897-1987) e Llewellyn Michael Kraus Boelter (1898-1966) che la misero a punto nel 1930; è valida per salti di temperatura tra parete e fluidi non troppo elevati e per  questi intervalli di valori dei parametri adimensionali in gioco:

L / D > 60
0,7 < N_Pr < 120
10.000 < N_Re < 120.000

Tale formula può essere scritta in questi termini:

In essa n vale 0,4 se il fluido viene riscaldato, 0,3 se viene raffreddato. Nonostante la sua semplicità è notevole la varietà di fluidi e di condizioni per la quale essa può essere ritenuta valida: essa dà risultati soddisfacenti per l'acqua fino a pressioni e temperature elevate (140 atmosfere e 300°C) e per numeri di Reynolds fino a 10⁶! Ecco tabulata la dipendenza di N_Nu da N_Re in scala logaritmica, confrontata con i risultati sperimentali usando una miscela di acqua e di glicole etilenico (C₂H₆O₂) a 70°C (è tratta da questo sito):

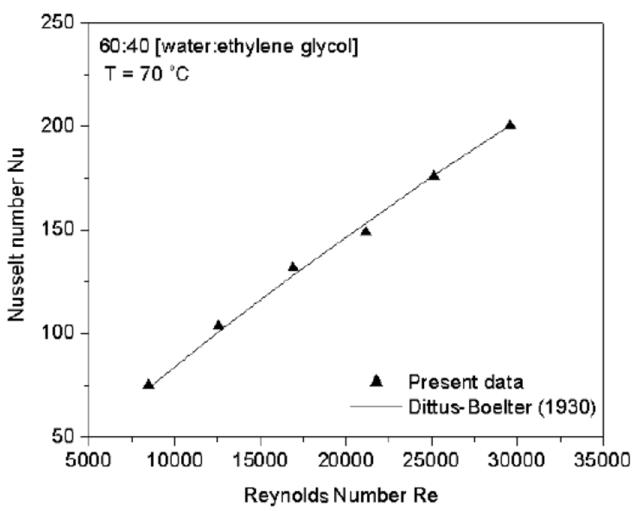
Le relazioni empiriche del tipo della (A.13), come detto, valgono in caso di convezione forzata. E nel caso di convezione naturale? È possibile ripetere calcoli analoghi? Sì, ma stavolta essi sono molto più complicati. Infatti in questo caso h dipenderà, oltre che dalle caratteristiche fisiche del fluido ρ, μ, c_P e k, anche dal coefficiente di dilatazione isobara α, responsabile della variazione di densità che innesca i moti convettivi, che si misura in K^–1. Inoltre lo stato di moto del fluido non è rappresentabile in questo caso come un parametro indipendente, ma viene descritto dalla forza agente sull'unità di volume del fluido, espressa dalla formula ρ g α ( T_s – T_f ), dove ρ è la densità media del fluido, g l'accelerazione di gravità, T_f la temperatura del fluido e T_s quella della parete. Infine, la geometria della superficie della parete è individuata oltre che da un parametro geometrico D anche dall'orientamento di tale superficie di scambio rispetto al campo gravitazionale terrestre. Utilizzando l'analisi dimensionale già sfruttata nel caso di convezione forzata, è possibile scrivere l'equivalente della (A.13), che appare in questa forma:

          (A.14)

In essa, il numero di Reynolds è sostituito da un nuovo numero adimensionale, detto numero di Grashof dal nome dell'ingegnere tedesco Franz Grashof (1826-1893):

Esso esprime il rapporto delle forze di galleggiamento e delle forze viscose di un fluido:

Dunque esso viene considerato un indice della facilità del fluido a muoversi nella geometria considerata per effetto di differenze di temperatura, cioè un indice della facilità al moto convettivo naturale. Questo numero inoltre può essere ricondotto ad una generalizzazione del numero di Reynolds. Infatti nell'espressione:

v è di solito una velocità impressa dall'esterno, essendo stato introdotto per la convezione forzata. Invece nella convezione naturale v è determinata dallo stato termico del fluido e dalle caratteristiche del condotto, e sarà tanto più elevata quanto maggiore è la sezione D² del condotto medesimo, quanto maggiore è il campo di forze ρ g α ( T_s – T_f ) in cui il fluido è immerso, e tanto minore quanto maggiore è l viscosità μ. In altre parole, si può scrivere:

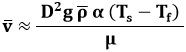
Sostituendo quest'ultima espressione nella definizione del numero di Reynolds, si trova proprio il numero di Grashof, che è il suo equivalente per la convezione naturale.

John William Strutt, Lord Rayleigh (1842-1919)

Anche la (A.14), come la (A.13), può essere ricondotta a una funzione di un solo numero adimensionale, non solo quando il numero di Prandtl è costante (come nel caso dei gas perfetti), ma anche quando le accelerazione nel fluido sono trascurabili: un caso molto comune nella convezione naturale, perchè i moti convettivi in generale sono lenti. In tal caso scompaiono dalle equazioni di bilancio alcuni termini in ρ, e  risulta funzione del prodotto dei numeri di Grashof e di Prandtl:

Il prodotto di questi due numeri è una nuova realtà adimensionale chiamata numero di Rayleigh, che prende il nome dal britannico John William Strutt, 3º barone di Rayleigh (1842-1919). Premio Nobel per la Fisica nel 1904:

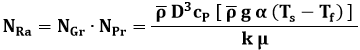
Il numero di Rayleigh può essere interpretato come il rapporto tra forze di galleggiamento e forze d'attrito viscoso, e quindi è considerato un indice del contributo dei moti naturali allo scambio termico convettivo.

Esistono per la convezione naturale relazioni empiriche analoghe alla Formula di Dittus-Boelter? Naturalmente sì. Per fluidi poco viscosi con pareti verticali piane o cilindriche di grande diametro (in questo caso la dimensione caratteristica D è l'altezza della parete), e per 10³ < N_Ra < 10⁸, si può scrivere:

In questa formula, le proprietà fisiche sono valutate alla temperatura media ( T_s + T_f ) / 2.

Per la valutazione delle dispersioni di calore in aria a pressione atmosferica e a temperatura poco diversa dall'ambiente, esistono alcune relazioni molto semplificate, dedotte dalla precedente, in cui intervengono solo il salto termico ΔT misurato in °C e una dimensione geometrica caratteristica del corpo. Se il coefficiente di convezione h è espresso in W m^–2 °C^–1, per pareti verticali, piastre e cilindri di altezza L misurata in metri:

    per 10⁴ < N_Ra < 10⁹

e per cilindri orizzontali di diametro D misurato in metri:

    per 10³ < N_Ra < 10⁹

Il valore del numero di Rayleigh che corrisponde al sopraggiungere delle condizioni di convezione è detto numero di Rayleigh critico. Il numero di Rayleigh viene spesso adoperato in geofisica poiché permette di determinare le condizioni di innesco dei moti verticali in fluidi viscosi incomprimibili, la cui temperatura cresce con la profondità, proprio come avviene nel mantello terrestre.

Bisogna aggiungere che esiste un altro numero adimensionale di grande importanza, il cosiddetto numero di Richardson, intitolato al fisico inglese Lewis Fry Richardson (1881-1953). Esso è pari al rapporto tra il numero di Grashof e il quadrato del numero di Reynolds; esprime il rapporto tra l'energia potenziale e l'energia cinetica di un fluido, ma anche il rapporto tra la forza di gravità e la forza inerziale, e quindi misura l'importanza dell'effetto gravitazionale sul moto dei fluidi:

Il numero di Richardson viene utilizzato in aerotecnica per misurare le turbolenze durante i viaggi in aereo. Ma soprattutto esso rappresenta un importante criterio per distinguere tra convezione naturale e forzata:

se N_Ri >> 1 la convezione è naturale;
se N_Ri << 1 si ha convezione forzata.

Se invece N_Ri ≈ 1, si parla di convezione mista: come suggerisce il nome, in questo caso responsabili del moto del fluido sono sia differenze di densità dovute a differenze di temperatura che cause esterne. Essa avviene ad esempio quando si fa uso dei ventilconvettori (termosifoni con ventola); se la ventola è in funzione, l'apporto di calore all'ambiente è dovuto sia alla ventola che al termosifone stesso.

Esempio di ventilconvettore (da questo sito)

A partire dagli anni settanta si è registrato un notevole interesse verso l'uso dei metalli liquidi a basso punto di fusione come fluidi termovettori negli scambiatori di calore. Essi infatti presentano il vantaggio di rimanere allo stato liquido in un intervallo di temperature molto ampio, anche a pressioni relativamente basse. I metalli liquidi di uso più frequente sono il sodio, il potassio, il litio e le loro leghe. Il sodio in particolare era utilizzato per raffreddare i reattori nucleari veloci come il Superphénix di Creys-Malville (Francia). Per saperne di più, cliccate qui.

I metalli liquidi differiscono considerevolmente dagli altri fluidi per la loro elevata conducibilità termica: infatti hanno numeri di Prandtl compresi tra 0,005 e 0,03. Mentre in altri fluidi in moto turbolento la trasmissione di calore è dovuta essenzialmente al forte rimescolamento del fluido, e questa azione è più efficace della trasmissione per conduzione, tanto che il salto termico tra parete e fluido si localizza quasi interamente nello strato fluido vicino alla parete, per i metalli liquidi i due effetti di pura conduzione e di mescolamento sono dello stesso ordine di grandezza. Di conseguenza il salto termico tra parete e fluido si distribuisce in tutto il suo volume. Un criterio per valutare l'efficacia del mescolamento in confronto alla conduzione attraverso il fluido è offerto dal cosiddetto numero di Péclet, così chiamato in onore del fisico francese Jean Claude Eugène Péclet (1793-1857). Esso è pari al prodotto tra i numeri di Reynolds e di Prandtl:

Il numero di Reynolds è un indice della turbolenza del moto, quello di Prandtl è il rapporto tra i coefficienti di diffusione della quantità di moto e del calore. Di conseguenza esso è pari al rapporto tra il prodotto v D che è indice della diffusione turbolenta e il coefficiente di diffusione molecolare del calore, e perciò esso è indice del contributo turbolento allo scambio convettivo di calore:

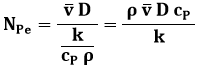
Per N_Pe < 100, in condizioni di moto turbolento la conduzione termica del fluido governa la trasmissione del calore all'interno della zona di turbolenza. Per N_Pe intorno a 1000, invece, la conduzione e il rimescolamento sono ugualmente importanti. Solo per N_Pe > 50.000 il rimescolamento diventa il fenomeno prevalente, e la trasmissione del calore è governata dalla resistenza termica dello strato fluido in prossimità della parete.

Ciò ha un'importante conseguenza. Per i metalli liquidi che fluiscono in un condotto, anche se in moto turbolento, non è più valida la generalizzazione che può essere eseguita per molti altri fluidi, considerando il diametro del condotto come parametro lineare D caratteristico della convezione, se il profilo delle temperature dentro il condotto non è determinato dalla turbolenza del moto, cioè per N_Pe < 50.000. Infatti ciò presupporrebbe una distribuzione della velocità con grandi variazioni nei pressi della parete e con variazioni molto piccole al centro del fluido. Per i metalli liquidi, dunque, occorre trattare separatamente le diverse geometrie dei condotti, e ciò complica notevolmente i calcoli.

Nel caso di condotti a sezione circolare con lunghezza molto maggiore del loro diametro, si può utilizzare la cosiddetta Relazione di Skupinski, ricavata nel 1965 per via teorica supponendo che la diffusività turbolenta della quantità di moto e quella del calore siano pressoché uguali e che il flusso attraverso la parete sia costante:

Invece, supponendo costante la temperatura sulla parete del condotto, è stata ricavata la Relazione di Seban-Shimazaki (1949):

Si osservi che, in relazione agli alti coefficienti di scambio termico ottenibili con i metalli liquidi anche a basse velocità, assume particolare importanza la trasmissione di calore per circolazione naturale in un circuito chiuso. Ciò vale in particolare per gli impianti nucleari veloci in caso di emergenza o durante le fasi di spegnimento, qualora non dovessero funzionare le apposite pompe di circolazione. I parametri che intervengono nelle espressioni dei coefficienti di trasmissione del calore per convezione naturale, come si è visto, sono il numero di Prandtl e il numero di Grashof. Se i moti convettivi avvengono in un volume abbastanza grande, e si può quindi supporre che essi non siano molto influenzati dalla viscosità μ del fluido (in quanto in tal caso la distribuzione delle velocità si può in prima approssimazione ritenere uniforme), è possibile scrivere relazioni in funzione del solo N_Gr (N_Pr)², che non contiene la viscosità.

Il caso di parete verticale, a contatto con il fluido soggetto al campo gravitazionale e a temperatura diversa da quella della parete, è il più facile da trattare. Le varie soluzioni proposte, con le due diverse condizioni di temperatura della parete costante o flusso di calore costante attraverso la parete, concordano infatti molto bene. Ecco ad esempio l'espressione proposta nel 1950 dall'ingegnere tedesco Ernst Rudolph Georg Eckert (1904-2004), per pareti a temperatura costante:

Essa è valida se N_Ra < 5 x 10⁸ e se il N_Nu ottenuto assumendo come dimensione caratteristica D l'altezza della parete, è mediato su tutta la sua superficie. Tale espressione è valida solo se i moti convettivi non provocano turbolenze nel fluido. Per N_Ra >5 x 10⁸, sono state scritte espressioni più complicate, valide per qualsiasi fluido anche non metallico, e a cui si attribuisce una buona corrispondenza con la realtà.

Il reattore nucleare veloce Superphénix di Creys-Malville (Francia)

Prima di cambiare argomento, citiamo l'ultimo di questa lunghissima serie di numeri adimensionali, il cosiddetto numero di Stanton, intitolato all'ingegnere britannico Sir Thomas Edward Stanton (1865-1931). Esso è pari al rapporto tra il numero di Nusselt e il numero di Péclet:

Esso esprime il rapporto tra quantità di calore trasferito e capacità termica del flusso, ma anche il rapporto tra il flusso termico che si realizza ad un'interfaccia e il flusso convettivo di energia termica. In pratica, esso rappresenta l'equivalente per il calore di quello che in Meccanica è noto come coefficiente di attrito.

.

A.4  L'irraggiamento

Quest'ultimo meccanismo di propagazione del calore è analogo a quello della propagazione della luce. Infatti l'irraggiamento avviene sotto forma di onde elettromagnetiche, e in particolare di raggi infrarossi. Mentre nella conduzione e nella convezione del calore quest'ultimo può trasmettersi solo attraverso la materia, per irraggiamento il calore può trasmettersi anche nel vuoto: è grazie a tale meccanismo se il calore irraggiato dal Sole può propagarsi fino alla Terra attraverso il vuoto degli spazi siderali. Qui sotto potete vedere una termografia, scattata dall'autore di questo ipertesto nel Laboratorio del Dipartimento di Energetica del Politecnico di Milano: sulla destra si distingue un tavolo, più caldo del resto del locale. La termografia evidenzia l'emissione infrarossa, e quindi gli oggetti più caldi appaiono rossi, i più freddi appaiono blu.

Quando un oggetto viene investito da radiazione infrarossa, una frazione R dell'energia irradiata viene riflessa, una frazione A viene assorbita e una frazione T viene trasmessa attraverso di esso. Naturalmente dovrà risultare:

R + A + T = 1

• Se R = 1, A = 0 e T = 0 si parla di corpo perfettamente riflettente o di corpo bianco.

• Se R = 0, A = 1 e T = 0 tutto il calore viene assorbito e nulla di esso viene trasmesso; si parla in tal caso di corpo nero.

• Se R = 0, A = 0 e T = 1 si parla di corpo perfettamente trasparente.

Soffermiamoci sul caso del corpo nero: si definisce così un sistema termodinamico in grado di assorbire l'energia di tutte le radiazioni che lo colpiscono, indipendentemente dalla loro frequenza., cosicché a temperatura ambiente esso appare generalmente di colore nero. Tuttavia bisogna fare attenzione a non confondere il corpo nero con il ben più famoso "buco nero"! Infatti, mentre il "buco nero" assorbe tutte le radiazioni che riceve e non emette nulla di suo, al contrario, quando viene riscaldato, il corpo nero si trasforma in un radiatore termico, che emette una radiazione ben precisa, indipendente dalla natura e dalla forma del corpo, che dipende solo dalla temperatura alla quale è portato. Un esempio tipico di corpo nero è infatti rappresentato dal nostro Sole, che è tutt'altro che nero, ed anzi emette una quantità di radiazione straordinaria in ogni secondo!

Un corpo perfettamente nero ovviamente in natura non esiste, così come non esiste un corpo perfettamente bianco (i corpi esistenti in natura sono chiamati anche corpi grigi), però si può modellizzare un sistema ad esso equivalente mediante una bottiglia (o un'altra cavità) annerita con nerofumo sulla superficie esterna, e con un collo molto stretto. La radiazione che raggiunge la superficie esterna viene da essa assorbita per via del suo colore nero, mentre quella che penetra dentro la cavità attraverso il foro ha una probabilità estremamente piccola di riuscire ad uscire dalla stessa via, perchè dopo un gran numero di riflessioni viene completamente assorbita dalle pareti interne prima di riuscire a ritrovare l'uscita:

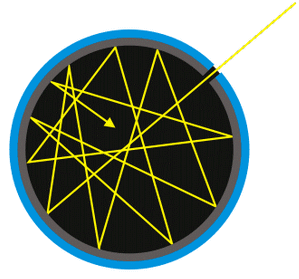
L'emissione totale di un corpo cresce rapidamente all'aumentare della temperatura assoluta; nel caso di un corpo nero, l'energia E emessa dall'unità di superficie nell'unità di tempo su tutte le frequenze, chiamata l'emittanza del corpo nero, è espressa dalla cosiddetta Legge di Stefan-Boltzmann, che prende il nome dal fisico sloveno Josef Stefan (1835-1893) e dal famoso Ludwig Boltzmann (1844-1906), che la elaborarono nel 1879:

E = σ T⁴          (A.15)

In essa, σ è la cosiddetta costante di Stefan-Boltzmann:

σ = 5,67 x 10^–8 W m^–2 K^–4

Vediamo come è possibile ricavare tale relazione dal Primo Principio della Termodinamica, utilizzando gli strumenti dell'Analisi Matematica; chi non li possiede, salti più avanti. Infatti, scrivendo il Primo Principio in forma differenziale, si ha:

dU = d*Q – d*W = T dS – P dV

Dividendo ambi i membri per dV, e ricordando che per le funzioni di più variabili è necessario usare le derivate parziali, si ha:

          (A.16)

Ora, ricordiamo la definizione di energia libera di Helmholtz A data nel § 6.6. Esprimendo la A in termini differenziali, per la (6.14) si ha:

dA = – S dT – P dV

Da essa, tenendo costanti prima il volume (isocora) e poi la temperatura (isoterma), si ricava:

Deriviamo ora entrambi i membri della prima rispetto a V ed entrambi i membri della seconda rispetto a T:

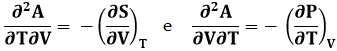
Ora, il Lemma di Schwarz ci dice che le derivate seconde miste sono uguali tra di loro (vedi § 0.3):

di conseguenza lo sono anche i secondi membri delle precedenti. Uguagliandoli e semplificando i segni meno, si ha:

Questa è una delle cosiddette relazioni di Maxwell. Sostituendola nella (A.16), si ha:

Ora, ∂U / ∂V è la densità di energia u, e si dimostra che la pressione P è pari ad 1 / 3 di tale densità di energia. Sostituendo tale relazione nella precedente si ha:

la quale si può riscrivere:

Separiamo le variabili ed otteniamo:

Integrando si ha:

Che si può riscrivere:

Ma si può dimostrare che la densità di energia u è pari ai 4 / 5 dell'emittanza E; ponendo 5 K / 4 = σ si ha proprio la Legge di Stefan-Boltzmann (A.15)!

Variando la temperatura, varia fortemente l'emittanza (se T raddoppia, E aumenta di sedici volte!) e, come è stato dedotto per la prima volta dal fisico tedesco Wilhelm Wien (1864-1928), varia anche la lunghezza d'onda cui corrisponde la massima emittanza. Essa è infatti inversamente proporzionale alla temperatura assoluta secondo la Legge di Wien o Legge dello Spostamento:

          (A.17)

La costante di Wien vale:

b = 2,898 x 10^–3 m K

Siccome dalla lunghezza d'onda di massima emittanza è possibile risalire alla temperatura, la Legge di Wien ha un'importante applicazione in Astrofisica per la misura delle temperature stellari, e in genere di tutti quei radiatori termici che possono essere assimilati ad un corpo nero.

Esempio A.5: La temperatura superficiale del nostro Sole è pari a 5777 K. A quale lunghezza d'onda corrisponde la massima emittanza?

Applichiamo la Legge dello Spostamento (A.17):

Questa lunghezza d'onda corrisponde a una frequenza c / λ = 598 milioni di MegaHertz, cioè alla luce gialla. Ed è per questo che il Sole è descritto come una stella gialla, pur emettendo luce su tutto lo spettro di frequenze!

Esempio A.6: Una fornace per metalli presenta un'apertura di 80 cm². Dall'esame dello spettro di emissione eseguito attraverso l'apertura si ricava che la lunghezza d'onda di massima emittanza è λ_max = 0,7 μm. Determinare la temperatura della fornace e la potenza richiesta per mantenerla a quella temperatura.

Dalla Legge di Wien (A.17) ricaviamo subito:

E grazie alla Legge di Stefan-Boltzmann (A.15) troviamo l'emittanza:

Siccome la potenza è data dal prodotto dell'emittanza E per la superficie S, si ha:

Fornace domestica per metalli (da questo sito)

Il corpo nero ha una grandissima importanza nell'ambito della Fisica Moderna, perchè fu proprio cercando di interpretare correttamente il profilo dello spettro di corpo nero che Max Planck (1858-1947) introdusse per primo l'ipotesi della quantizzazione dell'energia. Ma questa è tutta un'altra storia, e la tratteremo in un altro ipertesto.

.

E con questo, è davvero tutto. Per passare a cimentarvi con gli esercizi conclusivi, che vi diranno se avete compreso o meno i problemi dibattuti in questo ipertesto, cliccate qui. Buona soluzione! Per tornare all'indice, invece, il link è questo.

____