

|
"Ogni atomo è armonizzato con l'immenso universo; e la sua natura dipende dalla natura del tutto. Giova, ad intendere le cose grandi, studiare le piccole. E viceversa." Niccolò Tommaseo (1802-1874) |
.
1.1 Non divisibile
Il concetto di atomo venne introdotto per la prima volta nella storia della Fisica dai filosofi greci del IV secolo a.C. Si ricorda al proposito una celebre disputa tra Aristotele di Stagira (384-322 a.C.) e Democrito di Abdera (460-370 a.C.): i seguaci dell'uno sostenevano che la materia è infinitamente divisibile senza che essa perda le proprie caratteristiche. In altre parole, secondo i seguaci di Aristotele, suddividendo in due un pezzo di ferro si ottengono altri due pezzi di ferro, e continuando a suddividerlo all'infinito si ottengono pezzi di ferro sempre più piccoli, ma dotati di tutte le caratteristiche del ferro. Invece Democrito (il primo ad avere quest'idea però era stato il suo maestro Leucippo di Mileto) sostenne che, continuando a suddividere la materia, si perviene ad un componente più piccolo e non più ulteriormente suddivisibile. Tale componente fu battezzato atomo, dal greco ἄ , "non" (il cosiddetto "alfa privativo"), e τέμνειν, "tagliare", con il significato di "indivisibile". Siccome però le teorie aristoteliche finirono per affermarsi come preminenti nel mondo antico e nel Medioevo (Dante definì Aristotele « il maestro di color che sanno » in Inf. IV, 131),la teoria atomica finì per cadere nel dimenticatoio. A ciò contribuì il fatto che, secondo Leucippo e Democrito, e secondo il loro seguace Epicuro (342-270 a.C.), gli atomi si aggregano e si disgregano casualmente, nel costituire i corpi di materia, e ciò appariva in contrasto con l'opera della Provvidenza, che è centrale sia nel Cristianesimo sia nell'Islam. Non a caso, Dante Alighieri pone il padre dell'atomismo nel Limbo e lo definisce:
« Democrito che 'l mondo a caso pone » (Inf. IV, 136)

|
Busto di filosofo identificato con Democrito, ritrovato nella Villa dei Papiri di Ercolano |
A rispolverare la teoria atomica furono i fondatori della chimica moderna in epoca illuministica, ed in particolare il francese Joseph Louis Proust (1754-1826) e l'inglese John Dalton (1766-1844). Il primo elaborò la cosiddetta:
Legge delle proporzioni definite: gli elementi chimici entrano nei composti secondo proporzioni definite e costanti.
Dalton invece è l'autore della celebre:
Legge delle proporzioni multiple: gli elementi chimici entrano nei composti secondo proporzioni espresse da numeri interi e piccoli.
Ad esempio, non è vero che 12,4 grammi di idrogeno e 3,3 grammi di ossigeno si combinano a formare 15,7 grammi di acqua; è invece vero che 2 grammi di idrogeno si combinano con 16 grammi di ossigeno per formare 18 grammi di acqua. Se parto da 4 grammi di idrogeno, solo due di essi entrano in reazione, e gli altri due restano intonsi. Tutto questo è compatibile solo con l'ipotesi secondo la quale la struttura della materia sia di tipo corpuscolare, cioè che essa non sia continua, come suggerivano gli aristotelici, bensì composta da un gran numero di particelle elementari, troppo piccole perchè le si possa distinguere ad occhio nudo o al microscopio ottico. L'atomicità della materia è considerata una delle prime, grandi scoperte della Fisica moderna.
Ben presto vennero misurate le dimensioni e le masse di questi atomi. Uno dei metodi più semplici consiste nel considerare gli atomi come sferette di raggio r. Prendiamo dell'olio in quantità nota (ad esempio 1 mm3) e lo spargiamo sull'acqua in modo che esso formi uno strato monomolecolare. Per vederlo meglio, lo si cosparge di talco. Quindi si misura la superficie di tale strato; dividendo il volume per la superficie se ne trova lo spessore, cioè il diametro delle molecole. Fu così che si valutò all'incirca r ≈ 10–10 metri. In altre parole, occorrono circa 10 milioni di atomi in fila per coprire la distanza di un millimetro. La distanza di 10–10 m (0,1 nanometri, ovvero 100 picometri) è oggi considerata l'unità di misura delle dimensioni atomiche ed è stata chiamata Ångström (Å), in onore del fisico svedese Anders Jonas Ångström (1814-1874), uno dei padri della spettroscopia. Ad esempio, oggi sappiamo che nella molecola d'acqua la distanza tra il centro dell'atomo di ossigeno e quello di uno dei due atomi di idrogeno è pari a 0,9584 Å).
Conoscendo le dimensioni degli atomi, è possibile anche valutare il loro numero. Vale infatti la:
Legge di Avogadro: ogni mole di tutte le sostanze contiene un numero costante di atomi o di molecole, pari al numero di Avogadro:
NAV = 6,02214 x 1023 molecole / mole
Tale numero è intitolato al chimico piemontese Amedeo Avogadro (1776-1856), che lo propose nel 1811. Poiché una mole di idrogeno atomico ha la massa di 1 grammo, se ne deduce che la massa di un atomo di idrogeno è pari a:
![]()
Dunque gli atomi sono troppo piccoli per essere visti o pesati. Solo in tempi recenti, per mezzo di tecniche olografiche, è stato possibile fotografare gli atomi di un cristallo nella loro disposizione regolare, come mostra l'immagine sottostante, scattata da Franz J. Giessibl della Facoltà di Fisica dell'Università di Regensburg, in Germania.
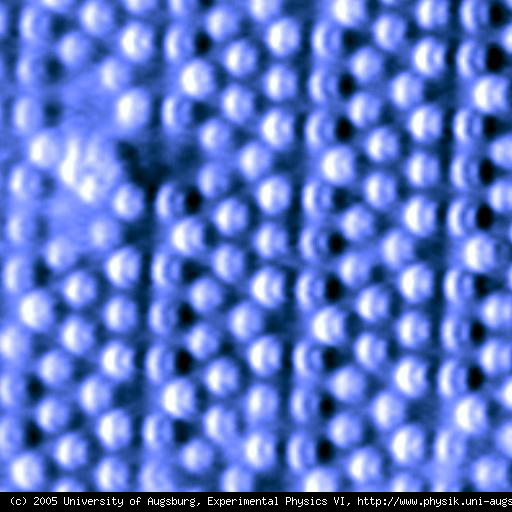
.
1.2 Atomicità dell'elettricità
Mentre i chimici proseguivano le loro ricerche sull'atomo, divenne chiaro che anche l'elettricità ha una natura corpuscolare. La prima idea di una discontinuità all'interno dell'elettricità risale al 1835, nell'ambito degli studi di Michael Faraday (1791-1867) sui fenomeni elettrolitici. Fu lui a stabilire le due leggi dell'elettrolisi:
Prima legge dell'elettrolisi: la massa di una sostanza che si deposita agli elettrodi di una cella elettrolitica è direttamente proporzionale alla quantità di carica che la attraversa.
Seconda legge dell'elettrolisi: se più celle elettrolitiche sono connesse in serie tra di loro, in modo da essere attraversate dalla stessa corrente, le masse di sostanze che si depositano in ogni cella sono proporzionali ai loro equivalenti chimici (cioè al rapporto tra la massa atomica e la valenza dell'elemento).

Michael Faraday (1791-1867) su una banconota britannica da 20 sterline
Sia dunque M la massa di sostanza che si deposita quando nella cella passa la carica q. Se n è il numero di atomi depositati e m è la massa della singola molecola, avremo:
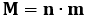
Supponiamo ora che la corrente elettrica sia sostituita da un flusso di particelle, tutte di carica e, che Faraday e gli altri fisici dell'Ottocento supposero inizialmente di carica positiva. La carica q necessaria a depositare n atomi è pari a:
![]()
perchè ogni carica e neutralizza una carica dello ione di quella sostanza, ed ogni ione ha Z cariche (dove Z è la sua valenza). Da qui ricavo:
![]()
e quindi:
![]()
Ma la massa di un atomo è pari al rapporto tra la massa A del grammoatomo e il numero di Avogadro NAV:
![]()
Se ne ricava:
Se considero un elemento, per esempio il rame, A e Z sono costanti, e quindi la massa M che si deposita all'elettrodo è direttamente proporzionale alla carica q che lo attraversa. Se invece fisso la carica q (cioè il prodotto della carica per il tempo) ed ho diversi elettrodi in più celle elettrolitiche collegate in serie, trovo che M è proporzionale al rapporto A / Z, cioè all'equivalente chimico di ogni sostanza. Se ne deduce così che la (1.1) compendia entrambe le leggi di Faraday, e quindi che l'elettricità ha natura atomica, proprio come la materia.
Notiamo che, se q = e NAV, allora la massa di sostanza depositata è pari esattamente al suo equivalente chimico. Ora, l'esperienza ci dice che la carica capace di far depositare una quantità di sostanza pari in grammi all'equivalente chimico, cioè al grammo equivalente, è costante per tutte le sostanze, e vale:
QF = 96.490 Coulomb
Tale valore è pari alla carica di un Faraday (da non confondersi con il Farad, unità di misura della capacità elettrica). Oggi sappiamo che questa costante rappresenta una mole di elettroni (un numero di Avogadro di elettroni). Allora è immediato calcolare il valore della carica elementare:
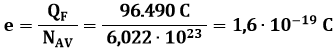

Per sorridere un po' sul numero di Avogadro :)
.
1.3 La scoperta dell'elettrone
Nel 1891 il fisico irlandese George Johnstone Stoney (1826-1911), per indicare questa unità di carica elementare, coniò il termine elettrone. Egli però usava tale termine solo per indicare la carica costante associata nell'atomo a ciascuna unità di valenza; in altre parole, non pensava che si potesse trattare di una particella a sé stante, separata dall'atomo. Chi compì questo passo, rendendosi conto che si trattava di una vera e propria particella subatomica, fu Sir Joseph John Thomson (1856-1940), grazie ai suoi esperimenti con i raggi catodici.
Verso il 1885, ossia due secoli dopo la scoperta della pompa a vuoto ad opera del tedesco Otto von Guericke (1602-1686), il suo connazionale Johann Heinrich Geissler (1814-1879) ideò il modo per realizzare un vuoto spinto all'interno dei recipienti di vetro, ottenendo pressioni fino a 10–4 – 10–5 atmosfere. Questo consentì la realizzazione di opportuni dispositivi costituiti da tubi a vuoto con elettrodi collegati a un generatore di tensione e ad un reostato (cioè ad una resistenza variabile). In seguito il britannico Sir William Crookes (1832-1919) osservò che, collegando gli elettrodi di un tubo a vuoto ad un generatore di alta tensione, l'anodo veniva illuminato da una luce piuttosto intensa proveniente dall'elettrodo negativo. Il tedesco Eugen Goldstein (1850-1930) chiamò queste radiazioni raggi catodici, ma ne ignorava ancora la natura.
Le esperienze successive compiute da Joseph John Thomson dimostrarono che:
a) i raggi catodici si propagano in linea retta, perchè interponendo sul loro cammino un corpo opaco, come una croce di Malta, è possibile vedere la sua ombra sul fondo del tubo (la foto è stata scattata nel laboratorio di Fisica del mio Liceo il 19 dicembre 2022):


b) i raggi catodici sono formati da particelle dotate di massa, perchè sono in grado di far ruotare un mulinello posto tra anodo e catodo:

c) i raggi catodici sono formati da particelle dotate di carica, perchè un campo elettrico e un campo magnetico interposti sul loro cammino li deviano:

Tutto questo bastò a Thomson per affermare che i raggi catodici sono formati da particelle di materia, e non da onde elettromagnetiche come la luce: gli elettroni di Stoney, appunto. Nel 1897 Thomson riuscì a determinare per primo il rapporto fra carica e massa dell'elettrone, usando l'apparato sperimentale illustrato qui sotto:
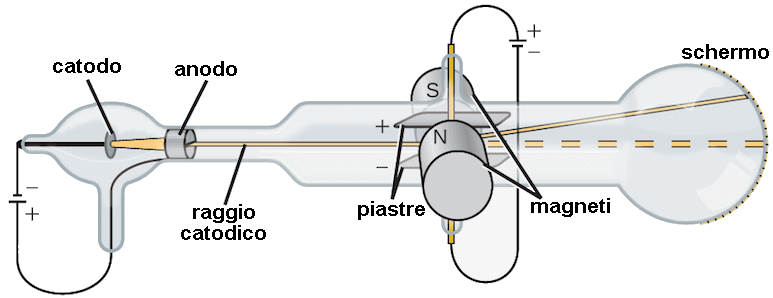
Lungo il cammino dei raggi catodici sono interposti un campo magnetico B e un campo elettrico E, perpendicolari tra di loro. Il primo è costante, prodotto da opportuni strumenti chiamati bobine di Helmholtz, dal nome del loro inventore Hermann von Helmholtz (1821-1894) Invece il secondo è variabile, regolando la d.d.p. tra i due piatti di un condensatore. In figura il campo elettrico è diretto dall'alto verso il basso, per cui l'elettrone è attratto verso l'alto. La forza magnetica è perpendicolare sia alla velocità dell'elettrone che al campo magnetico, quindi è diretta verso il basso, in direzione opposta alla forza elettrica. Inizialmente spegniamo gli alimentatori delle bobine del campo magnetico e lasciamo agire il solo campo elettrico.
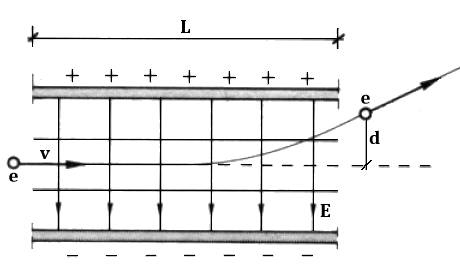
Sia L la lunghezza percorsa dal raggio catodico dentro il campo elettrico; dietro le piastre poniamo una griglia centimetrata che permette di misurare la deflessione d dell'elettrone all'uscita dalle piastre. Finché si trova tra di esse, l'elettrone avverte una forza elettrica pari a FE = e E, e quindi un'accelerazione pari a:
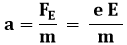
Tale accelerazione è diretta verticalmente, per cui il moto delle particelle si scompone nelle due componenti:
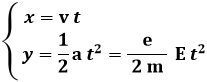
Ricavando il tempo t dalla prima equazione e sostituendolo nella seconda, se ne ricava la traiettoria:
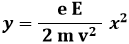
Come si vede, è l'equazione di una parabola. Se, come detto, L è lo spostamento dell'elettrone in orizzontale, e d quello in verticale, si avrà:
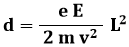
da cui si ricava il rapporto tra carica e massa dell'elettrone:

|
Dispositivo sperimentale per ripetere l'esperienza di Thomson in un laboratorio scolastico. Il campo magnetico è prodotto dalle bobine di Helmholtz, a forma di anello. Nel riguardo si vede la deflessione dei raggi catodici |
Per trovare tale valore però è necessario conoscere la velocità dell'elettrone; com'è possibile, trattandosi di una particella subatomica? Ci riusciremo usando un brillante artificio. Diamo infatti tensione alle bobine che producono il campo magnetico, e facciamo in modo che l'elettrone avverta contemporaneamente un campo magnetico e un campo elettrico. Siccome la forza magnetica e la forza elettrica che l'elettrone avverte hanno uguale direzione ma verso opposto, regolando opportunamente E potremo far sì che la forza elettrica sull'elettrone sia uguale ed opposta a quella magnetica, e in tal modo la deflessione del fascio di raggi catodici tornerà ad essere nulla. Si sa che la forza elettrica vale FE = e E e che quella magnetica (la forza di Lorentz) vale FB = e v B. Uguagliando i moduli delle due forze si ha:
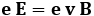
dunque i raggi catodici non vengono deflessi se la loro velocità è pari a:
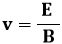
Sostituendo tale valore nella (1.2) si ha:
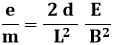
Sostituendo i valori numerici ricavati dall'esperienza si trova che il rapporto fra carica e massa dell'elettrone è pari a:
q / m = 1,75882 x 1011 C / kg
Per tale risultato, Thomson vinse il Premio Nobel per la Fisica nel 1906. Restava però il problema di misurare l'esatto valore della carica dell'elettrone. Il primo che ci riuscì fu Robert Millikan (1868-1953), primo di una lunghissima serie di fisici nati negli Stati Uniti d'America a vincere il Premio Nobel, nel 1923 (Albert Michelson lo aveva già vinto nel 1907 ma egli, pur avendo la cittadinanza americana, era nato in Polonia). Millikan fece uso di un ingegnoso procedimento che ancora oggi stupisce per la sua semplicità e la sua genialità, passato alla storia come l'esperienza di Millikan. Essa, condotta per la prima volta nel 1908, ebbe anche il merito di dimostrare inequivocabilmente la quantizzazione della carica elettrica.

Robert Millikan (1868-1953) e il suo dispositivo sperimentale
Millikan utilizzò due lastre metalliche parallele collegate ai due poli di una batteria, in modo da generare tra di esse un campo elettrico uniforme. Nella lastra superiore era praticato un foro, attraverso il quale venivano spruzzate mediante uno spray, delle minutssime goccioline d'olio che, sfregando tra di loro e contro le molecole d'aria, si caricavano elettricamente. Le gocce venivano osservate tramite un microscopio apposito. In assenza di campo elettrico ogni goccia cade con velocità costante, perchè quando l'attrito dell'aria diventa uguale e opposto alla sua forza peso, sulla goccia non agisce più alcuna forza, e il moto uniformemente accelerato di caduta dei gravi si trasforma rapidissimamente in un moto rettilineo uniforme.
Se carichiamo le piastre in modo che la forza elettrica dovuta al campo elettrico sia uguale e opposta alla forza peso della gocciolina, essa resta ferma a mezz'aria. Invertendo la polarità delle piastre, la forza elettrica cambia verso, diretta verso il basso. Essa si somma allora alla forza peso, che è uguale ad essa in modulo, per cui la forza cui la gocciolina è soggetta raddoppia. Millikan misurò la velocità uniforme con cui la goccia cade in questo secondo caso, verificando che è pari esattamente al doppio di quella che si misurava in assenza di campo elettrico. In tal modo il nostro fisico dimostrò che la velocità con cui si muove la gocciolina si può ritenere con ottima approssimazione direttamente proporzionale alla forza che agisce su di essa, proprio come suggerisce lo studio teorico dell'attrito viscoso dell'aria.
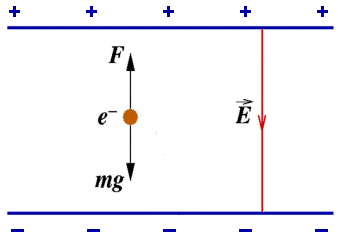
A questo punto, Millikan cambiò la carica elettrica sulla goccia irradiandola con raggi X. A seconda della carica ora presente sulla gocciolina, essa scende verso il basso o sale verso l'alto: nel caso in cui la lastra superiore è carica positivamente, la goccia sale se è carica negativamente, scende se è carica di segno opposto. Misurando la velocità della gocciolina per diversi valori di carica su di essa, Millikan si accorse che tali velocità non erano casuali, ma erano tutte multiple di un valore fondamentale. Questo significa che anche le forze sono tutte multiple di un valore fondamentale; e, siccome F = q E, dove E è il campo elettrico tra le piastre, anche le cariche sulle gocce devono essere multiple di un valore fondamentale. I risultati ottenuti da Millikan dimostrano in modo semplice ma efficace che esiste un'unità granulare di carica, e tutte le cariche elettriche osservate in natura sono multipli interi di tale carica fondamentale, non ulteriormente frazionabile, che rappresenta il quanto di carica elettrica. Tale quanto coincide con la particella che noi chiamiamo elettrone, e oggi sappiamo che la sua carica, stimata da Milliksn, vale:
e = − 1,602176 x 10−19 C
di conseguenza la sua massa vale:
me = 9,109383 × 10−31 kg
Se confrontiamo tale massa con quella degli atomi, da noi stimata nel § 1.1, scopriamo che la massa dell'elettrone è 1800 volte più piccola di quella dell'atomo di idrogeno. Lo stesso Thomson, presentando la sua nuova scoperta al mondo con l'articolo « Cathode Rays » del 7 agosto 1897 (leggetelo a questo link), parlò dell'elettrone come di « un nuovo stato della materia », e quindi come di un'entità subatomica. In altre parole, egli considerò giustamente l'elettrone come uno dei costituenti dell'atomo, il primo ad essere scoperto! Diamo la parola allo stesso Thomson nell'articolo suddetto:
« Thus on this view we have in the cathode rays matter in a new state, a state in which the subdivision of matter is carried very much further than in the ordinary gaseous state: a state in which all matter − that is, matter derived from different sources such as hydrogen, oxygen, &c. − is of one and the same kind; this matter being the substance from which all the chemical elements are built up. »
[Così, da questo punto di vista, nei raggi catodici noi abbiamo materia in un nuovo stato, uno stato in cui la suddivisione della materia è portata molto più in profondità rispetto allo stato gassoso ordinario: uno stato in cui tutta la materia - cioè la materia derivata da sorgenti diverse come idrogeno, ossigeno, ecc. - è di uno e di un solo tipo; e questa materia è la sostanza di cui tutti gli elementi chimici sono costituiti.]

Joseph John Thomson su di un francobollo della Guinea Bissau
.
1.4 Il modello a plumcake
I fisici arrivarono così a comprendere che l'atomo NON è una particella indivisibile, ma anzi è una realtà complessa dotata di una sua struttura interna. Era dunque logico elaborare dei modelli per interpretare i primi sperimentali della nascente Fisica Atomica. In particolare, ogni atomo deve necessariamente contenere al proprio interno gli elettroni di carica negativa, ma deve essere altresì elettricamente neutro, per cui deve contenere almeno altrettanta carica positiva. Siccome però la massa elettronica è quasi duemila volte più leggera della massa atomica, ne consegue che la carica positiva deve essere associata alla stragrande maggioranza della massa dell'atomo.
In base a queste considerazioni, nel 1902 Joseph John Thomson pensò all'atomo come ad una sfera omogenea di carica positiva, nella quale sono immersi gli elettroni come chicchi di uva passa in un plumcake. Per chi non comprendesse questa similitudine, aggiungerò che il plumcake è un dolce tipico inglese a base di farina, uova, zucchero, burro e frutta candita, che nel Regno Unito viene servito tagliato a fette per accompagnare il tè del pomeriggio. Il termine "plumcake" deriva dal fatto che anticamente in Inghilterra al posto della frutta candita si usavano le prugne secche (in inglese "plum"). Questa similitudine ha portato i Fisici a battezzare il modello atomico di Thomson con il nome di modello a plumcake. Dato che questo dolce non fa parte delle tradizioni culinarie della nostra Penisola, nella letteratura scientifica italiana è invalsa la denominazione di modello a panettone, visto che anche nella pasta di questo dolce natalizio l'uvetta e la frutta candita sono disperse uniformemente.
 _____
_____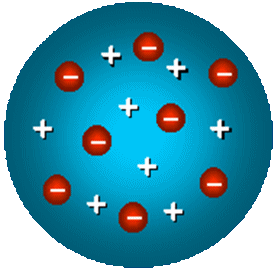
Il numero di elettroni presenti nell'atomo all'equilibrio detto numero atomico Z dell'atomo, per cui la carica positiva e quella negativa equivalgono entrambe a | Z e |. Gli elettroni sono a riposo, sotto la duplice azione della repulsione elettrostatica tra di loro e dell'attrazione da parte del centro delle cariche positive. Supponiamo di considerare un elettrone posto a distanza x dal centro delle cariche positive. Esso avverte l'attrazione di una sfera di carica positiva che ha raggio pari a x; se + Z e è la carica positiva dell'atomo e R è il suo raggio, la densità di carica positiva ρ nell'atomo di Thomson risulta pari a:
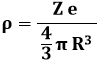
Dunque la carica positiva sottostante l'elettrone è:
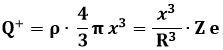
perciò l'elettrone avverte una forza pari a:
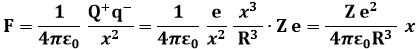
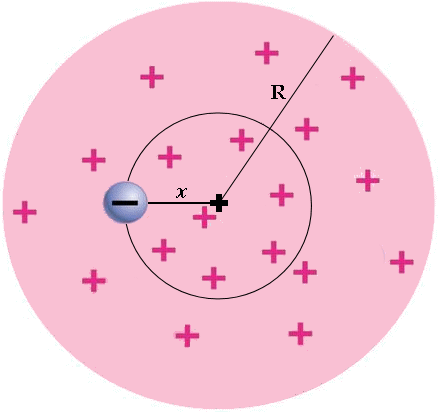
Tale forza è proporzionale alla distanza dal centro dell'atomo, ed è diretta in direzione opposta allo spostamento dell'elettrone dal centro. Insomma, è una forza in tutto simile alla forza elastica! Praticamente è come se, nel modello atomico a plumcake, gli elettroni fossero vincolati tramite molle al centro dell'atomo! Una massa vincolata a una molla, com'è noto, si muove di moto armonico; determiniamone la frequenza di oscillazione. Applicando il Secondo Principio della Dinamica F = m a, si ricava l'accelerazione con cui si muovono gli elettroni:
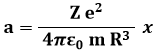
Ma nel moto armonico l'accelerazione a è legata allo spostamento x da questa relazione:
![]()
dove ω è la pulsazione, per cui deve risultare:
![]()
La pulsazione è legata alla frequenza f falla relazione ω = 2 π f; sostituendo i valori numerici si trova che la frequenza f è dell'ordine dei 1015 Hz. Guarda caso, è proprio l'ordine di grandezza della frequenza della luce generata da corpi caldi, che va a formare quelli che chiameremo gli spettri di emissione. Come si vede, pur nella sua semplicità, e volendo nella sua grossolanità, il modello di Thomson è in grado di spiegare l'emissione luminosa da parte dei corpi surriscaldati, e dunque Thomson si è abbondantemente guadagnato il Premio Nobel.
Se però questo modello fosse valido, le frequenze di oscillazione apparirebbero come armoniche successive di una frequenza fondamentale, il che non è vero per nessuna serie spettroscopica. L'unico modo di far combaciare deduzioni teoriche e risultati sperimentali è quello di far ricorso a disuniformità di carica interne all'atomo, il che rende però i calcoli estremamente complessi. Il modello di Thomson rappresenta solo un primo tentativo di interpretare correttamente i dati sperimentali, un tentativo destinato inevitabilmente al fallimento, essendo ancora essenzialmente basato sulla meccanica classica. Ora vedremo come questa difficoltà cominciò a venire aggirata.
.
1.5 Il modello planetario
Sul morire del secolo XIX il fisico francese Henri Becquerel (1852-1902) ed i coniugi Pierre (1859-1906) e Marie Curie (1867-1934) scoprirono quasi contemporaneamente che la materia può emettere tre diversi tipi di radiazioni, che un campo magnetico separa in raggi di carica positiva, raggi di carica negativa e raggi neutri. I primi furono chiamati raggi alfa, i secondi raggi beta e gli ultimi raggi gamma. Attraverso studi successivi, divenne chiaro che i raggi gamma sono onde elettromagnetiche ad altissima frequenza, mentre i raggi beta sono elettroni, sebbene molto energetici (oggi sappiamo che vengono dal nucleo atomico). Quanto ai raggi alfa, essi sono formati da particelle estremamente pesanti, perchè basta un sottile foglio di carta per fermarle, mentre i raggi beta sono fermati solo da un centimetro di metallo, e i raggi gamma solo da uno spesso strato di calcestruzzo! Nel 1909 il fisico neozelandese Ernest Rutherford (1871-1937) e il suo collega britannico Thomas Royds (1884-1955) dimostrarono che le particelle alfa sono in realtà nuclei di elio; oggi sappiamo che sono formati da due protoni e due neutroni, che il nucleo perde quando subisce il cosiddetto "decadimento alfa" (per saperne di più, si legga qui).
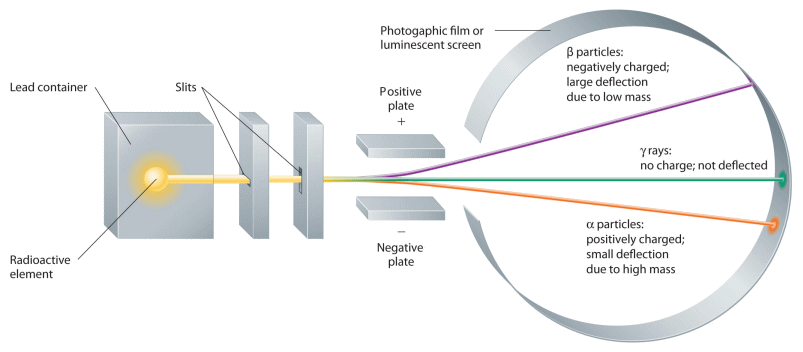
Nel 1909 Ernest Rutherford con i suoi assistenti Hans Wilhelm Geiger (1882-1945, inventore del contatore omonimo) e Ernest Marsden (1889-1970) iniziò una serie di esperimenti sulla diffusione di particelle alfa da parte della materia, oggi noti come esperimenti di Geiger e Marsden. L'apparato sperimentale è quello illustrato qui sotto. In basso a sinistra c'è una sorgente radioattiva (Geiger e Marsden usarono del polonio), contenuta in una scatoletta di piombo munita di un forellino, dal quale fuoriescono le particelle alfa. Il fascio di particelle alfa viene collimato e poi inviato verso una lamina d'oro, così sottile da risultare quasi monoatomica (l'oro è uno dei metalli più malleabili che esistano). Tutt'attorno vi è uno schermo fluorescente, che permette di determinare il numero di particelle diffuse in funzione di quello che viene chiamato l'angolo θ di scattering, cioè l'angolo formato con la direzione di incidenza delle particelle alfa. In genere si tratta di fogli di solfuro di zinco, che emettono scintillazioni quando le particelle alfa le colpiscono, contate mediante un opportuno microscopio.
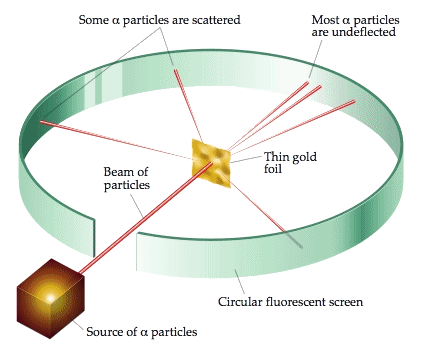
I risultati sperimentali mostrano che le particelle alfa, anziché procedere diritte o quasi, possono essere deflesse anche sotto grandi angoli, fino ad arrivare al cosiddetto "back scattering": alcune particelle cioè possono addirittura essere diffuse all'indietro! Inoltre, l'intensità delle particelle alfa deflesse diminuisce fortemente all'aumentare di θ. Si intuisce subito che la forza responsabile di queste deflessioni è l'interazione coulombiana delle particelle alfa con la distribuzione di carica positiva degli atomi d'oro, perchè gli elettroni sono così piccoli e leggeri da non poter interagire con le particelle alfa, esattamente come le molecole d'aria non possono certo influenzare il moto dei proiettili di una pistola che le attraversano.
A questo punto, è facile verificare che il modello di Thomson non è in grado di spiegare queste deflessioni. In tale modello, infatti, le particelle alfa avvertono la massima forza di attrazione quando esse sfiorano l'atomo, cioè quando la distanza tra la loro traiettoria e il centro dell'atomo coincide con il suo raggio R. Se Z è il numero atomico dell'oro, avremo:
![]()
La variazione Δp di quantità di moto delle particelle alfa si può ottenere mediante il Teorema dell'Impulso, moltiplicando tale forza per il tempo Δt durante il quale essa agisce, cioè il tempo Δt in cui essa "sfiora" l'atomo. Approssimiamo tale tempo con quello impiegato per attraversare lo strato atomico di spessore 2 R:
![]()
da cui:
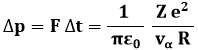
La deflessione si può stimare mediante il rapporto Δp / p:
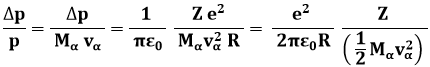
Quella tra parentesi è l'energia cinetica delle particelle alfa. Inseriamo i valori numerici ed esprimiamo l'energia cinetica delle particelle alfa in MegaelettronVolt o MeV (1 MeV = 1,6 x 10−13 J):
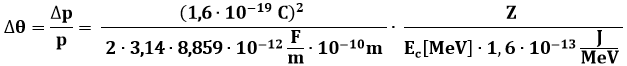
cioè:
![]()
Per l'oro, Z = 79. Se imponiamo Ec = 5 MeV, si ha Δθ ≈ 10−3 rad. Come si vede, una singola interazione tra atomo di Thomson e particelle alfa produce una deflessione di pochi primi d'arco. Per arrivare ad una deflessione di 180° ci vorrebbero migliaia di interazioni, assolutamente improbabili!
In pratica, nel modello di Thomson le deflessioni di particelle alfa sono probabili quanto le deflessioni dei proiettili di fucine sparati contro un covone di fieno: la massa, diluita su tutta la balla, impedisce grandi deflessioni, e dunque ciò che ci aspettiamo è che i proiettili lo attraversino praticamente senza alcuna deviazione. Se vediamo che alcune (poche) pallottole sono deviate di grandi angoli, e certe tornano addirittura indietro, l'unica spiegazione è che vi sia un corpo denso e pesante, ad esempio un ferro da stiro, nascosto dentro il covone, contro il quale le pallottole rimbalzano. Allo stesso modo, la massa della carica positiva diluita nell'atomo di Thomson non può che deflettere debolmente gli elettroni, mentre le deviazioni sarebbero assai maggiori se dentro l'atomo vi fosse un intensissimo campo elettrico, dovuto ad una forte concentrazione di carica al centro di esso. Infatti, nell'espressione di Δp / p calcolata sopra, l'unico modo per aumentare Δθ consiste nel diminuire R, essendo costanti tutti gli altri parametri. Per ottenere un Δθ dell'ordine di un radiante, bisogna ridurre R di almeno cinque ordini di grandezza!
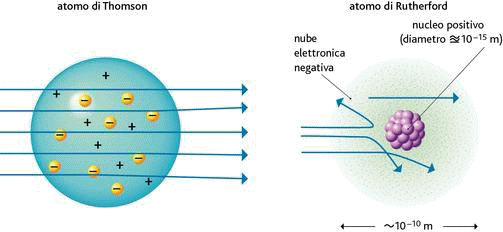
Non si può dunque continuare a pensare all'atomo come una distribuzione uniforme di carica positiva. Al centro di esso deve essere presente una piccola sfera, nel quale è concentrata tutta la sua carica positiva. Rutherford immaginò che dentro l'atomo fosse presente un NUCLEO del raggio di 10−14 − 10−15 metri, nel quale è concentrata tutta la carica positiva e tutta la massa dell'atomo, mentre il resto è praticamente vuoto; gli elettroni non sono più dispersi nella carica positiva, come pensava Thomson, ma ruotano attorno al nucleo secondo orbite circolari, come i pianeti attorno al Sole. Questo prende il nome di modello planetario dell'atomo (1911). La teoria che sta alla base degli esperimenti di scattering come quello di Geiger e Marsden prevede la determinazione della sezione d'urto, definita come il rapporto tra il numero di particelle che vengono deviate nell'angolo solido considerato in un secondo e il numero di particelle che in un secondo attraversano l'unità di superficie. Essa rappresenta quindi la probabilità che una particella alfa di energia cinetica Ec venga deflessa di un angolo θ rispetto alla direzione iniziale, interagendo con una carica pari a + Z e (la carica del nucleo). La sezione d'urto si misura in metri quadrati, anche se, avendo a che fare con superfici piccolissime, si preferisce usare il barn (dall'inglese "barn", "fienile"), pari a 10−24 cm2. Usando gli strumenti dell'Analisi Matematica si può dimostrare che la sezione d'urto σ(θ) in funzione dell'angolo θ è data dalla formula:
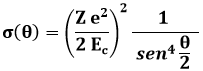
dove Z è il numero atomico del bersaglio e Ec è l'energia cinetica delle particelle alfa. Si parla in proposito di scattering coulombiano. In realtà, se θ vale zero, la sezione d'urto tenderebbe all'infinito, eventualità che nella realtà non si verifica, come mostra la distribuzione sperimentale ottenuta da Geiger e Marsden (N / s è il numero di nuclei arrivati al rivelatore nell'unità di tempo):
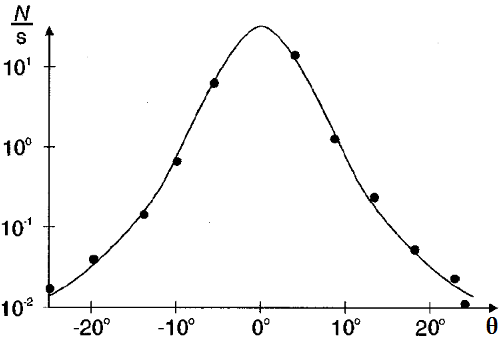
Le dimensioni del nucleo sono misurate di solito in femtometri, dove 1 fm = 10−15. Per ragioni storiche, a quest'unità di misura si dà il nome di Fermi. il raggio nucleare dell'oro stimato da Rutherford valeva 6,9 x 10−15 m, cioè 6,9 Fermi. Ciò significa che l'atomo è quasi completamente vuoto! Per fare un paragone, se il nucleo fosse grande come un pallone, l'intero atomo sarebbe grande come un campo da calcio; e se il nucleo dell'atomo di oro avesse le stesse dimensioni del Sole, la distanza tra il nucleo e l'elettrone più esterno sarebbe doppia di quella che separa il Sole e Plutone!
Un ultimo paragone con il mondo macroscopico ci aiuterà a capire meglio le ridotte dimensioni del nucleo atomico rispetto all'intero atomo. Il pianeta Terra ha un raggio medio di 6370 km; se un atomo crescesse fino alle dimensioni della Terra, quanto risulterebbe grande il suo nucleo? Una semplice proporzione ci porta al valore di 128 metri, che curiosamente è molto simile all'altezza del Buddha Zhōngyuán (中原大佛, "Grande Buddha della Pianura Centrale"), una statua colossale rappresentante il Buddha, posta nella contea di Lushan, nella Cina centrale (provincia di Henan). Fino al 31 ottobre 2018 essa è stata la statua più alta del mondo. Si noti che il "vero" nucleo terrestre, cioè il più interno degli strati di cui è composto il nostro pianeta, ha invece un raggio di 3500 km, ben diverso (in proporzione) da quello del nostro nucleo atomico!

Il Buddha Zhōngyuán di Lushan (Cina)
Chiudiamo questo primo capitolo con una bella poesia dedicata, a sorpresa, proprio all'atomo, scritta da Alberto Cavaliere (1897-1967) e contenuta nella sua ormai classica raccolta intitolata "H2O Chimica in versi":
« Si sa che l'atomo / è il fondamento, / la parte minima / d'un elemento, / i cui caratteri / però - s'osservi - / inalterabili / sempre conservi. / Già indivisibile, / invece adesso / si può dividere / l'atomo stesso / in ben più piccole / parti le quali / hanno caratteri / loro speciali, / che differiscono / dall'elemento / dopo.... chiamiamolo / lo smembramento. / Trovi nell'atomo, / in generale, / un nucleo atomico / (parte centrale), / ed un involucro / che d'ordinario / corteccia chiamasi, / o planetario. / Il nucleo atomico / di cui s'è appreso / e a cui dell'atomo / si deve il peso, / di piccolissime / parti s'avviva, / di cui la carica / è positiva / - parti che soglionsi / chiamar protoni - / e di particole / neutre: i neutroni / (questi derivano / da un elettrone / accomunatosi / con un protone). / Hanno i corpuscoli / del planetario / invece, elettrico / segno contrario: / son quei corpuscoli, / detti elettroni, / che intorno al nucleo / e ai suoi protoni / perenni girano, / come or si sa, / a una incredibile / velocità. / In questo involucro, / a lor legati, / posson distinguersi / parecchi strati, / dei quali l'ultimo, / meglio, il più esterno, / è importantissimo / se ben discerno, / perché determina / a suo talento / le virtù chimiche / dell'elemento. / Il nucleo atomico / è, viceversa, / con metamorfosi / più che perversa, / il responsabile / della "fissione", / in altri termini / la reazione / or non più chimica / ma nucleare: / la bomba atomica / sta per sbocciare... »
E con questo, il primo capitolo è concluso. Fino a qui, infatti, si poteva arrivare utilizzando la Meccanica Classica. Per andare oltre, occorre usare un nuovo tipo di fisica, la Fisica dei Quanti. Per passare con me all'introduzione a tale novo tipo di Fisica, cliccate qui. Per tornare all'indice, invece, il link è questo.
