

|
"Dio regola i fenomeni con la Fisica Classica il lunedì, il mercoledì e il venerdì, mentre il diavolo li regola con la Fisica Quantistica il martedì, il giovedì e il sabato." William Lawrence Bragg |
.
4.1 La crisi del modello quantomeccanico
Dal 1913 al 1926 la teoria di Bohr-Sommerfeld, di cui abbiamo parlato nel capitolo precedente, rappresentò lo schema fondamentale per cercare di interpretare il funzionamento del mondo atomico. Tuttavia, nonostante parecchi brillanti, successi, sotto molti aspetti essa lasciò i fisici del tutto insoddisfatti. Infatti i teorici incontrarono parecchie difficoltà ad estendere la teoria ai sistemi più complessi dell'atomo di idrogeno, ad interpretare la struttura fine degli spettri, e a giustificare le mille regole di quantizzazione introdotte al solo scopo di giustificare le mille regole di quantizzazione introdotte al solo scopo di dare una giustificazione ai fatti sperimentali.
Ma il neo più grosso del modello di Bohr-Sommerfeld era rappresentato dal fatto che, mentre per definire l'equilibrio degli elettroni sulle loro orbite si utilizzavano le classiche leggi della meccanica e dell'elettromagnetismo, queste leggi vengono poi accantonate per ipotizzare invece che l'energia sia quantizzata, e che gli elettroni possano ruotare solo su particolari orbite. Per questa mescolanza un po' illogica, il modello fu detto quantomeccanico, ma già Ernest Rutherford nel 1913 fece notare che questa compresenza di due fisiche letteralmente incompatibili fra di loro rappresentava la maggior debolezza del nuovo modello atomico. A questo proposito, leggiamo un estratto della lettera che Rutherford scrisse a Bohr il 20 marzo 1913, tratto dal fondamentale testo "I quanti e la vita" di Niels Bohr (1963):
« Caro dottor Bohr, ho ricevuto il Suo lavoro e l'ho letto con grande interesse, ma mi riservo di rivederlo con cura non appena ne avrò il tempo. Le Sue idee sull'origine dello spettro dell'idrogeno sono molto ingegnose e sembrano funzionare bene; ma la mescolanza delle idee di Planck con la vecchia meccanica consente molto difficilmente di formarsi un'idea fisica della base di tutto il discorso. Mi sembra ci sia una grave difficoltà nelle Sue ipotesi, che non penso affatto le sia sfuggita: come fa un elettrone a decidere con quale frequenza deve vibrare quando passa da uno stato stazionario all'altro? Sembra che si debba supporre che l'elettrone sappia in partenza dove andrà a finire... »
E non è tutto. William Lawrence Bragg (1890-1971) si spinse ancora più in là, affermando:
« Dio regola i fenomeni con la Fisica Classica il lunedì, il mercoledì e il venerdì, mentre il diavolo li regola con la Fisica Quantistica il martedì, il giovedì e il sabato! »
Occorreva dunque cercare di fondere entrambe le fisiche in una teoria più generale. Del resto, cominciava a farsi strada l'idea che la fisica (per così dire) "macroscopica" non potesse venire estesa in modo automatico al mondo microscopico, perchè gli atomi, gli elettroni, i quanti, ecc. sono completamente differenti dai corpi macroscopici. La teoria di Bohr-Sommerfeld, nata per risolvere i problemi posti dalla vecchia spettroscopia, rappresentava piuttosto un tentativo di introdurre nella Fisica Classica alcune "scappatoie" e "correzioni", mantenendo però inalterato l'edificio generale. Perchè mai l'elettrone non irraggia, se si muove lungo particolari orbite? Questo la vecchia meccanica classica non lo spiegava, e la teoria quantomeccanica lo poneva come un assioma, esattamente come Galilei poneva in modo assiomatico che la Terra ruoti attorno al Sole, senza conoscere i motivi all'origine di questa rivoluzione (e cioè la forza di gravitazione nucleare di Newton). Le difficoltà non nascevano da un formalismo incompleto, bensì dalle stesse basi teoriche su cui l'edificio della Fisica era stato costruito. Le difficoltà erano profonde e di ordine concettuale. Come la Relatività Ristretta di Albert Einstein, nata dalla revisione di alcuni concetti relativi allo spazio ed al tempo, contiene la Meccanica Classica come caso particolare, per velocità molto più piccole di quella della luce, così da una sistematica revisione della fisica quantomeccanica si sperava di giungere a costruire una nuova Meccanica, che potesse giustificare i risultati sperimentali nelle applicazioni microscopiche, e tendere alla Fisica Classica per i fenomeni nei quali scompaiono le discontinuità rappresentate dalla costante h di Planck.
La via per arrivare a formulare una nuova meccanica, detta Meccanica Quantistica, iniziò nel 1924 con la tesi di laurea del francese Louis Victor de Broglie (1892-1987), Accademico di Francia, intitolata « Recherches sur la théorie des quanta ». Grazie a lui, divenne possibile giustificare molti fenomeni microscopici, prima interpretati solo empiricamente, o condizionati da ipotesi ad hoc.
Louis-Victor de Broglie (Dieppe, 15 agosto 1892 – Louveciennes, 19 marzo 1987)
Per interpretare l'effetto fotoelettrico, Albert Einstein aveva abbandonato per primo l'ipotesi puramente ondulatoria della luce, sostenendo che l'energia da essa trasportata non è uniformemente distribuita su tutto il fronte d'onda della radiazione, bensì concentrata in "pacchetti" discreti, detti fotoni o quanti di luce. In tal modo un fascio di onde elettromagnetiche di lunghezza d'onda λ e frequenza f = c / λ, è caratterizzata da un flusso di fotoni di energia h f = h c / λ, che interagiscono con gli atomi della superficie metallica, facendo sì che essa liberi elettroni. Dunque, nei confronti di certi fenomeni la luce si comporta come onda, e nei confronti di altri come un fascio di particelle: è la rivincita di Newton su Huygens. Si parla al proposito di teoria corpuscolo-ondulatoria della luce.
Questo fatto ci costringe ad introdurre una delle più grosse novità della Fisica del Novecento: il dualismo tra onda e corpuscolo. Le radiazioni elettromagnetiche presentano una doppia natura, come il dottor Jekyll e mister Hyde di un celebre racconto di Robert Louis Stevenson: alcuni fenomeni, come la diffrazione e l'interferenza, sono spiegabili solo ammettendo nella luce una natura ondulatoria, mentre altri, come l'effetto fotoelettrico e l'effetto Compton, nonché la produzione di raggi X, fanno pensare piuttosto ad una natura corpuscolare. Circostanza fondamentale di questo sconcertante dualismo è il fatto che in nessun fenomeno è necessario far intervenire contemporaneamente l'aspetto corpuscolare e quello ondulatorio della radiazione. I due modelli, pur partendo da diverse ipotesi, non si escludono a vicenda, ma sono piuttosto complementari, cosicché la radiazione, a seconda del fenomeno in osservazione, presenta ora l'uno ora l'altro aspetto. È come se si osservassero le due facce di una stessa moneta: quando si guarda l'una non si vede l'altra, e viceversa. Qui si coglie subito uno degli aspetti fondamentali della nuova Fisica: la natura dell'osservabile dipende dal tipo di osservazione, e la influenza in modo decisivo. In genere, l'aspetto corpuscolare diventa più evidente ad alte frequenze, cioè quando, aumentando l'energia e la quantità di moto della radiazione, il carattere fotonico diventa sempre più evidente. Il modello ondulatorio domina invece alle basse frequenze (come quella della luce), quando si manifestano maggiormente l'interferenza e la diffrazione. Nel campo delle piccole frequenze (radioonde), la discontinuità energetica delle radiazioni non è minimamente avvertita, mentre diventa dominante nello spettro X e gamma.
Solo nel 2015 i ricercatori del Lumes (Laboratoire pour la microscopie et la diffusion d'électrons) del Politecnico di Losanna coordinati dall'italiano Fabrizio Carbone (1976-) hanno dimostrato che il comportamento ondulatorio e quello corpuscolare della luce possono essere rilevati contemporaneamente e nello stesso sistema fisico, mostrando insieme la doppia natura della luce: onde e fotoni catturati contemporaneamente (tra l'altro il 2015 era l'Anno Internazionale della Luce). Il sistema utilizzato dal team svizzero era costituito da un cavo metallico di dimensioni nanometriche bersagliato da un impulso laser. L'energia del laser veniva trasferita alle particelle, che facevano vibrare il cavo, e allo stesso tempo permetteva alla luce di propagarsi in forma di onde lungo il cavo, in due direzioni opposte. Quando le onde si sommavano, si generava un'onda stazionaria, ossia una sorgente di luce che irradiava attorno al cavo. Il team ha diretto in prossimità del nanocavo un fascio di elettroni: questi hanno interagito con la luce stazionaria, con il risultato di vedere variata la loro velocità. Il microscopio elettronico ha rilevato i rallentamenti e le accelerazioni degli elettroni, mostrando il fenomeno ondulatorio dell'onda, come si vede nella foto sottostante. L'insieme di tutti gli elementi dell'esperimento ha dunque dimostrato la coesistenza di fotoni (che interagivano con gli elettroni) e di onde (che generavano l'onda stazionaria capace di interferire con la velocità degli elettroni). Presentando i risultati del suo esperimento, Fabrizio Carbone ha commentato: « Per la prima volta siamo stati in grado di filmare la meccanica quantistica e la sua natura paradossale! »

Questa alternativa onda-corpuscolo, già acquisita per quanto riguarda le radiazioni elettromagnetiche, non era però mai stata ipotizzata per la meccanica dei corpi materiali. Una particella di materia, per quanto piccola, era sempre stata percepita solo come un corpuscolo, mai come un'onda. Questo fino al 25 novembre 1924 (una data da segnare in rosso sul calendario della Fisica!) quando, come anticipato, con il coraggio intellettuale tipico dei giovani, Louis Victor de Broglie discutendo la sua tesi di laurea (che potete leggere integralmente a questo link) avanzò l'ipotesi sconvolgente che il dualismo onda-corpuscolo rappresentasse un fatto generale nell'universo, e cioè che anche le particelle materiali, in determinate condizioni, manifestino delle caratteristiche ondulatorie. Anche oggetti come elettroni, protoni e atomi, universalmente riconosciuti come corpuscoli materiali, presenterebbero dunque il tipico comportamento ondulatorio di interferenza e diffrazione.
Questo concetto all'epoca suonò come veramente rivoluzionario perché, sino a quel punto, nessuna esperienza aveva mai messo in luce un comportamento di questo genere. Pur tuttavia vi erano diversi motivi a carattere teorico che potevano dar ragione a de Broglie, a partire dall'evidente analogia tra ottica geometrica e meccanica del punto materiale (ad esempio i raggi di luce si propagano in linea retta, proprio come le particelle non soggette a forze), il che poteva condurre ad una seconda analogia tra l'ottica fisica ed una sorta di "meccanica ondulatoria", fino ad allora mai formulata da alcuno. Inoltre, l'introduzione dei numeri interi per giustificare la quantizzazione degli stati stazionari dell'atomo di idrogeno, che in precedenza ci era apparsa solo come un'ipotesi artificiosa per giustificare i risultati sperimentali, avrebbe potuto diventare più logica e naturale se l'elettrone avesse assunto anche un carattere ondulatorio, dal momento che, come sappiamo, le limitazioni espresse da numeri interi appaiono spesso in diversi fenomeni ondulatori, come l'interferenza, la risonanza e le onde stazionarie.
Peraltro, come sappiamo, l'esperimento della doppia fenditura di Young ha aperto alla dimostrazione della natura ondulatoria della luce nell'ambito della fisica classica, ma è stato sfruttato anche per dimostrare il dualismo onda-particella nell'ambito della fisica quantistica. Nella versione classica dell'esperimento di Young, la luce emessa da una sorgente viene diretta verso un pannello con due fenditure sottili, parallele e molto vicine tra loro. Quando la luce attraversa le fenditure, queste ultime si trasformano a loro volte in sorgenti coerenti di luce, producendo su uno schermo una figura di interferenza, composta da strisce di luce chiare alternate a strisce scure), tipica della propagazione di onde. Molti scienziati hanno intuito le potenzialità di indagare il comportamento della luce (e più in generale delle onde) in materiali che presentino una variabilità nel tempo, anziché nello spazio, delle loro caratteristiche: per ottenere tale proprietà, è necessario ricorrere ai cosiddetti metamateriali, ossia materiali artificiali con proprietà elettromagnetiche peculiari che li differenziano dagli altri materiali. Nel 2022 un gruppo di ricerca guidato da Riccardo Sapienza dell'Imperial College London ha avuto l'idea di realizzare una versione temporale dell'esperimento della doppia fenditura, studiando la propagazione della luce non attraverso due fenditure spaziali, ma tramite due fenditure “temporali”, intese come due configurazioni diverse del materiale con cui la luce interagisce. Per questo hanno utilizzato un metamateriale basato su un ossido di indio-stagno, le cui proprietà ottiche possono variare per un brevissimo periodo di tempo dell'ordine del femtosecondo (10–15 s) se sottoposte a un forte impulso laser: la conseguenza è che la luce in arrivo in questo brevissimo lasso di tempo interagisce con il materiale in modo diverso rispetto alla configurazione in cui il laser è spento, proprio come se attraversasse due diverse fenditure nel tempo. Il risultato dell'esperimento è stata l'osservazione di una figura di interferenza prodotta dalla separazione temporale tra le due onde di luce. A differenza dell'interferenza prodotta dalle fenditure spaziali, che si traduce in una variazione angolare delle onde luminose, in questo caso l'interferenza è visibile in una variazione delle frequenze. Le fenditure temporali, insomma, modificano la frequenza della luce, e quindi il suo colore: la figura di interferenza risultante esalta alcuni colori, annullandone altri. Il risultato, oltre a dimostrare il dualismo onda-particella, può costituire un punto di partenza verso applicazioni interessanti, sia di tipo tecnologico sia nell'ambito della fisica fondamentale. Per esempio, un'onda che interagisce con un materiale variabile nel tempo può essere amplificata, con ovvi vantaggi pratici: si può modulare un segnale in frequenza, con possibili applicazioni nel campo delle comunicazioni e della computazione analogica. Sarà interessante in futuro testare questo comportamento anche nei cosiddetti "cristalli temporali", strutture che si ripetono periodicamente nel tempo, teorizzate in anni recenti.
.
4.2 Le equazioni di de Broglie
L'idea base di de Broglie richiede che ad ogni corpuscolo venga associata un'onda, detta onda di materia, con lunghezza d'onda pari a:
Al posto di λ si può usare il cosiddetto numero d'onda, così definito:
Da cui è facile ricavare:

Dalla (4.1) segue dunque la quantizzazione della quantità di moto, così come accadeva nell'atomo di Bohr. λ è il "periodo spaziale" dell'onda di materia, ma se ne può introdurre anche un "periodo temporale" T e una pulsazione ω così definita:
![]()
Essa è del tutto analoga alla (4.2). Il postulato di Planck E = h f ci dice allora che l'energia associata all'onda di materia è:
![]()
Ho così le due equazioni di de Broglie:
Esse ci dicono che ad una particella materiale di energia E e quantità di moto p si associa un'onda di materia di lunghezza d'onda e frequenza date da:
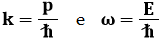
L'equazione più generale di quest'onda di materia è la seguente (ne faremo uso nel capitolo 5):
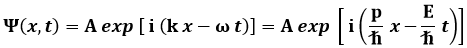
Questa è l'espressione di un'onda piana monocromatica, dotata cioè di una sola frequenza e di una sola lunghezza d'onda. Ad ogni particella materiale è perciò associato un campo continuo.
Proviamo ora ad applicare l'idea di de Broglie al modello quantomeccanico di Bohr-Sommerfeld, e vediamo se le sue ipotesi sono giustificate. Si è visto che l'elettrone nell'n-esima orbita di Bohr ha un raggio dato dalla (3.4):
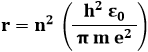
Ma nell'orbita classica la forza centrifuga deve equilibrare la forza elettrostatica, per cui:

da cui:
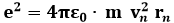
Sostituisco nella precedente ed ho:
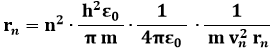
che si può riscrivere così:
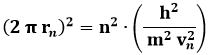
Estraiamo la radice quadrata di ambi i membri:
Se h / m vn rappresenta la lunghezza d'onda di de Broglie λ associata all'elettrone sull'n-esima orbita di Bohr, essa si può così riscrivere:
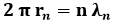
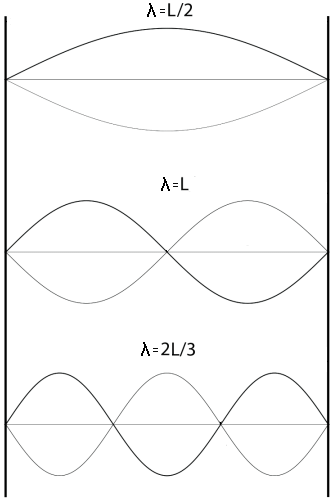
Questo significa che l'n-esima orbita di Bohr contiene n oscillazioni complete, e quindi che le onde di de Broglie associate alle orbite di Bohr sono stazionarie, come mostra la figura sottostante:
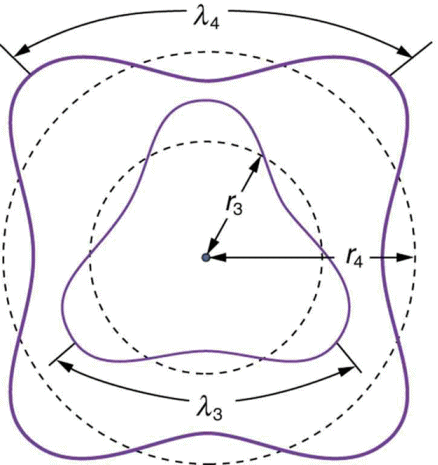
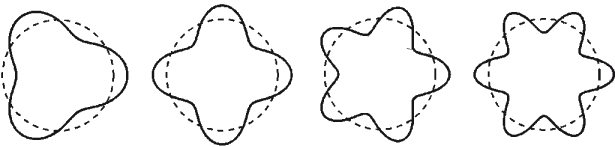
Le "onde pilota" associate agli elettroni di un atomo non possono dunque che avere delle particolari lunghezze d'onda, se vogliono essere stazionarie, altrimenti così non potrebbe essere. Questo è esattamente ciò che accade ad un'onda intrappolata tra due specchi paralleli: essa può vibrare solo se la sua lunghezza d'onda è un sottomultiplo intero della distanza tra gli specchi medesimi. Nel caso dell'atomo, la "scatola" tra i cui specchi l'onda si riflette è una buca di potenziale rappresentata dall'attrazione elettrostatica del nucleo!
Notiamo che la (4.5) può essere così riscritta:
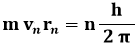
E questa, come abbiamo visto, coincide con l'ipotesi di Bohr (3.3) alla base del suo modello atomico! Perfino il 2 π, che ci sembrava comparso quasi per magia, trova piena giustificazione grazie all'ipotesi avanzata da de Broglie.
4.3 La diffrazione degli elettroni
Fin dalle prime esperienze di Bragg sulla diffrazione dei raggi X fu evidenziata la regolare struttura dei cristalli, caratterizzati da una distanza tra i piani reticolari dell'ordine di 10–10 metri. Questo fatto indusse i fisici sperimentali a cercare una verifica sperimentale delle onde di de Broglie utilizzando i cristalli come reticoli di diffrazione. La prima verifica di questo tipo fu effettuata nel 1927 dagli americani Clinton Joseph Davisson (1881-1958) e Lester Halbert Germer (1896-1971) presso i Bell Labs dove lavoravano, ed è passata alla storia con il nome di esperienza di Davisson e Germer.
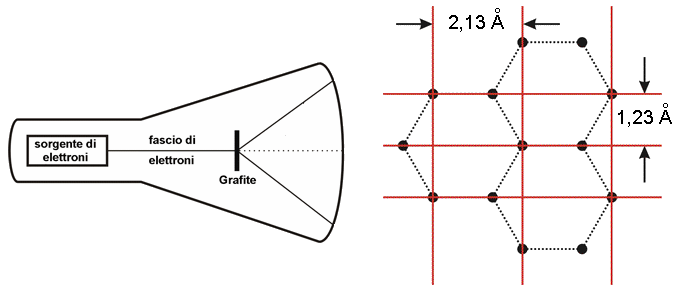
Essi utilizzarono un dispositivo che generava fasci di elettroni, e li fecero incidere su un sottile reticolo policristallino di grafite. Di fronte alla grafite è posto uno strato di sostanza fluorescente. Su di esso si ottengono degli anelli, molto simili a una figura di diffrazione; al centro si nota una macchia luminosa, dovuta agli elettroni che attraversano la grafite senza essere diffratti, circondata da vari anelli. I singoli cristalli del foglio policristallino hanno una struttura esagonale, come si vede in figura, ma possono assumere tutte le possibili angolazioni, cosicché i raggi diffratti sui vari cristalli formano delle superfici coniche aventi come assi di simmetria la direzione del fascio incidente di elettroni; le loro intersezioni con lo schermo sono dunque rappresentate proprio da anelli!
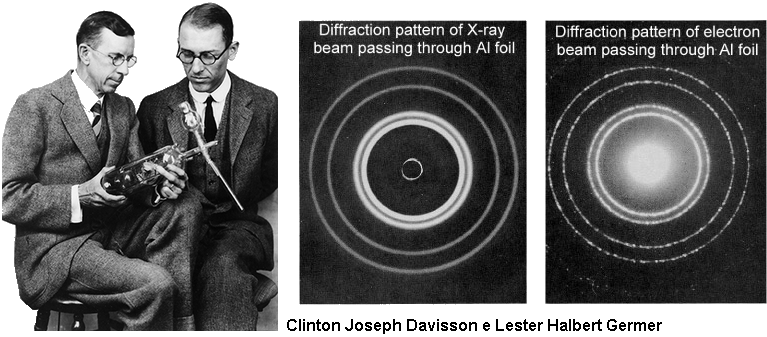
Si osservano in particolare due anelli di diffrazione, dovuti ad una particolarità dei cristalli di grafite, dotati di due sistemi di fasci piani paralleli tra di loro. La distanza tra i piani di un fascio assume valori diversi, a seconda del fascio considerato. A questo punto è facile capire come le onde associate agli elettroni siano riflessi dai nostri piani reticolari e, se soddisfano alla cosiddetta condizione di Bragg:
2 d sen θ = n λ (n = 1, 2, 3...=
allora si hanno massimi di diffrazione. Rappresentiamo due onde appartenenti allo stesso fascio, che si riflettono su due piani reticolari paralleli. Se θ è l'angolo che la direzione di propagazione dei raggi incidenti forma con la giacitura dei piani reticolari, la differenza di cammino tra le due onde in figura è AI' + I'B, pari a 2 d sen θ, dove d è la distanza fra i piani reticolari:
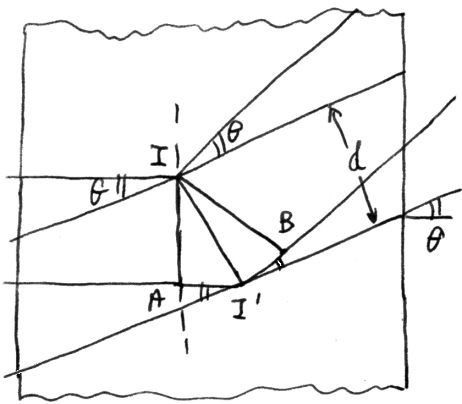
Com'è noto, si ha interferenza costruttiva se la differenza dei cammini ottici è un multiplo intero della lunghezza d'onda λ, cioè:
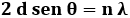
che proprio la condizione sopra scritta. In particolare se n = 1 ho 2 d θ = λ, dove si è usata l'approssimazione sen θ ≈ θ per piccoli angoli. Ciò consente di valutare la distanza d dei piani reticolari nota la lunghezza d'onda λ, che si ricava dalle equazioni di de Broglie. Se infatti V è il potenziale che accelera gli elettroni, si ha:
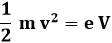
giacché tutta l'energia potenziale si è trasformata in energia cinetica. Da qui ho:
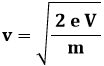
e quindi:
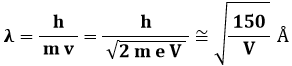
Questo consente la misura delle due costanti reticolari della grafite. Il maggior risultato ottenuto da Davisson e Germer fu comunque quello di dimostrare che gli elettroni hanno realmente proprietà ondulatorie, e che la lunghezza d'onda ad essi associata è precisamente quella prevista da de Broglie. Intorno al 1930, il tedesco Otto Stern (1888-1969) ripetè lo stesso esperimento usando stavolta atomi di sodio al posto di elettroni, e dimostrando che anch'essi possiedono proprietà ondulatorie, perchè diffrangono!
A questo punto, sorge spontanea una domanda: come mai elettroni ed atomi diffrangono attraverso un reticolo cristallino, ma noi NON diffrangiamo attraverso le porte, o una palla da basket non diffrange attraverso il canestro in cui cade? Il cuore del problema sta nella piccolezza della costante di Planck. Calcoliamo la lunghezza d'onda di de Broglie associata ad un elettrone avente velocità v = 106 m / s:

Essa è quindi dell'ordine delle dimensioni atomiche, per cui l'elettrone diffrange attraverso i reticoli cristallini, esattamente come fanno i raggi X. Invece, una palla da basket di massa pari a 600 g e velocità di 1 m / s ha una lunghezza d'onda di de Broglie pari a:
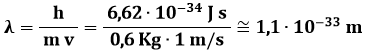
che è di 32 ordini di grandezza più piccolo del canestro regolamentare! Siccome il fenomeno della diffrazione avviene solo se la lunghezza d'onda ha lo stesso ordine di grandezza della fenditura o del passo reticolare, ne segue che non esiste un canestro così sottile da permettere la diffrazione delle palle da basket! Per esse, dunque, si potrà tranquillamente adoperare il formalismo della Meccanica Classica, non comparendo mai effetti quantistici. Non è così invece per le particelle elementari, per le quali : esse abbisognano di una nuova meccanica, che sarà detta per l'appunto Meccanica Ondulatoria.
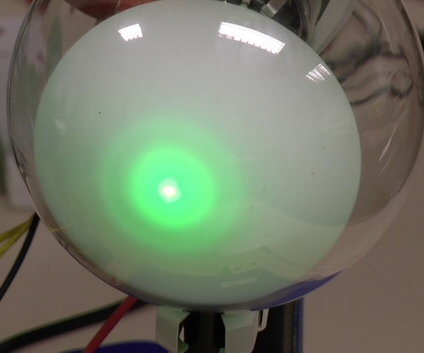
Diffrazione di elettroni in un laboratorio scolastico
.
4.4 Il microscopio elettronico
Il dispositivo che, ancor oggi, rappresenta la più importante applicazione pratica delle idee di de Broglie è certamente il microscopio elettronico. Il primo fu costruito in Germania negli anni trenta, subito dopo la scoperta delle lenti elettroniche a deflessione magnetica, ad opera del fisico tedesco Hans Busch (1884-1973). Nel 1928 il fisico ungherese Leó Szilárd (1898-1964), uno degli epigoni dell'era atomica, propose a Busch di fabbricare un microscopio elettronico, per il quale aveva ottenuto un brevetto. Tuttavia i primi a mettere a punto un microscopio elettronico da quattrocento ingrandimenti nel 1931 furono altri due tedeschi, il fisico Ernst Ruska (1906-1988) e l'ingegnere elettronico Max Knoll (1897-1969). Due anni dopo Ruska costruì il primo microscopio elettronico con risoluzione maggiore di quella massima ottenibile con un analogo strumento ottico. Nel 1937 Manfred von Ardenne (1907-1997) sperimentò il microscopio elettronico a scansione. Il primo microscopio elettronico di semplice uso fu costruito nel 1938 presso l'Università di Toronto dal canadese Eli Franklin Burton (1879-1948) e dai suoi studenti Cecil Hall (1912-1991), James Hillier (1915-2007) e Albert Prebus (1931-1997). La Siemens produsse il primo modello commerciale di microscopio elettronico a trasmissione a partire del 1939. Gli attuali microscopi elettronici arrivano a due milioni di ingrandimenti, eppure rimangono basati sul principio del prototipo di Ruska.
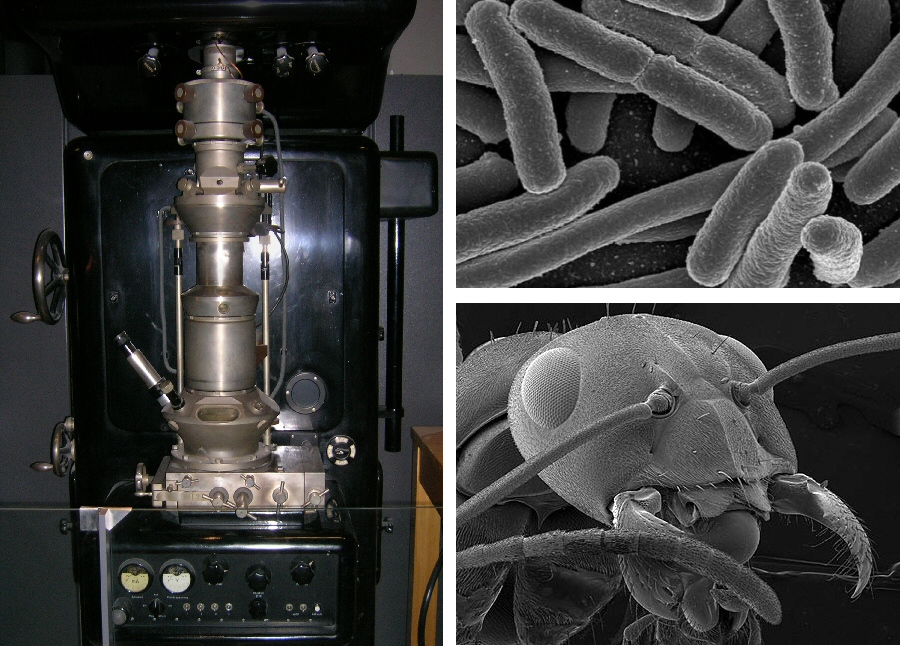
|
A sinistra: modello di microscopio elettronico costruito da Ernst Ruska nel 1933. A destra in alto: batteri di Escherichia coli fotografati dai Rocky Mountain Laboratories. A destra in basso: testa di una formica barbarossa (Formica rufibarbis). |
Fin dalla sua prima apparizione, esso fu vantaggiosamente utilizzato per "vedere" ciò che neppure i microscopi ottici possono arrivare a scoprire, in particolare le microstrutture della materia. A tal proposito, basta ricordare gli enormi progetti raggiunti nelle ricerche sui virus, sul codice genetico, sulle microcricche nei materiali, nella tecnologia della plastica e dei materiali per l'edilizia, e così via.
Il fatto è che, in seguito ai fenomeni di diffrazione, i microscopi ottici hanno una certa capacità di distinguere gli oggetti, detta potere risolutivo, che è misurata dalla distanza dei due oggetti più vicini che si riesce a vedere distinti l'uno dall'altro. Non si può osservare una struttura più piccola della lunghezza d'onda che si usa per illuminarla, e siccome la luce visibile ha una lunghezza d'onda dell'ordine di 1000 Ǻ, cioè di un millesimo di millimetro, non è possibile distinguere tra di loro due punti distanti meno di un millesimo di millimetro l'uno dall'altro. Questi limiti non sono di carattere tecnico, bensì insiti nella natura stessa delle onde elettromagnetiche. Se vogliamo aumentare la risoluzione dei microscopi, dobbiamo adoperare radiazioni di natura diversa, con lunghezza d'onda molto più piccola di quella della luce.
L'idea venuta per primo a Leó Szilárd è quella di adoperare un fascio di elettroni, che come abbiamo visto hanno un'onda associata di de Broglie. Tale onda infatti ha una lunghezza d'onda dell'ordine di 10 Ǻ, e permetterebbe di aumentare di colpo la risoluzione del microscopio di 100 o 1000 volte. Questo però richiede di realizzare dei dispositivi capaci di focalizzare il fascio elettronico, esattamente come fanno le lenti per la luce visibile. Infatti, a frequenze così alte, gli indici di rifrazione di tutti i materiali sono praticamente uguali ad UNO. Per focalizzare gli elettroni bisogna tenere conto del fatto che sono carichi, e dunque che sono deviati da campi elettromagnetici: si parla allora di lenti magnetiche. L'energia di ogni elettrone è pari a:
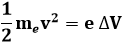
dove ΔV è il potenziale accelerante, per cui la loro lunghezza d'onda di de Broglie è:
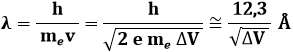
Se ΔV = 9 x 104 V, si ha λ = 0,04 Ǻ. In realtà, purtroppo, le lenti elettromagnetiche producono sempre gravi distorsioni ed aberrazioni, per cui la risoluzione di un microscopio non scende mai sotto alcuni Ǻngstrom. Le possibilità di ottenere una buona immagine con un elevato potere risolutivo dipendono anche, in larga misura, dalle dimensioni trasversali degli oggetti. Mentre nei microscopi ottici gli ingrandimenti massimi sono di circa 20 diametri, con un microscopio elettronico si possono raggiungere anche i 50.000 diametri. L'apparato sperimentale è quello rappresentato qui sotto:
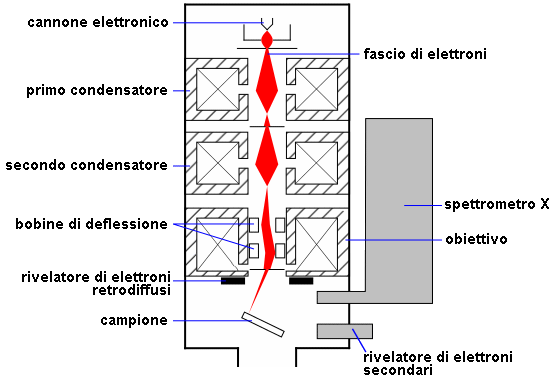
Una sorgente genera elettroni per effetto termoionico, elettroni che vengono subiti accelerati ed inviati sul preparato da osservare mediante una prima lente magnetica detta condensatore. Il fascio elettronico attraversa il campione, originando una prima immagine mediante l'obiettivo; essa viene ulteriormente ingrandita da una terza lente magnetica chiamata proiettivo. L'immagine va a rendere fluorescente un apposito schermo, oppure ad impressionare una lastra fotografica. Naturalmente occorre evitare qualsiasi interazione degli elettroni con molecole che non siano quelle del campione; ci vuole perciò un vuoto molto spinto, inferiore ai 10–4 millimetri di mercurio. Il problema sorge quando si devono introdurre od estrarre i campioni da studiare. Si adopera allora un ingegnoso dispositivo chiamato air lock, rappresentato da un piccolo ambiente del microscopio elettronico che viene automaticamente svuotato dall'aria tutte le volte che, dopo aver introdotto un campione, se ne chiude la porticina!
Faccio notare che il campione deve essere attraversato dagli elettroni, e quindi che esso non può avere uno spessore superiore a 10 o 20 volte la risoluzione massima. Se vogliamo una risoluzione di 10 Ǻ, il preparato non deve essere più spesso di 100 – 200 Ǻ. Ciò implica complesse tecniche di taglio e di fissaggio dei campioni, specialmente se biologici.
Usando nuove e più sofisticate tecnologie, è possibile fare anche di meglio. Il microscopio ionico ad esempio utilizza fasci di ioni invece che di elettroni; ricordando la (4.1), aumentando la massa m delle particelle che illuminano il campione, diventa possibile lavorare con lunghezze d'onda minori, che consentono risoluzioni ancora maggiori, fino ad un Ǻngstrom. Un esempio di microscopio ionico è lo SHIM (Scanning Helium Ion Microscope), che utilizza ioni di elio.
Nel 1937 venne messo a punto il microscopio elettronico a scansione (SEM, "Scanning Electron Microscope"), che genera l'immagine illuminando con un fascio di elettroni un oggetto anche relativamente grande (un insetto, per esempio) e rilevando gli elettroni secondari riflessi, e può quindi fornire immagini tridimensionali; però può analizzare solo oggetti conduttori o semiconduttori. Ne segue che i campioni organici devono essere rivestiti con una sottile lamina metallica, per poter essere osservati. Questo strumento deve operare in condizioni di vuoto molto spinto; una sua evoluzione è il microscopio elettronico ambientale a scansione che non è limitato da questo vincolo, ed è in grado di analizzare campioni di materiale organico modificando a piacimento le condizioni di temperatura, pressione ed umidità. Qui sotto si vede un cristallo di neve ripreso da un microscopio di questo tipo.

Il microscopio elettronico a trasmissione (TEM, "Transmission Electron Microscope") al contrario fa attraversare un campione molto sottile da un fascio di elettroni, quindi con un insieme di magneti ingrandisce l'immagine ottenuta che viene infine proiettata su uno schermo fluorescente, rendendola visibile. Esso fornisce immagini della struttura interna dell'oggetto esaminato, al contrario del SEM che ne mostra solo la superficie, ma permette di ottenere solo immagini bidimensionali. Esso comunque permette di vedere anche le molecole più piccole. Ulteriori perfezionamenti hanno prodotto l'HRTEM ("High-Resolution Transmission Electron Microscope"), con il quale è stato possibile distinguere addirittura i singoli atomi di litio in un composto!
Un altro particolare tipo di microscopio elettronico è quello ad emissione di campo. In esso c'è un bulbo di vetro, all'interno del quale è fatto il vuoto. La superficie del bulbo è ricoperta da una patina fluorescente, mentre al centro è contenuta una punta di tungsteno dal diametro molto piccolo. Tra la punta e la superficie del bulbo è mantenuta una differenza di potenziale molto alta, in modo che nei punti prossimi alla punta esista un campo elettrico molto intenso: si raggiungono valori nell'ordine dei milioni di volt al centimetro. Se la punta è carica negativamente, gli elettroni di essa vengo strappati dal campo elettrico e accelerati radialmente verso lo schermo: dall'immagine ottenuta si può ricostruire la disposizione degli atomi della punta stessa con una risoluzione di circa 25 Å. L'incertezza è dovuta ad effetti quantistici e al moto disordinato degli elettroni. Nel caso in cui, invece, all'interno del bulbo sia iniettato dell'elio e la punta sia caricata positivamente, sono le molecole di gas, ionizzato in prossimità della punta, ad essere accelerate verso le schermo. Siccome questi ioni sono molto più pesanti degli elettroni, la lunghezza d'onda di de Broglie è decisamente ridotta e la risoluzione dello strumento è di circa 1 Ǻ. L'immagine prodotta sullo schermo presenta quindi chiazze scure in prossimità degli interstizi tra due atomi, e tracce dell'arrivo delle molecole di elio ionizzate dai nuclei. Si sono raggiunti ingrandimenti pari a due milioni di diametri!
Il microscopio a scansione per effetto tunnel (STM, "Scanning Tunneling Microscope") invece consente di analizzare la superficie di un campione conduttore o semiconduttore drogato, utilizzando come sensore una punta cresciuta su di un cristallo singolo di tungsteno e rastremata alla sommità fino allo spessore di qualche atomo: a questa punta, posta ad una distanza molto ravvicinata dal campione, viene applicato un piccolo potenziale dell'ordine del Volt rispetto al campione. Quando la punta è sufficientemente vicina al campione, una corrente fluisce dalla punta verso di esso per effetto tunnel elettronico, del quale parleremo più avanti. Poiché la corrente, a parità di tensione applicata, varia con la distanza della punta dalla superficie del campione, tramite un processo di retroazione è possibile mantenere costante tale corrente (o distanza), muovendo la punta sull'asse ortogonale alla superficie del campione con la precisione garantita da un attuatore piezoelettrico. Effettuando una scansione su tutta la superficie del campione e registrando punto per punto i valori della corrente, è possibile ricostruirne un modello tridimensionale. Mediante tale tecnica si riesce a raggiungere precisioni molto elevate, fino a 1 Å! Nel 1989 Donald Eigler (1953-), un ricercatore dell'Almaden Research Center dell'IBM a San Josè, in California, dimostrò che un microscopio STM di bassa temperatura permette di spostare singoli atomi. Il fisico californiano utilizzò 35 atomi di Xenon con i qualì realizzò la scritta IBM:

E non basta. Nel 1993 Eigler insieme a Mike Crommie (1961-) e Christopher Lutz, altri due ricercatori della IBM, realizzò un anello formato da 48 atomi di ferro sopra una superficie di rame. Le increspature all'interno dell'anello sono dovute al comportamento ondulatorio degli elettroni nel sistema:
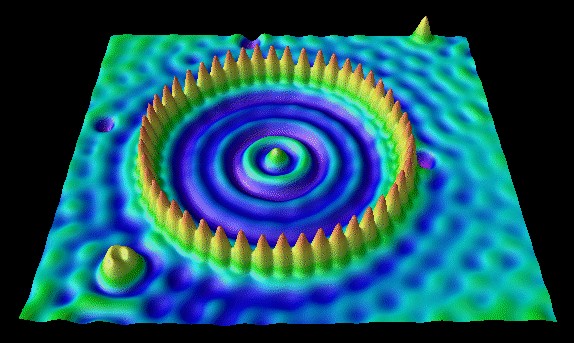
Nel 2012 un gruppo di ricerca dell'Università australiana del New South Wales, coordinato dalla professoressa Michelle Simmons, ha realizzato il transistor più piccolo del mondo, formato da un unico atomo di fosforo fissato su una superficie di silicio. I ricercatori attraverso il microscopio STM hanno individuato un gruppo di sei atomi di silicio e hanno sostituito un atomo di fosforo al posto di uno di questi. La scoperta rivoluzionaria apre le porte ai cosiddetti qubit, bit quantistici in grado di assumere molti più valori rispetto al tradizionale bit del sistema binario. Per la prima volta il gruppo di ricerca è riuscito a controllare un singolo atomo con un livello di accuratezza altissimo.
Chiudiamo con il microscopio a forza atomica (AFM, "Atomic Force Microscope"), inventato da Gerd Binnig (1947-), Calvin Quate (1923-) e Christoph Gerber (1942-) nel 1986. Esso permette di effettuare analisi non distruttive di superfici con una risoluzione inferiore ai 10 Å. Una sonda di dimensioni dell'ordine del micrometro, detto cantilever, esplora la superficie da analizzare a brevissima distanza da essa. Interagendo con gli atomi del campione, per effetto delle forze di Van der Waals, subisce microscopiche deflessioni che, attraverso sensibilissimi dispositivi, vengono tradotte nei dettagli di un'immagine topografica tridimensionale della superficie del campione. Rispetto al SEM e allo STM, il microscopio a forza atomica ha il vantaggio di consentire analisi non distruttive su campioni non trattati e di adattarsi anche a campioni di materiale non conduttore, fornendone una reale mappa tridimensionale, ma ha il difetto di una profondità di scansione limitata e di un tempo necessario all'indagine relativamente lungo. Tipicamente viene impiegato per esaminare macromolecole biologiche, parti di microrganismi e dispositivi a semiconduttore. Qui sotto vedete un'immagine di un cristallo di grafite ottenuta con questo tipo di microscopio: è ben visibile la disposizione degli atomi di carbonio in un reticolo esagonale.

.
4.5 I raggi misteriosi
Se, come ha scritto il grande fisico e divulgatore George Gamow (1904-1968), i primi trent'anni del Ventesimo Secolo vanno considerati « i trent'anni che sconvolsero la Fisica » (titolo di un suo celeberrimo saggio del 1966), è però vero che non ci sarebbe stato nessuno sconvolgimento se l'ultimo decennio del secolo precedente non avesse visto la scoperta delle onde hertziane e dell'effetto fotoelettrico ad opera di Heinrich Hertz (1857-1894), dell'elettrone ad opera di Joseph John Thomson (1856-1940), della radioattività ad opera di Henri Becquerel (1852-1908), Pierre Curie (1859-1906) e Marie Curie (1867-1934), e soprattutto dei raggi X.
Questa scoperta fu ottenuta casualmente nel 1895 dal tedesco Wilhelm Conrad Röntgen (1845-1923). Anche se nella storia della Fisica Moderna la figura dello "scienziato solitario" stile Röntgen è ormai sparita, come dimostrano i Premi Nobel assegnati solo ad equipe di Fisici, tuttavia le grandi scoperte nascono ancora da qualche evento insolito notato da uno sperimentatore magari fino ad allora sconosciuto. Lo dimostra lo straordinario risultato ottenuto per caso la notte del 20 settembre 2016 da Victor Buso, fabbro argentino di 58 anni con la passione per l'astronomia, che mentre riprendeva alcune fotografie astronomiche con la nuova telecamera installata sul suo telescopio, si è accorto di una nuova stella apparsa nella galassia NGC613 nella costellazione dello Scultore, a circa 80 milioni di anni luce da noi. Si trattava di una supernova nelle prime fasi della sua esplosione, un evento così raro da osservare che la scoperta di Buso è stata paragonata alla « vittoria in una lotteria cosmica »!

|
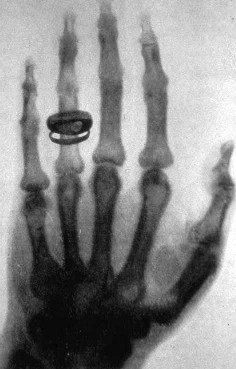
A sinistra: Wilhelm Conrad Röntgen (Lennep, 27 marzo 1845 – Monaco di Baviera, 10 febbraio 1923). A destra: foto della mano sinistra della moglie di Albert von Kölliker scattata da Röntgen il 23 gennaio 1896 |
I raggi X rappresentano proprio l'esempio di un evento casuale e fortunato che capita in concomitanza con il fiuto di un grande fisico sperimentale. Infatti nel 1890 un certo F. Smith stava eseguendo degli esperimenti con i tubi di Crookes, quando notò che delle pellicole fotografiche, conservate in un cassetto sotto accurata protezione contro la luce, erano rimaste impressionate; tuttavia egli si limitò ad arrabbiarsi con il proprio assistente, rimproverandolo per la scarsa cura con cui le aveva trattate, e così mancò la scoperta del secolo. Invece, nel 1895 Röntgen ebbe la fortuna di notare che, mentre era in funzione il tubo di Crookes con cui lavorava, una lastra di platinocianuro di bario posta sul tavolo di lavoro emetteva un'intensa fluorescenza. Poiché essa si verificava anche schermando il tubo con fogli di carta nera, lo scienziato si rese conto che il suo dispositivo doveva emettere delle radiazioni assai più penetranti della luce visibile. Anzi, proprio mentre spostava la lastra, notò con sorpresa su di essa l'ombra delle ossa della propria mano. Insomma, mentre alla luce il nostro corpo è opaco, questi raggi parevano in grado di attraversare i tessuti ossei come se fossero vetro. Dopo essere rimasto chiuso per un mese nel suo laboratorio a studiare i nuovi raggi, il 28 dicembre 1895 egli comunicò le sue scoperte all'Accademia di Medicina dell'Università di Würzburg, annunciando per la prima volta di aver trovato il modo per "scrutare" all'interno del corpo umano, senza bisogno di tagliarlo. Subito i suoi risultati suscitarono grande impressione, furono ripetuti in ogni laboratorio in Europa e in America, e a Vienna si cominciò subito ad eseguire le prime radiografie. Non sapendo spiegare la natura di tali raggi, Röntgen li chiamò con il nome dell'incognita matematica, cioè X. Ben presto però si scoprì che non poteva trattarsi di corpuscoli, un po' perchè erano troppo penetranti senza per questo essere distruttivi come proiettili di cannone, ed un po' perchè i campi elettrici e magnetici non riuscivano a deviarli. Tuttavia, tutte le esperienze di diffrazione tentate da Röntgen fallirono, per cui non si riusciva a metterne in evidenza neppure delle proprietà ondulatorie: il mistero legato al loro nome sembrava infittirsi, anziché dileguarsi. A ciò si aggiunge il fatto che, nel 1903, il fisico francese Renè Blondlot (1849-1930) asserì di aver scoperto altri misteriosi raggi da lui battezzati raggi N (dal nome della sua città, Nancy), dotati di proprietà quasi metafisiche: sarebbero stati in grado di aumentare la luminosità di una scintilla, di acuire la capacità visiva degli esseri umani e di eseguire uno screening dell'interno del corpo umano.
A poco a poco però il mistero circa gli enigmatici raggi scoperti a cavallo fra Otto e Novecento cominciò a dissiparsi. Lo spettroscopista americano Robert Williams Wood (1868-1955), scettico circa le inverosimili proprietà attribuite ai raggi N, nel settembre 1904 si recò a Nancy di persona, nel laboratorio di Blondlot, e dimostrò in via definitiva che i raggi N non esistono, ma erano dovuti all'autoconvincimento da parte di un gruppo di scienziati francesi animati da sentimenti patriottici di aver compiuto una scoperta ancor più epocale di quella del tedesco Röntgen. Non a caso, per descrivere questo fenomeno è stato coniato il concetto di « scienza patologica »: chi vuole saperne di più, consulti questo capitolo di un altro mio ipertesto. Quanto ai raggi X, che invece sicuramente esistevano, fondamentale fu il contributo del tedesco Max Von Laue (1879-1960), che nel 1914 riuscì a far diffrangere i raggi X attraverso un reticolo cristallino di nichel. Ciò significava che la lunghezza d'onda dei raggi X ha lo stesso ordine di grandezza dei passi reticolari. Fu il fisico australiano Sir William Lawrence Bragg (1890-1971) ad avere l'idea di sfruttaretale diffrazione per determinare la struttura microscopica di cristalli e molecole. Nel 1953 James Watson (1928-) e Francis Crick (1916-2004) sfruttarono i lavori della sfortunata Rosalind Franklin (1920-1958) per annunciare al mondo che la molecola di DNA ha la forma di una doppia elica, come scoperto dalla Franklin proprio attraverso la diffrazione di raggi X; Crick e Watson ottennero il Premio Nobel, mentre il contributo di Rosalind Franklin, che morì a soli 37 anni per un cancro alle ovaie, fu quasi completamente dimenticato, come spesso accaduto alle donne nella storia della Scienza.
|
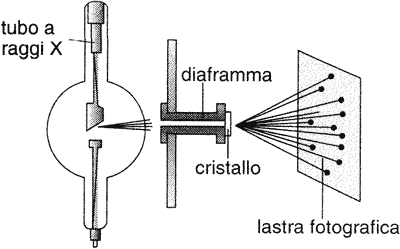
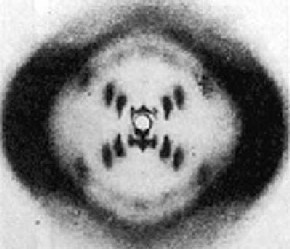
A sinistra: tubo a raggi X per esperimenti di diffrazione. A destra: la famosissima "foto 51" scattata da Rosalind Franklin nel maggio 1952 che ha permesso di dedurre la struttura a doppia elica del DNA |
Tutto ciò implica che i raggi X siano in realtà radiazioni elettromagnetiche ad altissima frequenza. Se infatti la lunghezza d'onda è dell'ordine dell'Ǻngstrom, vuol dire che la frequenza è compresa tra 3 ∙ 1016 e 3 ∙ 1018 Hertz, contro i 4 ∙ 1014 – 7 ∙ 1014 Hz della luce visibile. Per forza non diffrangevano attraverso le fenditure attraverso cui diffrange la luce! Ma come si possono generare radiazioni con frequenza tanto alta? Lo spettro dei raggi X è formato, come si vede qui sotto, da un fondo continuo ad alta frequenza e da alcune righe sovrapposte, dipendenti dalla natura dell'anticatodo del tubo di Crookes, dette radiazione X caratteristica. Lo spettro continuo si origina a causa di una perturbazione indotta negli elettroni emessi dal catodo, allorché sbattono ad alta energia contro l'anticatodo. Il brusco frenamento, in tedesco "bremsstrahlung", fa sì che essi irraggino quasi tutta la loro energia sotto forma di quanti di radiazione ad altissima frequenza. Sappiamo infatti che le cariche accelerate irraggiano, e ciò vale anche per quelle decelerate: tanto più è brusco il frenamento, tanto è maggiore l'irraggiamento. Si parla perciò di radiazione di bremsstrahlung. L'energia cinetica degli elettroni incidenti è pari a quella comunicata loro dal campo elettrico accelerante, cioè e V. Avremo dunque:
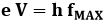
da cui:
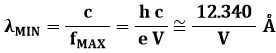
Così, se uso un potenziale accelerante di 25 kV, ho una lunghezza d'onda di circa 0,5 Ǻ, dell'ordine appunto del passo reticolare dei cristalli. Osserviamo che la produzione di raggi X può essere considerata una specie di effetto fotoelettrico inverso: là l'energia del fotone era comunicata all'elettrone, qui avviene l'esatto contrario. Come nell'effetto fotoelettrico non si ha emissione di elettroni finchè l'energia h f dell'onda non supera un valore di soglia h f0, così nel nostro caso non si ha l'emissione di raggi X finché la tensione acceleratrice non raggiunge un valore tale da conferire agli elettroni primari l'energia sufficiente per interessare nel processo d'urto gli strati interni dell'atomo.
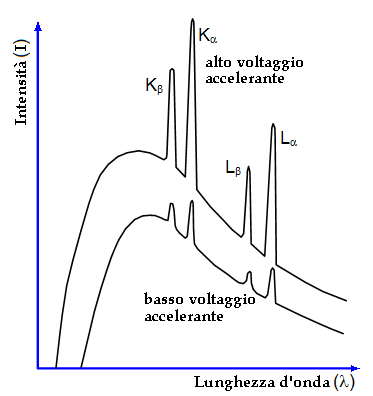
Con l'aumentare della tensione V compare, sovrapposto allo spettro continuo, una serie di righe spettrali, che dipendono dal materiale di cui è composto l'anticatodo. Ciò si spiega ammettendo che gli elettroni primari, quando hanno raggiunto una sufficiente energia, espellono dall'anticatodo alcuni elettroni delle orbite più interne. Essi o vanno a finire su livelli non occupati, o sono catapultati fuori dall'atomo. L'elettrone secondario lascia un posto vacante, che può essere occupato dall'elettrone di un'orbita più esterna, originando la cosiddetta serie K. Analogamente si formano le serie L, M, N come nella formula di Balmer. Nel 1913 il fisico britannico Henry Moseley (1887-1915), che purtroppo il 10 agosto 1915 morì nella tragica Battaglia di Gallipoli durante la Grande Guerra, formulò una legge empirica, oggi nota col nome di legge di Moseley, la quale esprime la dipendenza della frequenza f dei raggi X caratteristici emessi da un elemento chimico in funzione del relativo numero atomico Z:
![]()
dove A e B sono due costanti, tipiche rispettivamente dell'elemento considerato e della serie spettrale considerata. Oggi sappiamo che tale legge può essere ricavata per via teorica dal modello atomico di Bohr. Ad esempio, nel caso della riga Kα (transizione dal livello 2p a 1s) originata da un atomo idrogenoide, cioè con un elettrone solo, la precedente si scrive:
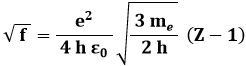
Ed allora in questo caso particolare la costante A vale 4,98 ∙ 107 (Hz)1/2. Se l'anticatodo è di alluminio (Z = 13), la frequenza della riga Kα è pari a 2,98 ∙ 1016 Hz, ricadendo proprio nella regione dei raggi X.
.
E ora, possiamo porre le basi della nuova meccanica, la Meccanica Quantistica: lo faremo nel capitolo successivo. Per tornare all'indice, invece, cliccate qui.
