I metalli e il gas di elettroni

.

8.1  La molecola risonante

Il discorso sui legami chimici non è ancora terminato; anzi, si può dire che la parte più importante cominci ora. Siamo però costretti a prenderla alla larga, cominciando con una molecola che apparentemente non c'entra nulla con il discorso che vogliamo portare avanti in questo capitolo: quella del benzene (C₆H₆), un idrocarburo aromatico incolore altamente infiammabile, dall'odore caratteristico, scoperto nel 1825 dal grande Michael Faraday, che lo isolò dal petrolio. Oggi sappiamo che purtroppo ha effetti terribilmente cancerogeni.

Come costruire la sua molecola? Le verifiche sperimentali hanno dimostrato che i sei atomi di carbonio del benzene sono disposti ai vertici di un esagono regolare. Ricordando che il carbonio ha valenza quattro dopo che i quattro elettroni 2s e 2p si sono disposti tutti con gli spin paralleli, posso pensare che ciascun atomo di carbonio abbia i suoi orbitali più esterni ibridizzati di tipo sp²; in altre parole, l'orbitale 2s e due orbitali 2p danno vita a tre orbitali lobati separati di 120° l'uno dall'altro, mentre il terzo orbitale 2p resta ortogonale al loro piano. Se disponiamo gli atomi di carbonio e di idrogeno come in figura sottostante, la forma della molecola di benzene sembra perfettamente spiegata.

_____

Tuttavia, come si legano tra di loro gli orbitali 2p rimanenti e non ibridizzati? Come si vede, essi possono dare vita ad orbitali di tipo π in due modi possibili, alternati l'uno con l'altro. Entrambe le strutture proposte, però, sono in contrasto con l'esperienza. Infatti gli atomi di carbonio legati con doppio legame sono più vicini tra di loro di quelli legati con legame semplice, come si può dimostrare, e quindi l'esagono dovrebbe essere irregolare, come si vede qui sopra a destra. Per superare la contraddizione tra le strutture irregolari previste e quella regolare osservata, nel 1865 il chimico tedesco Friedrich August Kekulé von Stradonitz (1829-1896) propose che i legami di tipo π ortogonali al piano della molecola si rompano in continuazione, ricostituendosi immediatamente dalla parte opposta. Praticamente, se indichiamo i sei atomi di carbonio con i numeri 1, 2, 3, 4, 5 e 6, ad un dato istante si formeranno i legami 1–2, 3–4 e 5–6; all'istante successivo, rotti questi, si formeranno i legami 2–3, 4–5 e 6–1; successivamente si riformeranno i legami precedenti; e così via. In questo modo, in media l'esagono assumerebbe una forma regolare, perchè i legami doppi e semplici si alternerebbero di continuo con ritmo periodico nel tempo.

Tale stravagante teoria prevede comunque, per la molecola di benzene, una simmetria per rotazione di 120°; invece, l'osservazione sperimentale mostra che la molecola incriminata ha una simmetria per rotazione di 60°. In altre parole, non c'è posto per il legame π. Per almeno cinquant'anni questo fatto costituì un inestricabile mistero. Ma, come si sa, il progresso scientifico è costituito proprio dalla successiva soluzione di misteri apparentemente insolubili. In questo caso, la risposta fu data proprio dalla Meccanica Quantistica. Già nel 1926 Wernher Heisenberg, una nostra vecchia conoscenza, avanzò l'ipotesi che la reale configurazione elettronica del benzolo fosse una combinazione lineare delle due proposte da Kekulé, e diede a questo fenomeno il nome di risonanza.

Ben presto si scoprì che questo fatto è generale. In molti casi, quando una molecola può essere descritta da più configurazioni differenti, quella reale è risonante tra tutte queste, cioè risulta da una loro combinazione lineare. Il caso più semplice è quello rappresentato dalla molecola di anidride carbonica (CO₂). Il modo più comune per descriverla consiste nel supporre un'ibridizzazione di tipo sp, che dà alla molecola una forma lineare come quella dell'acetilene vista nel § 7.7, ma che lascia liberi due orbitali 2p, i quali danno vita a due legami di tipo π, ortogonalmente all'asse della molecola. Il legame tra C ed O è dunque doppio:

Sperimentalmente, però, la distanza media tra O e C misura 1,16 Å, ed è un po' più piccola del valore calcolato per il legame doppio C = O, che dovrebbe essere pari a 1,22 Å, ma un po' maggiore di quello calcolato per il legame triplo C ≡ O, paria 1,12 Å. Dunque, in realtà, il legame non sembra né doppio né triplo. La soluzione la si trova osservando che la molecola di CO₂ si può costruire anche supponendo che il carbonio formi due legami con uno dei due ossigeni tramite orbitali molecolari, e prenda pure uno dei suoi lone pair (§ 7.8), mentre ne cede uno egli stesso all'altro ossigeno, come schematizzato nella figura sottostante:

Naturalmente, i due atomi di ossigeno sono identici tra di loro, quindi posso avere anche la configurazione simmetrica:

(abbiamo indicato i lone pairs non coinvolti nel legame). Queste due ulteriori configurazioni sono polari, mentre la configurazione O = C = O è non polare. Appare perciò logico che la reale configurazione della CO₂ sia una combinazione lineare delle tre sopra proposte, come avviene regolarmente nella Meccanica Quantistica. Si ottiene così una previsione per il valore della distanza  assai prossima a quello ottenuto sperimentalmente.

Naturalmente il legame reale all'interno della CO₂ non è nessuno dei tre sopra proposti, ma presenta contemporaneamente le proprietà di tutti e tre; per usare un interessante paragone coniato dal chimico americano George Willard Wheland (1907-1962), il mulo presenta contemporaneamente alcune caratteristiche dell'asino e alcune del cavallo, ma non è vero che in lui vi è una parte di solo asino e una di solo cavallo, né egli è per un certo tempo solo asino e per un certo tempo solo cavallo. Per questo, si può affermare che il mulo è una forma di risonanza fra l'asino e il cavallo. La stessa cosa capita al benzene, che risuona tra le due strutture rappresentate qui sopra e anche fra altre, il cui peso nella combinazione lineare è però trascurabile. Ma com'è che appare realmente la distribuzione di densità elettronica ortogonalmente al piano della molecola? Per arrivarci, il modo più semplice è l'applicazione del vecchio metodo della combinazione lineare degli orbitali atomici (LCAO), vista nel § 7.4. Noi sappiamo che la prima situazione comporta un legame tra gli orbitali degli atomi di carbonio 1 e 2, uno tra quelli 3 e 4, uno tra quelli 5 e 6. Determinare l'orbitale molecolare significa combinare linearmente gli orbitali 2p_z di questi atomi, supponendo l'asse z normale al piano molecolare. Nel secondo caso, invece, dovremo combinare linearmente gli orbitali degli atomi 2 e 3, 4 e 5, 1 e 6.

Il risultato di una combinazione lineare tra queste due situazioni è, come si intuisce, una combinazione lineare con pesi opportuni di tutti gli orbitali 2p_z dei sei atomi di carbonio. Detti c_j questi pesi, con j = 1, 2, ..., 6, si potrà scrivere la funzione d'onda risultante nella forma:

          (8.1)

Occorre calcolare i coefficienti . Allo scopo, ricordiamoci che le osservazioni sperimentali indicano per la molecola di  una simmetria per una rotazione di 60°. Se cioè ruotiamo la molecola di 60° attorno al suo centro, troveremo che la funzione d'onda rimane inalterata. Ora, si può dimostrare che l'operatore "rotazione di 60° attorno al centro della molecola è rappresentato dal fattore moltiplicativo:

con n = 0, 1, 2, ..., 5. Indicando la funzione d'onda ruotata di π/6 con la scrittura Ψ_60°, si ha:

   Ψ_60° = Ψ e^{2 i n π/6}          (8.2)

Ma, se la molecola è ruotata di 60°, l'atomo 2 prende il posto di 1, il 3 di 2, e così via, in modo che le funzioni d'onda debbano trasformarsi le une nelle altre nel modo che segue:

( 2p_z )₁ → ( 2p_z )₂

( 2p_z )₂ → ( 2p_z )₃

_.........

( 2p_z )₆ → ( 2p_z )₆

E quindi, per la (8.1) e la (8.2):

c₁ ( 2p_z )₁ + c₂ ( 2p_z )₂ + ... + c₆ ( 2p_z )₆ =

= e^{2 i n π/6} { c₆ ( 2p_z )₆ + c₁ ( 2p_z )₁ + ... + c₅ ( 2p_z )₅ }

Ma le funzioni d'onda (2p_z)_j sono linearmente indipendenti tra loro, dunque questa è valida solo se:

c₁ = c₂ e^{2 i n π/6}

c₂ = c₃ e^{2 i n π/6}

_.........

c₆ = c₁ e^{2 i n π/6}

Sostituendole l'una nell'altra si trova:

c₆ = e^{2 i n • 6 π/6}

E, risolvendo più in generale:

c_j = e^{2 i n j π/6}          (8.3)

Con questa espressione, i coefficienti della (8.1) sono determinati a meno di un coefficiente di normalizzazione:

Il risultato è piuttosto sorprendente. Se infatti costruiamo esplicitamente la funzione d'onda, ci accorgiamo che essa ingloba tutti e sei i nuclei di carbonio del benzene! L'orbitale infatti è costituito da due nubi di carica negativa, come si vede in figura sottostante, una al di sopra e una al di sotto del piano della molecola, entrambe a forma di anello:

Gli orbitali 2p_z che occupano questo orbitale benzenico possono perciò scorrere lungo tutta la molecola! Del resto, i fattori c_j ora calcolati non rappresentano altro che dei fattori di fase, i quali indicano che l'orbitale ha l'aspetto di un'onda stazionaria lungo il perimetro dell'esagono del benzene. La cosa è estremamente importante, perché significa che gli elettroni 2p_z del benzene non sono localizzati su di un preciso atomo di carbonio o su una precisa coppia di essi, come imporrebbe la logica del legame covalente. Si parla perciò di elettroni delocalizzati, e questo particolare tipo di legame è detto legame delocalizzato.

In realtà non si tratta di un nuovo tipo di legame, bensì di una conseguenza diretta dell'applicazione dei principi della Meccanica Quantistica al legame covalente. Tuttavia, la tentazione di trattarla come una nuova realtà fisica è forte, così come i paleontologi, appena recuperano un nuovo ossicino, in genere sono rapidi nell'attribuirlo a una nuova specie, cui magari assegnare il proprio nome. Comunque sia, questo tipo di legame merita almeno un simbolo tutto suo: per indicarlo, nella formula di struttura della molecola si introduce un ovale all'interno dell'esagono, come si vede qui sotto. Per la prima volta infatti scopriamo di avere a che fare con un orbitale che ingloba più di due atomi, e almeno di questa novità dobbiamo dargli atto!

.

8.2  Banda di valenza e banda di conduzione

Naturalmente i miei lettori più attenti avranno colto una contraddizione in quanto si è detto finora. Gli elettroni 2p_z sono sei, tanti quanti gli atomi di carbonio, mentre noi abbiamo parlato di un solo orbitale: è ovvio che esso non può accogliere tutti e sei gli elettroni, per via del Principio di Esclusione di Pauli, che continua a valere anche per i legami più strambi che ci vengono in mente, giacché continuano a valere i postulati della Meccanica Quantistica, cioè quelle "Tavole della Legge" con cui tutta la Fisica Atomica e Molecolare può essere costruita. Allora noi dobbiamo per forza avere a che fare almeno con tre orbitali. Se però ricordiamo i risultati ottenuti per il legame ione-idrogeno e per il legame idrogeno, con due nuclei (e quindi due orbitali atomici di partenza) si arrivava a due orbitali molecolari: uno legante ed uno antilegante. Sembra naturale che anche nel benzene debba accadere la stessa cosa; infatti il numero j presente nella (8.3) si può interpretare come un numero quantico che etichetta le soluzioni dell'Equazione di Schrödinger della molecola di benzene. Poiché j va da 0 a 5, avremo sei soluzioni, e quindi sei orbitali, di cui tre leganti e tre antileganti. In corrispondenza di essi avrò anche sei valori di energia.

Essi sono piuttosto complicati da scrivere; il loro significato è però intuibile facendo ricorso alla seguente semplificazione. Siccome la molecola di benzene è simmetrica per rotazioni di 60°, come si vede qui sopra, possiamo attribuire a j i valori:

j = – 2, – 1, 0, + 1, + 2, + 3

senza mutare sensibilmente il risultato. È come ruotare una stella di Davide di un qualunque multiplo di 60°: nessuno si accorgerà del cambiamento. Allora, sviluppando i calcoli, possiamo attribuire all'energia il valore:

E = E₀ + 2 K cos (k x)

dove E₀ è una quantità indipendente da j, K è l'integrale di scambio per la molecola di benzene, definito in modo del tutto analogo a quello della molecola di idrogeno (vedi § 7.4). Invece k è un vettore d'onda che vale:

essendo a il passo della molecola di benzene, ovvero la rotazione effettiva che un atomo di carboni deve compiere per sovrapporsi a quello adiacente. Allora:

• se j = 0, k = 0 e si ha E₀ + 2 K

• se j = ± 1, k =  ± a π / 3 e si ha E₀ + K

• se j = ± 2, k =  ± 2 a π / 3 e si ha E₀ – K

• se j = 3, k = a π e si ha E₀ – 2 K

Possiamo perciò rappresentare i livelli energetici nel diagramma ciclico della figura sottostante. I livelli energetici corrispondenti a j = ± 1 e a j = ± 2 sono degeneri, cioè hanno la stessa energia. Non ci si lasci ingannare dai segni: K è negativo, dunque il livello energetico più baso è E₀ + 2 K, il più alto è E₀ – 2 K.

Il livello con j = 0 è perciò detto livello energetico fondamentale o "ground zero", e ad esso (k = 0) corrisponde effettivamente l'orbitale anulare sopra descritto. Gli altri invece sono livelli eccitati. Il livello con j = ± 1 è costituito da due orbitali degeneri che corrispondono a due anelli spezzati, come si vede a sinistra; essi sono dunque localizzati. Questi tre orbitali sono leganti, come si dimostra graficandone l'energia in funzione della coordinata curvilinea che percorre l'intero esagono del benzene, e se ci troviamo a temperature basse (in pratica, anche a temperatura ambiente), tali orbitali "drenano" tutti e sei gli elettroni 2p_z a spasso nel benzene. Sono perciò detti anche orbitali di valenza.

Come si vede, gli orbitali localizzati (che presentano nodi al centro dei lati opposti dell'esagono) per j = ± 1 sono separati dallo stato fondamentale da un salto energetico pari a | K |. Invece, ad una distanza | 2 K | dai livelli con j = ± 1 si trovano quelli con j = ± 2 che sono antileganti, e differiscono a loro volta di un salto energetico | K | dallo stato più eccitato. Il diagramma ciclico sopra proposto, dunque, assomiglia effettivamente ad una stella di Davide, per cui il paragone fatto poco fa era tutt'altro che fuori luogo! Ma, in virtù di questa somiglianza, i tre orbitali leganti sono nettamente separati dai tre antileganti da un salto energetico o gap. Si dice perciò che costituiscono due bande di orbitali. Gli orbitali di valenza danno luogo alla cosiddetta banda di valenza; gli elettroni in essa contenuti sono in parte localizzati e in parte delocalizzati, ma sono comunque occupati a riempire orbitali, se riescono a saltare nella loro banda superiore; non per questo distruggono le molecole perchè, come si ricorderà, basta avere più elettroni negli orbitali leganti che in quelli antileganti. Però sono liberi di muoversi lungo l'anello benzenico, e sono responsabili della conducibilità elettrica da parte della microspira costituita dai sei atomi di carbonio del benzene. Ciò si manifesta nello spiccato diamagnetismo presentato dalla molecola, la quale subisce un forte momento magnetico indotto, assai superiore a quello che si avrebbe se gli orbitali 2p_z degli atomi di carbonio non si mischiassero tra loro. Per questo si dice che gli orbitali antileganti di energia superiore costituiscono la cosiddetta banda di conduzione.

Riprendiamo ora in mano il concetto di elettronegatività, già spiegato nel § 7.7. Se ricordate, l'idrogeno possiede un valor medio di elettronegatività, posto convenzionalmente pari ad x_H = 2,1 per non aver a che fare con valori negativi di elettronegatività. Come si vede nella tabella sottostante, alcuni elementi hanno elettronegatività superiore, altri inferiore a quella dell'idrogeno:

Gli elementi elettronegativi nella colonna di sinistra si dicono non metalli, quelli elettropositivi nella colonna di destra sono i metalli. Come già sappiamo, le elettronegatività maggiori sono concentrate nella sezione in alto a sinistra della tavola periodica; qui dunque sono radunati i non metalli. I metalli occupano la maggio parte della tabella, e quelli contenuti nei gruppi I B – VIII B sono detti metalli di transizione. Gli elementi che si trovano adiacenti alla frontiera tra metalli e non metalli si dicono anfoteri, perchè presentano sia caratteristiche metalliche che non metalliche. I metalli hanno le seguenti caratteristiche:

• sono duttili e nalleabili, cioè lavorabili; in altre parole, mediante azioni meccaniche è possibile ridurli a fili o a lamine sottili.

• hanno ottima conducibilità elettrica e termica.

• presentano alti punti di fusione e di ebollizione.

• possiedono la caratteristica lucentezza metallica.

Esiste una teoria del legame chimico in grado di spiegare la costituzione elementare dei metalli e le loro proprietà ora elencate? In quel che segue cercheremo di rispondere a questa domanda. Le prime ricerche in tal senso misero in evidenza che i metalli hanno una struttura molto simile a quella del diamante e del cloruro di sodio, cioè la disposizione dei loro atomi è quella ordinata e regolare di un cristallo. Tuttavia, i bassi valori di elettronegatività degli atomi dei metalli esclusero che essi potessero dare vita a legami ionici (se non con atomi non metallici, come avviene appunto nel cloruro di sodio), mentre i bassi valori di energia di ionizzazione e di affinità elettronica indicavano che i metalli hanno ben poca tendenza a formare tra di loro dei legami covalenti: solo nei vapori metallici, a temperature altissime, è possibile rintracciare molecole biatomiche di metalli (Li₂, Na₂), ben poco stabili però, visto il modesto valore dell'energia di legame in gioco. Inoltre, siccome il metallo risulta dotato di ottime proprietà meccaniche, è impensabile che la formazione di solidi metallici sia da attribuire a legami di Van der Waals.

Ne segue che, per spiegare le caratteristiche dei metalli, bisogna ipotizzare l'esistenza di un legame del tutto nuovo, detto per l'appunto legame metallico. La prima ipotesi avanzata per spiegare le proprietà metalliche è quella del tedesco Paul Drude (1863-1906), avanzata nel 1900, secondo la quale, vista la bassa elettronegatività e il basso potenziale di ionizzazione degli atomi metallici, è facile che essi perdano gli elettroni periferici. Questi ultimi allora costituirebbero un gas di elettroni che, insinuandosi tra tutti gli ioni metallici, li terrebbe insieme come una specie di cemento che, impastato con la ghiaia, ne tiene insieme i singoli componenti in una struttura stabile:

In pratica, il modello di Drude è molto simile a quello del cristallo ionico: anche qui si alternano cariche positive (gli ioni metallici) e negative (gli elettroni, rappresentati qui sopra tramite puntini azzurri), Gli elettroni "gasificati" attrarrebbero tra di loro gli ioni e ne schermerebbero le cariche positive, impedendo che si respingano.

Questo modello è ovviamente ingenuo, ma non è troppo lontano dalla realtà. Se infatti ricordiamo quanto abbiamo detto a proposito del legame ione-idrogeno, scopriamo che gli orbitali leganti sono quelli in cui l'elettrone si trova, mediamente, nella regione di spazio fra i due nuclei, in modo da schermare le loro cariche positive e da attirarli entrambi. La stessa cosa si produce per i solidi; anzi, è interessante osservare l'analogia fra quella semplice struttura e quella, più complicata perchè formata da un numero di Avogadro di nuclei, del solido metallico. Consideriamo, per esempio, due nuclei di atomi metallici come quelli di litio. Esso è monovalente, perchè ha due elettroni nell'orbitale 1s e uno dell'orbitale 2s; i primi due restano nella loro shell interna, il terzo può servire per il legame. Con due atomi ho due elettroni disponibili per il legame, esattamente come nella molecola di idrogeno. Siccome, mischiando i loro orbitali 2s, ottengo un orbitale molecolare legante e uno antilegante, è ovvio che entrambi gli elettroni finiranno nel primo di essi, lasciando vuoto l'orbitale antilegante.

Se invece considero tre atomi di litio, essi legandosi daranno vita a tre orbitali, che potranno ospitare in tutto sei elettroni; siccome di elettroni di valenza ne ho tre, due di essi si sistemeranno nell'orbitale inferiore, uno in quello intermedio e nessuno in quello superiore. Con quattro atomi di litio si formeranno quattro orbitali, di cui i primi due saranno completamente occupati dai quattro elettroni messi in comune; e così via, come si vede in figura qui a destra.

Se io utilizzo un numero N molto grande di atomi di litio, allora è ragionevole pensare che otterrò N orbitali, di cui N / 2 leganti ed N / 2 antileganti. Gli N elettroni di valenza saranno tutti dislocati, a temperature basse, negli N / 2 orbitali di energia inferiore. Questa situazione ci ricorda molto da vicino quella della molecola di benzene, dove i sei atomi di carbonio con sei elettroni danno vita a sei orbitali, di cui tre leganti e tre antileganti. Questi orbitali si estendono su tutto l'esagono della molecola, dunque i sei elettroni sono delocalizzati lungo tale esagono. Allo stesso modo, se risolviamo l'equazione di Schrödinger corrispondente, è abbastanza logico trovare che anche gli N elettroni del metallo sono delocalizzati sui suoi N atomi! Gli orbitali metallici insomma si estendono all'intero solido metallico, che può avere dimensioni macroscopiche, e gli elettroni sono messi in comune tra tutti i possibili atomi che lo costituiscono! In pratica il legame metallico può essere classicamente immaginato come un reticolo cristallino formato dai cationi dei metalli e da un "gas" di elettroni delocalizzati, in cui la delocalizzazione elettronica è spinta al massimo grado. La molecola di benzene si comporta come un pezzetto di metallo in miniatura, e a noi è stata utilissima per capire come vanno le cose in un sistema talmente più complicato, eppure talmente simile, da consentirci l'applicazione del metodo deduttivo!

La teoria rigorosa del legame metallico la dobbiamo a Enrico Fermi (1901-1955) e Paul Dirac (1902-1984), e non è altro che un perfezionamento del modello di Drude, tenendo conto dei risultati della Meccanica Quantistica. Infatti anche in questo modello più perfezionato gli elettroni non rappresentano altro che una sorta di "gas" addensato negli orbitali leganti del metallo, detto in gergo "gas di elettroni di Fermi"; in analogia a quanto visto per la molecola di benzene, questi orbitali costituiscono la cosiddetta banda di valenza, mentre gli orbitali antileganti costituiscono la cosiddetta banda di conduzione. Il concetto di "banda" come gruppo di orbitali lo dobbiamo al fisico svizzero Felix Bloch (1905-1983). L'evidenza di queste bande di energia nel legame metallico può essere messa in evidenza spettroscopicamente: se un metallo viene bombardato con elettroni fortemente accelerati, anche alcuni degli elettroni di più bassa energia presenti nel cristallo possono essere proiettati fuori. Il "buco" lasciato libero da questo elettrone viene allora occupato da un altro elettrone presente sul livello energetico successivo a contenuto di energia maggiore, e così via. A ciascuno di questi salti elettronici in serie corrisponde l'emissione di una radiazione, la cui frequenza (E = h f) ci dà una misura del salto energetico. Si ottiene così uno spettro di banda che ripete la banda di energia su cui sono distribuiti gli elettroni di valenza nel metallo.

In questo modo si spiegano le peculiarità dei metalli: la conduzione del calore e la loro lucentezza sono legate alla mobilità degli elettroni di valenza delocalizzati, che incrementano la loro energia cinetica, mentre duttilità e malleabilità sono spiegabili mediante il libero scorrimento reciproco dei piani reticolari, per via dei legami non direzionati, il quale non provoca la distruzione del cristallo in quanto il legame non è costituito da pochi elettroni localizzati, ma da tutti gli elettroni disponibili. La presenza di legami molti forti all'interno del legame metallico spiega anche altre caratteristiche proprie dei metalli stessi come l'alta densità, la non solubilità e i punti di ebollizione e fusione molto alti.

Nei metalli, che come detto costituiscono i tre quarti degli elementi chimici, le due bande di valenza e di conduzione sono pressoché sovrapposte, o sono comunque separate da un gap energetico tanto piccolo che gli elettroni non hanno alcuna difficoltà a saltare dall'una all'altra. Una volta passato in un orbitale del tutto vuoto, un elettrone non è più impegnato nel legame, e può quindi percorrere l'intero metallo senza difficoltà. Ciò vuol dire che il cristallo può essere percorso da una corrente elettrica. In altre parole, il materiale è un conduttore. Ciò spiega l'alta conducibilità elettrica presentata da tutte le sostanze metalliche.

Può essere però che le due bande (che vanno pensate come insiemi di orbitali con energie molto vicine tra loro, radunate in un intervallo brevissimo di energia) siano separate da un gap ΔE consistente, come in figura a fianco. Se il valore di ΔE è troppo elevato, nessun elettrone riesce a passare dalla banda di valenza a quella di conduzione, e si parla di isolanti. Ad esempio, nel diamante ΔE = 7 eV, ed esso non può condurre corrente, Se invece il valore di ΔE non supera 1,6 eV, è possibile far passare gli elettroni dalla banda di valenza in quella di conduzione con una ragionevole spesa di energia; questi materiali si dicono semiconduttori, cui dedicheremo i paragrafi seguenti.

8.3  L'età dei semiconduttori

Abbiamo visto che tra il Paradiso dei conduttori e l'Inferno degli isolanti vi è un Purgatorio, rappresentato dai semiconduttori. Sono tipicamente semiconduttori il silicio e il germanio, elementi del gruppo IV della tavola periodica, che possiedono quattro elettroni di valenza nell'orbitale più esterno. Mentre la resistività dei buoni conduttori si aggira sui 10^–2 Ω mm² / m e quella degli isolanti sui 10²⁰ Ω mm² / m, quella dei semiconduttori è dell'ordine di 10⁴ – 10⁵ Ω mm² / m. Inoltre, mentre la resistività dei conduttori metallici aumenta all'aumentare della temperatura (gli elettroni incontrano tanta maggior resistenza quanto più veloci si muovono gli atomi), nel caso dei semiconduttori la resistività diminuisce all'aumentare della temperatura. Perchè? E perchè i semiconduttori sono così importanti nella tecnologia odierna?

Le forze di legame nel reticolo cristallino del silicio e del germanio si originano dal fatto che ogni atomo è legato a quattro atomi circostanti mediante i suoi quattro elettroni di valenza. Nell'intorno dello zero assoluto non vi sono elettroni liberi, e i semiconduttori si comportano come isolanti. A differenza di questi ultimi, però, nei semiconduttori gli elettroni di valenza sono debolmente legati e, man mano che la temperatura cresce, un numero sempre maggiore di elettroni si libera dai rispettivi atomi a causa delle vibrazioni del reticolo cristallino, trasformandosi in elettroni di conduzione. Per questo la resistività decresce all'aumentare della temperatura.

Supponiamo ora di considerare una fila di atomi di silicio, come nell'immagine qui a destra. Se il primo di essi libera un elettrone nella banda di conduzione, si ionizza e si forma una lacuna, cioè un "posto vuoto" lasciato dall'elettrone vacante (vedremo nel § 9.6 che si tratta in effetti di una quasiparticella). Sotto l'azione di un campo elettrico, orientato nel nostro caso verso destra, un elettrone esterno dell'atomo adiacente può saltare nel primo atomo e "riempire" la lacuna. Così facendo, però, lascia una nuova lacuna nel secondo atomo. Anche il terzo atomo può liberare un elettrone che va a colmare la lacuna del secondo, ma a sua volta nel terzo si apre una lacuna. Se l'elettrone si muove verso sinistra, la lacuna sembra muoversi verso destra, e dunque nel campo elettrico esterno si comporta a tutti gli effetti come una carica positiva. La conduzione elettrica nel semiconduttore, insomma, è dovuta sia ad elettroni che si muovono verso sinistra, sia a lacune che si muovono verso destra. Mentre nei metalli i portatori di carica sono i soli elettroni negativi, nei semiconduttori sono sia cariche positive che negative. Siccome però i portatori liberi di carica nei semiconduttori puri sono pochi, la loro conducibilità elettrica è relativamente bassa. I semiconduttori puri di questo tipo vengono chiamati semiconduttori intrinseci; in essi il numero di elettroni di conduzione liberi è esattamente pari al numero di lacune.

Il comportamento dei semiconduttori in campo elettrico tuttavia cambia completamente se ad essi si aggiunge una piccola quantità di impurità con valenza diversa, pari a circa un atomo ogni milione di atomi di semiconduttore intrinseco. Supponiamo ad esempio di inserire nel reticolo cristallino del silicio degli atomi trivalenti come il boro, il gallio o l'indio. Ciascuno di questi atomi ha solo tre elettroni di valenza intorno a sé, come si vede qui sotto a sinistra, e dunque manca un elettrone nel reticolo cristallino; esso è sostituito da una lacuna, che si aggiunge alle lacune già esistenti nel semiconduttore intrinseco senza che venga liberato alcun elettrone di conduzione (gli elettroni di valenza sono indicati dai punti gialli). Il quarto legame si forma perchè il silicio cede un elettrone al boro, che perciò prende il nome di accettore. Si dice che il semiconduttore è stato drogato (il termine tecnico inglese è proprio "doping"!), e precisamente drogato di tipo p, perchè sono state aumentate artificialmente le lacune, cioè le cariche positive.

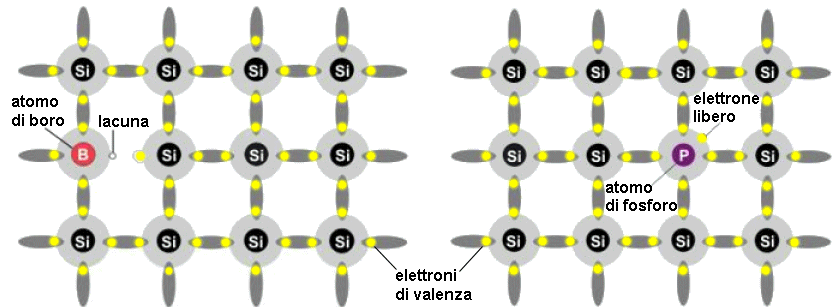
Se invece si mescola nel reticolo cristallino del silicio una sostanza pentavalente come il fosforo, l'arsenico o l'antimonio, ad aumentare sono gli elettroni di conduzione. Infatti ogni atomo di fosforo, come si vede sopra a destra, è circondato da cinque elettroni di valenza, dei quali quattro formano legami con altrettanti atomi di silicio, mentre il quinto viene liberato nella banda di conduzione senza la contemporanea formazione di una lacuna. Per ogni atomo di impurità si forma insomma un nuovo elettrone di conduzione che si aggiunge a quelli già presenti nel semiconduttore intrinseco. Gli atomi pentavalenti che si comportano come il fosforo sono detti donatori, perchè cedono ciascuno un elettrone alla banda di conduzione. Si parla in tal caso di drogaggio di tipo n, aumentando le cariche negative. I semiconduttori così drogati vengono chiamati semiconduttori estrinseci.

Quali applicazioni tecnologiche possiamo ottenere, con questi semiconduttori drogati? A scoprirlo furono tre grandi scienziati statunitensi del secolo scorso: John Bardeen (1908-1991), Walter Houser Brattain (1902-1987) e William Bradford Shockley (1910-1989), ricercatori della Bell Telephone. Essi considerarono anzitutto due porzioni di semiconduttore, drogate rispettivamente di tipo p e di tipo n, e le misero a contatto a formare una "giunzione". Nel semiconduttore drogato di tipo p le lacune sono più numerose degli elettroni, mentre in quello drogato di tipo n gli elettroni prevalgono sulle lacune. Attraverso la giunzione si ha una migrazione di elettroni dal semiconduttore di tipo n a quello di tipo p, e una di lacune dal tipo p al tipo n. Di conseguenza il semiconduttore drogato di tipo p assumerà una carica positiva e quello di tipo n una carica negativa, mentre fin qui erano tutti assolutamente neutri. Tra le due porzioni di semiconduttore si genera così una differenza di potenziale, che impedisce la successiva migrazione di elettroni e lacune.

Inseriamo ora una batteria collegandone il polo positivo al semiconduttore drogato di tipo p e il polo negativo al semiconduttore drogato di tipo n. Nel circuito così realizzato si avrà un passaggio di corrente, in quanto gli elettroni sono spinti attraverso la giunzione nel semiconduttore di tipo p, e le lacune in quello di tipo n. La differenza di potenziale che esisteva prima del collegamento tende a ridursi fino ad annullarsi, e la corrente si muoverà da p ad n praticamente senza incontrare resistenza. Se invece si collega il polo positivo della pila al semiconduttore di tipo n e quello negativo al semiconduttore di tipo p, la differenza di potenziale aumenterà e la corrente non potrà più circolare nel circuito. Il dispositivo a semi conduttori così realizzato insomma si lascia attraversare dalla corrente in un solo verso, e per questo motivo viene utilizzato come raddrizzatore di corrente. Esso assume il nome di diodo a semiconduttori. Quando esso fu realizzato esistevano già i diodi termoionici, ideati dall'inglese Owen Willans Richardson (1879-1959), che per questo ricevette nel 1928 il Premio Nobel, ma essi erano ingombranti, scaldavano parecchio (in pratica erano delle lampadine) e si bruciavano spesso e volentieri, mentre i diodi a semiconduttori sono molto più compatti, non scaldano, non richiedono energia per l'accensione e non dissipano calore, funzionando a temperatura ambiente. Qui sotto potete vedere lo schema e il simbolo circuitale di un diodo a semiconduttori.

I diodi sono conduttori non ohmici; si può dimostrare che l'intensità i della corrente può essere descritta, in funzione della differenza di potenziale V agli estremi del diodo, attraverso la seguente funzione, detta equazione del diodo:

dove i_s è la cosiddetta corrente di saturazione (minuscola corrente che attraversa la giunzione anche in caso di collegamento del semiconduttore drogato di tipo n con il polo positivo della pila), e è la carica dell'elettrone, K la costante di Boltzmann e T è la temperatura assoluta, mentre η è un coefficiente numerico che vale circa 2 per il silicio e circa 1 per il germanio.

Nel 1948 Bardeen, Brattain e Shockley misero a punto un ulteriore importantissimo dispositivo a semiconduttori, realizzato come segue. Essi realizzarono non una ma due giunzioni di semiconduttori: presero due porzioni di semiconduttore drogato p, dette rispettivamente emettitore e collettore, e interposero tra di esse uno strato sottilissimo (qualche centesimo di millimetro) di semiconduttore drogato n, detto base. Oltre ad avere uno spessore molto ridotto, la base è anche molto meno drogata dell'emettitore e del collettore. Il trio Bardeen - Brattain - Shockley collegò poi il polo positivo di una batteria con l'emettitore e il polo negativo con la base; presa una seconda batteria, ne collegò il polo positivo con la base e il polo negativo con il collettore, come si vede qui sotto. Si parla allora di giunzione p-n-p. I collegamenti così realizzati danno vita ad un moto di lacune che, partendo dall'emettitore, raggiungono la base, dove dovrebbero ricombinarsi con gli elettroni in eccesso ivi presenti. Ma la base è sottilissima e poco drogata; di conseguenza, poche lacune riescono a ricombinarsi con gli elettroni, e continuano invece la propria strada riversandosi nel collettore, aiutati dal campo elettrico che si stabilisce tra la base e quest'ultimo in virtù della seconda batteria.

La corrente che attraversa il collettore ha un'intensità maggiore rispetto a quella che passa nella base, poiché le lacune che attraverso la base giungono nel collettore incontrano nuove lacune, essendo il collettore drogato di tipo p. La seconda batteria infine attrae le lacune verso il polo negativo. Una tensione applicata tra emettitore e base produce in uscita, tra base e collettore, una tensione amplificata anche di un fattore 100! Quello che abbiamo realizzato è dunque un amplificatore di corrente, in analogia con il triodo termoionico realizzato nel 1906 dall'inventore americano Lee De Forest (1873-1961), ma esso presenta gli stessi vantaggi del diodo a semiconduttori: compattezza, lunga durata e bassissimo calore dissipato. Si parla perciò di triodo a semiconduttori. I suoi inventori però gli diedero un nome divenuto celeberrimo: "transfer resistor", cioè resistore di trasferimento, o più semplicemente transistor, destinato a rivoluzionare il mondo dell'elettronica. Qui sotto a sinistra vedete il primo transistor, presentato presso i Bell Labs il 23 dicembre 1947; la sua realizzazione fruttò a Bardeen, Brattain e Shockley il premio Nobel per la Fisica nel 1956. Bisogna aggiungere che John Bardeen è l'unico scienziato della storia ad aver vinto la bellezza di due Premi Nobel in Fisica, il primo nel 1956 per l'invenzione del transistor, e il secondo nel 1972 (come diremo nel § 8.7) per aver dato un'interpretazione quantistica del fenomeno della superconduttività, assieme a Leon Neil Cooper (1930-) e a John Robert Schrieffer (1931-), nota anche come teoria BCS dalle iniziali dei suoi scopritori! Tanto di cappello!

____

A destra si vedono invece i simboli circuitali del transistor p-n-p, in alto, e di quello di tipo n-p-n, in basso, nel quale emettitore e collettore sono drogati di tipo n, e la base è drogata di tipo p; l'unica differenza sta nel fatto che nell'n-p-n il verso della corrente emettitore-base è diretto dalla base verso l'emettitore. Le lettere E, C, B, indicano rispettivamente l'emettitore, la base e il collettore. È evidente l'analogia tra il transistor e il triodo termoionico, se facciamo corrispondere al filamento del secondo l'emettitore del primo, alla griglia del secondo la base del primo, e alla placca del secondo il collettore del primo. Nel triodo termoionico l'intensità di corrente è regolata dalla differenza di potenziale tra catodo e griglia, nel transistor dalla differenza di potenziale tra emettitore e base; in altre parole, nel transistor la base svolge un'azione di "controllo" sulla corrente che giunge nel collettore, come la griglia "controlla" gli elettroni che arrivano sulla placca nel triodo termoionico, ma con tutti i vantaggi elencati sopra rispetto alla tecnologia delle valvole termoioniche. Ad esempio, il transistor non ha bisogno di una tensione di accensione per la produzione di elettroni, in quanto esso possiede cariche in ogni momento, rappresentate dalle lacune e dagli elettroni di conduzione. L'energia consumata dipende perciò solo da quella erogata, mentre nel triodo termoionico bisogna mettere in conto un considerevole consumo di energia per accendere il filamento. Senza i transistor non sarebbe stato possibile realizzare tutti gli apparecchi elettronici che funzionano a pile, dalle radioline tascabili ai telefoni cellulari, perchè la tensione delle pile è insufficiente per alimentare una valvola termoionica. I transistor funzionano a basse tensioni, e non esistono i problemi di isolamento delle valvole connessi con le alte tensioni utilizzate. Anch'essi però presentano alcuni svantaggi: ad esempio non possono essere utilizzati nei circuiti in cui sono in gioco potenze molto elevate.

Qui sopra a sinistra si vede una foto di gruppo di Bardeen, Shockley e Brattain (da sinistra a destra rispettivamente) fotografati nei laboratori della Bell Telephone nel 1948; a destra si vede un mosaico del simbolo circuitale del transistor n-p-n realizzato sulla pavimentazione stradale davanti all'Università portoghese di Aveiro.

Bisogna aggiungere che la scoperta dei diodi e triodi a semiconduttori portò con sé quella del LED (in inglese "Light Emitting Diode", "diodo a emissione di luce"), i quali, grazie alla capacità di alcuni materiali semiconduttori di produrre fotoni attraverso un fenomeno di emissione spontanea, emettono un fotone ogni volta che un elettrone si ricombina con una lacuna, emettendo una luce continua, stabile, di elevata efficienza e lunga durata (la durata di un LED è di uno o due ordini di grandezza superiore a quella delle classiche sorgenti luminose, specie in condizioni di stress meccanici), di ogni colore desiderato e praticamente senza alcuna dispersione di calore. Il primo LED fu messo a punto nel 1962 da Nick Holonyak Jr. (1928-), e nel 2014 il Premio Nobel per la fisica è stato assegnato ad Isamu Akasaki (1929-) e Hiroshi Amano (1960-) della Nagoya University e a Shūji Nakamura (1954-) dell'Università della California a Santa Barbara per le loro ricerche sul LED a luce blu. Oggi i LED sono comunemente utilizzati per telecomandi a infrarossi, lampadine spia, indicatori di standby, retroilluminazione di display LCD, semafori stradali, dispositivi luminosi di autovetture e motocicli, cartelloni pubblicitari a messaggio variabile e segnalazione degli ostacoli al volo. In tempi recenti si sono diffusi anche come dispositivi di illuminazione, tanto che dal 2006 la città di Raleigh, nella North Carolina, è diventata la prima città del mondo interamente illuminata a LED! Qui sotto a sinistra vedete quattro esemplari di transistor comparati con le dimensioni di una comune moneta, mentre a destra vedete tre LED accesi.

____

Aggiungiamo che nel 1934, il grande fisico e matematico ungherese Eugene Wigner (1902-1995) aveva teorizzato la possibile esistenza di un cristallo fatto solo di elettroni. Solo nel giugno 2021 però due gruppi indipendenti di fisici hanno affermato di aver realizzato questi fantascientifici "cristalli di Wigner". Siccome gli elettroni si respingono l'un l'altro, essendo tutti negativi, un'idea per "immobilizzarli" in un reticolo potrebbe essere quella di raffreddarli, visto che il raffreddamento dovrebbe diminuire la loro energia e congelarli in un reticolo, proprio come l'acqua si trasforma in ghiaccio. Ma gli elettroni, si sa, si comportano come onde e, anziché fissarsi in una griglia ordinatamente disposta, tendono a scivolare e a scontrarsi contro i loro vicini. Un gruppo di ricerca guidato da You Zhou della Harvard University stava sperimentando il comportamento degli elettroni in una serie di fogli eccezionalmente sottili di semiconduttore separati da un materiale isolante. I fisici hanno raffreddato questi strati di semiconduttori fin oltre i ― 230 °C e hanno osservato che, quando vi era un certo numero di elettroni in ogni strato, essi erano tutti stranamente immobili in una matrice triangolare. Nel cristallo di Zhou, le forze repulsive tra gli elettroni in ogni strato e tra gli strati hanno disposto gli elettroni nella griglia di Wigner. Queste forze erano abbastanza intense da prevenire la fuoriuscita di elettroni, ma tale comportamento si verificava solo quando il numero di elettroni in ogni strato era tale da allineare le griglie del cristallo superiore e inferiore: i triangoli più piccoli in uno strato dovevano riempire esattamente lo spazio all'interno di quelli più grandi nell'altro. Anche un altro gruppo di ricerca, guidato da Ataç Imamoglu del Politecnico federale di Zurigo, ha usato questa tecnica per osservare la formazione di un cristallo di Wigner. Come abbiamo visto, l'unico problema che coinvolge gli elettroni e le forze elettriche che la Meccanica Quantistica sa risolvere in maniera rigorosa è quello di un singolo elettrone nell'atomo di idrogeno; negli atomi con molti elettroni, descrivere il comportamento degli elettroni interagenti diventa impossibile. Il problema dei molti elettroni interagenti è stato a lungo considerato uno dei più difficili della fisica, ed ora si spera che questi nuovi studi con l'aiuto dei semiconduttori ci aiutino ad escogitare nuovi modi per affrontare tale problema.

.

8.4  Da "Spazio 1999" ai qubit

L'introduzione dei transistor e di altri componenti ad essi simili permise di potenziare in maniera incredibile l'industria elettronica e, di conseguenza, di dare vita alla moderna industria informatica. Senza i dispositivi a semiconduttori, infatti, il visionario slogan di Steve Jobs e Steve Wozniak, fondatori della Apple ("un computer in ogni casa!"), non sarebbe stato realizzabile in pratica, viste le enormi dimensioni dei primi computer come l'ENIAC (1946), realizzato con la bellezza di 18.000 ingombrantissime valvole termoioniche! Qui sotto si vede lo schema di un circuito sommatore realizzato con due transistor (TR1 e TR2). Si può verificare che se i due segnali in ingresso (V_in) corrispondono entrambi a uno zero, anche quello in uscita (V_OUT) varrà zero; se uno dei due V_in vale 0 e l'altro vale 1, allora V_OUT = 1; se entrambi i V_in valgono 1, V_OUT = 10, secondo le regole della numerazione binaria.

Come tutti sappiamo, negli ultimi decenni l'elettronica ha conosciuto una straordinaria evoluzione, da un lato sviluppando componenti sempre più complessi ed avanzati, dall'altro riducendone in modo impressionante le dimensioni. Nell'epoca delle valvole termoioniche, un computer occupava un'intera stanza (chi non ricorda l'immenso computer della serie di fantascienza "Spazio 1999"?); grazie alla miniaturizzazione della tecnologia a semiconduttori, si è arrivati a realizzare cellulari con le funzionalità di un vero computer che stanno nel palmo di una mano, per non parlare degli I-watch della Apple, che ne concentrano tutte le funzioni in un orologio da polso! Qui sotto vedete questi due estremi della storia evolutiva della tecnologia informatica. A buon diritto è stato detto che, dopo l'età della pietra, l'età del rame, l'età del bronzo e l'età del ferro, oggi l'umanità si trova nell'età del silicio (o età dei semiconduttori), vista l'ormai totale dipendenza della nostra civiltà da questo tipo di tecnologia!

____

Ciò che ha reso possibile questo travolgente processo di miniaturizzazione è stato lo sviluppo dei cosiddetti circuiti integrati, i quali non utilizzano i transistor descritti in quel che precede, bensì i cosiddetti transistor MOS (Metal-Oxide Semiconductor). Si parla di circuiti "integrati" perchè non è più necessario realizzare separatamente singoli componenti (resistori, condensatori, diodi, transistor...) e poi montarli in un circuito: tutti gli elementi di un circuito complesso, connessioni incluse, possono essere realizzati direttamente su un'unica piastra di silicio. L'ideazione dei circuiti integrati la dobbiamo all'ingegnere americano Jack St. Clair Kilby (1923-2005), che nel 1958 ne costruì il primo esemplare composto da circa dieci componenti elementari. Per questa scoperta egli vinse il Premio Nobel per la Fisica nel 2000 (meglio tardi che mai).

La costruzione di un circuito integrato inizia da una barra di silicio ultrapuro, larga una decina di centimetri, dalla quale si tagliano lastrine sottilissime dette wafer. Dopo aver ottenuto uno strato superficiale di ossido di silicio, si ricopre il wafer con un preparato apposito, detto fotoresist, e gli si sovrappone una maschera, ottenuta fotograficamente da un disegno ingrandito del circuito da realizzare. Questa maschera permette di selezionare le porzioni del wafer alle quali devono essere aggiunte le impurità per drogarlo di tipo p e di tipo n; l'esposizione ai raggi ultravioletti modifica il fotoresist nelle zone non protette dalla maschera, conferendogli proprietà di durezza e resistenza agli acidi. Il fotoresist non esposto può essere eliminato facilmente prima di sottoporre il wafer ad attacco chimico con acido fluoridrico. Nelle zone non protette dal fotoresist, l'acido asporta l'ossido, e il silicio sottostante e pronto a ricevere il drogaggio e ad essere nuovamente ossidato. L'intero processo si ripete più e più volte con altre maschere, fino al completamento di tutti gli strati necessari. Alla fine, dopo aver asportato il fotoresist, si ricopre la lastra con uno strato di alluminio fatto evaporare sotto vuoto e, con un ultimo attacco chimico selettivo, si realizzano le connessioni elettriche. Da un wafer, che ha uno spessore di alcuni decimi di millimetro, si ottengono così centinaia di chip, ciascuno dei quali può contenere milioni di diodi e di transistor! Qui sotto a sinistra si vedono alcuni dei wafer da cui si ricavano i chip, mentre a destra si vede un microprocessore odierno per personal computer realizzato con questa tecnologia.

____

Le tappe di questo processo sono segnate dal numero di componenti circuitali integrati in ogni singolo chip:

• SSI (Small Scale Integration, integrazione su piccola scala): dal 1960 al 1965, con meno di 10 componenti;

• MSI (Medium Scale Integration, integrazione su media scala): all'inizio degli anni Settanta, da 10 a 100 componenti;

• LSI (Large Scale Integration, integrazione su larga scala): dal 1970 al 1980, da 100 a 10.000 componenti;

• VLSI (Very Large Scale integration, integrazione su larghissima scala): fino all'anno 2000, da 10.000 a 100.000 componenti;

• ULSI (Ultra Large Scale Integration, integrazione su scala ultralarga): negli anni duemila, fino a 10 milioni di componenti;

• WSI (Wafer Scale Integration, integrazione sulla scala di un wafer): tecnologia attuale, con la quale in un wafer può essere contenuto un intero computer!

I costi di realizzazione dei circuiti integrati si sono ridotti notevolmente nel tempo a causa di tecnologie sempre più efficienti ed automatizzate e alla forte economia di scala, ed essi sono divenuti ormai componenti elettronici circuitali a costo relativamente basso, permettendo di rendere economicamente accessibili strumenti digitali e analogici sempre più complessi, come gli odierni smartphone dei quali sembriamo non poter più fare a meno. Tali capacità di integrazione e quindi di calcolo rendono possibile l'utilizzo di applicazioni informatiche complicatissime come ad esempio quelle legate all'industria dei videogiochi oppure alla computer grafica, largamente sfruttata nei moderni lungometraggi di animazione.

Tuttavia le tecnologie attuali stanno ormai toccando i propri limiti fisici. Per esempio, in un circuito integrato le connessioni tra i milioni di componenti sono oggi ottenute con piste larghe soltanto qualche decina di nanometri: ridurle ulteriormente è tecnicamente difficilissimo, se si vuole mantenere l'affidabilità necessaria, perchè al di sotto di questa soglia si genereranno effetti "parassiti" indesiderati di natura quantistica nei circuiti elettronici. D'altra parte, in questi nostri anni Duemila sono stati costruiti circuiti microscopici che risultano molto più piccoli dei più piccoli tra i transistor, tanto che si parla ormai di elettronica molecolare. A questo proposito viene spesso citata la cosiddetta Legge di Moore, formulata empiricamente nel 1965 da David House (1945-), direttore esecutivo della Intel, commentando una precedente osservazione di Gordon Moore (1929-2023), cofondatore di Intel con Robert Noyce: secondo House, la complessità di un circuito integrato, misurata attraverso il numero di componenti per chip, raddoppia ogni 18 mesi. detto t il tempo in mesi ed N₀ il numero iniziale di componenti per chip, tale legge può essere facilmente espressa in termini matematici con la seguente espressione:

          (8.4)

Ad esempio, nel maggio 1997 Intel lanciò il processore Pentium II con 300 MHz di frequenza di clock e 7,5 milioni di componenti per chip. Nel novembre 2000, cioè 42 mesi dopo il lancio del Pentium II, Intel mise in vendita il Pentium 4 con frequenza di clock di 1,5 GHz e 42 milioni di componenti per chip. Applicando la Legge di Moore (8.5) si ha:

Secondo la Legge di Moore, dopo 42 mesi dal lancio del Pentium II sarebbe stato possibile realizzare un processore contenente 37,8 milioni di transistor. Come si vede, in questo caso, la legge ha stimato una crescita addirittura inferiore rispetto a ciò che è effettivamente avvenuto! Applicando la stessa formula non al numero di componenti ma alla frequenza di clock del processore si ha:

Stavolta la Legge di Moore ci ha dato come risultato 1500 Mhz, cioè proprio 1,5 GHz, la frequenza del Pentium 4. Qui sotto si vede una rappresentazione grafica della (8.4) in un diagramma logaritmico, che mostra come la Legge di Moore è stata sinora sostanzialmente rispettata. Facciamo osservare che, se anche il settore delle costruzioni fosse progredito con la stessa impressionante velocità, oggi saremmo in grado di costruire un grattacielo 35 volte più alto del monte Everest, e quindi alto qualcosa come oltre 300 chilometri!

Secondo molti ingegneri e progettisti i limiti estremi dell'integrazione dei circuiti sarebbero già stati raggiunti con la generazione dei processori Pentium, al di sopra del quale l'unico modo praticabile per aumentare le prestazioni di calcolo è rappresentato dalla tecnologia multicore, ovvero dall'accoppiamento in parallelo di più processori, come avviene nei supercalcolatori dei centri di calcolo, i quali hanno permesso tra l'altro di calcolare centinaia di milioni di cifre decimali del numero pi greco.

Per proseguire sulla strada dell'aumento della densità di transistori è necessario abbandonare l'odierna tecnologia a semiconduttori e inoltrarsi in un territorio affatto nuovo, quello dei cosiddetti computer quantistici. Essi rappresentano senz'altro la prossima frontiera dell'informatica, e potrebbero costituire un enorme salto di qualità rispetto alle previsioni della Legge di Moore. I computer elettronici attuali usano come unità fondamentale di informazione il bit (binary digit), unità che codificano due stati, aperto e chiuso (0 e 1) di un circuito; i computer quantistici utilizzeranno invece i qubit, unità di informazione quantistica codificati non da un valore univocamente prefissato di 0 o 1, ma dallo stato quantistico in cui si trova una particella o un atomo che può avere contemporaneamente sia il valore 0 sia il valore 1. Il termine qubit è stato introdotto dall'ingegnere statunitense Benjamin Schumacher del Kenyon College (Ohio). Come sappiamo, le particelle subatomiche possono trovarsi in una sovrapposizione di stati quantistici, e i qubit userebbero lo stato di polarizzazione dei fotoni o lo spin di atomi o molecole, a differenza dei bit classici che invece sono basati sulla presenza o assenza di una carica elettrica. Da un punto di vista matematico, un qubit è un punto di uno spazio vettoriale bidimensionale a coefficienti complessi, e precisamente un punto sulla superficie di una sfera di raggio unitario, detta Sfera di Bloch, Questa situazione amplierebbe enormemente le possibilità di codifica delle informazioni, aprendo la possibilità di sfruttare tale capacità di elaborazione per la risoluzione di problemi estremamente complessi, come quelli alla base dell'Intelligenza Artificiale (IA). Ad esempio, una particella quantistica può trovarsi per un 70 % nello stato 0 e per un 30 % nello stato 1. Questa caratteristica assume un significato incredibile se si pensa che due qubit possono avere 4 stati contemporaneamente, quattro qubit possono avere 16 stati, 16 qubit possono avare 256 stati, e così via. Se pensiamo al fatto che la quantità di informazione contenuta in N qubit è pari a 2^N bit classici (e quindi 2^N stati possibili), ci rendiamo conto che il computer quantistico sarà in grado di processare nello stesso momento più soluzioni ad un singolo problema, anziché svolgere calcoli sequenziali come avviene ora con l'elaborazione elettronica, ed eseguire calcoli complicatissimi impiegando secondi anziché anni per risolvere un problema! Inoltre l'ingresso della fisica quantistica nel mondo dell'elettronica permetterà la costruzione di dispositivi di tipo completamente nuovo, in grado di applicate la logica a tre valori (vero, falso, indefinito) propria della Meccanica Quantistica antiche la semplice logica aristotelica a due valori (vero, falso) degli attuali calcolatori digitali!

Ma come realizzare un computer quantistico? Oggi si pensa a due approcci possibili. Il primo, proposto da Robert Schoelkopf della Yale University di New Haven, nel Connecticut, sfrutta il raffreddamento dei circuiti vicino allo zero assoluto, in modo che funzionino come superconduttori senza resistenze che interferiscano sulla corrente; nell'ultimo paragrafo di questo capitolo vedremo che la superconduttività è proprio un fenomeno prettamente di natura quantistica. In questo caso si parla di "punti quantici" per indicare una nanostruttura di materiale semiconduttore inserita in un altro semiconduttore con intervallo di energia più grande. Una seconda metodologia, portata avanti da Christopher Monroe, fisico all'Università del Maryland a College Park, ricorre invece ad ioni "intrappolati" in campi elettromagnetici e manipolati affinché lo spostamento degli elettroni produca un cambiamento dello stato degli ioni, e quindi possa funzionare da qubit. Nella foto qui sopra potete vedere proprio una "trappola a ioni" per computer quantistici (foto di Kai Hudek, dell'Università del Maryland). Altre possibili proposte riguardano fotoni singoli e difetti puntiformi nei reticoli cristallini di diamanti. Tuttavia, nonostante l'ottimismo dei fisici, vi sono ancora alcuni problemi da risolvere, come la corretta manipolazione delle particelle che sono volatili e fragili, proprio perché cambiano stato, e potrebbero quindi comportare perdita di dati e informazioni utili al processo di calcolo, e naturalmente lo sviluppo di infrastrutture hardware idonee: oggi il raffreddamento dei sistemi richiede l'elio e le infrastrutture devono essere mantenute in ambienti privi di vibrazioni. Occorreranno anche algoritmi opportunamente sviluppati per il quantum computing, che oggi in parte appaiono ancora fuori della portata degli strumenti matematici di cui noi disponiamo.

Un passo avanti verso la realizzazione di computer quantistici è stato compiuto nel 2011 da alcuni ricercatori dell'Università di Pittsburgh, i quali hanno annunciato l'invenzione del transistor a elettrone singolo (o SET, Single Electron Transistor), nel quale la tensione applicata alla base permette di far passare dall'emettitore al collettore addirittura un elettrone alla volta, sfruttando il fenomeno quantistico dell'effetto tunnel attraverso le giunzioni del semiconduttore. L'idea parte da un'"isola" di atomi, capaci di trattenere un elettrone nel punto di convergenza di tre nanocavi sulla parte superiore di un substrato di alluminio. Una microscopica forza atomica crea un tunnel di elettroni attraverso i cavi e sopra l'isola di atomi, realizzando così un transistor con differenti stati di conduzione a seconda del numero di elettroni presenti su di esso.

E non è tutto. Nell'ottobre 2015 per la prima volta un gruppo di ricercatori dell'Università del New South Wales a Sydney ha realizzato una porta logica per qubit quantistici sfruttando sostanzialmente le stesse tecnologie usate per la fabbricazione dei chip di silicio dei computer diffusi oggi. Rendendo le connessioni fra porte logiche potenzialmente scalabili fino alle dimensioni tipiche di un computer reale. Le cosiddette porte logiche, che corrispondono alle operazioni logiche di base (come "AND", "OR", "NOT"), realizzate per i qubit hanno mostrato alcuni problemi, relativi o alla difficoltà di costruire le indispensabili grandi schiere di porte logiche, o alla possibilità di un loro controllo efficace, oppure alla stabilità dell'informazione nel suo passaggio attraverso di esse. Il fatto che il prototipo realizzato si basi in gran parte sulle tecnologie al silicio e che il comando delle porte logiche sia realizzato con semplici impulsi elettrici supera molti dei problemi che si frappongono alla realizzazione di computer quantistici. Nel 2019 poi una macchina composta da 54 qubit superconduttori ha eseguito il primo calcolo quantistico, che avrebbe richiesto tempi interminabili su un computer classico, un risultato che i ricercatori chiamano "vantaggio quantistico". Nel novembre 2021 la IBM, che ha investito molto nei qubit superconduttori, ha annunciato il successo del chip Eagle da 127 qubit, poi superato nel novembre 2022 dal chip Osprey da 433 qubit; e la IBM prevede di presentare entro il 2023 un chip quantistico chiamato Condor, destinato a superare la barriera dei 1000 qubit. Ovviamente l'obiettivo non è solo quello di aumentare il numero dei qubit, ma anche di migliorarne la qualità. Alcuni elementi superconduttori dell'IBM sono in grado di mantenere i loro stati quantistici per oltre 300 microsecondi, un record per questo tipo di tecnologia; inoltre è stato accertato che il 99,9 % delle operazioni che coinvolgono due qubit sono prive di errori, un traguardo davvero epocale.

Una tecnica che potrebbe presto infrangere la barriera dei 1000 qubit propone di intrappolare atomi neutri usando fasci laser strettamente focalizzati, chiamati tweezer ottici, e di codificare i qubit negli stati elettronici degli atomi o negli spin dei nuclei degli atomi. Per assemblare più qubit, i fisici dividono (in gergo si parla di "split") un singolo raggio laser in molti raggi, per esempio facendolo passare attraverso uno schermo fatto di cristalli liquidi. In questo modo si possono creare schiere di centinaia di "pinzette ottiche", ognuna delle quali intrappola il proprio atomo. Gli atomi sono tipicamente a pochi micrometri di distanza dai loro vicini, dove possono rimanere in uno stato quantico per diversi secondi o più. Per far interagire gli atomi, i fisici puntano un laser di quelli che hanno superato lo schermo su un atomo per sollecitarlo in uno stato eccitato, in cui un elettrone esterno orbita molto più lontano dal nucleo rispetto al normale. Questo aumenta le interazioni elettrostatiche dell'atomo con uno vicino. Usando le "pinzette", i ricercatori hanno realizzato schiere di oltre 200 atomi neutri, e stanno cercando di utilizzare questa nuova tecnologia per assemblare computer quantistici funzionanti. Altre tecnologie ancora più "fantascientifiche" prevedono di codificare le informazioni nello spin di singoli elettroni intrappolati da campi elettrici all'interno di semiconduttori convenzionali come il silicio. E c'è anche chi sogna dei computer fotonici, che puntano a sostituire interamente gli elettroni con fasci di luce per scambiare segnali e aumentare di un milione di volte la velocità dei computer e dei dispositivi mobili, ma a questo punto ci muoviamo davvero (per ora) nel campo della fantascienza.

Prima di cambiare argomento, ricordiamo la grande scoperta annunciato nel maggio 2019 da un gruppo di ricercatori dell'Università di Edimburgo, coordinato da Mark Evans: le cellule viventi sono come simili ai chip dei computer, nel senso che hanno una fitta rete di circuiti che connettono i loro diversi distretti. Questi circuiti di segnalazione sono stati osservati per la prima volta utilizzando potenti microscopi elettronici e simulazioni al computer simili a quelle adoperate dagli astrofisici nella ricerca che ha portato a ottenere la prima immagine di un buco nero. Secondo gli autori dello studio, le cellule sono in grado di modificare nel tempo questi circuiti in base alle funzioni da svolgere. Le informazioni  viaggiano grazie a molecole cariche, come ioni di calcio, su una rete di nanotubi, minuscoli circuiti che ricordano quelli del microprocessore di un computer. Questa rete di segnali locali orchestra l'insieme delle attività di una cellula. I segnali giungono anche al nucleo e sono in grado di modulare l'attività del DNA; attraverso questi circuiti interni le cellule sono capaci di riconfigurare, a seconda delle necessità e delle attività da compiere, l'accensione o spegnimento dei geni. Questo prefigura il sorgere di un altro dei sogni della fantascienza: il computer organico, ovvero la macchina vivente.

.

8.5  Il mistero dell'entanglement quantistico

Ma non basta. Finora le tecniche di creazione degli ologrammi (le rappresentazioni di oggetti tridimensionali, come le immagini di sicurezza stampate sulle carte di credito) si sono basate puramente sulla fisica classica, ma all'inizio del 2021 un gruppo di ricerca dell'Università di Glasgow, guidato da Hugo Defienne, ha pubblicato un lavoro che getta le basi dell'olografia quantistica e che potrà portare a nuove importanti applicazioni. Per realizzare un ologramma, l'olografia classica costruisce l'immagine dell'oggetto sfruttando 1'interferenza tra due fasci di luce laser coerenti, di cui uno viene usato per illuminare il soggetto, che si incontrano dopo aver percorso cammini ottici diversi. La tecnica proposta da Defienne e colleghi, pur partendo dalla stessa idea sperimentale, sfrutta invece proprio l'entanglement. In questo caso i due fasci laser che trasportano le informazioni necessarie a costruire l'immagine dell'ologramma contengono fotoni entangled, cioè correlati tra loro, che interferiscono tra loro senza incontrarsi, a differenza della tecnica classica. Secondo Defienne e colleghi, l'uso di fotoni entangled permetterà di realizzare ologrammi molto più dettagliati e ad alta risoluzione degli attuali, riducendone le imperfezioni. É un risultato che apre la strada a molteplici applicazioni, soprattutto nel campo della diagnostica per immagini, dove l'olografia può essere sfruttata per indagare funzioni biologiche e meccanismi non ancora osservati a livello delle cellule, e naturalmente in quello dei computer quantistici. E non finisce qui.

Non si può scrivere un libro dedicato ai misteri della Meccanica Quantistica senza citare un importantissimo dispositivo, il laser, che basa il suo funzionamento proprio sulle proprietà quantistiche della materia. "Laser" è l'acronimo dell'inglese "light amplification by stimulated emission of radiation" ("amplificazione della luce mediante emissione stimolata di radiazione"), e con questo termine si intende un dispositivo in grado di emettere un fascio di luce coerente, tale cioè che i suoi fotoni hanno tutti la stessa frequenza e la stessa fase iniziale, monocromatico e fortemente direzionale, capace cioè di non divergere anche per parecchi chilometri. In pratica il laser è uno strumento in grado di trasformare, mediante opportuni stimoli, le onde emesse da una sorgente luminosa convenzionale in una radiazione monocromatica e coerente.

Nel 1917 fu il solito Albert Einstein a formulare le basi teoriche del laser nell'articolo "Zur Quantentheorie der Strahlung" ("Sulla teoria quantistica delle radiazioni"), attraverso una nuova derivazione delle leggi sulla radiazione di Max Planck. Nel 1928 il tedesco Rudolf W. Ladenburg (1882-1952) dimostrò l'esistenza dell'emissione stimolata, che fu ottenuta per la prima volta sperimentalmente nel 1947 dagli americani Willis E. Lamb (1913-2008) e Robert Curtis Retherford (1912-1981). Il primo amplificatore per microonde ad emissione stimolata sull'ammoniaca, chiamato maser ("microwave amplification by stimulated emission of radiation"), fu messo a punto nel 1954 dagli americani Charles Hard Townes (1915-2015), James Power Gordon (1928-2013) e Herbert J. Zeiger (1925-2011): fu il primo amplificatore di radiazioni ad emissione stimolata. L'invenzione del laser è stata realizzata indipendentemente tra loro da più gruppi di ricerca: il 16 maggio 1960 Theodore H. Maiman (1927-2007) azionò il primo laser funzionante a Malibù in California presso i laboratori della Hughes Research; esso sfruttava il cristallo di rubino in grado di produrre un raggio laser rosso con una lunghezza d'onda di 694 nm. Contemporaneamente anche Nikolaj Gennadievič Basov (1922-2001) in Unione Sovietica giungeva allo stesso risultato. Sempre nel 1960 l'iraniano Ali Javan (1926-2016) e gli americani William R. Bennett (1930-2008) e Donald Herriott (1928-2007) costruirono un laser utilizzando l'elio ed il neon, in grado di produrre un raggio infrarosso coerente. Nel 1963 invece l'indiano Kumar Patel (1938-) dei Bell Laboratories mise a punto il laser ad anidride carbonica. Nel 1971 infine il giapponese Izuo Hayashi (1922-2005) e l'americano Morton B. Panish (1929-) sempre dei Bell Laboratories ottennero il primo laser a semiconduttori (diodo laser) in grado di operare con continuità a temperatura ambiente.

Ma come funziona il laser? Come sappiamo, se un atomo viene eccitato da un opportuno stimolo energetico, tende a ritornare allo stato di minima energia, chiamato stato fondamentale o "ground zero", mediante l'emissione di fotoni. Questo processo, detto diseccitazione atomica, può avvenire in due modi. Il primo, attraverso l'emissione spontanea, cioè il fenomeno con cui si origina la normale radiazione luminosa visibile. La diseccitazione spontanea degli atomi e un processo naturale in cui i quanti di luce vengono emessi casualmente in ogni direzione dello spazio (incoerenza spaziale) e in tempi diversi, cioè senza alcuna correlazione di fase (incoerenza temporale). Per esempio, se consideriamo le radiazioni emesse da una normale lampada ad incandescenza, i treni d'onda, derivando da un'emissione spontanea, sono sfasati fra loro, cioè sono incoerenti, e si propagano in diverse direzioni.

Il secondo meccanismo invece è quello dell'emissione stimolata: gli atomi eccitati sono stimolati ad emettere un fascio di radiazioni con le stesse caratteristiche spazio-temporali, cioè con la stessa lunghezza d'onda, con la stessa fase e collimato in una precisa direzione dello spazio. Ciò si può verificare quando gli atomi, preventivamente eccitati in stati metastabili, interagiscono con una radiazione di opportune frequenza, e quindi decadono in stati di minore energia con conseguente emissione di radiazione elettromagnetica, senza peraltro assorbire i fotoni della radiazione stimolante. In queste condizioni i contributi dei due treni di onde, rappresentati dai fotoni primari e dai fotoni indotti, si sommano, esaltando il processo di emissione. Per comprendere questo fenomeno si può ricorrere ad un esempio suggestivo: i fotoni di una radiazione incoerente possono essere paragonati ai bambini che, alla fine delle lezioni. escono da una scuola sparpagliandosi in tutte le direzioni con andatura diversa, mentre i fotoni di una radiazione coerente possono essere immaginati come un plotone di soldati che escono da una caserma tutti con lo stesso passo, perfettamente sincronizzati tra di loro!

Ma come funziona un dispositivo a luce coerente, per esempio il laser a rubino, che come visto ha rappresentato il primo laser a stato solido? L'apparato è essenzialmente formato da una cavità speculare nel cui interno sono inserite una lampada e un cristallo di rubino, varietà monocristallina dell'ossido di alluminio (Al₂O₃). La sorgente, detta lampada di pompaggio, innesca mediante un lampo di luce molto intenso l'eccitazione iniziale. Il cristallo di rubino, opportunamente dimensionato, rappresenta il materiale otticamente attivo, ossia il mezzo da eccitare; alle sue estremità vi sono due specchi paralleli, uno perfettamente riflettente, l'altro semitrasparente, per consentire la parziale emissione della radiazione coerente che si forma nella cavità. Oltre al rubino, sono numerose le sostanze che possono essere utilizzate come materiale otticamente attivo; la natura e lo stato di aggregazione del materiale attivo sono i principali fattori che distinguono fra loro i diversi tipi di laser (a stato solido, a gas, a liquido, a semiconduttore, ecc.).

La fase iniziale di eccitazione, provocata dal lampo emesso dalla lampada o da una scarica elettrica come nei laser a gas, viene chiamata fase di pompaggio, ed è caratterizzata dalla cosiddetta inversione di popolazione dei livelli energetici. Quest'espressione deriva dal fatto che, mentre prima dell'eccitazione la maggior parte degli atomi del mezzo attivo si trovano nello stato fondamentale, dopo l'eccitazione, prodotta dai primi quanti di luce o dalla scarica d'innesco e dai fotoni originati dalle prime diseccitazioni atomiche, gli atomi vengono "pompati" su un livello di energia superiore, cioè su uno stato eccitato. Tale stato è però metastabile, come un'asta tenuta in equilibrio su un dito in posizione verticale; non appena questi atomi vengono ulteriormente stimolati da altri fotoni, decadono con emissione di radiazione, senza però assorbirne: l'energia dei fotoni prodotta in questo decadimento si somma con quella dei fotoni incidenti. In pratica ogni fotone, muovendosi nel materiale attivo per un certo intervallo di tempo prolungato dalle molteplici riflessioni sulle superficie speculari, stimola mediante gli urti contro gli atomi eccitati, l'emissione di altri fotoni in cascata. Si parla in proposito di catena di moltiplicazione. Il percorso della catena di moltiplicazione, e quindi l'intensità del fascio, viene incrementato artificialmente mediante i due specchi paralleli che prolungano il tempo di permanenza dei fotoni nel materiale. Il funzionamento del tutto è ben illustrato da questa animazione:

Recentissima (risale al marzo 2019) è l'invenzione, da parte di un team di ricercatori dell'Istituto Nanoscienze del CNR, di un nuovo tipo di laser costituito da una rete di filamenti miniaturizzati di polimeri, da usare in sensori ottici ad alta efficienza. Il cuore di questo laser è costituito da un impalpabile intreccio di nanofibre polimeriche che emettono e amplificano la luce, al posto degli specchi dei laser tradizionali. Le nanofibre di materiale fotoattivo, con un diametro compreso tra i 200 e i 500 nanometri, emettono luce e poi funzionano come fibre ottiche lungo le quali questa si propaga: intrappolata nel reticolo lungo i percorsi di una matrice disordinata, la luce è soggetta a interferenze in centinaia di nodi ed emerge amplificata come luce laser. Da notare che i polimeri dei filamenti sono stati drogati con molecole organiche per conferire le proprietà di emissione ed amplificazione di luce all'intera rete.

Innumerevoli sono le applicazioni pratiche del laser, legate in particolare alla coerenza e alla direzionalità del fascio di luce così ottenuto. Utilizzando un laser di potenza a rubino, ad esempio, possiamo produrre cambiamenti di stato cosi localizzati da far evaporare quasi istantaneamente ogni materiale conosciuto. Per scopi industriali e tecnologici il laser viene usato per saldature normali e per microsaldature, per il taglio di molti materiali, per effettuare minutissimi fori del diametro di pochi micron, mentre nella ricerca scientifica il laser viene prevalentemente usato per studiare alcune microstrutture della materia, per indagare sugli effetti indotti dalle alte temperature, per produrre reazioni chimiche difficilmente ottenibili con le consuete tecniche, per l'analisi spettroscopica dei vapori emessi da una zona estremamente localizzata, e persino per cercare di provocare una fusione nucleare controllata in un plasma (vedi questa pagina per maggiori informazioni su quest'ultimo punto). Importanti sono anche le applicazioni nel campo delle comunicazioni terrestri e spaziali, nella meteorologia e soprattutto nella realizzazione di ologrammi tridimensionali. A scopi militari sono stati messi a punto sistemi laser di intercettazione balistica, mentre armi laser in grado di distruggere obiettivi in movimento restano per fortuna ancora confinate nella fantascienza.

Uno dei campi di applicazione più importanti del laser è però senza dubbio quello della medicina. Per la ridottissima area focale, per la facilita del controllo del fascio, per le proprietà micro-cauterizzanti (simultaneamente taglia e coagula), il laser rappresenta un prezioso strumento per moltissimi interventi di chirurgia, specie su tessuti altamente vascolarizzati, o di difficile accesso, o di ridotte dimensioni, quando è necessario conservare la funzionalità del tessuto dopo l'operazione, ad esempio nella neurochirurgia. In particolare il laser è utilizzato con successo in oftalmologia, ad esempio nella laserterapia retinica. Il laser è però utilizzato anche per i trattamenti di fotoepilazione e contro l'invecchiamento cutaneo. Il laser viene utilizzato come tecnica non invasiva anche per la rimozione di tumori allo stadio iniziale (terapia fotodinamica): nei tessuti viene iniettato una sostanza fotosensibile con un assorbimento selettivo nei tessuti malati. Al passaggio di un fascio di luce ad una determinata lunghezza d'onda, il farmaco attiva una reazione che ha per protagonista l'ossigeno, ossida e distrugge le sole cellule malate. Si noti che che il farmaco agisce selettivamente e le cellule sane non vengono intaccate, come avviene durante un'asportazione chirurgica.

>