

|
"La scienza, a confronto con la realtà, è primitiva, ma è la cosa più preziosa che abbiamo." Albert Einstein (1879-1955) |
.
9.1 Klein, Gordon e le energie negative
L'oscillatore armonico quantistico e l'atomo di idrogeno (ma la trattazione di quest'ultimo è troppo lunga e complessa per essere affrontata in questa sede) sono due dei pochi casi che permettono una completa risoluzione alle quadrature dell'equazione di Schrödinger. Nella stragrande maggioranza dei casi pratici, una soluzione analitica rigorosa è impossibile: come si è visto, non si può risolvere in modo esatto neppure l'atomo di elio, perchè tra i due elettroni si instaura una reciproca interazione di cui non si può non tenere conto, e che complica in modo irrimediabile le energie in gioco. Tuttavia è ipotizzabile una soluzione numerica delle equazioni per atomi polielettronici, ad esempio con il metodo di Hartree-Fock, che consenta di definire l'esatto ordine di riempimento delle shell atomiche.
C'è però una difficoltà. Anche il modello atomico quanto-ondulatorio si rivela alla lunga inadeguato alla descrizione corretta dei fenomeni microscopici. Infatti, si può dimostrare che l'equazione di Schrödinger per l'atomo di idrogeno ci permette di ricavare funzioni d'onda etichettate da tre soli numeri quantici: n, l, m, mentre noi abbiamo visto che il corretto riempimento ("aufbau") della Tavola Periodica richiede un quarto numero quantico, quello s di spin. Il magnifico castello costruito da de Broglie, Schrödinger, Born ed Heisenberg non riesce in alcun modo a spiegare la quantizzazione del momento magnetico intrinseco dell'elettrone; anzi, non riesce a spiegarne correttamente neppure l'esistenza! Infatti non è difficile rendersi conto che, se tale momento magnetico è dovuto a una pura e semplice rotazione sul proprio asse dell'elettrone, inteso come una sferetta di raggio pari al raggio classico, esso deve ruotare talmente veloce che i punti del suo equatore si muoverebbero a una velocità assai superiore a quella della luce, contro i fondamenti della Relatività Ristretta. Dunque la Fisica Atomica e la Fisica Relativistica vengono qui palesemente in conflitto tra di loro.
Ma non è tutto: proviamo a valutare la velocità dell'elettrone 1s dell'atomo di idrogeno. Secondo il modello ondulatorio, vale il Principio di Indeterminazione di Heisenberg:
Δp Δx ≈ h
Ma Δx è dell'ordine del raggio di Bohr a0, mentre Δp = me Δv. Ne segue:

È un valore non dissimile dai 2,2 x 106 m/s calcolati nella prima orbita di Bohr con il modello quantomeccanico. Siamo molto vicini alla velocità della luce, e perciò insorgono necessariamente degli effetti relativistici, come aveva già suggerito Sommerfeld per spiegare (classicamente) la separazione delle righe spettrali. Evidentemente non si può descrivere l'atomo, neppure il più semplice, cioè quello di idrogeno, senza tenere conto di questi effetti, pena l'impossibilità di una spiegazione corretta dei risultati sperimentali.
Il fatto è che il modello quanto-ondulatorio, come tutti i modelli, ha dei limiti e delle approssimazioni. Queste ultime riguardano la natura delle particelle, il tipo di interazione e la meccanica usata. Infatti le particelle come il protone che costituiscono il nucleo atomico hanno una struttura interna, e non risultano affatto puntiformi. Inoltre l'interazione non si propaga con velocità infinita, perchè più veloce della luce non può viaggiare nessuno. Dunque non è corretto dire che il potenziale è funzione solo della distanza! Di conseguenza è prevedibile che l'equazione di Schrödinger non descriva correttamente i livelli energetici dell'atomo di idrogeno, e che per questo dalla teoria ondulatoria non emerga lo spin dell'elettrone. La Meccanica Quantistica e quella Relativistica non sono semplicemente sommabili, ma è necessaria una teoria più generale, che inglobi entrambe unificandole. Dedicheremo quest'ultimo capitolo alla ricerca di tale teoria.

Oskar Benjamin Klein (1894-1977)
I primi a tentare l'impresa di unificare in modo soddisfacente le due teorie furono lo svedese Oskar Benjamin Klein (1894-1977) e il tedesco Walter Gordon (1893-1939), in base a un ragionamento concettuale molto semplice, anche se esso richiede necessariamente conoscenze molto avanzate di Analisi Matematica; chi non le possiede, salti direttamente alle conclusioni. Infatti l'equazione di Schrödinger (6.4):

può essere ricavata dall'equazione non relativistica della conservazione dell'energia meccanica totale:
per sostituzione dei cosiddetti operatori quantistici, come ci insegna la Meccanica degli Operatori, una delle formulazioni della Meccanica Quantistica:

Allora, per ottenere l'equazione d'onda per il moto di una particella la cui energia supera notevolmente la sua energia a riposo m c2, si deve partire dal legame relativistico tra energia ed impulso che, nel caso del moto libero di una particella, ha la forma:
Si veda a questo proposito il mio ipertesto "Il Treno di Einstein". Usando le sostituzioni precedenti si ha allora:

cioè:
Questa è l'equazione di Klein-Gordon, ricavata per la prima volta nel 1926, che si può anche riscrivere così:

L'operatore:

si dice operatore dalembertiano, dal nome del matematico francese Jean-Baptiste Le Rond d'Alembert (1717-1783), uno degli autori dell'"Encyclopédie". Esso permette di scrivere l'equazione delle onde (detta appunto equazione di d'Alembert) in maniera molto semplice, e grazie ad esso anche la (9.3) si può riscrivere:

L'operatore dalembertiano è la forma relativistica quadridimensionale dell'operatore laplaciano, se si pensa che ( i c t ) è la quarta coordinata dello spazio di Minkowski insieme a x, y, z, e che quindi ad essa corrisponde:

La (9.2) è scritta in assenza di forze, dunque è ragionevole che la (9.3) descriva il moto quantistico relativistico di una particella libera. Allora, se si cerca per essa una soluzione del tipo:
![]()
si verifica che essa soddisfa la (9.3) per valori dell'energia pari a:
dove, ovviamente:
![]()
La (9.4) equivale in tutto e per tutto alla (9.2). Tuttavia, è evidente che nasce una difficoltà. Infatti secondo la (9.4) abbiamo sia dei livelli positivi che dei livelli negativi di energia, ed invece si sa che una particella libera può avere soltanto energie positive. Dunque dalla teoria quantistica relativistica comincia ad emergere qualcosa di nuovo, mai visto prima! Se sostituiamo la (9.4) nella (9.3), scopriamo due soluzioni corrispondenti a due diversi segni dell'energia, che per convenzione chiameremo rispettivamente Ψ+ e Ψ–. Ciò è fondamentale per comprendere il concetto di antiparticella.
Se infatti indichiamo con E+ ed E– gli autovalori dell'energia corrispondenti alle due funzioni d'onda Ψ+ e Ψ–, per essi potremo trovare le due espressioni analitiche:

dove E è data dal modulo della (9.4). Si può dimostrare che la densità di carica elettronica ρe per unità di volume nello spazio è dato allora dalla formula:

e quindi tale densità può essere sia positiva che negativa! Quelle descritte dalla funzione d'onda Ψ+ sono le comuni particelle, mentre quelle descritte dalla funziona d'onda Ψ– si dicono antiparticelle. L'operazione che ad una particella come l'elettrone fa corrispondere la sua corrispondente antiparticella si chiama coniugazione di carica, perchè le due funzioni d'onda Ψ+ e Ψ– sono l'una la coniugata dell'altra. Tutto questo emerge già molto bene dalla semplice equazione di Klein-Gordon.
.
Non è però difficile rendersi conto che tale equazione non è in grado di descrivere il comportamento relativistico dell'elettrone nell'atomo di idrogeno, perchè le particelle la cui funzione d'onda sono soluzioni della (9.3) sono prive di momento magnetico proprio. Dunque, dall'equazione di Klein-Gordon non è possibile ricavare lo spin: essa descrive particelle a spin nullo, come i pioni (π+, π–, π0), mesoni teorizzati nel 1935 da Hideki Yukawa (1907-1981) e osservati nel 1947 nei raggi cosmici, e i kaoni (K+, K–), osservati nel medesimo anno: molti anni dopo la formulazione della suddetta equazione, dunque. Il problema dello spin elettronico restava così insoluto.
Paul Adrien Maurice Dirac (1902-1984)
Il grande merito di aver trovato la soluzione corretta di questo complicato rompicapo teorico spetta all'inglese Paul Adrien Maurice Dirac (1902-1984), brillante fisico matematico da annoverare fra i più geniali intelletti del secolo. Egli ragionò nel modo che segue. Nella Fisica Relativistica le tre coordinate spaziali e la coordinata temporale (i c t) sono assolutamente equivalenti tra di loro; dunque non c'è alcun motivo per cui nelle equazioni del moto esse compaiano con diverso ordine di derivazione. Invece l'equazione di Schrödinger contiene le derivate seconde rispetto alle tre coordinate spaziali, e la derivata prima rispetto al tempo. Del resto, essa è ricavata dalla meccanica newtoniana classica, in cui l'energia (più precisamente E / c) e le componenti della quantità di moto (px, py, pz) non sono le componenti di uno stesso vettore, ma sono grandezze ben diverse tra di loro, così come lo sono lo spazio e il tempo. Klein e Gordon avevano provato ad introdurre nelle equazioni delle onde tutte e quattro le derivate seconde rispetto a x, y, z e t, ma non erano riusciti a far emergere lo spin. Allora, invece di sostituire alla derivata prima rispetto al tempo la derivata seconda, pensò Dirac, perchè non sostituire alle derivate seconde rispetto alle coordinate spaziali le derivate prime? Naturalmente egli dovette introdurre altre unità immaginarie, ma ciò non è un problema; l'importante è che gli autovalori dell'energia abbiano la forma data dalla (9.4). Al limite, si deve avere:
![]()
Mettiamoci allora nel caso unidimensionale, il più semplice, e cerchiamo due coefficienti α e β tali che:
Se px ≠ 0 ed m ≠ 0 contemporaneamente, generalmente non esisteranno valori numerici di α e di β che soddisfano la (9.5). Infatti, elevandone entrambi i membri al quadrato, si ha:
![]()
Essa è verificata se e solo se si ha contemporaneamente:

Chiaramente nessun numero finito, né reale né immaginario, soddisfa queste tre relazioni. Però, pensò Dirac, se α e β fossero matrici, le cose cambierebbero radicalmente! Infatti, posto:

si ha:

Naturalmente il prodotto d matrici in generale non è commutativo, per cui risulta α ≠ β. L'equazione quantistica relativistica cercata deve dunque avere coefficienti matriciali! Nel caso tridimensionale, alla (9.5) va sostituita la seguente:
In questo caso le condizioni diventano:

con j, k = 1, 2, 3 e j ≠ k. Stavolta le matrici sono necessariamente quadridimensionali! Le soluzioni sono del tipo:

Questi coefficienti permettono di esprimere la (9.6) nella forma:
![]()
Sostituendo ad E, px, py, pz i corrispondenti operatori quantistici, Dirac ottenne:

e dopo facili semplificazioni:
Questa è la cosiddetta equazione di Dirac, ed è l'equivalente relativistico dell'equazione di Schrödinger; effettivamente essa contiene solo le derivate prime rispetto a x, y, x, t. Teniamo conto del fatto che si tratta di un'equazione matriciale, i cui coefficienti α1, α2, α3, β sono matrici, e precisamente matrici hermitiane, che cioè coincidono con le coniugate delle proprie trasposte: una caratteristica comune, questa, a tutte le matrici che esprimono operatori quantistici. Sono inoltre indipendenti tra di loro, e si possono scrivere nella forma seguente:

dove 0 è la matrice nulla, I è la matrice identità:

e le tre matrici σj (j = 1, 2, 3) sono dette matrici di Pauli:

Esse soddisfano le relazioni:
![]()
dove j, k l, assumono i valori 1, 2, 3 a rotazione. Inoltre, σj2 = I, qualunque sia j. È un po' strano vedere delle matrici i cui elementi sono matrici, ma oramai in Meccanica Quantistica siamo abituati a vederne di tutti i colori!
Si è sottolineato il fatto che l'equazione (9.7) è un'equazione matriciale, i cui coefficienti sono matrici e la cui incognita è un vettore a quattro componenti, nelle quattro direzioni dello spazio-tempo:

Sviluppando le matrici, l'equazione di Dirac (9.7) equivale alle quattro seguenti equazioni scalari:

Ci si può chiedere: dato che la funzione d'onda è sempre stata trattata da noi come uno scalare, come mai ora è diventata un vettore, per giunta a quattro componenti? Siccome l'equazione di Klein-Gordon prevede l'esistenza di antiparticelle, è evidente che esse devono saltar fuori anche dall'equazione di Dirac, che ne costituisce un perfezionamento. Dunque, necessariamente due componenti della funzione d'onda restituiranno le particelle, e le altre due le antiparticelle. Ma, anche così, sia a un corpuscolo che al suo omologo con carica inversa noi assegniamo due componenti. Come si spiega questo enigmatico fatto? Si può dimostrare che esse sono dovute ai due stati di spin.
Infatti un elettrone può avere spin up o spin down. Chiamiamo Ψ↑ e Ψ↓ le funzioni d'onda che corrispondono a tali diversi stati elettronici. Ora, la Meccanica degli Operatori messa a punto proprio da Dirac ci insegna che misurare la componente lungo z del momento angolare di spin significa applicare alla funzione d'onda il corrispondente operatore quantistico. Chiamiamo Ŝz tale operatore. La misura può restituire solo i due valori + h / 4 π e – h / 4 π; essi saranno i cosiddetti autovalori dell'operatore Ŝz, corrispondenti alle autofunzioni Ψ↑ e Ψ↓. In altre parole:

che si possono sintetizzare così:
![]()

|
La formula di Einstein E = m c2 rappresentata sopra il grattacielo Taipei 101 (Taiwan) in occasione del centenario della sua formulazione |
Ma che forma ha l'operatore di spin, da noi finora mai incontrato? Proviamo a scrivere Ŝz nella forma:
Infatti una matrice, se moltiplicata per (applicata ad) un vettore, è a tutti gli effetti un operatore. Se le funzioni d'onda di spin hanno la forma:

avremo immediatamente:

Sembra proprio che abbiamo imboccato la direzione giusta. Non è difficile accorgersi che:

Dunque la terza matrice di Pauli σ3 coincide con l'operatore Ŝz. Analogamente si potrebbe provare che gli operatori Ŝx ed Ŝy, relativi alle altre due componenti del vettore s, sono dati da:

D'altro canto, osserviamo che la più generale funzione d'onda di spin si può esprimere come combinazione lineare di Ψ↑ e di Ψ↓ con coefficienti a e b generici:

Perciò è possibile interpretare questi vettori come sovrapposizione di stati quantistici: [ 1 0 ]T indica che ho una componente up e nessuna componente down, [ 0 1 ]T indica che ho una componente down e nessuna componente up.
Per avere la certezza che la nostra rappresentazione è corretta ricordiamoci che, come esprime la (3.8) nel § 3.7, il momento magnetico è direttamente proporzionale al momento angolare. Dato che anche lo spin è un momento magnetico, quello associato allo spin dell'elettrone sarà dato da:

In essa, la costante di Planck è stata inglobata nel vettore s. L'energia dello spin in un campo magnetico uniforme B allora è data da:

Come abbiamo detto, la Meccanica degli Operatori formulata da Dirac nel 1926 richiede che a tale grandezza associamo un operatore quantistico. La corrispondente equazione di Schrödinger in forma operatoriale è allora la seguente:

Se il campo è diretto lungo l'asse z, per la (9.8) si ha l'equazione matriciale:

che si scinde in due:
Come soluzioni scegliamo le due seguenti:

e sostituendole nelle (9.9) troviamo:

Ne consegue che la soluzione generale dell'equazione matriciale è del tipo:

Osserviamo che ( e Bz / me ) ha le dimensioni dell'inverso di un tempo, e quindi possiamo chiamarlo ω0. Ora, se calcoliamo il valor medio o valore di aspettazione della componente sz dello spin lungo z, indicato da Pauli con il simbolo < sz >, usando gli strumenti della Meccanica degli Operatori si trova:

Tale valore medio è indipendente dal tempo, perchè l'esponenziale immaginario sparisce. Operando allo stesso modo si ricava:
![]()
Queste componenti, come si vede, dipendono dal tempo. Se ne ricava che la componente dello spin nel piano xy ruota con velocità angolare ω0, perchè:
![]()
Resta così giustificato quello che viene chiamato il modello vettoriale dello spin, formulato nel 1925 dai fisici olandesi George Eugene Uhlenbeck (1900-1988) e Samuel Abraham Goudsmit (1902-1978), secondo il quale lo spin elettronico è rappresentato da un momento magnetico che precede intorno all'asse z, come illustra lo schizzo sottostante:

Infatti, la componente sz lungo l'asse z resta costante, mentre la "freccia" del vettore s percorre una circonferenza. Se a = 1 e b = 0, si ha Ψ = Ψ↑ e sz = h / 4 π; se a = 0 e b = 1, invece, si ha Ψ = Ψ↓ e si ha sz = – h / 4 π. Osserviamo infine che l'operatore modulo quadrato dello spin è dato da:

dove I è la matrice identità. La corrispondente equazione operatoriale è:

E poiché si ha:

la precedente può essere riscritta:
![]()
con ms = 1 / 2. Il modulo dello spin pertanto può assumere solo i valori:
![]()
espressione da noi già presentata nel § 3.8, come certamente ricorderete. Le ipotesi di Wolfgang Pauli sulla quantizzazione del momento angolare intrinseco dell'elettrone trovano pertanto una perfetta interpretazione nell'ambito della teoria quantistica relativistica di Paul Dirac!

Wolfgang Pauli (1900-1958), autore della teoria dello spin
.
9.3 Il modello atomico quanto-relativistico
Osserviamo che la (9.7) può essere riscritta a sua volta nella forma operatoriale:
formalmente analoga alla forma operatoriale (6.5) dell'equazione non relativistica di Schrödinger, a patto di definire l'operatore hamiltoniano di Dirac:

Imponendo una soluzione del tipo:

si ricava per ψ(r) la seguente equazione:
Questa è l'equazione per gli stati stazionari relativistici, analoga alla (6.8). I livelli energetici sono ancora gli autovalori dell'operatore hamiltoniano relativistico ĤD. Siccome la carica può essere positiva o negativa (a seconda che si parli delle particelle o delle relative antiparticelle), si introduce un nuovo grado di libertà nel possibile stato assunto dalla nostra particella. Conviene perciò rompere la funzione d'onda ψ(r), che poi è un vettore a quattro componenti, nella somma di due vettori φ(r) e χ(r) a due componenti, uno per la particella e uno per l'antiparticella:

Allora l'equazione (9.11) può essere rotta in due equazioni distinte. Infatti, utilizzando le definizioni di αj e β mediante le matrici di Pauli σj, si ha:

il che equivale al sistema:

ovvero:

Questo è palesemente un sistema omogeneo. L'algebra matriciale ci dice che esso ammette soluzioni non nulle solo se si annulla il determinante dei coefficienti delle funzioni incognite:

Si osservi che questo è un determinante di operatori! Esso equivale a:

e passando dagli operatori alle grandezze fisiche:

Sviluppando
 , e ricordando che
σj2
= I, mentre:
, e ricordando che
σj2
= I, mentre:

si ottiene l'espressione:
![]()
Gli autovalori dell'energia sono dunque:
![]()
Questa formula coincide con la (9.4), cioè con gli autovalori dedotti dall'equazione di Klein-Gordon! Non è difficile, d'altro canto, dimostrare che l'equazione di Dirac e l'equazione di Klein-Gordon ammettono le stesse soluzioni nel caso di particella libera. In questo caso infatti la (9.7) è soddisfatta per:
dove ψ0 è un vettore di quattro costanti. Infatti, se il moto è supposto avvenire lungo l'asse z, si può scrivere:
![]()
e sostituendola nell'equazione di Dirac si trova il sistema:

Sviluppando il determinante si scopre che la condizione per avere soluzioni non banali è:
![]()
cioè:
![]()
Gli autovalori sono dunque:
![]()
che coincidono con i (9.4) se:
![]()
Ora applichiamo l'operatore
 ad
entrambi i membri della (9.10):
ad
entrambi i membri della (9.10):

Ma gli operatori ĤD ed
 sono
tra di loro commutabili, perchè ĤD non agisce sul tempo, né
sono
tra di loro commutabili, perchè ĤD non agisce sul tempo, né
 sulle
coordinate spaziali. Possiamo perciò riscrivere la precedente come segue:
sulle
coordinate spaziali. Possiamo perciò riscrivere la precedente come segue:

Operando opportunamente con le matrici σj, si verifica che:
![]()
cosicché la nostra equazione diventa:

cioè:

che è proprio l'equazione di Klein-Gordon (9.3)! Dunque le componenti della (9.12) soddisfano anche l'equazione per particelle a spin nullo. La differenza sta nel fatto che l'equazione di Dirac, se risolta per l'atomo di idrogeno, fornisce esattamente lo spin dell'elettrone, prevedendo esattamente tutti i livelli energetici e le suddivisioni delle righe spettrali che avevano resistito a qualunque tentativo di interpretazione nel modello quanto-ondulatorio. A questo scopo bisogna correggere l'hamiltoniano relativistico ĤD con opportuni operatori che tengano conto del potenziale del campo di forze centrali avvertito dall'elettrone nel suo moto attorno al nucleo, non compreso nella (9.7). Il risultato permette di interpretare perfettamente la struttura fine dell'atomo di idrogeno e di quelli più pesanti: si parla al proposito di modello quanto-relativistico dell'atomo. Esso riesce a spiegare in modo molto soddisfacente il comportamento dell'atomo in campo elettrico (effetto Stark) e in campo magnetico (effetto Zeeman anomalo). Anch'esso però lascia aperti dei problemi, e in particolare quello delle energie negative.

George Uhlenbeck (1900-1988) e Samuel Goudsmit (1902-1978)
.
9.4 Il mare di Dirac e l'antimateria
Infatti dall'equazione di Klein-Girdon e dall'equazione di Dirac emerge con chiarezza l'esistenza di livelli di energia negativa anche per la particella libera. Questo fatto costituisce una grossa difficoltà concettuale, perchè un elettrone tende sempre a trovarsi nel livello di energia più basso che gli è concesso di occupare. Allora tutti gli elettroni, con energie normalmente positive, dovrebbero precipitare sui livelli ad energia negativa, e alla fine si troverebbero tutti in questo "baratro energetico". Ciò evidentemente non si verifica, perchè gli elettroni liberi con energia positiva restano tutti dove sono, se non ci sono altri livelli ad energia positiva ma inferiore su cui saltare! Ci troviamo di fronte all'ennesima contraddizione tra previsioni teoriche e realtà sperimentale.
Paul Dirac però non si scompose. Invece, egli ragionò in questo modo: se gli elettroni non saltano su livelli di energia negativa, vuol dire semplicemente che essi sono già tutti occupati. In base al Principio di Esclusione di Pauli, ogni livello energetico può essere occupato solo da due elettroni, con spin opposto. Se allora tutti gli infiniti livelli energetici con E < 0 sono già occupati da due elettroni, come mostra lo schizzo sottostante, i salti dai livelli di energia positiva risulteranno inammissibili, esattamente come nell'atomo di idrogeno un elettrone non può passare dalla shell L alla shell K, se questa è già occupata da due elettroni. Ma se tutti gli infiniti livelli di energia negativa sono già occupati, bisogna concepire il vuoto come un mare di elettroni di energia negativa, detto appunto mare di Dirac.
È possibile rilevare queste particelle di energia negativa? No, perchè con nessun apparecchio elettrico è possibile rivelare una distribuzione uniforme di cariche nello spazio, per quanto densa essa sia. Per comprendere questo concetto, si pensi ad un pesce che nuota nel mare, che non è mai stato in superficie e non ha mai toccato il fondo. Supponendo trascurabile l'attrito dell'acqua contro le sue pinne, esso non può stabilire se nuota nell'acqua, nell'aria o nel vuoto assoluto; e si sa che ciò che non si può osservare, non interessa alla Fisica. Tuttavia, secondo Dirac è possibile rivelare indirettamente un effetto di questo mare elettronico. Infatti, se un elettrone con E > 0 non può saltare verso il basso, uno con E < 0 può invece essere eccitato e saltare verso l'alto. Siccome in base alla (9.4) il valore minimo del modulo degli autovalori dell'energia è m c2, se io fornisco a un elettrone di energia negativa un'energia pari almeno a ( 2 m c2 ), questo salta su un livello con E > 0 non occupato, e diventa rivelabile! Come si vede nello schizzo qui sotto, al suo posto sul livello da cui l'elettrone è partito rimane una lacuna (proprio come nei semiconduttori di cui si è parlato nel § 8.3). Prima dell'evento il mare di Dirac era considerato elettricamente neutro, perchè le cariche elettroniche negative devono essere compensate dalle cariche delle particelle positive, i protoni, i quali verificano anch'essi l'equazione di Dirac, e riempiono quindi un mare di Dirac di protoni con energia negativa. Se però scompare una carica negativa in un mare elettricamente neutro, rimane una carica negativa in più, e quindi la lacuna si comporta come una carica positiva (anche in questo caso, in evidente analogia con i semiconduttori). Tale lacuna si comporta proprio come una particella, e coincide con l'antiparticella prevista dall'equazione di Dirac.

Inizialmente Dirac pensava che questa antiparticella dovesse coincidere con il protone, la carica positiva costituente il nucleo atomico. Ma, se così fosse, l'elettrone che ruota attorno a un protone nell'atomo di idrogeno salterebbe subito nella "lacuna" da esso costituita, emettendo la differenza di energia sotto forma di radiazione, e l'atomo risulterebbe instabile. L'ipotesi del mare di Dirac suscitò dunque molte perplessità fino al 1932, quando l'americano Carl Anderson (1905-1991) riuscì ad osservare che gli elettroni dei raggi cosmici, quando attraversano un campo magnetico, in parte sono deviati nella direzione prevista dalla teoria (tenendo conto che si tratta di particelle negative), e in parte... nella direzione opposta! Ciò era spiegabile solo ammettendo l'esistenza di elettroni positivi, da Anderson battezzati positroni, che sono del tutto identici agli elettroni scoperti da J.J. Thomson, fuorché nella carica elettrica. Essi si comportano esattamente come dovrebbero fare le "lacune" nel mare di Dirac. Era stata così rivelata la prima antiparticella. Qui sotto si vede la fotografia del primo positrone mai osservato, ottenuta nel 1932 da Carl Anderson e tratta da "The Positive Electron", Physical Review 43 (6): 491-494.

Subito i ricercatori si misero al lavoro, e bombardando piastre metalliche con raggi gamma molto duri riuscirono a creare coppie elettrone-positrone. Questo fenomeno, noto come creazione di coppie, è un esempio della trasformazione dell'energia in massa, prevista dalla famosa equazione E = m c2 della Relatività Ristretta di Einstein (vedi il mio ipertesto "Il Treno di Einstein"). Poiché un elettrone e un positrone hanno ciascuno una massa di 9,1 x 10–31 Kg, per un totale di 1,82 x 10–30 Kg, a tale massa corrisponde un'energia di:
1,82 x 10–30 Kg x ( 3 x 108 m/s)2 = 1,638 x 10–13 J = 1,022 x 106 eV
dove un elettronVolt (eV) è pari ad 1,6 x 10–19 J. Ne consegue che la creazione della coppia elettrone-positrone ha luogo solo se il fotone che si "materializza" ha un'energia di almeno 1022 KeV. Applicando la legge di Planck E = h f troviamo che tale energia corrisponde ad una frequenza di 2,46 x 1020 Hz, cioè ad un fotone nella banda dei raggi gamma duri. Quella di 1022 KeV è chiamata energia di soglia per la creazione di coppie, e ha una grandissima importanza nella progettazione di schermi antiradiazioni.
Al contrario, quando un elettrone e un positrone entrano in contatto, è come se il primo "rientrasse" nella lacuna rappresentata dal secondo, ed allora emette il dislivello energetico fra i due, di 1022 KeV per l'appunto, generando due fotoni gamma da 511 KeV ciascuno che partono in direzioni opposte: si parla in tal caso di annichilazione della coppia, anche se il termine è un po' fuorviante. Esso infatti deriva dal latino "nihil", "niente", mentre l'elettrone e il positrone non si sciolgono nel nulla: si convertono in energia della radiazione. In entrambi i casi, creazione di coppie ed annichilazione, il principio di conservazione della massa e dell'energia è insomma rispettato, come aveva previsto Einstein.

Nel 1955 l'italiano Emilio Segrè (1905-1989), lavorando con l'americano Owen Chamberlain (1920-2006) sulle interazioni protone-protone ad alta energia all'acceleratore di particelle Bevatron di Berkeley, ottenne la produzione del primo antiprotone, risultato per cui Segrè e Chamberlain furono insigniti del Premio Nobel, ma la cosa è stata molto più difficile della generazione di positroni, perchè la massa a riposo del protone supera di 1840 volte quella dell'elettrone, e dunque anche le energie in gioco sono più elevate. Per ottenere una coppia protone-antiprotone sono necessari infatti 1876 MeV di energia, ottenibili solo nei più potenti acceleratori di particelle. Un anno dopo gli antiprotoni vennero ottenuti anche i primi antineutroni, grazie al lavoro di Bruce Cork (1916-1994). Il dubbio è: essendo privi di carica, gli antineutroni non coincidono con i neutroni? Oggi sappiamo che la risposta è no, perchè particelle e antiparticelle non differiscono solo per la carica elettrica, ma anche per il momento magnetico e per la composizione interna. Solo i bosoni (fotone, gravitone...) coincidono con le loro particelle. Ettore Majorana (1906-?) ipotizzò che esistessero fermioni che coincidono con le loro antiparticelle, oggi chiamati in suo onore fermioni di Majorana, ma a tutt'oggi non ne è stato scoperto nessuno. Che i neutrini siano fermioni di Majorana è solo un'ipotesi sinora mai confermata. L'esperimento NEMO-3, in corso dal 2003 sotto il traforo del Frejus, è stato organizzato per accertare se il doppio decadimento beta può avvenire in assenza di neutrini; in caso positivo, questo proverebbe che il neutrino è un fermione di Majorana.
Naturalmente l'esistenza di positroni e di antiprotoni fece nascere il dubbio che esistessero anche antiatomi, cioè atomi con un nucleo negativo ed orbitali positivi; ed in effetti nel 1965, al CERN di Ginevra, il gruppo di ricerca condotto da Antonino Zichichi (1929-) produsse il primo nucleo di antideuterio, e nel 1978 ricercatori italiani e francesi guidati da Giorgio Giacomelli (1931-2014) scoprirono nuclei di antitrizio. Nel 1995 nell'acceleratore di particelle LEAR (Low Energy Anti-Proton Ring) al CERN di Ginevra vennero prodotti per la prima volta atomi di anti-idrogeno facendo collidere antiprotoni prodotti in un acceleratore di particelle contro cluster di xeno. I primi atomi di anti-idrogeno sintetizzati avevano una temperatura molto elevata (alcune migliaia di kelvin), quindi avevano una grande energia cinetica che li portava in breve tempo a colpire le pareti dell'apparecchiatura sperimentale e di conseguenza ad annichilarsi. Nel 2011, sempre al CERN di Ginevra, i ricercatori dell'esperimento ALPHA (Antihydrogen Laser PHysics Apparatus) hanno sintetizzato e intrappolato 38 atomi di anti-idrogeno per un tempo di 172 millisecondi a una temperatura inferiore a 0.5 kelvin. Il tempo di confinamento e la temperatura ottenuti al CERN hanno permesso per la prima volta di studiare lo spettro atomico dell'anti-idrogeno. Sempre nel 2011, nei Brookhaven National Laboratory sono stati prodotti ed analizzati alcuni nuclei di anti-elio, cioè antiparticelle alfa. E la ricerca continua, perchè l'antimateria è probabilmente la più inaspettata e la più brillante delle scoperte di Paul Dirac.

Naturalmente il modello di Dirac del mare di elettroni presenta un grosso problema: se esso contiene infiniti elettroni, la sua massa totale è infinita. Dunque, in base alla Relatività Generale di Einstein, il vuoto avrebbe una massa tale da curvare lo spazio, e da curvarlo così tanto da ridurlo... ad un punto geometrico! Siccome nessuno ha mai osservato il collasso dell'universo, significa che quello di Dirac in realtà è un modello, utile per capire la formazione e l'annichilazione di coppie elettrone-positrone, ma scarsamente realistico. L'Elettrodinamica Quantistica (QED), introdotta negli anni '50 da Richard P. Feynman (1918-1988), che prevede la quantizzazione del campo elettromagnetico, riesce a descrivere la creazione di antiparticelle mediante artifici formali, indipendentemente dal modello pelagico di Dirac. La stessa teoria riesce a tappare i buchi del Modello Atomico Quanto-Relativistico, come lo spostamento di Lamb, fenomeno di spostamento dei livelli energetici dell'atomo di sodio che neppure l'equazione di Dirac era riuscita ad interpretare. chi vuole sapere di più sulla QED, consulti questa pagina di un altro mio ipertesto.
Aggiungiamo una scoperta recentissima, che dobbiamo a un team composto da ricercatori del Politecnico di Milano, dell'Istituto Nazionale di Fisica Nucleare, dell'Università degli Studi di Milano, del Centro Albert Einstein (AEC) per la Fisica Fondamentale e del Laboratorio di Fisica delle Alte Energie (LHEP) dell'Università di Berna. Il 3 maggio 2019 essi hanno annunciato di essere riusciti a dimostrare che anche il positrone ha una doppia natura di onda e particella, osservando per la prima volta l'interferenza di onde di antimateria formate da singoli positroni con la doppia fenditura in una versione aggiornata dell'esperienza di Young. Ciò conferma che le leggi della meccanica quantistica valgono anche per l'antimateria. « Il successo di questo nostro esperimento apre la strada dell'interferometria quantistica per sistemi con antimateria », ha spiegato Marco Giammarchi, ricercatore della sezione INFN di Milano e responsabile della collaborazione QUPLAS (Quantum interferometry with Positrons and LASers) che ha realizzato l'esperimento. Ora l'obiettivo a lungo termine dell'esperimento è utilizzare la straordinaria accuratezza dell'interferometria per misurare l'interazione gravitazionale materia-antimateria.
.
9.5 Le simmetrie e il Teorema CPT
Adesso abbiamo un quadro abbastanza completo di come vanno le cose negli atomi e dintorni. Prima però di chiudere questo ipertesto dedicato ai misteri della Meccanica Quantistica, vogliamo introdurre alcuni concetti fondamentali, senza i quali è impossibile comprendere appieno non solo la logica della Fisica Atomica, Molecolare e dello Stato Solido, ma anche quella alla base della Fisica del Nucleo e delle Particelle. Anche in questo caso la farà da padrone il formalismo dell'Analisi Matematica, per cui quel che segue è riservato a chi possiede conoscenze universitarie.
Le funzioni d'onda quantistiche, infatti, sono dotate di simmetria rispetto all'inversione spaziale. Tale operazione consiste nel cambiare segno alle variabili spaziali:
r → – r
Costruiamo l'operatore corrispondente a questa trasformazione. Si tratta di una mera operazione geometrica, non di una grandezza fisica, ma se riteniamo la simmetria una proprietà delle particelle esattamente come la posizione o la quantità di moto, nessuno vieta di ripetere per essa i ragionamenti della Meccanica degli Operatori. In tale formulazione della Meccanica Quantistica, se un operatore commuta con l'hamiltoniano, si può dimostrare che esso corrisponderà ad una costante del moto. In altre parole, anche gli operatori di grandezze senza corrispondente dinamico possono avere un significato dinamico!
Definiamo allora l'operatore P, tale che:
![]()
L'operatore P si dice operatore parità. Applichiamolo all'equazione di Schrödinger per gli stati stazionari (6.8), o all'equazione di Dirac per gli stati stazionari (9.11), ed avremo:
Applichiamo ora i due operatori in ordine inverso:
Sostituendo – r a r in Ĥ, si trova:

Dunque, se nell'equazione:
![]()
cambiamo r con – r, si ha:
![]()
e di conseguenza la (9.14) ci dà:
Confrontando tra loro la (9.13) e la (9.15) si ha:
![]()
Di conseguenza, H e P commutano tra di loro.

Paul Ehrenfest, suo figlio Paul junior ed Albert Einstein
Ora, nella Meccanica degli Operatori vale il cosiddetto Teorema di Ehrenfest, il quale prende il nome dallo sfortunato matematico austriaco Paul Ehrenfest (1880-1933), suicidatosi il 25 settembre 1933 perchè affetto da depressione. Secondo questo teorema, l'evoluzione dei valori medi di ogni osservabile fisica descritta dalla Meccanica Quantistica coincide con l'evoluzione descritta dalla Meccanica Classica. Applicando alla precedente il Teorema di Ehrenfest si scopre che:

Ma P non dipende esplicitamente dal tempo, per cui dP / dt = 0. Conclusione: la parità si conserva nel tempo. In altre parole. l'evoluzione di tutte le particelle è tale che la loro funzione d'onda conserva la simmetria rispetto all'inversione delle coordinate spaziali. In ogni stato i valori medi della parità sono gli autovalori; proviamo dunque a trovarli. L'equazione agli autovalori della parità è:
![]()
Applico ora l'operatore P ad entrambi i membri:
![]()
Ma l'operatore P è involutivo: se lo applico due volte, ritorno alla funzione di partenza. Dunque:
![]()
da cui p2 = 1, cioè p = ± 1. Ne segue che sono possibili solo due casi:

Le funzioni d'onda che soddisfano la prima delle precedenti sono pari, quelle che soddisfano la seconda sono dispari. Una funzione, in generale, non è né pari né dispari rispetto all'inversione delle coordinate; le ψ(r) invece devono necessariamente esserlo. Ciò dipende dal fatto che il campo è centrale, ed ha un'importanza notevole. Infatti tale assunto permette ad esempio di dimostrare che una transizione elettronica da uno stato ad un altro può avvenire solo se la parità della ψ cambia.
Oltre alla parità, però, c'è un'altra operazione della medesima importanza cui le ψ obbediscono: è l'operazione che ad una particella fa corrispondere la sua antiparticella, invertendo il segno della sua carica elettrica:
q → – q
Tale operazione prende il nome di coniugazione di carica, perchè il corrispondente operatore Ĉ trasforma una funzione d'onda (che in generale è una funzione complessa) nella sua coniugata, che in Meccanica degli Operatori si indica con il simbolo ψ*. Quest'operatore è involutivo come P, ed è privo di corrispondente non relativistico, cioè esiste solo nel modello di Dirac

Anche a Ĉ si associa un'equazione agli autovalori:
![]()
Non è difficile verificare che, poiché in Ĥ compare e2, Ĉ ed Ĥ commutano tra loro. Si può dunque ripetere lo stesso discorso appena fatto per l'operatore parità; applicando Ĉ a sinistra ad entrambi i membri della precedente, si trova:
![]()
Dunque, c = ± 1. Questo si esprime dicendo che, così come ho solo due stati di parità, pari o dispari, posso avere solo due stati di carica:
![]()
e tutte le funzioni d'onda quanto-relativistiche obbediscono a questa proprietà.
Infine, è possibile introdurre un terzo operatore, quello di inversione rispetto al tempo:
t → – t
in modo che:
![]()
Lascio al lettore volenteroso il compito di verificare che anche l'operatore T commuta con l'hamiltoniano, e che una qualunque funzione d'onda può essere solo pari o dispari rispetto all'inversione temporale:

Perchè abbiamo introdotto questi tre operatori? Perchè nella descrizione relativistica delle particelle elementari è necessaria l'invarianza della trasformazione composta CPT. Questo è noto con il nome di Teorema CPT, e fu formulato nel 1954 da Julian Schwinger (1918-1994), Gerhart Lüders (1920-1995) e Wolfgang Pauli (1900-1958). Nella Fisica delle Particelle risulta molto importante la scoperta che questo teorema può essere violato. Infatti, a proposito di quanto detto su materia ed antimateria, se il Teorema CPT fosse sempre verificato, nell'universo noi dovremmo avere tanta materia quanta antimateria. Ma se così fosse, nei primi istanti di vita del cosmo tutte le antiparticelle si sarebbero annichilate con le corrispondenti particelle, e l'universo come lo vediamo oggi non sarebbe mai nato. Il fatto è che ben presto si accumularono gli indizi di una possibile violazione della simmetria CPT. Già nel 1956 i fisici teorici cinesi Tsung-Dao Lee (李政道, 1926-) e Chen Ning Yang (楊振寧, 1922-) dell'Università di Chicago, allievi di Enrico Fermi, proposero che la parità non dovesse essere conservata in caso di decadimento dovuto alla Forza Nucleare Debole, e nel 1957 la loro collega Wu Chien Shiung (吳健雄, 1912-1997) dimostrò che il cobalto-60 ha una direzione privilegiata in cui emette elettroni quando va incontro a decadimento beta, osservando questa violazione della conservazione della parità. Anche con la violazione della parità si pensava che la combinazione di coniugazione di carica e parità avrebbe lasciato il sistema invariante: si parla a tal proposito di invarianza CP. Tuttavia nel 1964 James Watson Cronin (1931-2016) e Val Logsdon Fitch (1923-2015) dell'Università della California a Berkeley dimostrarono con uno straordinario esperimento che esisteva una piccola violazione dell'invarianza CP nel decadimento del mesone K o kaone; chi vuol saperne di più, consulti questa pagina. Il fatto che questi fenomeni violino il Teorema CPT ci dice che la produzione di particelle e di antiparticelle può essere asimmetrica.
Il sospetto è ormai diventato quasi certezza il 21 marzo 2019, quando è stato annunciato che l'esperimento LHCb presso il Large Hadron Collider del CERN di Ginevra ha dimostrato per la prima volta come le particelle contenenti un quark charm si comportano in modo leggermente diverso dalle loro rispettive antiparticelle quando decadono. Questa differenza si manifesta in particolare nelle particelle chiamate mesoni D0 con la violazione della simmetria CP. L'entità della violazione, hanno sottolineato con cautela i ricercatori, è ancora insufficiente per spiegare l'asimmetria tra materia e antimateria che si osserva in natura, ma il risultato conferma che si è sulla buona strada per cercare nuovi processi di violazione di CP non solo nelle particelle contenenti il quark charm, ma anche per altri tipi di quark. Proprio grazie a fenomeni come questo, all'inizio del tempo, circa un elettrone su un miliardo e un protone su un miliardo riuscirono a scampare alla reciproca annichilazione con le rispettive antiparticelle, e furono proprio queste particelle superstiti a dare vita al cosmo, alle galassie, alle stelle, all'uomo. E anche a Paul Dirac, senza il quale tutto questo non sarebbe mai stato neppure sognato!

Wu Chien Shiung con Wolfgang Pauli
.
9.6 Appendice: le quasiparticelle
In questa appendice, ultimissimo paragrafo del presente libro, vorrei illustrarvi cosa sono le cosiddette quasiparticelle. Con questo nome si indicano gli strani fenomeni che si verificano quando un sistema microscopico complicato come un solido si comporta come se contenesse particelle debolmente interagenti nello spazio libero. Per l'esattezza queste particelle fantomatiche, che "non esistono ma è come se esistessero", sono tipicamente chiamate quasiparticelle se sono correlate ai fermioni ed eccitazioni collettive se sono correlate ai bosoni, sebbene la distinzione precisa tra i due casi non sia universalmente accettata da tutti. Ad esempio, mentre un elettrone viaggia attraverso un semiconduttore, il suo movimento è disturbato in modo veramente complicato dalle sue interazioni con tutti gli altri elettroni e nuclei; tuttavia si comporta approssimativamente come un elettrone con una massa diversa (detta massa efficace) che viaggia imperturbato nello spazio libero. Questo "elettrone con una massa diversa" è chiamato "quasiparticella di elettroni". Un altro esempio di quasiparticella lo abbiamo già visto nel § 8.3: il moto collettivo degli elettroni nella banda di valenza di un semiconduttore è lo stesso che si avrebbe se il materiale contenesse invece quasiparticelle a carica positiva denominate lacune. Esempi di eccitazioni collettive sono invece i fononi, che descrivono la quantizzazione delle vibrazioni atomiche in un solido, e i plasmoni, derivati da oscillazioni del plasma. Il concetto di quasiparticella è molto importante nella Fisica dello Stato Solido poiché è uno dei pochi modi conosciuti di semplificare la versione quantistica del problema dei molti corpi.
L'idea delle quasiparticelle fu lanciata per la prima volta dal fisico sovietico Lev Davidovic Landau (1908-1968) per studiare l'elio-3 liquido. Per sistemi come questo, infatti, la dinamica delle molecole è definita da un'equazione cinetica del campo medio, vagamente simile alle equazioni della Teoria Cinetica dei Gas. Un'equazione simile, l'equazione di Vlasov, ideata nel 1938 da Anatoly Alexandrovic Vlasov (1908-1975), è valida per un plasma nell'approssimazione in cui le particelle cariche si considerano in movimento nel campo elettromagnetico generato collettivamente da tutte le altre particelle, e le collisioni ad alta energia tra le particelle cariche vengono trascurate perchè giudicate improbabili. Il concetto di fonone fu invece introdotto nel 1932 dal fisico sovietico Igor Yevgenyevic Tamm (1895-1971), che coniò il termine in analogia con "fotone", e da allora il loro numero è andato crescendo a velocità impressionante.
In pratica, le quasiparticelle sono uno strumento matematico per semplificare la descrizione dello Stato Solido. Mentre è possibile avere una singola particella (elettrone, protone, neutrone...) fluttuante nello spazio, una quasiparticella può esistere solo all'interno di sistemi a molte particelle interagenti, principalmente solidi. Il movimento in un solido è estremamente complesso: per via della legge di Coulomb, ogni elettrone e protone viene spinto e attratto da tutti gli altri elettroni e protoni nel solido, che possono essere essi stessi in movimento. Sono queste forti interazioni che rendono molto difficile prevedere e comprendere il comportamento dello Stato Solido. D'altra parte, il movimento di una particella classica non interagente è relativamente semplice; si muoverà in linea retta a velocità costante. Sulla base di questa filosofia, il movimento complicato delle particelle reali in un solido può essere trasformato matematicamente nel moto molto più semplice di quasiparticelle immaginarie, che si comportano piuttosto come particelle non interagenti.
Proviamo ad entrare nel dettaglio. Qualsiasi sistema, non importa quanto complicato, ha uno stato fondamentale ed una serie infinita di stati eccitati ad alta energia. Tuttavia è praticamente impossibile descrivere direttamente ogni particella in un sistema macroscopico dato che, tanto per fare un esempio, un granello di sabbia appena visibile ad occhio nudo (diciamo di 0,1 mm di diametro) contiene circa 1017 nuclei e 1018 elettroni. Ognuno di questi attrae o respinge tutti gli altri sulla base della legge di Coulomb. In linea di principio, l'equazione di Schrödinger (6.4) prevede esattamente come si comporterà questo sistema; ma l'equazione di Schrödinger in questo caso è un'equazione differenziale alle derivate parziali in uno spazio vettoriale con 3 × 1018 dimensioni (una dimensione per ogni coordinata x, y, z di ciascuna particella)! Cercare di risolvere una tale equazione è umanamente impossibile, sia alle quadrature che con metodi numerici, esattamente come in un altro mio ipertesto abbiamo visto che non si può risolvere le equazioni del moto per tutte le 1023 molecole di un gas, e bisogna invece ricorrere agli strumenti della Fisica Statistica e della Teoria Cinetica dei Gas.
Per semplificare il problema possiamo tenere conto del fatto che, in molti contesti, solo gli stati eccitati inferiori, con energia ragionevolmente vicina a quella dello stato fondamentale, sono rilevanti per noi. Ciò a causa della distribuzione di Boltzmann, la quale ci porta a ritenere improbabile che si verifichino fluttuazioni termiche molto alte ad una data temperatura. Studiando le proprietà delle singole quasiparticelle è dunque possibile ottenere una grande quantità di informazioni sui sistemi a bassa energia, ad esempio riguardo la capacità termica. In quest'ultimo caso, infatti, un cristallo può immagazzinare energia formando fononi, e/o formando eccitoni, e/o formando plasmoni, eccetera, ed ognuna di queste quasiparticelle fornisce un contributo separato alla capacità termica complessiva.
Quasiparticelle ed eccitazioni collettive sono un tipo di stato eccitato a bassa energia. Ad esempio, un cristallo allo zero assoluto si trova nello stato fondamentale, ma se il cristallo è fatto vibrare leggermente a una frequenza particolare, cioè se aggiungiamo ad esso un fonone, esso si trova invece in uno stato eccitato di bassa energia. Il singolo fonone è chiamato un'eccitazione elementare. Più in generale, gli stati eccitati a bassa energia possono contenere un numero qualsiasi di eccitazioni elementari: per esempio molti fononi, insieme ad altre quasiparticelle e ad eccitazioni collettive. Quando il materiale è caratterizzato da diverse eccitazioni elementari, esse possono coesistere simultaneamente e indipendentemente tra loro? No, questo non è mai esattamente vero. Ad esempio, un solido con due fononi identici non ha esattamente il doppio dell'energia di eccitazione di un solido con un solo fonone, perché la vibrazione del cristallo è leggermente anarmonica. Tuttavia, in molti materiali le eccitazioni elementari sono molto vicine all'essere indipendenti le une dalle altre. Pertanto, come punto di partenza, vengono trattate come entità indipendenti; le eventuali correzioni a tale descrizione semplificata sono incluse a loro volta tra le eccitazioni elementari, come "scattering fonone-fonone". Pertanto, utilizzando quasiparticelle o eccitazioni collettive, invece di analizzare tutte le 1018 particelle in gioco, è necessario trattare solo una manciata di eccitazioni elementari in larga misura indipendenti tra di loro. Si tratta quindi di un approccio molto efficace per semplificare il problema a molti corpi nella Meccanica Quantistica. Questo approccio tuttavia non è utile per tutti i sistemi: in materiali fortemente correlati, le eccitazioni elementari sono così lontane dall'essere indipendenti che questa metodologia non è nemmeno utile come punto di partenza. Comunque ogni tipo di equazione cinetica di campo medio, in cui si ha che fare con un numero sterminato di particelle, e ognuna di esse si muove nel campo medio generato da tutte le altre, implica l'introduzione di una nuova quasiparticella o di una nuova eccitazione collettiva.
C'è una differenza nel modo in cui quasiparticelle ed eccitazioni collettive vengono intuitivamente immaginate. Solitamente una quasiparticella viene considerata come una « particella rivestita » (in inglese "dressed particle"), cioè costruita attorno a una particella reale, detta « particella nuda » (in inglese "bare particle"), circondata da un campo quantistico che è fisicamente inseparabile da essa; in pratica, il comportamento della "particella rivestita" è influenzato fortemente dall'ambiente ad esso circostante. Un tipico esempio di ciò è l'"elettrone rivestito", cioè un elettrone che include la dinamica caotica dei fotoni e delle coppie di elettroni e positroni che circondano l'elettrone originale nell'Elettrodinamica Quantistica; oppure i polaritoni, quasiparticelle introdotte nella Fisica dello Stato Solido, rivestite di eccitazioni dipolari in un mezzo saturo di fotoni. Invece un'eccitazione collettiva viene solitamente immaginata come un riflesso del comportamento aggregato del sistema, senza una singola particella reale al suo interno. Un esempio tipico di tale eccitazione collettiva è il fonone, che caratterizza il movimento vibratorio di ogni atomo nel cristallo.
Tuttavia, queste due visualizzazioni lasciano qualche ambiguità. Per esempio, un "magnone" in un solido ferromagnetico può essere descritto in due modi perfettamente equivalenti: come un difetto mobile (uno spin diretto in maniera apparentemente errata) in un perfetto allineamento di momenti magnetici, oppure come un quanto di un'onda di rotazione collettiva, il che implica la precessione di molti spin. Nel primo caso, il magnone è concepito come una quasiparticella, nel secondo caso come un'eccitazione collettiva. Tuttavia, entrambe quelle riferite sono descrizioni equivalenti e corrette. Come mostra questo esempio, la distinzione intuitiva tra una quasiparticella e un'eccitazione collettiva non è particolarmente importante o fondamentale per la sua comprensione; tuttavia, ha sollevato parecchi problemi nell'ambito della filosofia della scienza, in particolare in relazione alla questione se queste entità fisiche debbano o meno essere considerate "reali".

Lev Davidovic Landau (1908-1968)
Detto questo, ora vedremo alcuni significativi esempi di quasiparticelle e di eccitazioni collettive, in rigoroso ordine alfabetico.
Angolone. Può essere utilizzato per descrivere la rotazione delle molecole nei solventi. Postulato teoricamente per la prima volta nel 2015, l'esistenza dell'angolone è stata confermata il 27 febbraio 2017 da Mikhail Lemeshko dell'Istituto Austriaco di Scienza e Tecnologia, dopo una serie di esperimenti che duravano da vent'anni. Lemeshko ha scoperto infatti che le molecole pesanti e leggere ruotano all'interno di goccioline di elio superfluido in accordo con la teoria dell'angolone.
Anyone o qualunquone. È un tipo di quasiparticella che esiste in sistemi bidimensionali ed è la generalizzazione del concetto di fermione e bosone; infatti lo scambio di due particelle di questo tipo può portare a una variazione della fase globale ma non coinvolge le osservabili del sistema. Gli anyoni possono dividersi in abeliani e non abeliani: i primi sono stati rivelati e ricoprono un ruolo importante nell'effetto Hall quantistico frazionario, scoperto nel 1982 da Daniel Chee Tsui (1939-) e Horst Ludwig Störmer (1949-), mentre i secondi non sono ancora stati trovati con certezza nonostante vi sia un'area di ricerca molto attiva in questo settore, giacché potrebbero portare alla realizzazione del cosiddetto computer quantistico topologico. Nel 2005 un gruppo di fisici della Stony Brook University a New York costruì un interferometro quasiparticellare e rivelò frange di interferenza di anyoni. Con lo sviluppo delle tecnologie a semiconduttori è stato possibile realizzare la deposizione di strati sottili bidimensionali (come il grafene), perciò in futuro si potrà indagare il possibile utilizzo degli anyoni in ambito elettronico.
Eccitone. Questo bosone descrive
lo stato eccitato di un sistema della materia condensata. In un isolante o in un
semiconduttore può essere visto come uno stato legato di un elettrone e di una
lacuna, interagenti mediante la forza di Coulomb. L'eccitone presenta molte
analogie con l'atomo di idrogeno: il protone dell'atomo di idrogeno è sostituito
dalla lacuna nell'eccitone. La complicazione rispetto all'atomo di idrogeno
risulta dal fatto che nell'eccitone i costituenti elementari si muovono
non nel
vuoto, ma nel mezzo costituito da tutti gli altri elettroni del sistema, e
questi schermano l'interazione attrattiva fra l'elettrone e la lacuna. Il
risultato è un'energia di legame molto più piccola e una dimensione molto
maggiore rispetto all'atomo di idrogeno. Ulteriore effetto è giocato dalla massa
efficace dei costituenti immersi nel materiale, in generale diversa dalla massa
nuda dell'elettrone. La formazione di un eccitone può essere provocata
dall'assorbimento di un fotone: un elettrone viene così eccitato dalla banda di
valenza a quella di conduzione, lasciando una lacuna di carica positiva nella
banda di valenza, alla quale è attratto per mezzo della forza di Coulomb. L'eccitone
risulta dal legame tra l'elettrone e la sua lacuna; questo comporta che l'eccitone
abbia un'energia leggermente minore rispetto alla coppia non correlata
elettrone-lacuna. La funzione d'onda e le energie degli eccitoni possono essere
calcolate risolvendo la cosiddetta Equazione di Bethe-Salpeter, che permette di
calcolare ad esempio lo spettro di assorbimento ottico. Nel 2018 un gruppo di
fisici guidato da Peter Abbamonte, dell'Università
dell'Illinois a Urbana-Champaign, ha osservato sperimentalmente un nuovo
stato della materia composto da eccitoni, e per questo denominato
eccitonio.
Previsto per via teorica negli anni sessanta ma mai scoperto prima, l'eccitonio
e stato osservato misurando le eccitazioni collettive delle coppie
elettrone-lacuna in un materiale portato a 190 K (– 83 °C). Secondo un'altra
ricerca effettuata dal gruppo di Tobias Heindel della
Technischen
Universität di Berlino, un particolare tipo di eccitone può essere usato
 anche come
qubit. Si tratta dell'eccitone oscuro, una coppia in cui elettrone e
lacuna hanno lo stesso spin e quindi non possono ricombinarsi emettendo
direttamente un fotone (da cui il termine oscuro). Per questo ha una vita
relativamente più lunga dell'eccitone chiaro.
anche come
qubit. Si tratta dell'eccitone oscuro, una coppia in cui elettrone e
lacuna hanno lo stesso spin e quindi non possono ricombinarsi emettendo
direttamente un fotone (da cui il termine oscuro). Per questo ha una vita
relativamente più lunga dell'eccitone chiaro.
Fasone. Questa quasiparticella esiste nei quasicristalli, un particolare tipo di solido quasiperiodico, nel quale cioè gli atomi sono disposti in una struttura deterministica ma non ripetitiva, cioè non periodica come avviene invece nei normali cristalli (vedi la figura accanto, che ricorda un quadro di Escher). Vennero osservati per la prima volta nel 1984 da Dan Shechtman (1941-) dell'Israel Institute of Technology, scoperta per la quale gli è stato assegnato il Premio Nobel per la chimica nel 2011. Simile al fonone, il fasone è associato con il moto atomico, ma mentre i fononi sono correlati alla traslazione degli atomi, i fasoni sono associati ai riordinamenti atomici. Da queste nuove disposizioni risultano onde che descrivono la posizione degli atomi nel cristallo in fase di mutamento, e da qui deriva il termine "fasone". La teoria idrodinamica dei quasicristalli prevede che la loro tensione (fonone) si attenui rapidamente. Diversamente, il rilassamento della tensione del fasone è diffusivo ed è molto più lento. Pertanto, i quasicristalli metastabili cresciuti tramite il rapido raffreddamento della fusione mostrano la tensione del fasone associata agli spostamenti e agli ampliamenti dei raggi X e ai picchi di diffrazione elettronica.
Fonone. Si tratta di un'eccitazione collettiva associata alla vibrazione degli atomi in una struttura cristallina rigida; in pratica, è un quanto di onda sonora in un cristallo. Esso gioca un ruolo importante nella comprensione di molte proprietà dei solidi, come il calore specifico, la conduzione termica, la conduzione elettrica e la propagazione del suono; lo stesso nome del fonone deriva dal greco φωνή, "suono". Anche la spiegazione microscopica della superconduttività si basa sull'interazione tra fononi ed elettroni, che danno vita alle cosiddette coppie di Cooper. Il fonone è la controparte quantistica di quello che in meccanica classica è noto come sviluppo in modi normali, ossia la scomposizione delle vibrazioni in "vibrazioni elementari", dette per l'appunto modi normali. Tutte le vibrazioni possono essere viste e descritte formalmente come una sovrapposizione dei modi normali. Le vibrazioni elementari da un punto di vista classico sono delle onde, ma si è visto che nella Meccanica Quantistica vige il cosiddetto dualismo onda-particella, e dunque anche i fononi si possono trattare con proprietà particellari. La manifestazione più evidente di tale comportamento particellare è data dallo scattering Brillouin e Raman, in cui l'interazione tra fotoni e fononi viene matematicamente descritta come un semplice processo d'urto. Nel novembre 2013 sono stati brevettati i primi diodi acustici e termici basati sullo studio e la manipolazione dei fononi. Inoltre, e recentissima la scoperta che i fononi trasportano anche una piccola quantità di massa: è la sorprendente conclusione a cui è giunto Alberto Nicolis, ricercatore della Columbia University di New York, analizzando il comportamento delle onde sonore in moto attraverso l'elio superfluido. Egli ha dimostrato che in questo particolare mezzo di propagazione i fononi nel loro moto possono interagire con un campo gravitazionale e trasportare una massa. In seguito l'italiano Angelo Esposito, dello stesso ateneo, con alcuni colleghi ha esteso l'analisi considerando mezzi di propagazione ordinari, come i liquidi e i solidi, trovando gli stessi risultati: i fononi trasportano una piccola -massa gravitazionale. L'aspetto più sorprendente della cosa sta nel fatto che l'origine di questa massa è interamente classica, cioè non è un effetto quantistico né relativistico. Finora era sfuggita perché di solito la propagazione delle onde sonore è studiata con modelli lineari semplificati, utili per la maggior parte degli scopi ma insufficienti a rilevare l'esistenza della loro piccola massa. Non solo: l'analisi mostra che la massa trasportata dai fononi sarebbe in realtà negativa. I fononi quindi, nella loro propagazione, cadrebbero... verso l'alto, in modo simile a un oggetto che galleggia verso la superficie dell'acqua. Gli scienziati ammettono di non aver ancora compreso completamente il significato fisico del fenomeno, specie nei solidi, ma sottolineano la possibilità di osservare questo effetto sperimentalmente, per esempio considerando onde sonore in moto attraverso atomi ultrafreddi o addirittura (obiettivo più ambizioso) quelle generate nei terremoti.

Modello di fonone nell'ossido di zinco (da questo sito)
Istantone. È una soluzione classica delle equazioni del moto con una quantità di moto finita e non nulla, nella teoria dei campi quantistici; più precisamente, è una soluzione delle equazioni del moto della teoria classica dei campi su uno spazio-tempo euclideo. In tali teorie quantistiche, le soluzioni delle equazioni del moto possono essere pensate come massimi locali della quantità di moto, minimi locali o punti di sella. Gli istantoni sono importanti nella teoria dei campi quantistici perché appaiono come le correzioni quantistiche principali al comportamento classico di un sistema, e possono essere usati per studiare l'effetto tunnel in vari sistemi come la teoria di Yang-Mills. Si ritiene che la condensazione degli istantoni sia la spiegazione della fase caotica indotta dal rumore nota come criticità auto-organizzata.
Lacuna. Come visto parlando dei semiconduttori, è una quasiparticella che consiste nella mancanza di un elettrone in uno stato quantico, ed ha la carica opposta di un elettrone. Per questa quasiparticella vi rimando al § 8.3.
Magnone. È un'eccitazione collettiva associata alla struttura di spin degli elettroni in un reticolo cristallino. È il quanto di un'onda di spin, cioè di una perturbazione della configurazione di spin di stato fondamentale del sistema. Come qualsiasi altra eccitazione, il magnone porta energia e momento, ed è un bosone; può inoltre decadere in altri due magnoni la cui energia non è maggiore di quella del magnone originale. I magnoni possono essere rivelati sperimentalmente attraverso esperimenti di diffusione anelastica di neutroni. Il concetto di magnone fu introdotto nel 1930 da Felix Bloch (1905-1983) per spiegare la riduzione di magnetizzazione spontanea in una sostanza ferromagnetica. Una teoria più precisa delle onde di spin quantizzate o magnoni fu sviluppata nel 1940 da Ted Holstein (1915-1985) ed Henry Primakoff (1914-1987) e successivamente nel 1956 da Freeman Dyson (1923-). La prima osservazione sperimentale diretta di magnoni è dovuta al canadese Bertram Brockhouse (1918-2003), che nel 1957 li rivelò grazie ad un esperimento di diffusione anelastica di neutroni nella ferrite.
Monopolo magnetico. Previsto in un lavoro teorico del 1931 da Paul Dirac, ha rappresentato una sorta di Santo Graal della fisica fin dall'elaborazione della teoria elettromagnetica, negli ultimi decenni dell'Ottocento, a causa di un'evidente asimmetria tra fenomeni elettrici e fenomeni magnetici. Mentre le cariche elettriche si possono separare, ottenendo i monopoli elettrici (corpi con una carica definita, positiva o negativa), è impossibile fare lo stesso con i poli magnetici, indicati convenzionalmente come "nord" e "sud". Se prendiamo un magnete, in esso è possibile individuare un polo sud e un polo nord, ma questi poli non si possono separare: se si spezza in due il magnete, si ottengono due magneti più piccoli, ciascuno dei quali dotato di un polo sud e un polo nord. In altri termini, sembrava impossibile isolare un monopolo magnetico. Invece nel 2013 gli equivalenti di monopoli magnetici sono stati riprodotti sperimentalmente da David Hall, dell'Amherst College, in Massachusetts, in un gas di atomi di rubidio mantenuto a una temperatura vicina allo zero assoluto. Il monopolo magnetico inoltre si presenta nei sistemi di materia condensata come il ghiaccio di spin, una sostanza che non ha un singolo stato di minima energia; tipici esempi sono i cristalli di titanite, che trasportano una carica magnetica efficace, oltre ad essere dotati di altre proprietà tipiche delle quasiparticelle come una massa efficace.
Plasmone. È un'eccitazione collettiva che rappresenta il quanto delle oscillazioni di un plasma, in cui tutti gli elettroni oscillano simultaneamente rispetto a tutti gli ioni. Il plasmone è associato ad una oscillazione longitudinale del campo elettromagnetico. Invece il plasmone di superficie è un plasmone localizzato in prossimità della superficie di un solido. È caratterizzato da un'energia differente e da una relazione di dispersione (relazione tra lunghezza d'onda ed energia) che va come la radice quadrata del momento.
Polaritone o quasiparticella fotonica. È un fotone influenzato dalle sue interazioni con il materiale che attraversa. In particolare, la quasiparticella fotonica ha una relazione di dispersione modificata rispetto a quella nel vuoto, come viene descritto dall'indice di rifrazione del materiale. Nel 2006 all'École Polytechnique de l'Université de Lausanne per la prima volta è stato creato un condensato di Bose-Einstein di polaritoni alla temperatura di 19 K; sono in corso esperimenti per raggiungere tale condizione a temperatura ambiente. Ricordiamo che il condensato di Bose-Einstein è un fenomeno quantistico a catena che porta la maggior parte delle particelle bosoniche di un sistema in uno stesso stato finale, a partire da differenti stati iniziali. Tale stato esotico della materia è strettamente collegato a fenomeni come la superconduttività e la superfluidità. Nel dicembre 2012 al California Institute of Technology di Pasadena è stato annunciato che attraverso polaritoni plasmonici di superficie che concentrano la luce in uno spazio ristretto si potrà memorizzare una quantità di dati pari a 50 TeraByte per pollice quadrato, un'enormità. É stato inoltre scoperto che un fluido di polaritoni in rotazione ha proprietà simili a quelle di un buco nero rotante, e ciò apre ad interessanti sviluppi in campo astrofisico.
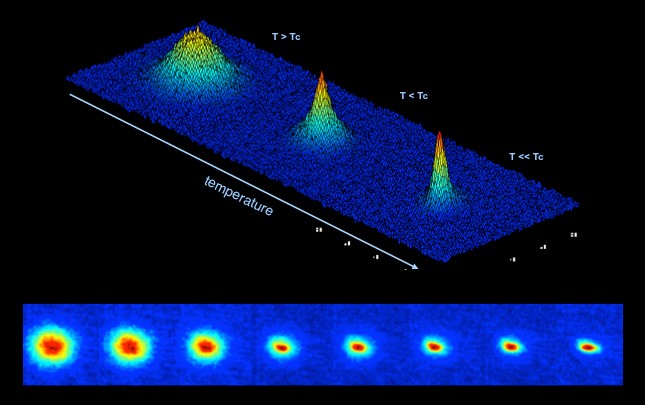
La formazione di un condensato di Bose-Einstein (foto NASA)
Polarone. Da non confondersi con il polaritone, è una quasiparticella che si forma quando un elettrone interagisce con la polarizzazione degli ioni ad esso circostanti. Un elettrone che si muove in un cristallo interagendo con gli ioni sarà permanentemente circondato da una regione di polarizzazione del reticolo, causata dalla deformazione del reticolo degli ioni. L'elettrone attira verso di sé gli ioni caricati positivamente; muovendosi attraverso il cristallo, l'elettrone porta con sé la distorsione del reticolo, sicché è possibile parlare di una nuvola di fononi che accompagna l'elettrone. Un polarone è un fermione e si forma quando una carica in una catena molecolare influenza la geometria locale dei nuclei, causando un'attenuazione o persino un'inversione delle ampiezze dei legami vicini. Il concetto di polarone è usato riguardo ai modi di rendere un polimero un conduttore elettrico, come ad esempio il poliparafenilenevinilene, un diffuso polimero conduttore disponibile commercialmente. In questo caso si è provato a creare uno stato eccitato che in seguito si diseccita emettendo luce oppure tramite vibrazioni. Uno dei modi più semplici per creare questo stato eccitato è alternare la geometria dei legami, drogando il polimero. Un liquido di polaroni è stato osservato in perovskiti cuprate drogate, che mostrano superconduttività ad alta temperatura critica. I polaroni sono stati resi famosi dal franchise di Star Trek perchè Harry Kim, un ufficiale a bordo dell'astronave USS Voyager, svegliandosi in una realtà alternativa, crea una distorsione nel continuum spaziotemporale con un raggio di polaroni. « In Star Trek amavano prendere i nomi di vere quasiparticelle e attribuire loro proprietà magiche », ha commentato Douglas Natelson, fisico della Rice University in Texas, studioso proprio delle quasiparticelle.
Quasiparticella di Bogolyubov. Come detto nel § 8.7, la superconduttività viene trasportata dalle coppie di Cooper, solitamente descritte come coppie di elettroni che si muovono attraverso il reticolo cristallino praticamente senza incontrare resistenza. Una coppia di Cooper rotta è chiamata quasiparticella di Bogolyubov, dal nome del suo scopritore, Nikolaj Nikolajevic Bogolyubov (1909–1992). Si differenzia dalla quasiparticella convenzionale nei metalli perché combina le proprietà di un elettrone caricato negativamente e di una lacuna con carica positiva; gli oggetti fisici come gli atomi di impurità, dai quali le quasiparticelle si diffondono in un metallo comune, influenzano solo debolmente l'energia di una coppia di Cooper in un superconduttore convenzionale. Nei superconduttori convenzionali, l'interferenza tra le quasiparticelle di Bogoliubov è difficile da vedere ma, a causa delle loro complesse strutture elettroniche globali, sono ben visibili nei superconduttori cuprati ad alta temperatura.
Quasiparticella di Landau. Si tratta di un elettrone dentro un solido, influenzato da altre forze e interazioni all'interno del solido stesso. La quasiparticella di Landau ha la stessa carica e lo stesso spin di un elettrone "normale" (la particella elementare nota con questo nome), e sotto molti altri aspetti, specialmente nei metalli in condizioni normali, assomiglia molto all'elettrone a noi familiare. Tuttavia, la sua massa può differire significativamente da quella di un normale elettrone; anche il campo elettrico viene modificato, come risultato dell'interazione con il campo elettrico globale dentro il solido.
Quasiparticella di Laughlin o fermione composito. Essa prende il nome dall'americano Robert Betts Laughlin (1950-) e compare in un sistema bidimensionale soggetto a un grande campo magnetico, come ad esempio in quei sistemi che mostrano l'effetto Hall quantistico frazionario. Queste quasiparticelle differiscono dalle particelle comuni in due modi. Innanzitutto, la loro carica può essere inferiore alla carica elettronica; e infatti nel 1999 un esperimento basato sull'effetto tunnel ha mostrato che esistono effettivamente delle quasiparticelle con carica e/3 ed e/5, dovute alla corrente di Hall quantistica che si crea in un gas di elettroni bidimensionale. In secondo luogo possono essere un tipo particolare di anyoni, e quindi non sarebbero né fermioni né bosoni.
Rotone. È un'eccitazione collettiva associata alla rotazione di un superfluido come l'elio-3. È un quanto di vortice. La relazione di dispersione delle eccitazioni elementari nel superfluido mostra dapprima un incremento lineare dell'energia con il momento che raggiunge un massimo, seguito infine da un minimo. Le eccitazioni nella regione lineare sono chiamate fononi, mentre quelle intorno al minimo sono chiamate rotoni. Le eccitazioni vicino al massimo sono da alcuni chiamate maxoni. Un caso particolare è lo skyrmione, osservato sperimentalmente in sistemi di materia condensata, che può formare sottili pellicole magnetiche.

L'onda Soliton immaginata nel telefilm "Star Trek, The Next Generation"
Solitone. È un'onda solitaria auto-rinforzante causata dalla concomitanza, con cancellazione reciproca, tra effetti non lineari e dispersivi in un mezzo di propagazione. Si riscontra in molti fenomeni fisici, dato che emerge come soluzione di una vasta classe di equazioni differenziali alle derivate parziali non lineari che descrivono molti fenomeni. Il solitone fu descritto per la prima volta dall'ingegnere navale scozzese John Scott Russell (1808-1882), che nel 1834 osservò un'onda solitaria risalire la corrente nell'Union Canal in Scozia per chilometri senza perdere energia. Russell riprodusse il fenomeno in un recipiente di onde, e lo chiamò "Onda di Traslazione". Tra i primi a scoprire la presenza di solitoni nell'oceano fu Alfred Richard Osborne (1942-) nel 1980 nel Mare delle Andamane, e successivamente furono scoperti in altri mari. Esistono anche dei solitoni atmosferici, come il fenomeno del Morning Glory Cloud in Australia, dove solitoni di pressione viaggianti in un piano di inversione di temperatura producono vaste nubi cilindriche. I solitoni sono studiati anche in meccanica quantistica, grazie al fatto che potrebbero fornirne una nuova fondazione attraverso il percorso incompiuto di de Broglie, conosciuto come "Teoria della doppia soluzione" o "Meccanica delle onde non lineare", sviluppata nel 1927 e ripresa negli anni '50. L'uso dei solitoni fu proposto nel 1973 da Akira Hasegawa (1934-), dei laboratori Bell di AT&T, per migliorare il rendimento delle trasmissioni nelle reti ottiche di telecomunicazioni con effetti anti-dispersivi. Nel 1988 Linn Mollenauer e la sua squadra trasmisero solitoni a più di 4.000 km usando l'effetto Raman dal nome del suo scopritore, l'indiano Chandrasekhara Venkata Raman (1888-1970). Nel 1991, sempre nei laboratori Bell, un'équipe trasmise dei solitoni a più di 14.000 km utilizzando amplificatori di erbio. Nel 2001 i solitoni incontrarono un'applicazione pratica con la prima apparecchiatura di telecomunicazioni che li utilizzava per il trasporto di traffico di segnali reali in una rete commerciale. I solitoni sono diventati così popolari da diventare persino protagonisti di una puntata del telefilm "Star Trek, The Next Generation", intitolata appunto "L'onda Soliton", in cui si immagina che possano spingere delle astronavi fino ad una velocità assai maggiore di quella della luce.
Spinone. È la quasiparticella prodotta come risultato della separazione spin-carica dell'elettrone. Gli elettroni, essendo di carica uguale, si respingono; di conseguenza, al fine di attraversare tutti insieme un ambiente estremamente affollato, sono costretti a modificare il loro comportamento. Una ricerca, pubblicata nel luglio del 2009 dall'Università di Cambridge e da quella di Birmingham, ha dimostrato che gli elettroni possono saltare dalla superficie del metallo su un filo quantico strettamente localizzato per mezzo dell'effetto tunnell, e così facendo possono separarsi in due quasiparticelle, definite dai ricercatori spinoni e oloni. Gli spinoni possono formare un liquido di spin quantistico in alcuni minerali come l'Herbertsmithite con struttura chimica ZnCu3(OH)6Cl2, scoperto per la prima volta nel 1972 in Cile, che prende il nome dal mineralogista Herbert Smith (1872-1953).
Topolaritone o polaritone topologico. È una quasiparticella descritta per la prima volta nel 2015 da Gil Refael del Caltech di Pasadena, che risulta dall'unione di un fotone e di un eccitone, e quindi è per metà luce e per metà materia. Studiato nell'ambito dei cosiddetti isolanti topologici, una classe di materiali ottenuti accoppiando strati di silicio semiconduttore a strati di bismuto, ha la particolarità di non possedere il fenomeno della riflessione all'indietro, cosicché usando queste particelle si potrebbe trasportare fotoni in un'unica direzione. Il dispositivo per generare topolaritoni potrebbe essere implementato nei sistemi di uso comune: per esempio nei semiconduttori o in strati di spessore atomico di composti con metalli di transizione, già usati per realizzare guide d'onda e microcavità.
Trione. Identificata nel 2015 da Abdelaziz Boulesbaa del Department of Energy allo Oak Ridge National Laboratory, è stata osservata in uno strato sottilissimo di materiale semiconduttore, 100.000 volte più sottile di un capello umano! In particolare si trattava di uno strato di disulfuro di tungsteno bidimensionale eccitato da un fascio laser. Quando un semiconduttore assorbe la luce laser, l'eccitazione provocata dalla luce crea un eccitone. Il trione negativo si osserva quando un eccitone si lega, a sua volta, a un elettrone, mentre se un eccitone si lega a una lacuna si ha un trione positivo. Per osservare i trioni, gli scienziati hanno messo a punto un fascio di luce laser in grado di registrare filmati all'altissima risoluzione temporale di 40 femtosecondi (4 x 10–14 s). La scoperta potrà rivelarsi utile per lo sviluppo di nuove tecnologie nel campo dell'optoelettronica, dello sfruttamento dell'energia solare e dell'informatica quantistica.
.
E anche stavolta, abbiamo concluso l'ultimo capitolo; vi ringrazio molto per avermi seguito fin qui, nonostante l'oggettiva difficoltà degli argomenti trattati. Mi piace concludere con le parole del Premio Nobel per la Fisica 2017 Kip Thorne (1940-), padre della ricerca delle onde gravitazionali:
« Noi viviamo in un universo governato da leggi fisiche che noi uomini siamo in grado di scoprire, decifrare, imparare in profondità e usare per controllare il nostro destino. Anche senza l'aiuto di intelligenze extraterrestri, siamo in grado di affrontare quasi ogni catastrofe che l'universo può scatenarci contro, così come quelle provocate da noi stessi, dal cambiamento climatico ai disastri biologici e nucleari. Per far questo, per controllare il nostro destino, è però necessario che una larga parte della popolazione comprenda e apprezzi la scienza. Il suo modo di operare. Ciò che ci insegna in merito all'universo, alla Terra e alla vita. I risultati che può raggiungere. Quali sono i suoi limiti dovuti alle inadeguatezze della conoscenza o della tecnologia. In che modo questi limiti possono essere superati. Come possiamo passare dalle semplici congetture alle ipotesi fondate e quindi alla verità. Quanto siano rare - ma molto importanti - le rivoluzioni in cui la nostra percezione della verità viene a cambiare. »
Spero che anche il mio testo dedicato alla Meccanica Quantistica possa contribuire alla comprensione di tutto ciò! Tuttavia, alcuni di voi mi faranno notare che l'argomento non è concluso: dopo la Meccanica Quantistica, la Fisica Atomica, la Fisica Molecolare, la Fisica dello Stato Solido, molti vorrebbero leggere lezioni di Fisica Nucleare, Fisica delle Particelle, Astrofisica, Cosmologia, e persino delle attuali frontiere della Fisica al di là del Modello Standard. Proprio per venire incontro alle richieste in tal senso di alcuni di voi, ho scritto un nuovo libro, dedicato proprio a tali ardui argomenti che la scuola e l'università italiane di oggi tendono ampiamente a sorvolare. Chi vuole inoltrarsi in questo territorio inesplorato, clicchi qui e parta con me per un nuovo, straordinario viaggio, fino alle estreme frontiere della attuale conoscenza umana!!

"Le Frontiere della Fisica", opera della mia studentessa Nives Vecchio (5 C a.s. 2018/19)
A questo punto, se vi sentite pronti a misurarvi con alcuni esercizi conclusivi, cliccate qui. Per tornare all'indice, infine, il link è questo. Grazie a tutti per l'attenzione!
