

|
"La strada per la conoscenza delle stelle conduce all'atomo; e l'importante conoscenza dell'atomo è stata raggiunta attraverso le stelle." Arthur Eddington (1882–1944) |
.
3.1 I limiti di Rutherford
Il modello di atomo proposto da Rutherford presentava delle evidenti difficoltà. Infatti in esso gli elettroni dovevano muoversi lungo orbite circolari (per maggior precisione, ellittiche), per cui gli elettroni risultano accelerati, perchè soggetti all'accelerazione centripeta. Ora, come ci dice l'elettrodinamica classica, fondata sulle Equazioni di Maxwell, una carica accelerata irraggia, disperdendo nello spazio tutta la propria energia. Gli elettroni dovrebbero perciò precipitare a spirale sul nucleo. In quanto tempo?
Eseguiamo allo scopo un bilancio tra la forza centripeta e la forza di attrazione coulombiana, si ha:

essendo me la massa dell'elettrone, Z e la carica del nucleo ed e quella dell'elettrone (si sono trascurati i segni). Da qui si ricava:

Ora, ( me R v ) è il modulo del momento angolare L dell'elettrone, una delle costanti del moto, per cui:

e quindi:

L'accelerazione centripeta avvertita dall'elettrone è allora pari a:

L'elettrodinamica classica ci dice che la potenza irraggiata da una carica accelerata è data dalla cosiddetta formula di Larmor:

Ora, l'energia cinetica perduta dall'elettrone è:

E quindi, il tempo necessario per irradiare tutta questa energia è pari a:


Introducendo i valori delle costanti, si può stimare:

Dunque la vita media dell'atomo di Rutherford è appena di qualche decimiliardesimo di secondo! Le sole leggi della Fisica Classica, insomma, non erano assolutamente sufficienti a giustificare il modello planetario, nonostante esso fosse stato convalidato dalle esperienze sullo scattering alfa.
.
3.2 Cenni di spettroscopia
A risolvere il problema fu il danese Niels Bohr (1885-1962), uno dei maggiori ingegni del secolo scorso, il quale intuì che un modello di questo genere poteva sostenersi solo grazie alla nuova Fisica ideata da Max Planck. Del resto, il modello di Rutherford (come quello di Thomson) non riusciva in alcun modo a rendere conto delle righe dello spettro di emissione dell'idrogeno e degli altri gas, mentre Niels Bohr appuntò la propria attenzione proprio su questi spettri. Urge perciò spendere due parole sulla scienza chiamata spettroscopia.

Niels Bohr su una banconota danese da 500 corone
Porta questo nome la scienza che si occupa dell'analisi degli spettri luminosi emessi dalle varie sostanze quando vengono eccitate, in genere riscaldandole ad alta temperatura. In particolare essa studia, in funzione della lunghezza d'onda, la distribuzione energetica delle onde elettromagnetiche emesse o assorbite dai costituenti della materia. Tale disciplina nacque quando Isaac Newton mise in evidenza la decomposizione della luce bianca nelle sue componenti monocromatiche per mezzo di un prisma trasparente, il cosiddetto fenomeno della dispersione cromatica; il termine "spettro" è stato coniato proprio da Newton. A partire dal 1830 la spettroscopia assurse al rango di scienza esatta, grazie ai tedeschi Robert Bunsen (1811-1899) e Gustav Robert Kirchhoff (1824 -1887), che lavorando insieme all'Università di Heidelberg costruirono il primo spettroscopio moderno, e si resero conto che gli spettri ottenuti dalla luce emessa dai vari elementi cambiavano da sostanza a sostanza, e nessun composto aveva uno spettro identico a quello di un altro; in pratica, dalla distribuzione delle cosiddette "righe spettrali" (o "righe di Fraunhofer"), scoperte nel 1814 da Joseph von Fraunhofer (1787-1826) nello spettro della luce solare, era possibile risalire alla composizione chimica di qualsiasi oggetto. Per questo l'analisi spettroscopica divenne in breve uno dei più validi sistemi di indagine per identificare e studiare le proprietà della materia. È vero che uno stesso elemento può emettere spettri distinti (alcune righe appaiono, altre scompaiono), ma ciò deriva dal grado e dalla modalità di eccitazione; ogni spettro di righe è sempre caratteristico dell'elemento in quelle determinate condizioni di eccitazione. Naturalmente noi studieremo lo spettro a righe dell'atomo di idrogeno, cioè l'atomo più semplice di tutti; non a caso, tale spettro è stato il primo a venire interpretato, e poi è servito da modello per descrivere e suddividere in serie le ben più complesse distribuzioni di righe negli spettri degli altri elementi.
Modello didattico di spettroscopio (cliccare per ingrandire)
Mediante l'analisi spettroscopica, Bunsen e Kirchhoff scoprirono due elementi fino ad allora sconosciuti, il rubidio e il cesio, e misero le basi della moderna astrofisica, deducendo dagli spettri delle stelle la loro composizione chimica (la prima stella diversa dal Sole del quale venne studiato lo spettro fu Vega, nel 1872). Inoltre fu proprio usando tecniche spettroscopiche che l'inglese Sir Joseph Norman Lockyer (1836-1920) e il francese Pierre Jules César Janssen (1824-1907), indipendentemente l'uno dall'altro nello stesso anno 1868, scoprirono nelle righe spettrali del Sole delle righe fino ad allora sconosciute, non appartenenti a nessun elemento tra quelli noti; compresero così di essere davanti ad un nuovo elemento, che fu chiamato elio (in greco "Sole"), ritenendo che esso esistesse solo nell'astro solare; in seguito lo scozzese Sir William Ramsay (1852-1916) lo identificò anche sulla Terra.
Se si osserva attraverso un prisma la luce emessa da una sostanza opportunamente eccitata (spesso scaldata fino a portarla allo stato aeriforme, si ottiene la formazione di uno spettro di emissione, che può essere di vari tipi:
a) spettro
continuo, formato da una successione continua di frequenze, dal rosso al
violetto nel visibile. Di solito viene e messo dai solidi e dai liquidi
riscaldati.
b) spettro a righe: è formato da una successione
discreta di righe che possono estendersi dall'infrarosso fino all'ultravioletto.
Questo vuol dire che l'elemento riscaldato non emette tutte le lunghezze d'onda
possibili in un dato intervallo, ma solo particolari lunghezze d'onda,
corrispondenti a particolari colori nella regione del visibile.
c) spettro a bande: è formato da una serie di
righe fittissime che si addensano intorno a certe lunghezze d'onda, in modo da
dar vita ad una serie di bande continue. Viene in genere emesso da gas formati
da molecole poliatomiche.

Noi ci occuperemo in particolare dello spettro a righe. Si noti che si può avere anche uno spettro di assorbimento: facendo passare un fascio di luce bianca attraverso una data sostanza, in genere attraverso un gas o dei vapori, nello spettro continuo appaiono delle righe scure trasversali, segno del fatto che la sostanza ha "assorbito" determinate frequenze. Tali sono le righe di Fraunhofer osservate nello spettro solare: la luce dell'astro attraversa i suoi strati più esterni, i cui componenti assorbono parte di tale luce. Oggi sappiamo ad esempio che le righe catalogate da Fraunhofer come A e B (le meglio visibili) sono dovute all'ossigeno, la riga C all'idrogeno (quella che oggi viene chiamata Hα), le righe D1 e D2 al sodio e la D3 all'elio. Confrontando gli spettri di emissione e di assorbimento di una medesima sostanza, nel 1859 Gustav Kirchhoff si accorse che le righe scure di assorbimento corrispondono perfettamente alle righe chiare di emissione; in altre parole, ogni sostanza è in grado di assorbire quelle lunghezze d'onda che nelle stesse condizioni fisiche è capace di emettere. Questo è oggi noto come il Principio di Inversione dello Spettro.
A questo punto, però, sorge un problema. Le righe spettrali emesse dagli atomi di un dato elemento presentano una successione di righe, e quindi di lunghezze d'onda, che apparentemente appaiono distribuite senza alcuna regolarità. Perchè dunque certi elementi emettono solo particolari lunghezze d'onda, e non altre? Qual è il meccanismo, per così dire intrinseco, in base al quale il sodio emette solo luce di lunghezza d'onda tipica del colore giallo, e non, ad esempio, del colore verde? Per tutto il XIX secolo, tale domanda rimase senza risposta, a causa della nostra ignoranza circa la struttura intima della materia. Un primo, timido passo lo fece nel 1885 il fisico svizzero Johann Jakob Balmer (1825-1898), insegnante in un liceo svizzero, il quale con pazienza certosina cercò una possibile regolarità nella distribuzione di tali lunghezze d'onda nello spettro di emissione dell'idrogeno, ed elaborò la formula seguente, passata alla storia appunto come formula di Balmer:
In essa, RH è una costante determinata sperimentalmente dallo svedese Johannes Robert Rydberg (1854-1919), e detta per questo Costante di Rydberg, ed n è un numero intero maggiore di 2. Al variare di n, si trovano le frequenze di quelle che vengono solitamente chiamate le righe della "serie di Balmer", cioè quelle nella regione della luce visibile. Da notare che si tratta di una legge empirica, cioè dedotta dall'analisi dei dati sperimentali, non per via teorica da altre già consolidate leggi fisiche. Il valore più attendibile della costante di Rydberg, trovato attraverso numerosissime misurazioni successive, è:
RH = 1,097 x 107 m–1
In seguito altri epigoni di Balmer trovarono formule analoghe per esprimere le righe spettrali dell'idrogeno nelle regioni dell'infrarosso e dell'ultravioletto: Theodore Lyman (1874-1954) nel 1906 elaborò una legge che esprimeva la regolarità delle righe spettrali ultraviolette emesse dall'idrogeno attraversato da una corrente elettrica, mentre il tedesco Friedrich Paschen (1865-1947) nel 1908, l'americano Frederick Brackett (1896-1988) nel 1922, l'americano August Herman Pfund (1879-1949) nel 1924 e l'americano Curtis Judson Humphreys (1898-1986) nel 1953 ne scoprirono altrettante nell'infrarosso, via via sempre più lontano. Per queste righe nel 1908 si scoprì che vale il cosiddetto principio di combinazione di Ritz, dal nome del fisico svizzero Walther Ritz (1878-1909): la differenza tra gli inversi delle lunghezze d'onda di due righe di una data serie fornisce l'inverso della lunghezza d'onda di una riga di un'altra serie spettrale. Rydberg allora generalizzò come segue la (3.1):
Ccon m < n. Se in essa si pone:
m = 1 ed n = 2, 3, 4, 5... si ottiene la serie di Lyman;
m = 2 ed n = 3, 4, 5, 6... si ottiene la serie di Balmer;
m = 3 ed n = 4, 5, 6, 7... si ottiene la serie di Paschen;
m = 4 ed n = 5, 6, 7, 8... si ottiene la serie di Brackett;
m = 5 ed n = 6, 7, 8, 9... si ottiene la serie di Pfund;
m = 6 ed n = 7, 8, 9, 10... si ottiene la serie di Humphreys;
e così via (le serie per valori superiori di m sono senza nome e difficilissime da osservare). In pratica, tutte le lunghezze d'onda delle righe spettrali dell'idrogeno si possono esprimere attraverso la differenza di due termini, detti termini spettrali, di cui il primo è costante del tipo RH / m2, ed il secondo è variabile del tipo RH / n2. Per elementi diversi dall'idrogeno, la (3.2) mantiene la sua validità, anche se cambia il valore della costante RH. Il problema principale sollevato dalle formule (3.1) e (3.2) consiste nel fatto che esse, trovate per tentativi, a lungo rimasero solo delle leggi empiriche, cioè un procedimento mnemonico per ricavare le righe spettrali dell'idrogeno, e non si aveva idea di come giustificarle da un punto di vista teorico. Inoltre, esse ponevano un grosso problema di natura fisica: se lo spettro è caratteristico di ogni elemento, come lo è la formula di Balmer, allora gli atomi sono tutti uguali tra di loro, mentre il modello planetario lascia ampia libertà ai singoli atomi, dal momento che gli elettroni possono apparentemente orbitare sulle orbite che preferiscono. Per risolvere quest'apparente contraddizione, Niels Bohr sviluppò una sua teoria atomica tenendo conto delle intuizioni di Planck, che oggi ci appare geniale nella sua semplicità, e fu grazie ad essa che la formula di Balmer acquistò un significato fisico.
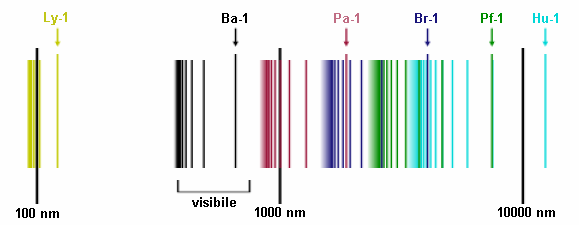
Le diverse serie nelle righe spettrali dell'idrogeno
3.3 Bohr quantizza le orbite
Allo scopo, Bohr ipotizzò la quantizzazione delle orbite elettroniche; in altre parole, secondo lui l'elettrone in orbita intorno al nucleo non perde energia solo perchè ruota su alcune particolari traiettorie, caratterizzate da precisi valori discreti di energia, all'interno delle quali esso non irraggia. Bohr chiamò tali orbite livelli o stati stazionari. La quantizzazione delle orbite ideata da Bohr si può esprimere affermando che il momento angolare L dell'elettrone è un multiplo intero di quella che viene chiamata la costante di Planck ridotta o costante di Dirac:

In simboli, dunque:

Ma L = m v r, per cui:
Per semplificarci la vita, supporremo le orbite elettroniche circolari. L'elettrone allora si mantiene su tale orbita perchè la forza centripeta è controbilanciata dalla forza elettrostatica esercitata dal nucleo (che ha carica + e, essendo per l'idrogeno Z = 1):

da cui:

Ricavo v dalla (3.3) e la sostituisco nella precedente, scrivendo:

E da qui ottengo:
Dunque la quantizzazione del momento angolare espressa dalla (3.3) implica la quantizzazione dei raggi delle orbite; ma implica anche quella della energia E degli stati stazionari di Bohr. Infatti tale energia è pari alla somma dell'energia cinetica e dell'energia potenziale dell'elettrone:

e per la (3.4):

Otteniamo così:
Introduco ora la lunghezza d'onda Compton ridotta dell'elettrone:

la cosiddetta costante di struttura fine:

e l'energia a riposo dell'elettrone:

Le suddette quantizzazioni possano allora scriversi:

Introduciamo le due grandezze seguenti e sostituiamo i valori numerici delle costanti:

Le leggi di quantizzazione vengono perciò riscritte:

Se n = 1 ho r1 = a0 ed E1 = E0. Ne segue che a0 ed E0 sono il raggio, detto raggio di Bohr, e l'energia del primo livello quantizzato, detto livello fondamentale, dell'atomo di idrogeno. Peraltro, "livello fondamentale" è la traduzione di un termine inglese divenuto tristemente famoso dopo l'11 settembre 2001: "ground zero". Il fatto che E < 0 indica che l'elettrone non è libero, ma è legato all'atomo. I raggi e le energie delle orbite di Bohr si ricavano dalle formule seguenti:
Qui sotto ho rappresentato i valori di energia dei primi cinque livelli energetici dell'atomo di idrogeno. Come si vede, al crescere di n cresce anche l'energia, e l'elettrone si allontana progressivamente dal nucleo; infatti, l'elettrone è tanto meno legato all'atomo quanto più è lontano dal nucleo. n viene chiamato il numero quantico principale, e i livelli energetici con n = 1, 2, 3, 4, 5, 6, 7 per ragioni storiche sono indicati rispettivamente con le lettere maiuscole K, L, M, N, O, P, Q. L'energia dell'elettrone nella prima orbita di Bohr è detta energia di prima ionizzazione, perchè è quella necessaria per spostare l'elettrone dalla prima orbita di Bohr fino all'infinito, cioè praticamente fuori dall'atomo, e un atomo privato di un elettrone si dice ionizzato. Affermare che il livello K dell'atomo d'idrogeno ha energia pari a – 13,6 eV significa insomma affermare che occorrono 13,6 eV (cioè 2,166 x 10–18 J) per ionizzarlo, ovvero per prendere un elettrone posto su tale livello e portarlo fuori dal raggio d'azione del nucleo. Il livello L (con n = 2) avrà energia pari a – 13,5 / 4 = – 3,4 eV, e questa sarà l'energia di seconda ionizzazione, cioè occorreranno 3,4 eV (pari a 5,415 x 10–19 J) per portare un elettrone dal livello L all'infinito. Il livello M (con n = 3) avrà energia – 13,5 / 9 = – 1,5 eV, il livello N (con n = 4) avrà energia – 13,5 / 16 = – 0,85 eV, e così via. Questi livelli energetici vengono chiamati anche gusci, in inglese shell, da cui il nome di "modello atomico a shell" assegnato all'atomo di Bohr. K rappresenta la prima shell, cioè lo stato fondamentale: se l'atomo di idrogeno non è eccitato, l'elettrone si trova in questo stato.

Se però è eccitato, l'energia dell'elettrone cresce, ed esso letteralmente salta su di un livello energetico più elevato. Infatti, a differenza di quanto accade nel modello di Rutherford, dove l'elettrone può assumere valori qualsiasi di energia, nel modello a shell l'energia dell'elettrone può assumere solo i valori discreti dati dalla seconda delle (3.6), e quindi raggiunge inevitabilmente un altro dei livelli di Bohr. L'energia assorbita è pari alla differenza tra le energie dei due livelli, quello di partenza e quello di arrivo.
Però l'elettrone non può rimanere a lungo su questo stato eccitato: ben presto si diseccita, emettendo un fotone di frequenza f la cui energia h f è pari esattamente alla differenza di energia tra le due orbite:
![]()
Siano ora n il numero quantico principale dello stato eccitato ed m quello dello stato di partenza. Per la (3.5) sarà:

Passiamo ora dalle frequenze alle lunghezze d'onda, ottenendo:
con n > m. Calcoliamo il valore numerico della costante moltiplicativa:

Si osserva subito che essa è in ottimo accordo con il valore ottenuto sperimentalmente della costante di Rydberg RH! La precedente dunque coincide con la formula (3.2) che consente di ricavare le righe degli spettri. Bohr ha ottenuto un risultato incredibile, riuscendo a giustificare con un ragionamento teorico i risultati sperimentali ottenuti dalla spettroscopia nel secolo precedente, e per di più con un procedimento semplice quanto elegante, dal quale è immediato dedurre le serie spettroscopiche. In pratica, come si vede qui sotto, la serie di Lyman è generata dalle diseccitazioni elettroniche verso lo stato fondamentale K con m = 1; quella di Balmer è generata dalle diseccitazioni verso lo stato L con m = 2; quella di Paschen dalle diseccitazioni verso lo stato M con m = 3; e così via.

Se n → ∞, evidentemente l'elettrone sale al livello di energia E∞ = 0 J, cioè abbandona l'atomo, che viene così ionizzato.
Si osservi che, tra tutte le frequenze riportate nell'immagine soprastante, solo cinque valori, tutti appartenenti alla serie di Balmer, ricadono nella luce visibile. I cinque valori ricavabili dalla (3.1) e compresi entro questo spettro sono Hα = 656 nm, Hβ = 486 nm, Hγ = 434 nm, Hδ = 410 nm ed Hε = 397 nm; la H sta per idrogeno, e le lettere greche progressive α, β, γ, δ, ε corrispondono ai valori 1, 2, 3, 4, 5 di n. Come si vede nella figura sottostante, la riga detta Hα, che corrisponde alla transizione da n = 3 ad m = 2, emette luce rossa ed è una delle più frequenti nell'universo a causa dell'abbondanza in esso dell'idrogeno: è estremamente brillante in moltissimi oggetti astronomici, e contribuisce a conferire loro un colore tendente al rosso. La riga Hβ (da n = 4 ad m = 2) ricade invece nel verde, le righe Hγ (da n = 5 ad m = 2), Hδ (da n = 6 ad m = 2) ed Hε (da n = 7 ad m = 2) nel violetto, come si vede qui sotto. Le righe oltre quest'ultima transizione invece ricadono nella banda ultravioletta dello spettro.

A temperature ordinarie si osserva solo la serie di Lyman, perchè negli atomi di idrogeno è occupato solo lo stato a più bassa energia (quello con n = 1). Negli spettri stellari, invece, si osserva anche la presenza della serie di Balmer, perchè secondo la Termodinamica classica almeno un atomo su 108 sul Sole si trova nello stato eccitato con n = 2. Peraltro, proprio a questo modello di interpretazione degli spettri è legata la motivazione del Premio Nobel per la Fisica 2023. Perchè?
La spiegazione è semplice: i francesi Pierre Agostini (1941-) e Anne L'Huillier (1958-) e l'ungherese Ferenc Krausz (1962-) sono stati premiati, come si legge nella motivazione ufficiale, per aver messo a punto « metodi sperimentali che generano impulsi di luce dell’ordine dell'attosecondo per lo studio della dinamica degli elettroni nella materia ». E l'attosecondo è pari a un miliardesimo di miliardesimo di secondo: un tempo incredibilmente piccolo, se si pensa che un secondo contiene un numero di attosecondi pari al numero di secondi trascorsi da quando è nato l’universo!! Ma cosa c'entra questa scala di tempi così piccola? Ebbene, all’interno di una molecola gli atomi possono muoversi in tempi dell’ordine del femtosecondo, pari a un milionesimo di miliardesimo di secondo, una scala temporale piccolissima, ma già alla portata degli impulsi più brevi che possono essere prodotti tramite un laser. Grazie alla luce laser, quindi, è oggi possibile studiare con sufficiente livello di dettaglio i moti atomici e molecolari. Il discorso però è diverso se, anziché il moto degli atomi, si considera quello degli elettroni: le loro posizioni ed energie dentro gli atomi descritte qui sopra variano infatti in tempi compresi tra qualche unità e le centinaia di attosecondi, quindi anche 1000 volte inferiori ai tempi scala atomici e molecolari. Ora, il femtosecondo è stato considerato a lungo un limite sperimentale difficilmente superabile: anche migliorando le tecnologie esistenti basate sui laser, gli scienziati del settore non riuscivano a osservare la cosiddetta attofisica, cioè la dinamica degli elettroni alle scale temporali degli attosecondi. Ed è proprio qui che entrano in gioco i tre premiati con il Nobel 2023. Anne L’Huillier, oggi docente all’Università di Lund, nel 1987 (quando lavorava nei laboratori dell’Università di Parigi-Saclay) scoprì che, trasmettendo un fascio di luce laser a infrarossi attraverso un gas nobile, si otteneva un gran numero di onde elettromagnetiche di frequenza superiore rispetto alla frequenza fondamentale della luce laser, a cui si sovrappongono. L’Huillier capì che le armoniche ulteriori sono prodotte dall’interazione della luce laser con gli atomi del gas, che fornisce ad alcuni elettroni un’energia in eccesso, poi emessa sotto forma di luce. Fu presto chiaro che l’interazione tra queste armoniche ulteriori, nelle giuste condizioni, avrebbe potuto produrre una serie di impulsi di luce ultravioletta di durata pari ad alcune centinaia di attosecondi. Tuttavia, solo nel 2001 Pierre Agostini (oggi all’Ohio University) sviluppò una tecnica sperimentale nota come “metodo RABBIT”, in grado di generare impulsi di luce consecutivi della durata di appena 250 attosecondi. Al 1996 risale il contributo di un gruppo di ricerca dell'università in cui io mi sono laureato, il Politecnico di Milano, di cui facevano parte Mauro Nisoli, Sandro De Silvestri e Orazio Svelto (1936-). I tre italiani hanno ideato una tecnica particolare di compressione ottica, poi applicata al laser usato dal gruppo di ricerca di Ferenc Krausz all’Università Tecnica di Vienna, e hanno stabilito il record di durata per quell’epoca di un impulso di luce, pari a 4,5 femtosecondi. Negli anni successivi il fisico ungherese ha perfezionato la tecnica, basandosi sul lavoro di L’Huillier, finché nel 2001 riuscì a generare i primi impulsi isolati di 650 attosecondi. Abbattere il muro dell’attosecondo ha rappresentato un passaggio cruciale per la comprensione dei fenomeni governati dai moti degli elettroni, aprendo la strada anche a numerose potenziali applicazioni che riguardano lo studio dei materiali e la cosiddetta "attochimica", dove l’obiettivo è sfruttare impulsi di luce ultrabrevi per indurre nelle molecole reazioni chimiche che non potrebbero avvenire naturalmente. Insomma, un Premio Nobel strameritato! (tra l'altro Krausz e L’Huillier nel 2022 avevano già ricevuto il prestigioso premio Wolf con la stessa motivazione)

Pierre Agostini, Ferenc Klausz e Anne L'Hullier
Quanto detto fin qui è valido anche per i cosiddetti atomi idrogenoidi, cioè quelli aventi un solo elettrone: si tratta degli ioni He+, Li2+, Be3+, eccetera. L'unica differenza sta nel fatto che la carica nucleare non è più + e, bensì + Z e, per cui la costante di Rydberg diventa pari a RZ = Z2 RH. Ad esempio, nel 1896 l'astronomo britannico Alfred Fowler (1868-1940) individuò nell'atomo di elio quella che da lui prende il nome di serie di Fowler, studiando lo spettro della stella Zeta Puppis:
![]()
e successivamente venne individuata la serie di Pickering, che prende il nome dal grande astronomo americano Edward Charles Pickering (1846-1919), scopritore della prima stella binaria spettroscopica:
![]()
che si può scrivere:
![]()
Dunque una riga ogni due della serie di Balmer dell'idrogeno corrisponde alla serie di Pickering! Al crescere di Z, però, le righe raggiungono rapidamente le frequenze tipiche dei raggi X; si parla allora di spettroscopia X. La spettroscopia X e γ è molto difficile da realizzare perchè questi raggi vengono assorbiti dall'atmosfera terrestre e non raggiungono la superficie: gli strumenti utilizzati per rilevare i raggi X e γ devono essere portati a grandi altezze usando palloni, razzi-sonda e satelliti. La prima sorgente di raggi X cosmici fu scoperta nel 1962 e fu battezzata Scorpius X-1 perchè si trova nella costellazione dello Scorpione. Il 23 luglio 1999 lo Space Shuttle Columbia portò in orbita il Chandra X-ray Observatory della NASA per l'osservazione del cielo nei raggi X, che prende il nome dal fisico indiano Subrahmanyan Chandrasekhar (1910-1995). Proprio per le scoperte compiute attraverso l'astronomia dei raggi X nel 2002 l'italiano Riccardo Giacconi (1931-) vinse il Premio Nobel per la Fisica. La spettroscopia a raggi X è oggi considerata una delle nuove frontiere dell'astronomia.
L'osservatorio spaziale a raggi X Chandra
.
3.4 L'esperienza di Franck e Hertz
Quanto abbiamo detto finora si basa su un'ipotesi, fatta da Niels Bohr, che non sembra giustificata da alcun riscontro sperimentale: l'esistenza di livelli energetici quantizzati nell'atomo d'idrogeno. Occorreva dunque un esperimento in grado di dimostrare effettivamente l'esistenza di tali livelli. A riuscirci per primi furono i tedeschi James Franck (1882-1964) e Gustav Ludwig Hertz (1887-1975), nipote dello scopritore delle onde hertziane, attraverso la selettività dell'assorbimento energetico da parte dei costituenti della materia. L'energia in questo caso veniva fornita agli atomi attraverso collisioni con elettroni, e gli atomi assorbivano solo quelle frazioni di energia che corrispondevano alle loro energie di eccitazione.

Franck ed Hertz usarono allo scopo un tubo elettronico simile ad un triodo termoionico. Per evitare che, nella zona tra la griglia G e la placca anodica P, avvenissero interazioni tra gli elettroni emessi dal filamento F e le molecole del riempimento gassoso, la pressione interna del gas venne scelta in modo che il cammino libero medio delle particelle catodiche, cioè la distanza media tra due urti consecutivi degli elettroni contro le molecole del gas, sia maggiore della distanza tra G e P. Questi elettrodi, molto vicini tra loro, sono collegati al generatore G1 in modo che, mantenendo costante durante l'esperienza la loro d.d.p., il potenziale di griglia rimanga sempre lievemente più elevato di quello di placca.
Sia Vg la d.d.p. tra F e G. Gli elettroni attraversano la griglia con energia ( e Vg ) e, se non avvengono fenomeni, essi avranno energia sufficiente per vincere il controcampo esistente tra griglia e placca anodica; si origina così una corrente IP misurata da un opportuno milliamperometro. Ricordando il funzionamento delle valvole termoioniche, la corrente di placca IP dovrebbe aumentare fino alla saturazione; invece, si osserva che la corrente dapprima cresce e poi, raggiunto un certo valore V1, si ha una brusca diminuzione della corrente. Quando il potenziale di griglia aumenta oltre V1, gli elettroni, dopo il primo urto anelastico, vengono nuovamente accelerati senza perdita di energia, in modo da raggiungere la placca P originando un'ulteriore aumento della corrente di placca. Ciò avviene fino al valore V2, quando si produce un nuovo urto anelastico con nuova caduta di corrente, e così via, come mostra il diagramma sottostante.

Indichiamo con E1, E2, E3... le energie corrispondenti agli stati stazionari degli atomi del gas; finché l'energia e V degli elettroni è minore del primo valore di eccitazione ( E2 – E1 ), il sistema atomico non viene perturbato, e gli elettroni restano nello stato fondamentale. Quando l'energia e V acquista dalle particelle urtanti è maggiore o uguale ad ( E2 – E1 ), l'atomo, a seguito dell'assorbimento energetico, può essere condotto nel primo stato eccitato. Analogamente, si possono spiegare le altre brusche variazioni di corrente.
In definitiva, ogni qualvolta si produce un urto anelastico, cioè quando un atomo assorbe energia, le aliquote energetiche in gioco corrispondono, nell'ambito degli errori sperimentali, alle energie di eccitazione. Variando il gas nel triodo, variano i livelli energetici corrispondenti alle cadute di corrente anodica; per il resto, il fenomeno si presenta con le stesse modalità.
Il risultato più interessante dell'esperienza consiste nel fatto che, se si controlla con uno spettrometro la regione in cui avvengono le collisioni anelastiche, nello strumento appare una riga caratteristica dell'elemento in esame, allorché la corrente IP crolla. Ciò significa che l'atomo, portato in uno stato eccitato a seguito dell'interazione con gli elettroni, ritorna allo stato fondamentale riemettendo l'incremento energetico sotto forma di radiazioni elettromagnetiche di particolare frequenza. Queste ricerche nel 1925 valsero a Franck ed Hertz il Premio Nobel per la Fisica.
Gustav Ludwig Hertz (Amburgo, 22 luglio 1887 – Berlino, 30 ottobre 1975)
.
3.5 Gli atomi di Rydberg e la massa nucleare
Consideriamo un atomo in cui un elettrone è eccitato a un livello energetico molto, molto alto. Nello spazio interstellare esistono atomi i cui elettroni esterni si trovano in stati con numero quantico principale n fino a 350, che sono stati scoperti grazie all'impiego di tecniche radioastronomiche. In laboratorio invece si sono ottenuti e studiati atomi con n compreso tra 10 e 100. Un atomo in queste condizioni si chiama atomo di Rydberg e le sue dimensioni sono gigantesche: sono stati osservati atomi di Rydberg con diametri fino a 10–2 mm, cioè centomila volte più grandi del diametro di un atomo nello stato fondamentale! Inoltre, questi stati eccitati hanno vite medie assai lunghe. Mentre la vita media tipica per uno stato atomico eccitato più basso è dell'ordine di 10–8 s, vi sono atomi di Rydberg con vita media di un secondo. Come se non bastasse, gli atomi di Rydberg possono venire ionizzati gia da campi elettrici relativamente deboli.
Se l'elettrone esterno di un atomo viene eccitato a un livello energetico molto alto, entra in un orbitale che e molto al di fuori di quelli degli altri elettroni. In tali condizioni l'elettrone eccitato "vede" un nocciolo atomico, formato dal nucleo e da tutti gli elettroni interni, che ha carica + e, esattamente come la carica del nucleo di idrogeno. Finché l'elettrone eccitato non si avvicina troppo a questo nocciolo, si comporta come se appartenesse ad un atomo di idrogeno. Per questo gli atomi di Rydberg si comportano, sotto molti aspetti, come atomi di idrogeno. Mentre il raggio di un'orbita elettronica e proporzionale a n2, come ci dice la (3.4), la differenza tra le energie di due livelli consecutivi decresce come 1 / n3. Le insolite proprietà degli atomi di Rydberg sono legate proprio a queste potenze di n. Ad esempio, un atomo di Rydberg con n = 30 ha un raggio dell'ordine di 500 Ǻ, un'energia di legame dell'ordine di 10–2 eV e una vita media dell'ordine di 30 microsecondi.
In laboratorio si ottengono atomi di Rydberg eccitando gli atomi con luce laser. La loro presenza può essere rivelata con il campo elettrico che si ottiene tra le armature di un condensatore, facendo passare tra di esse un fascio di tali atomi. Piccoli campi elettrici, dell'ordine di poche centinaia di V / cm, sono in grado di ionizzare questi atomi; gli ioni possono poi essere rivelati con un moltiplicatore di elettroni. Quando un atomo di Rydberg passa a uno stato di energia immediatamente inferiore emettendo un fotone, la radiazione emessa è nel lontano infrarosso o nelle microonde, e fu proprio l'osservazione di questa radiazione che nel 1965 permise di dimostrare l'esistenza di atomi di Rydberg nello spazio interstellare (dove la densità degli atomi è così bassa che le collisioni sono assai rare). In tempi recenti nuovi laser a banda stretta hanno permesso di realizzare verifiche sperimentali sulle proprietà di atomi di Rydberg con numeri quantici grandissimi, per i quali in precedenza erano disponibili solo previsioni teoriche.

Johannes Robert Rydberg (Halmstad, 8 novembre 1854 – Lund, 28 dicembre 1919)
Ma non è tutto. I muoni possono formare i cosiddetti atomi muonici, osservati per la prima volta nel 1952, in cui un elettrone è sostituito da un muone (μ). Si tratta di una particella scoperta nel 1936 dall'americano Carl Anderson (1905-1991) che ha molte affinità con l'elettrone, ma una massa 207 volte maggiore di esso ed una vita media di soli 2,2 microsecondi. Per produrli si bombarda la materia con protoni molto energetici (almeno 440 MeV); prima di decadere, i muoni possono essere catturati in orbite atomiche esterne, al posto degli elettroni. Poiché i muoni si comportano come elettroni pesanti, è possibile ripetere per essi i calcoli relativi al modello di Bohr, ed allora il raggio delle orbite muoniche è dato dalla (3.4) in cui la massa me dell'elettrone è sostituita dalla massa m del muone:

Siccome mμ = 207 me, se ne deduce che i raggi delle orbite di Bohr degli atomi muonici sono più piccoli dei raggi delle corrispondenti orbite elettroniche di un fattore 207. Il muone è quindi molto più vicino al nucleo di quanto non sia l'elettrone, e gli atomi muonici sono estremamente piccoli, addirittura poco più grandi di un nucleo. I muoni restano più a lungo nelle immediate vicinanze del nucleo, e questa grande vicinanza tra la particella e la carica nucleare implica energie di legame e di eccitazione molto elevate. Come ci ha insegnato Niels Bohr, nell'effettuare transizioni verso orbite più interne, i muoni emettono radiazioni di frequenza corrispondente alla differenza di energia tra le due orbite; a differenza degli atomi ordinari, in cui queste frequenze si trovano nella regione spettrale della luce visibile o degli ultravioletti, per gli atomi muonici tali differenze ricadono nella regione dei raggi X. La presenza di atomi muonici dunque è rivelata da un'emissione di raggi X, la cui intensità si attenua progressivamente, con un tempo di dimezzamento pari a quello del muone. L'interesse per gli atomi muonici è giustificato dal fatto che in essi i muoni si avvicinano al nucleo assai più degli elettroni, il che rende possibile uno studio più approfondito del potenziale nucleare. Inoltre qualcuno spera di poter utilizzare gli atomi muonici per catalizzare la reazione di fusione nucleare.
E ora, prima di cambiare paragrafo, una postilla necessaria. Per quanto si ripetano con cura i calcoli numerici della costante moltiplicativa che appare nella formula di Balmer (3.2), si ottiene:

mentre il valore sperimentale di tale costante è pari a:
![]()
C'è un'ineliminabile differenza di 60 cm–1. Come interpretarla?
L'idea che ci viene in mente è che essa sia dovuta al moto nucleare. Infatti la massa del nucleo è grande, ma non certo infinita, per cui non è vero che l'elettrone ruota attorno al nucleo: entrambi ruotano attorno ad un centro di massa comune. Si può descrivere tale moto come se fosse quello di una particella fittizia avente una massa pari alla cosiddetta massa ridotta del sistema. Considerati infatti il nucleo e l'elettrone di massa rispettivamente mN ed me, per il Secondo Principio della Dinamica su di essi agiscono due forze pari a:
![]()
Ma il Terzo Principio della Dinamica (cioè il Principio di Azione e Reazione) ci dice che F12 = – F21, cioè che:
![]()
Da qui ricaviamo:
![]()
L'accelerazione relativa tra nucleo ed elettrone è perciò uguale a:
![]()
Quest'ultima si può riscrivere:

Di conseguenza il sistema elettrone-nucleo può essere sostituito con un'unica particella avente massa μ = F12 / a, e quindi pari a:
![]()
detta appunto la massa ridotta del sistema elettrone-nucleo. Allora nella (3.7) a me devo sostituire μ, ottenendo così:

e di conseguenza:

da cui:
![]()
Questa è una misura spettroscopica della massa del nucleo. Considerando atomi più pesanti di quello d'idrogeno, si osserva che il rapporto mN / me cresce rapidamente al crescere del numero atomico Z, e con essa decresce la correzione alla legge di Rydberg.
Arnold Sommerfeld (Königsberg, 5 dicembre 1868 – Monaco di Baviera, 26 aprile 1951)
.
3.6 L'atomo di Sommerfeld
Anche il modello atomico di Niels Bohr tuttavia contiene delle smagliature. Aumentando infatti la risoluzione si osservò che le righe della serie di Balmer erano in realtà degli insiemi di righe: la riga Hα dell'idrogeno, cioè la prima della serie di Balmer, appare come un doppietto di due righe, spaziate di 0,33 cm–1. Il modello di Bohr non è assolutamente in grado di spiegare questa spaziatura; fu il tedesco Arnold Sommerfeld (1868-1951) ad intuire che, per spiegare quella che egli chiamò la struttura fine delle righe spettrali, era indispensabile recuperare l'ellitticità delle orbite elettroniche. In base alle leggi di Kepler, infatti, un corpo soggetto a forze centrali si muove su orbite ellittiche, come abbiamo discusso in un altro mio ipertesto; l'energia dipende dal semiasse maggiore delle orbite, mentre l'eccentricità dipende dal momento angolare. Esistono dunque orbite caratterizzate dalla stessa energia, ma da forme differenti. Qui sotto si vede la forma reale della riga Hα; essa mostra che anche le possibili forme delle orbite sono quantizzate.

Questa eccentricità è caratterizzata da un secondo numero quantico, detto numero quantico secondario l, ed il momento angolare dell'orbita elettronica è dato da:
![]()
Il livello caratterizzato dal numero quantico principale è n volte degenere, cioè l è legato ad n dalla relazione:
![]()
Se n = 4, per esempio, l può valere 0, 1, 2 o 3: ci sono cioè quattro valori possibili per l. Dovete fare attenzione a non confondervi: K, L, M, N... sono i livelli energetici di Bohr, contrassegnati dai valori successivi di n, mentre i successivi valori di l corrispondono ai valori che il momento angolare degli elettroni può assumere, quando essi ruotano dentro quei ben definiti livelli energetici. All'interno di ogni livello energetico o shell, caratterizzato da un certo valore di l, possono esistere diverse orbite ellittiche, tutte con la stessa energia ma con momenti angolari diversi, cioè con eccentricità (e quindi con forme) diverse. Tali orbite (che, come vedremo, nel modello atomico quantistico prenderanno il nome di orbitali) sono indicate con lettere minuscole; le prime quattro sono indicate con s, p, d, f, e le altre con lettere in ordine alfabetico crescente, come mostra la tabella sottostante:
|
l |
|
simbolo |
|
0 |
0 |
s |
|
1 |
√2 |
p |
|
2 |
√6 |
d |
|
3 |
√12 |
f |
|
4 |
√20 |
g |
|
5 |
√30 |
h |
|
6 |
√42 |
i |
L'orbita s è circolare (il corrispondente orbitale avrà simmetria sferica), gli altri sono sempre più ellittici all'aumentare di l, come mostra la figura sottostante; la Meccanica Quantistica ci dirà che i corrispondenti orbitali avranno forme assai più complicate.
La shell K ha n = 1, quindi può contenere solo l'orbita con l = 0, che è l'orbita s.
La shell L ha n = 2, quindi può contenere due orbite con l = 0 ed l = 1, cioè s e p.
La shell M ha n = 3, quindi può contenere tre orbite con l = 0, l = 1 o l = 2, cioè s, p e d.
La shell N ha n = 4, quindi può contenere quattro orbite con l = 0, l = 1, l = 2 o l = 3, cioè s, p, d e f. E così via.
Attualmente non ci sono noti elementi chimici che hanno elettroni nelle orbite (cioè negli orbitali) g, h e i, ma è comunque possibile eccitare gli elettroni degli atomi noti fino a portarli in questi stati con momento angolare molto alto.

Il fatto che le orbite siano ellittiche rimuove la degenerazione delle righe spettrali. Infatti, in base alla Seconda Legge di Kepler, l'elettrone è più veloce allorché è più vicino al nucleo, mentre è costante la sua velocità areolare, cioè l'area "spazzata" dalla congiungente elettrone-nucleo nell'unità di tempo. Dunque la velocità dell'elettrone muta durante la sua orbita; ciò implica una variazione della massa dell'elettrone, poiché esso si muove a velocità confrontabili con quelle della luce, e quindi si ha una variazione relativistica della massa. La massa aumenta quando la distanza dal nucleo diminuisce, e viceversa; allora l'energia di legame (che è negativa) aumenta, e quindi l'energia totale diminuisce. Se ne deduce che le orbite non sono chiuse: la variazione relativistica della massa produce quella che in astronomia si chiama la precessione del perielio (o meglio del "perinucleo"):

Per questo, Sommerfeld introdusse nel 1916 una nuova costante pari al rapporto tra la velocità dell'elettrone sulla prima orbita di Bohr e la velocità della luce c. Dalla (3.3) si ricava:

E per n = 1 si ha:
![]()
Questa è quella che abbiamo già chiamato costante di struttura fine, arbitrariamente introdotta in quel che precede: ecco perchè la avevamo battezzata così! Si tratta di una costante adimensionale, il cui valore più preciso oggi noto è:
α = 1 / 137,0359991
Essendo adimensionale, la costante α ha un'importanza fondamentale nella fisica teorica: l'esistenza stessa di questa costante viene interpretata da alcuni fisici come un indizio dell'incompletezza del nostro Modello Standard. Le costanti non adimensionali sono difatti associate a convenzioni nelle unità di misura e dipendono dalla scelta delle stesse. Una costante adimensionale, al contrario, è indipendente dall'unità di misura e appare come un fattore arbitrario in una teoria. Nella storia della scienza, quasi tutte le costanti adimensionali a un certo punto sono state eliminate grazie a un ampliamento della teoria in cui apparivano. Per esempio, le costanti dielettriche relative dei materiali possono essere calcolate con i moderni modelli della struttura della materia. Tuttavia non esiste oggi una spiegazione della costante α a partire da altre teorie, ed è uno dei tanti parametri del modello standard che devono essere determinati sperimentalmente, tanto che il famoso fisico Richard P. Feynman ha dichiarato:
« Questa costante ha rappresentato un mistero fin dalla sua scoperta avvenuta più di cinquant'anni fa, e tutti i fisici teorici appendono questo numero sulla parete di fronte a loro e si interrogano sul suo significato. Vorremmo sapere immediatamente da dove viene, ma nessuno lo sa. É uno dei più grandi dannati misteri della fisica: un numero magico donato all'uomo, che non lo sa comprendere »
La costante di struttura fine venne acquistando negli anni una molteplicità di significati, alcuni addirittura dal sapore esoterico, narrate nel saggio di Arthur J. Miller "L'equazione dell'anima" (2009). Infatti agli inizi l'incertezza sperimentale fece illudere alcuni fisici che α fosse esattamente uguale a 1/136. Arthur Eddington (1882-1944), il famoso studioso di Relatività Generale, ne dedusse in qualche modo che il numero dei protoni dell'universo fosse precisamente 136 x 2256, noto come "numero di Eddington", cioè circa 1079. In seguito, Wolfgang Pauli (1900-1958) e Carl Gustav Jung (1875-1961) notarono che nella gematria, un'antica tecnica cabalistica che studia i valori numerici delle parole (nell'alfabeto ebraico ad ogni lettera corrisponde un certo valore numerico), 137 è il numero della parola Kabbalah (in ebraico «kblh» e quindi 100 + 2 + 30 + 5 = 137), e ne ricavarono altre conseguenze esoteriche e metafisiche che ben poco hanno a che fare con la Fisica. Per uno scherzo del destino, il 15 dicembre 1958 Pauli morì proprio nella stanza 137 dell'Ospedale di Zurigo, a soli 58 anni!
Per tornare alla Fisica, l'elettrone sul livello energetico fondamentale di un atomo di idrogeno si muove a circa 2200 km/s, e su quello di un atomo di elio a velocità doppia; e poiché l'aggiunta di ogni protone nel nucleo aumenta di uno il numeratore della frazione che determina la costante di struttura fine, se ne deduce che un atomo non può avere più di 137 protoni, altrimenti la velocità di un elettrone che gira nel suo stato fondamentale sarebbe superiore a quella della luce. Di conseguenza, benché finora la tavola periodica degli elementi sia già arrivata all'elemento 118, non potrà andare oltre l'eventuale elemento 137, già battezzato feynmanio dai fisici. La costante di struttura fine sta acquistando sempre più importanza anche in cosmologia, in quanto ha un ruolo importante nella teoria delle stringhe e del multiverso. Inoltre gran parte della sua rilevanza è legata al principio antropico; infatti questo parametro adimensionale ha un ruolo fondamentale nella vita dell'universo. Se il suo valore fosse diverso anche di poco dal valore noto, l'universo sarebbe molto diverso da come lo vediamo, e le leggi fisiche differirebbero parecchio da come le conosciamo: ad esempio, i rapporti tra le forze attrattive e repulsive tra le particelle elementari sarebbero diversi, con conseguenze sulla costituzione della materia e l'attività delle stelle. In un universo con α differente, noi stessi non potremmo esistere. La spiegazione più semplice però è questa: in universi dove il valore di α è incompatibile con la vita, non vi è nessun essere intelligente e di conseguenza nessuno che possa misurare quei valori di α!
3.7 L'esperienza di Stern e Gerlach
Due numeri quantici però non bastano ancora per spiegare la complessa struttura degli atomi. Un elettrone che ruota intorno al suo nucleo infatti può essere considerato una spira percorsa da corrente elettrica. Il periodo di rotazione dell'elettrone è pari a T = 2 π / ω, per cui tale corrente può essere ritenuta pari a:
![]()
Ogni spira ha un momento di dipolo magnetico, avente modulo ( i A ), dove A = π r2 è l'area della spira, la sua direzione è ortogonale al piano della spira ed il suo verso è dato dalla regola della mano destra (le prime quattro dita nel verso della corrente, il pollice nel verso del momento magnetico) per cariche positive, il contrario per cariche negative. Di conseguenza:
![]()
Ma si sa che:
![]()
e quindi:
Per l'elettrone nella prima orbita di Bohr (l'orbita, o meglio l'orbitale s della shell K) si sa che:
![]()
di conseguenza:
![]()
Questo momento magnetico è detto magnetone di Bohr μB, e vale:

I momenti magnetici degli elettroni nell'atomo vengono misurati in unità μB. Dalla precedente segue che μL, la componente del vettore μ lungo il vettore L, è così quantizzata:
![]()
È però possibile dimostrare che questa NON è l'unica quantizzazione possibile del vettore momento magnetico degli elettroni: per farlo si ricorre alla esperienza di Stern e Gerlach. Esso prende nome da Otto Stern (1888-1969) e Walther Gerlach (1889-1979), i quali nel 1921 studiarono la deflessione dei fasci atomici che attraversano campi magnetici non uniformi. Allo scopo essi produssero mediante un forno un fascio di atomi d'agento vaporizzato e lo fecero passare attraverso un campo magnetico, il cui modulo e la cui direzione cambiano da punto a punto mediante espansioni polari non piane, come si vede nello schema sottostante:

Se il campo magnetico è omogeneo, il momento magnetico μB e il momento angolare L subiscono una precessione attorno al campo B con una frequenza detta frequenza di Larmor. Se però il campo non è omogeneo, sul dipolo magnetico agisce anche una forza la cui intensità e la cui direzione dipendono dall'angolo tra il campo magnetico B e il momento magnetico μB. Un dipolo parallelo al campo avverte una forza diretta nel verso in cui il campo è crescente, mentre su un dipolo perpendicolare al campo non agisce alcuna forza.
Ci si aspetterebbe che gli atomi si distribuiscano uniformemente sullo schermo, perchè in teoria il momento magnetico degli elettroni potrebbe essere inclinato in tutte le maniere possibili. Invece, Stern e Gerlach osservarono un incredibile sdoppiamento degli atomi sullo schermo. Ciò può essere spiegato solo ammettendo che μ può essere orientato solamente in certi particolari modi rispetto a B. Chiamando z l'asse lungo cui è diretto B, avremo precisamente:
![]()
dove:
![]()
Dunque le orientazioni spaziali del vettore μ, e quindi delle orbite, sono quantizzate anch'esse; m si dice il numero quantico magnetico, e dipende dai valori di l.
Qui sotto potete vedere la riproduzione di una cartolina datata 8 febbraio 1922 e spedita da Walther Gerlach a Niels Bohr. Essa mostra una fotografia dello sdoppiamento del fascio, con la dicitura: « ...la prova sperimentale della quantizzazione direzionale. Mi congratulo con voi per la conferma della vostra teoria » (da "Physics Today" del dicembre 2003, tratta da questo sito).

Analizziamo i possibili valori di m. L'elettrone della shell K può avere solo l = 0, e quindi m = 0. Dunque abbiamo una sola orientazione possibile, e non c'è da stupirsene, dal momento che si tratta di un'orbita circolare!
Un elettrone con l = 1 (come minimo si trova nella shell L), cioè nell'orbita p, può avere m = 1, m = 0 ed m = – 1, corrispondenti (vedi figura sottostante) a tre orientazioni possibili di μ rispetto a B.
Un elettrone con l = 2 (come minimo si trova nella shell M), cioè nell'orbita d, può avere cinque valori di m: m = 2, m = 1, m = 0 ed m = – 1, m = – 2, corrispondenti (vedi figura) a cinque orientazioni diverse dell'orbita. E così via.

Questo significa che la sottoshell s contiene al massimo una orbita (oggi diremmo orbitale) circolare, la sottoshell p contiene al massimo un'orbita circolare e tre ellittiche, la sottoshell d contiene almeno un'orbita circolare, tre ellittiche con eccentricità minore e cinque ellittiche con eccentricità maggiore, e così via. Ma non è finita.
3.8 Lo spin dell'elettrone
Infatti gli stati con n = 0, l = 0 ed m = 0 dovrebbero avere momento angolare e magnetico nullo, ed invece l'esperienza mostra che anche i fasci di atomi di idrogeno nello stato fondamentale si sdoppiano, se immersi in campo magnetico. Ciò vuol dire che anche gli elettroni su quell'orbita devono possedere un momento magnetico, seppur minimo.
George Eugene Uhlenbeck (1900-1988) e Samuel Abraham Goudsmith (1902-1978), fisici olandesi naturalizzati statunitensi, ebbero l'idea che l'elettrone possieda un momento magnetico intrinseco, che non potevano spiegare altrimenti se non attraverso una rotazione dell'elettrone sul proprio asse. Finora infatti abbiamo pensato all'elettrone come ad un oggetto puntiforme, ma esso dovrebbe pure avere una propria estensione. Si definisce raggio classico dell'elettrone quello calcolato come se l'energia potenziale elettrostatica della sua carica superficiale coincidesse con la sua energia relativistica a riposo. Sarà allora:

da cui si ricava:
![]()
Occorre chiarire bene che questo risultato è frutto di una mera ipotesi; tuttavia, le esperienze di diffrazione di raggi X assegnano all'elettrone più o meno un raggio dello stesso ordine di grandezza re. Invece, le misure di diffrazione di elettroni contro altri elettroni non hanno mostrato deviazioni significative dalla legge di Coulomb, neppure per parametri d'urto molto piccoli; segno, questo, del fatto che finora l'elettrone non ha rivelato alcuna struttura interna, nonostante le ipotesi di alcuni fisici (il cosiddetto modello a preoni).
Nel 1925 Wolfgang Pauli (1900-1958) ipotizzò la quantizzazione del momento angolare intrinseco dell'elettrone, attraverso un numero quantico ms:
![]()
Questo momento è detto anche momento di spin, dall'inglese "trottola", perchè l'elettrone si comporterebbe come una trottola, che piroetta intorno al suo asse. L'introduzione di un quarto numero quantico suscitò alcune perplessità, ma Uhlenbeck fece osservare che, se l'elettrone ha tre gradi di libertà, per descrivere il suo moto bastano tre numeri quantici; se ne introduco un quarto, devo postulare un moto di rotazione intrinseco dell'elettrone, e cioè appunto la rotazione su se stesso.
Naturalmente, analogamente a quanto fatto per il momento magnetico orbitale, anche la componente lungo z del momento magnetico di spin deve essere quantizzata:
![]()
dove:
![]()
per analogia con quanto visto prima. Ma il fascio elettronico si sdoppia in due; siccome la molteplicità di questo momento magnetico, cioè il numero delle proiezioni indipendenti sull'asse z, è ( 2 ms + 1 ), ne segue:
![]()
da cui ms = 1 / 2. Di conseguenza:
![]()
Questo si chiama numero quantico di spin, e può assumere solo due valori (di ms, che è costante, ci dimenticheremo). Se s = + 1 / 2, si dice che l'elettrone ha uno SPIN UP; se s = – 1/ 2 invece ha uno SPIN DOWN. Come mostra la figura, ciò corrisponde a due possibili modi di ruotare dell'elettrone!

Abbiamo così in tutto quattro numeri quantici:
i)
n quantizza l'energia, cioè i semiassi
maggiori delle orbite elettroniche
ii) l quantizza il momento angolare orbitale,
cioè l'eccentricità delle orbite
iii) m quantizza la componente lungo z
del momento angolare orbitale, cioè l'orientazione
spaziale delle orbite
iv) s quantizza la componente lungo z del
momento angolare di spin, cioè il verso di
rotazione dell'elettrone su se stesso
Se però andiamo a cercare il momento magnetico intrinseco dell'elettrone, ci accorgiamo che esso vale:
![]()
che differisce dalla (3.8) solo per il fattore gs, detto fattore g dell'elettrone, che vale:
gs = 2,0023
Secondo la fisica classica, come nella (3.8), esso dovrebbe valere uno. Ma, nella fisica tradizionale, questo valore NON ha spiegazione.
Il fatto è che nel 1928 il fisico britannico Paul Adrien Maurice Dirac (1902-1984) dimostrò che lo spin dell'elettrone non ha niente a che vedere con un fenomeno meccanico come la rotazione dell'elettrone su se stesso, bensì è conseguenza piuttosto di un effetto relativistico, per via dell'altissima velocità dell'elettrone. Il fattore g infatti salta fuori in maniera assolutamente naturale nell'ambito della meccanica quantistica relativistica, che tiene conto anche dell'elevata velocità delle particelle quantistiche, e di cui Dirac fu appunto il padre, come vedremo nel capitolo 9.

Che il concetto di "atomo" sia diventato celeberrimo anche nella cultura popolare lo dimostra l'invenzione, da parte della DC Comics, di un supereroe chiamato Atomo (in inglese "Atom" o "Captain Atom"), che ha esordito su All-American Comics n. 19 dell'ottobre 1940. Fu interpretato in origine da Al Pratt, personaggio immaginario ispirato alla vita di Joe Greenstein (1893-1977), conosciuto come "Il Potente Atomo", personaggio reale di piccola statura, culturista e pugile autodidatta per contrastare la salute cagionevole dell'infanzia. Inizialmente Al Pratt era un ragazzo molto gracile, ma poi venne preparato a combattere dall'ex pugile Joe Morgan ed acquisì superpoteri come risultato dei latenti effetti della sua battaglia con il criminale Cyclotron. Si noti che i fumetti di questo piccolo supereroe sono costellati da raffigurazioni del modello quantomeccanico dell'atomo!

Mi sembra giusto chiudere questa pagina con un sorriso, ricordando un'altra "incarnazione fumettistica" dell'atomo di Bohr e Sommerfeld: Atomino Bip Bip, personaggio Disney che rappresenterebbe un atomo ingrandito « due birilliardi di volte » grazie ad un macchinario chiamato Bambatrone, ideato dal professor Enigm! Il 10 marzo 2019 questo personaggio ha compiuto esattamente sessant'anni, essendo stato creato dal grande fumettista Romano Scarpa (1927-2005) nell'avventura "Topolino e la Dimensione Delta" (su "Topolino" numero 206 del 10 marzo 1959).
.
Fin qui arriva il modello quantomeccanico. Per andare oltre, bisognerà parlare del dualismo onda-particella, e lo faremo nel prossimo capitolo. Per tornare all'indice, il link è questo.
