

|
"I progressi nel campo della fisica si ottengono negando l’ovvio e accettando l’impossibile." Robert A. Heinlein (1907-1988) |
.
2.1 La catastrofe ultravioletta
Tutti i fenomeni legati all'ottica ed alla teoria del campo elettromagnetico sono inquadrabili in quella che va sotto il nome di Fisica Classica. Verso la fine del XIX ed al principio del XX secolo, tuttavia, vennero effettuati alcuni importanti esperimenti, i quali misero in luce l'impossibilità da parte della Fisica Classica di spiegare tutti i fenomeni della natura, contrariamente a quanto speravano i filosofi positivisti dell'ottocento. Per questo divenne indispensabile elaborare una teoria più generale e completamente innovativa, e cioè la Teoria dei Quanti. Questi fenomeni sono essenzialmente quattro:
i) la
radiazione di corpo nero;
ii) l'effetto fotoelettrico;
iii) gli spettri di emissione degli atomi;
iv) l'effetto Compton.
In questo capitolo discuteremo del primo, del secondo e del quarto fenomeno, mentre al terzo dedicheremo il prossimo capitolo.
Si dice corpo nero un corpo che assorbe completamente qualunque radiazione ricevuta. Ogni corpo, una volta riscaldato, emette radiazioni elettromagnetiche, il cui spettro (cioè l'insieme delle loro frequenze) dipende fondamentalmente dalla natura del corpo preso in esame. È infatti esperienza quotidiana il fatto che, arroventando un corpo, esso si riscalda e comincia ad emettere una radiazione che varia dal rosso scuro al rosso brillante, per giungere al giallo e al bianco man mano che la temperatura sale: non a caso si parla di "calor bianco"! Del resto, il termine italiano "arroventare" deriva dal latino "ruber", "rosso", e anche il termine "incandescente" deriva dal latino "candesco", cioè "divento bianco" (la stessa radice etimologica di "candido"). Dal colore del metallo dentro un forno è allora possibile risalire alla temperatura da esso raggiunta: tale tecnica è detta pirometria.
In realtà, l'emissione di un corpo caldo non può essere e non è esclusivamente luminosa. Al di sotto di poche centinaia di Kelvin, l'emissione è esclusivamente infrarossa; ciò spiega perchè si può "vedere anche al buio", usando un visore sensibile ai raggi infrarossi. Questa radiazione infrarossa è quella che fa sì che un corpo termicamente isolato (per quel che riguarda la conduzione e la convezione) raggiunga rapidamente la condizione di equilibrio termico con l'ambiente, come ho spiegato nell'ipertesto "La pentola di Papin", dedicato alla Termodinamica. Ecco perché, per effettuare esperimenti a temperature assai basse, superiori soli di pochi Kelvin allo zero assoluto, è necessario schermare termicamente le strutture dalle radiazioni infrarosse nel laboratorio.
Le leggi che governano la distribuzione spaziale della radiazione termica sono state sostanzialmente ottenute proprio dall'analisi della radiazione emessa da un corpo nero. Un modo molto semplice per schematizzare un corpo nero è quello di usare una cavità nella quale la radiazione è in equilibrio termico con le pareti, le quali cioè mediamente emettono tanta radiazione quanta ne assorbono. Un buon modello di corpo nero è una bottiglia affumicata dal collo molto stretto: la radiazione che la colpisce sulla superficie esterna colorata di nero viene immediatamente assorbita, mentre quella che attraversa la sua imboccatura è rapidamente assorbita dalla superficie interna perchè, riflettendosi innumerevoli volte, ha scarsa probabilità di trovare la strada per fuoriuscire, e viene completamente assorbita prima di riuscirci.
Tutti noi nella nostra vita abbiamo avuto l'occasione di osservare questo fenomeno con i nostri occhi. Infatti, una chiesa si comporta proprio come un corpo nero! Se non ci credete, osservate la foto sottostante: in una giornata di sole il portale spalancato di una chiesetta di Castano Primo, non lontano da dove abita l'autore di questo ipertesto, ci mostra il suo interno completamente nero. La spiegazione è molto semplice: tutti i raggi di luce che penetrano nella chiesa attraverso il portale sono assorbiti dalle pareti interne, prima che riescano a ritrovare la strada per fuoriuscire all'esterno! E lo stesso può dirsi per le finestre di una casa, o per l'interno di un container, osservati in una giornata soleggiata. Quando si dice: la Fisica è dappertutto, intorno a noi!

Per studiare l'emissione di corpo nero occorrerà fare uso di alcuni strumenti dell'Analisi Matematica. Chiamiamo dunque u(f,T) df la densità di energia per unità di volume associata, a temperatura T, ad una radiazione di corpo nero con frequenza compresa tra f e f + df. Se rappresentiamo l'intensità della radiazione emessa, ci accorgiamo che lo spettro è continuo, e presenta un massimo per una certa frequenza fmax, che aumenta all'aumentare della temperatura. In particolare, la lunghezza d'onda λmax corrispondente a questa frequenza massima è data dalla legge dello spostamento, detta anche legge di Wien, elaborata nel 1893 dal fisico tedesco Wilhelm Wien (1864-1928):
dove b è la costante di Wien:
b = 2,898 x 10–3 m K
Per esempio, nel caso del nostro Sole si osserva che il massimo di emissione si osserva sulla frequenza di 625 milioni di MHz, che corrisponde ad una lunghezza d'onda di:
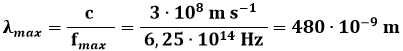
cioè di 480 nanometri. La legge di Wien ci permette allora di ricavare la temperatura superficiale del nostro Sole:
![]()
Sia detta P(f,T) df l'energia trasportata da un fascio di onde elettromagnetiche attraverso un elemento di area unitaria, perpendicolarmente alla direzione di propagazione del fascio stesso, per unità di superficie e di angolo solido. La relazione tra u e P dentro la cavità è:
![]()
Se misuro P in uscita dal foro, posso risalire facilmente ad u. Integrando l'espressione di P(f,T) su tutte le frequenze e su tutti gli angoli solidi, si ottiene infatti l'energia totale della radiazione E, la cui espressione è molto semplice:
E = σ T4 (2.2)
dove σ è detta costante di Stefan-Boltzmann:
σ = 5,67 x 10–8 W m–2 K–4
La legge ora ricavata è detta legge di Stefan-Boltzmann, e fu trovata per via empirica nel 1879 dallo sloveno Josef Stefan (1835-1893) e dall'austriaco Ludwig Boltzmann (1844-1906).
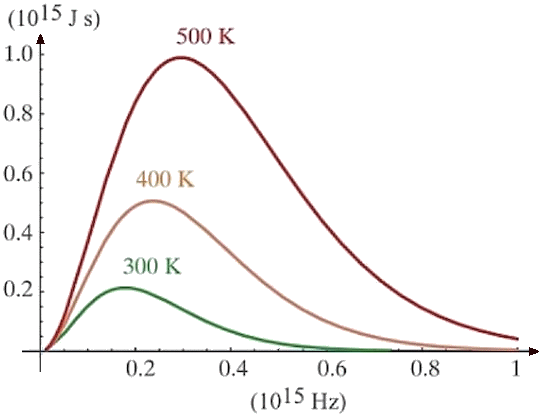
Come si può vedere dal diagramma qui sopra, l'intensità della radiazione emessa dal corpo nero, cioè P(f,T), misurata sperimentalmente, diminuisce sia per le alte che per le basse frequenze. Se però si tenta di interpretare questo comportamento alla luce dell'elettromagnetismo classico, sintetizzato nelle quattro Equazioni di Maxwell, si trovano risultati in netto contrasto con l'esperienza. Sfruttando l'elettrodinamica classica, ed ipotizzando che tutte le molecole della cavità siano oscillatori armonici, simili a piccolissime cariche elettriche collegate agli atomi mediante molle, John William Strutt, terzo Baron di Rayleigh (1842-1919) e Sir James Hopwood Jeans (1877-1946) elaborarono la seguente formula, detta Legge di Rayleigh e Jeans:
![]()
che, come mostra il digramma seguente, è in accordo con l'esperienza solo a basse frequenze:
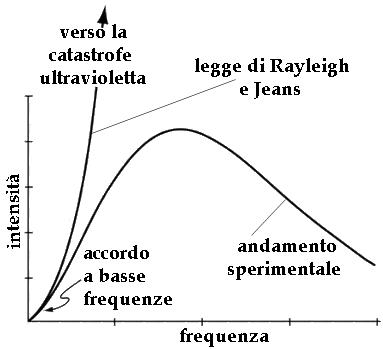
Infatti, se integriamo la Legge di Rayleigh e Jeans su tutte le frequenze, otteniamo paradossalmente un risultato infinito. Ciò significa che l'intensità dovrebbe crescere indefinitamente all'aumentare della frequenza! Se ciò fosse vero, accadrebbe quella che è nota con il termine di catastrofe ultravioletta: termine drammatico che esprime il paradosso in base al quale anche un comune forno domestico, se scaldato ad oltranza, diventerebbe una pericolosissima sorgente di raggi ultravioletti, che vengono subito dopo il violetto nello spettro elettromagnetico; e per temperature via via crescenti, anche di terribili raggi X e raggi gamma!
Nessuno però è mai morto per essersi dimenticato acceso il forno in cucina. Evidentemente, nella Fisica Classica qualcosa non andava: la pretesa ottocentesca di aver in mano la chiave per interpretare ogni fenomeno dell'universo naufragò miseramente di fronte alla radiazione emessa da una cavità surriscaldata. Questa impotenza concettuale fu definita da Lord Kelvin « la nuvola nera che oscurava il cielo della Fisica »! Eppure, storicamente sono state proprio le "gambe zoppicanti" delle teorie fisiche credute perfette infallibili, a permettere di compiere le più straordinarie rivoluzioni della storia della conoscenza umana!
.
2.2 Arriva Max Planck
La soluzione della mancata catastrofe ultravioletta fu ottenuta per la prima volta dal tedesco Max Planck (858-1947), professore dell'Università di Berlino con il suo celebre lavoro « Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum » ("Sulla teoria della distribuzione dell'energia nello spettro normale"), nel quale riuscì ad interpretare correttamente lo spettro del corpo nero, a patto però di capovolgere completamente i fondamenti su cui si basava tutta la Fisica Classica. Fin dai tempi di Aristotele, infatti, la Natura era considerata fondamentalmente continua; è di Gottfried Leibniz (1646-1716) il famoso motto latino « Natura non facit saltus », che condizionò generazioni di pensatori. L'energia, così come compare nelle Equazioni di Maxwell, nei principi della Dinamica e nella Termodinamica, può essere scambiata in quantità qualsiasi, senza alcuna limitazione, e i suoi valori possono variare con continuità dentro un certo intervallo continuo. Secondo Planck, invece, gli oscillatori armonici atomici possono scambiare con la radiazione pacchetti energetici che sono unicamente multipli interi di un'unità fondamentale, detto quanto di energia, il cui valore è pari a:
E = h f
 dove
f è la frequenza ed h è una costante universale, detta
costante di Planck. Come misurarne il valore?
Suggeriamo un metodo possibile. Consideriamo un LED (Light Emission Diode),
un diodo in grado di emettere luce ogni volta che un elettrone si ricombina con
una lacuna. Il LED da noi preso in considerazione emette luce con una lunghezza
d'onda di 465 nanometri (luce azzurra), e
quindi con una frequenza di circa 6,45 x 1014 Hz. Alimentiamo
il LED con un circuito contenente un reostato, cioè
una resistenza variabile: mentre uno sperimentatore muove con grande lentezza il
cursore del reostato, noi osserviamo il LED per stimare quando esso inizia ad
accendersi; per rendere più facile apprezzare questo momento, il locale in cui
avviene l'esperimento è stato opportunamente oscurato, in modo che esso sia
immerso nella penombra. Nel momento esatto in cui il LED azzurro comincia ad
illuminarsi, si registra la tensione ai suoi estremi mediante un comune
voltmetro. Scopriamo che tale tensione corrisponde approssimativamente a 2,67
V. Allora l'energia del singolo elettrone che attraversa il fotodiodo è pari
a:
dove
f è la frequenza ed h è una costante universale, detta
costante di Planck. Come misurarne il valore?
Suggeriamo un metodo possibile. Consideriamo un LED (Light Emission Diode),
un diodo in grado di emettere luce ogni volta che un elettrone si ricombina con
una lacuna. Il LED da noi preso in considerazione emette luce con una lunghezza
d'onda di 465 nanometri (luce azzurra), e
quindi con una frequenza di circa 6,45 x 1014 Hz. Alimentiamo
il LED con un circuito contenente un reostato, cioè
una resistenza variabile: mentre uno sperimentatore muove con grande lentezza il
cursore del reostato, noi osserviamo il LED per stimare quando esso inizia ad
accendersi; per rendere più facile apprezzare questo momento, il locale in cui
avviene l'esperimento è stato opportunamente oscurato, in modo che esso sia
immerso nella penombra. Nel momento esatto in cui il LED azzurro comincia ad
illuminarsi, si registra la tensione ai suoi estremi mediante un comune
voltmetro. Scopriamo che tale tensione corrisponde approssimativamente a 2,67
V. Allora l'energia del singolo elettrone che attraversa il fotodiodo è pari
a:
E = e ΔV = 1,6 x 10–19 C x 2,67 V = 4,272 x 10–19 J
Allora dalla formula di Planck risulta facile ricavare il valore di h:
h = E / f = 4,272 x 10–19 J / 6,45 x 1014 Hz = 6,62 x 10–34 J s
Il valore oggi comunemente accettato di h è pari a:
h = 6,62606957 x 10–34 J = 4,1356675 x 10–15 eV s
Questa costante, come un fantasma, appare tutte le volte che si studia un fenomeno nel mondo dell'infinitamente piccolo, dimostrando così che tutto questo mondo è dominato dagli scambi energetici discreti. Risulta allora abbastanza naturale comprendere perchè nel nostro mondo macroscopico tale discontinuità non è avvertibile: i "salti" energetici sono troppo piccoli perchè noi possiamo rilevarli, ed a noi le transizioni energetiche appaiono continue!

|
Topolino, Pippo e Max Planck disegnati da Alessandro Perina nell'avventura a fumetti "Topolino e l'esperimento del Dottor Pi" pubblicata su "Topolino" n° 3175 del 28 Settembre 2016! Planck è visibile al centro; alla sua destra è disegnato Hendrik Kramers (1894-1952), uno dei cui risultati è la formula di Kramers-Heisenberg sull’urto tra un fotone e un elettrone atomico, mentre alla sua sinistra c'è Édouard Herzen (1877-1936), uno dei più importanti fisici belgi. |
Planck calcolò la sua distribuzione come segue; per ripetere il suo ragionamento, dovremo utilizzare gli strumenti dell'Analisi Matematica. Se l'energia irraggiata assume valor discreti, il valore medio può essere calcolata così:
dove la probabilità che l'energia assuma il valore E è data da:
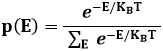
in base alla ben nota distribuzione di Maxwell-Boltzmann, della quale abbiamo parlato in questo paragrafo di un altro ipertesto. Chiamiamo ora E = n h f, dove n è un numero intero, e poniamo:
![]()
La precedente allora diventa:
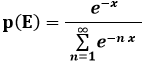
Ora, quella a denominatore è una progressione geometrica di periodo e–x, e la sua somma è pari a:
![]()
Ne segue che la probabilità suddetta è pari a:
![]()
Sostituiamo ora nell'espressione (2.3) del valor medio dell'energia < E >:
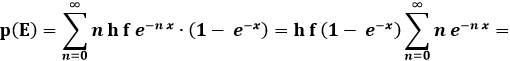
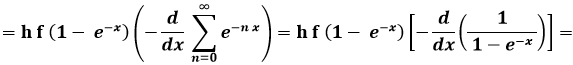
![]()
Risostituiamo il valore di x e troviamo:
Ora, la radiazione nella cavità del corpo nero si può considerare come un'onda stazionaria di vettori campo elettrico E e campo magnetico B. Decomponendo tali vettori nei loro modi normali, è come se tra le frequenze f e f + df operasse un numero dn di oscillatori armonici classici, pari a:
![]()
Per il teorema di equipartizione dell'energia (vedi quest'altro mio ipertesto), ogni oscillatore della cavità all'equilibrio termodinamico ha un'energia pari a < E >. Si ha dunque:
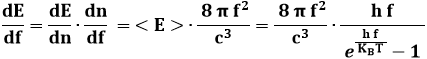
E quindi:
Se rappresentiamo questo andamento, ci accorgiamo che è in ottimo accordo con i dati sperimentali, a differenza della Legge di Rayleigh e Jeans! Lo dimostra questo grafico, nel quale la curva di emissione del nostro Sole è comparata con la distribuzione di Planck ora ricavata per la temperatura di 6037 K calcolata qui sopra:
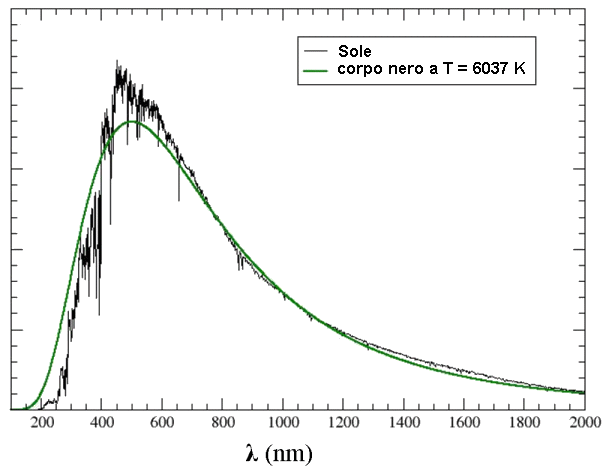
A basse frequenze, cioè se h f << KB T, usando gli sviluppi di MacLaurin si ha:
![]()
e quindi:
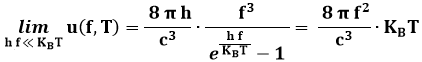
che è la previsione fatta da Rayleigh e Jeans. Se invece h f >> KB T, prevale l'esponenziale e si ha:
![]()
funzione che rispecchia bene l'andamento sperimentale per alti valori di f.
Se poi integriamo u(f,T) su tutte le frequenze, riutilizzando la sostituzione già sfruttata, si ha:

Per risolvere tale integrale improprio, seguiamo il seguente procedimento:
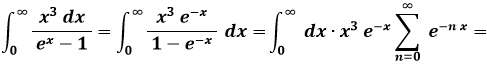
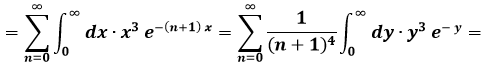
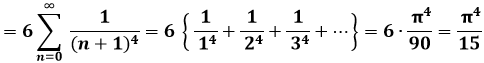
e quindi è immediato ottenere:
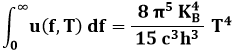
Se ne deduce che il potere emissivo totale del corpo nero è proporzionale alla quarta potenza della temperatura assoluta, in accordo con la legge di Stefan-Boltzmann. Siccome si può dimostrare che:
![]()
ne segue che la costante empirica di Stefan-Boltzmann è così interpretabile in funzione delle principali costanti fisiche:
![]()
Sostituendo i valori numerici, si trova proprio σ = 5,67 x 10–8 W m–2 K–4 (provare per credere). Il suo vero significato è dunque comprensibile solo alla luce della teoria quantistica di Max Planck.
In verità, lo stesso Planck fu spaventato dal fatto che la sua teoria aveva scosso i fondamenti della Fisica Classica. Egli stesso ebbe a dire: « Si prova d'istinto qualche ripugnanza a rovinare le fondamenta delle teorie sui fenomeni elettrici e magnetici, che pure hanno trovato tante conferme sperimentali! » Rivoluzionario suo malgrado, egli dovette accettare che la sua scoperta mettesse a soqquadro l'edificio della Fisica. Naturalmente, se Planck era scettico nei confronti delle sue nuove ipotesi, è facile immaginare quanto lo fossero i suoi colleghi. Le sue teorie sui quanti furono perciò accantonate, fino a che non divenne chiaro che essi potevano rappresentare la chiave per penetrare per la prima volta i segreti del mondo atomico.
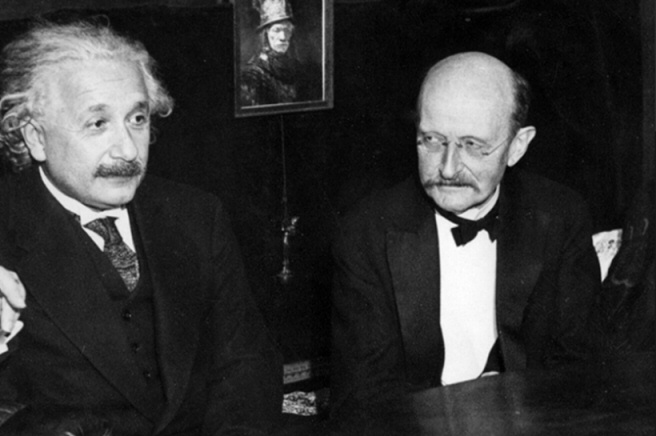
Max Planck (Kiel, 23 aprile 1858 – Göttingen, 4 ottobre 1947) con Albert Einstein
.
2.3 L'effetto fotoelettrico
Solo cinque anni dopo la prima ipotesi di Planck riguardo l'atomicità dell'energia trasportata dalla radiazione, il quanto di energia passò per la prima volta dal rango di "stranezza" a quello di realtà scientifica grazie ad un giovane dottore in Fisica del Politecnico di Zurigo. Quel giovane laureato era Albert Einstein, oggi considerato dall'opinione popolare come la personificazione stessa della Fisica, Nel 1905 egli pubblicò tre celeberrimi articoli articoli, il primo dei quali ha titolo « Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt », cioè « Su un punto di vista euristico circa la genesi e la trasformazione della luce » e riguarda l'effetto fotoelettrico (gli altri due articoli riguardano il moto browniano e la teoria della relatività ristretta).
Nel 1887 Heinrich Hertz (1857-1894), lo scopritore delle onde elettromagnetiche, osservò quasi per caso che, illuminando una placca di zinco con radiazione ultravioletta, il metallo si caricava elettricamente. Dopo la scoperta degli elettroni da parte di J.J. Thomson, si comprese che il metallo, colpito dai fotoni, generava un'emissione elettronica: l'effetto fotoelettrico, per l'appunto, così battezzato dall'italiano Augusto Righi (1850-1920). Nel 1900, lo stesso anno dell'ipotesi di Planck, l'effetto fotoelettrico fu studiato nei particolari da Philipp von Lenard (1862-1947), tristemente famoso per essere stato uno dei "fisici di regime" del nazismo e per aver duramente attaccato la Relatività di Einstein, definita una "fisica giudea". Egli utilizzò il seguente dispositivo:
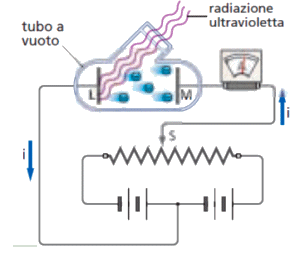
La luce viene prodotta da un arco voltaico, attraversa un collimatore ed è convogliata su di un prisma monocromatore, che seleziona una ben precisa lunghezza d'onda per rifrazione. Regolando l'inclinazione del prisma è possibile selezionare un pennello di radiazioni nell'ambito dei raggi ultravioletti. Attraverso una finestra di quarzo, materiale otticamente trasparente alla radiazione ultravioletta, il fascio di luce entra in un tubo a vuoto e colpisce una placca L, detta fotocatodo, costituita da un metallo alcalino come il cesio, che è caratterizzato da un potenziale di estrazione molto basso. La placca L emette allora elettroni che vengono raccolti da un collettore M, una placca opposta ad L, e danno vita ad una corrente facilmente misurabile dall'amperometro A. Questo dispositivo prende il nome di cella fotoelettrica.
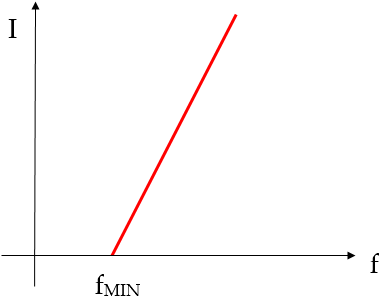
Tabuliamo ora i risultati dell'esperimento. Al di sotto di una certa frequenza di soglia fMIN, si osserva che non si ha alcuna emissione di fotoelettroni. Tale valore è caratteristico della natura del metallo, ed è chiamato soglia fotoelettrica. L'energia cinetica degli elettroni si può ricavare utilizzando il potenziale frenante di una pila, come nel circuito soprastante; regolando tale potenziale per mezzo di un reostato S, è possibile annullare la corrente fotoelettronica perchè gli elettroni non hanno più energia sufficiente per superare la barriera di potenziale. Se v è la velocità di emissione dei fotoelettroni, si ha:
![]()
Il potenziale frenante risulta direttamente proporzionale alla frequenza f; inoltre, al crescere di V l'intensità della corrente fotoelettronica cresce, ma poi tende a diventare costante, un valore tanto maggiore quanto maggiore è l'intensità luminosa incidente; e tale crescita è lineare.
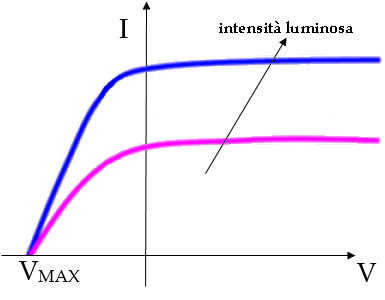

Sorprendentemente, questi risultati sono interpretabili solo utilizzando la teoria corpuscolare della luce! In altre parole, Einstein riportò in auge il vecchio modello proposto intorno all'anno 1000 da fisico iracheno Alhazen (vero nome Abū ʿAlī al-Ḥasan ibn al-Ḥasan ibn al-Haytham, 965-1039) e poi nel 1704 dal celebre Isaac Newton (1642-1727), i quali consideravano la luce composta da minuscoli corpuscoli, chiamati da Einstein fotoni, e che era stato superato ai primi dell'Ottocento, quando l'inglese Thomas Young (1773-1829) dimostrò la veridicità del modello ondulatorio della luce, proposto nel 1690 dall'olandese Christiaan Huygens (1629-1695), evidenziando i fenomeni di diffrazione ed interferenza dell'emissione luminosa. Ma perchè risuscitare il modello corpuscolare? Perché, da un punto di vista classico, il campo elettrico (proporzionale alla radice quadrata dell'intensità della radiazione) dovrebbe essere responsabile sia dell'accelerazione che dell'emissione degli elettroni dall'elettrodo; l'energia E dei fotoelettroni dovrebbe quindi aumentare al crescere dell'intensità luminosa e della potenza incidente, mentre l'esperienza dimostra che essa dipende solo ed esclusivamente dalla frequenza; il numero dei fotoelettroni emessi, viceversa, è proporzionale all'intensità luminosa, come si vede qui sotto. Ma soprattutto, l'effetto fotoelettrico è un "fenomeno a soglia", perché i fotoelettroni vengono emessi solo se la frequenza della luce supera un certo limite fMIN, un fatto assolutamente inspiegabile alla luce della sola teoria ondulatoria della luce, data per certa e comprovata ai primi del Novecento.
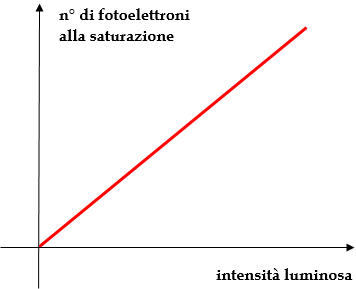
Supponiamo però che sia vera l'ipotesi di Planck, e che la luce sia composta da corpuscoli ciascuno dei quali ha energia h f. Quando uno di questi corpuscoli incide sul metallo (cesio nell'esperienza di Lenard), una parte della sua energia è spesa per estrarre l'elettrone dall'elettrodo metallico. Tale energia è il cosiddetto lavoro di estrazione WE, ed è pari a e VE, cioè al prodotto della carica dell'elettrone per il potenziale di estrazione, che è caratteristico di ogni materiale. Ecco il lavoro di estrazione di alcuni metalli e la frequenza minima alla quale corrisponde l'emissione di fotoelettroni:
|
elemento |
WE |
fMIN [1014 Hz] |
|
litio |
2,46 |
5,95 |
|
sodio |
2,28 |
5,51 |
|
potassio |
2,25 |
5,44 |
|
silicio |
4,85 |
11,72 |
|
rame |
4,48 |
10,83 |
|
argento |
4,26 |
10,30 |
|
platino |
5,36 |
12,95 |
|
mercurio |
4,48 |
10,83 |
L'energia rimanente contribuisce all'energia cinetica E dell'elettrone. Il bilancio energetico è il seguente:
![]()
dove il primo termine esprime l'energia cinetica del fotoelettrone, il secondo l'energia del fotone incidente, e il terzo l'energia di estrazione. Lo si può riscrivere più semplicemente:
![]()
Se rappresento in un diagramma cartesiano l'energia del fotoelettrone in funzione della frequenza, trovo un diagramma rettilineo come quello disegnato qui sopra, che interseca il semiasse verticale negativo delle energie in un punto pari proprio a – WE. La pendenza costante del grafico inoltre è pari alla costante h di Planck. In tal modo, usando l'ipotesi di Planck, Einstein interpretò con un ragionamento elegante e semplicissimo i risultati sperimentali, fornendo una conferma decisiva alla nascente Fisica dei Quanti.
Le applicazioni dell'effetto fotoelettrico sono molteplici: come esposimetri nelle macchine fotografiche, come contatori per misurare quante persone o auto attraversano una certa barriera, come dispositivi per azionare un cancello automatico o per far scattare il cronometro durante le competizioni sportive ("cellule fotoelettriche") e, in generale, per mettere in evidenza una variazione anche piccola e veloce di un effetto luminoso.
Si può aggiungere che fenomeni analoghi all'effetto fotoelettrico ora descritto, e noto anche come "effetto fotoelettrico esterno", si ritrovano nella Fisica dello Stato Solido, dove si ha un "effetto fotoelettrico interno". Esso consiste nella liberazione di portatori di carica da parte della radiazione; si osserva allora un aumento della conducibilità elettrica da parte dei semiconduttori. In Fisica Nucleare (vedi il mio ipertesto sulle Frontiere della Fisica) si studia anche il cosiddetto "effetto fotoelettrico nucleare", in cui il nucleo atomico, dopo aver assorbito un fotone gamma, si eccita ed emette un nucleone, cioè un protone o un neutrone.
.
2.4 L'effetto Compton
Da quel che precede si può concludere che la teoria ondulatoria della luce, così come fu formulata da Christiaan Huygens, è da ritenersi superata, perchè non spiega fenomeni come l'emissione di corpo nero e l'effetto fotoelettrico. D'altro canto, una visione puramente corpuscolare della radiazione è in netto contrasto con fenomeni quali la diffrazione e l'interferenza della luce. L'unica soluzione è quella che va sotto il nome di teoria corpuscolo-ondulatoria della propagazione luminosa: l'energia da essa trasportata è racchiusa in "pacchetti" discreti, che però si muovono lungo traiettorie ondulatorie. Questo ulteriore modello verrà poi superato dalla Meccanica Quantistica, che – come vedremo – considererà piuttosto l'onda come una distribuzione di probabilità di probabilità di trovare il corpuscolo nello spazio. Vediamo dunque un terzo fenomeno che, sebbene scoperto solo molti anni più tardi dei primi due, e quindi dopo i lavori di Niels Bohr sulla spettroscopia e sul modello atomico quantistico, ci costringe ad abbandonare il concetto di continuità caro alla Fisica Classica, per abbracciare l'ipotesi dei quanti di Max Planck. Si tratta dell'effetto Compton.

Arthur Compton (Wooster, 10 settembre 1892 – Berkeley, 15 marzo 1962)
Nel 1923 lo statunitense Arthur Compton (1892-1962) stava studiando la diffusione di raggi X da parte della materia. I raggi X sono radiazioni con lunghezza d'onda estremamente piccola, dell'ordine dell'Ǻngstrom, e quindi 100 volte più piccola della lunghezza d'onda della luce visibile. La frequenza, di conseguenza, è 100 volte più grande, e quindi tale radiazione porta con sé un'energia 100 volte più grande di quella della luce visibile. Siccome le distanze reticolari all'interno dei cristalli sono anch'esse dell'ordine dell'Ǻngstrom, i raggi X possono diffrangere attraverso i reticoli cristallini, e quindi possono essere usati per studiare la natura della materia.
Compton osservò che, se un fascio di raggi X incide su di una sottile lastra metallica, lo spettro diffuso è formato da radiazione con frequenza minore di quella incidente, mentre Lord Rayleigh aveva classicamente previsto che la radiazione diffusa avesse la stessa lunghezza d'onda di quella incidente. Compton allora ebbe l'idea che questo fenomeno fosse dovuto all'urto anelastico tra gli elettroni del metallo ed i quanti di luce. A prima vista la cosa appare stupefacente, poiché i fotoni sono privi di massa. È però vero che ad essi si può attribuire un impulso di natura relativistica. Se m è la massa relativistica del fotone, avremo:
![]()
e quindi:
![]()
da cui si ricava:
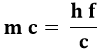
Questo è l'impulso del fotone, cioè la quantità di moto associata ad un fotone di frequenza f e velocità c. Ma allora, se l'elettrone possiede un impulso, può urtare contro gli atomi del metallo. Durante l'urto, esso perderà parte della propria energia, che si trasformerà in energia cinetica dell'elettrone, e rimbalzerà con la propria energia diminuita e la propria lunghezza d'onda aumentata:

Sia dunque f la frequenza del fotone incidente, e f ' < f quella del fotone diffuso. Se θ è l'angolo compreso tra la direzione della radiazione diffusa e quella della radiazione incidente, detto angolo di scattering, possiamo applicare il teorema di Carnot e scrivere:
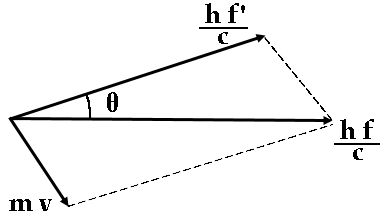
Ora, per il principio di conservazione dell'energia, si ha:
![]()
dove E è l'energia del fotone incidente ed E' quella del fotone diffuso. La precedente si può scrivere:
![]()
da cui possiamo ricavare:
![]()
La sostituisco nella (2.6) ed ottengo:
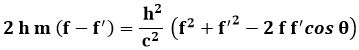
Ma f ed f ' differiscono molto poco tra di loro, per cui possiamo eseguire l'approssimazione:
![]()
Ne consegue:
![]()
Passiamo dalle frequenze alle lunghezze d'onda mediante la nota formula f = c / λ:
![]()
La possiamo riscrivere:
![]()
Chiamiamo Δλ = λ' – λ la variazione di lunghezza d'onda per effetto Compton. Dalla precedente ricaviamo allora:
![]()
Il termine h / m c ha le dimensioni di una lunghezza, come dimostra la seguente verifica dimensionale:
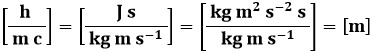
Tale termine viene chiamato lunghezza d'onda Compton, e vale:
![]()
Tale valore è i perfetto accordo con l'esperienza, e verifica una volta di più la bontà dell'ipotesi dei quanti. Naturalmente ogni particella ha la sua lunghezza d'onda Compton: quella del protone, ad esempio, vale 1,32 · 10–15 m. Il Δλ massimo si ha per θ = 180°, il cosiddetto "back scattering", com'è logico, perchè in tal caso la perdita di energia è massima da parte del quanto di luce. Nel 1925 i tedeschi Walther Bothe (1891-1957) e Hans Wilhelm Geiger (1882-1945) dimostrarono che fotoni ed elettroni sono emessi simultaneamente nell'effetto Compton. Se gli elettroni sono fortemente legati nella materia, lo scattering Compton è relativamente debole, ma per raggi X duri (cioè molto energetici) esso diviene la principale causa di attenuazione e diffusione della radiazione nella materia; ne deve tenere conto accuratamente chi progetta degli schermi antiradiazioni per impianti nucleari o per centri di medicina nucleare.
Prima di cambiare paragrafo, una curiosità che mi è stata suggerita da un mio studente. Osservate i tre famosi personaggi di "Star Wars" rappresentati qui sotto: chi dei tre è il più pericoloso? (attenzione: dovete rispondere usando gli strumenti della Fisica)



Se state per rispondere Darth Vader, sono costretto a contraddirvi: il più pericoloso è il famoso Jedi Mace Windu, interpretato da Samuel L. Jackson. Infatti imbraccia una spada laser di colore viola, e i fotoni corrispondenti al colore viola sono quelli con la frequenza maggiore; quindi, come ci ha insegnato Planck con la relazione E = h f, quelli di energia maggiore! La spada laser di Darth Vader è la meno pericolosa di tutte, perchè i fotoni corrispondenti al colore rosso sono quelli di frequenza minore e quindi di energia minore, tra i tre personaggi sopra riportati. Ne consegue che il celeberrimo duello tra Darth Vader e il suo maestro Obi-Wan Kenobi nel primo film della saga in ordine cronologico avrebbe dovuto essere vinto facilmente dal secondo (ma allora, dove andrebbe a finire l'epico scontro tra Darth Vader e suo figlio Luke Skywalker?)
.
A questo punto, sento già la vostra domanda: che relazione ha tutto questo, con i modelli atomici di cui abbiamo parlato nel primo capitolo? A questa domanda risponderemo nel capitolo seguente. Se volete tornare all'indice, invece, il link è questo.
