

|
"Penso si possa tranquillamente affermare che nessuno capisce la meccanica quantistica." Richard P. Feynman |
.
6.1 Una nuova equazione
Come preannunciato, questo capitolo richiede conoscenze avanzate di Analisi Matematica ed è riservato a chi è in grado di maneggiare tali strumenti; chi non lo è, passi direttamente al capitolo successivo. Del resto, il problema di trovare la funzione d'onda di un sistema quantistico è tutt'altro che semplice da risolvere. Come si fa a determinare il moto di una particella classica? Si risolve l'equazione rappresentata dal Secondo Principio della Dinamica o Equazione di Newton:
![]()
Analogamente, Erwin Schrödinger dimostrò che tutte le funzioni d'onda sono integrali particolari di un'equazione differenziale alle derivate parziali, oggi nota per l'appunto con il nome di Equazione di Schrödinger. Per derivarla, ricordiamo che tutti gli stati di moto di una particella sono combinazioni lineari delle equazioni di onde piane monocromatiche, del tipo:
![]()
dove si è posto:
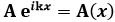
Come tutte le onde, la precedente obbedisce alla cosiddetta Equazione di D'Alembert, che prende il nome da Jean-Baptiste Le Rond d'Alembert (1717-1783), tra i principali protagonisti dell'Illuminismo e coautore dell'"Encyclopédie":
In essa v è la velocità dell'onda, e si è introdotto l'operatore noto come laplaciano:
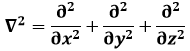
In una sola dimensione, essa coincide con la derivata seconda lungo x. Ora, poiché ω = 2 π f, si ha:
Imponiamo ora che l'energia e la quantità di moto siano scambiate in quantità discrete:
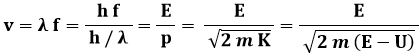
dove K = p2 / 2 m è l'energia cinetica ed U è l'energia potenziale. In definitiva:
Sostituisco la seconda delle (6.2) e la (6.3) nella (6.1) ed ho:
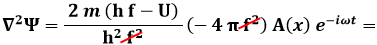
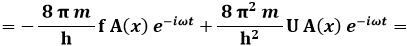
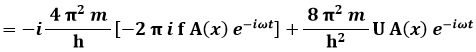
e introducendo la costante di Dirac h / 2 π si ha:
Questa è un'equazione di importanza universale, esattamente come l'equazione di Newton o le equazioni gravitazionali di Einstein, perchè tutti i sistemi quantistici sono sue soluzioni particolari. Erwin Schrödinger la pubblicò nel 1926 sugli "Annalen der Physik" nell'articolo « Quantisierung als Eigenwertproblem (Erste Mitteilung) », cioè « Quantizzazione come problema agli autovalori (prima comunicazione) ».

Erwin Schrödinger su una banconota austriaca da 1000 scellini
Si può intuire facilmente che è un'equazione difficilissima da risolvere. Portarla alle quadrature, cioè risolverla in modo analitico, è possibile solo in casi particolarissimi. Più in generale, sono possibili solo soluzioni numeriche. Nonostante questa difficoltà, si può affermare che tutta la Fisica Atomica, tutta la Fisica Nucleare, tutta la Fisica Molecolare, tutta la Fisica dello Stato Solido rappresentano tentativi di risolvere in modo opportuno l'equazione di Schrödinger!
In tre dimensioni, la funzione d'onda è del tipo Ψ = Ψ (x, y, z, t), e |Ψ|2 rappresenta la densità di probabilità di trovare la particella nel parallelepipedo [ x ; x + dx ] x [ y ; y + dy ] x [ z ; z + dz ]. Deve valere anche la condizione di normalizzazione:
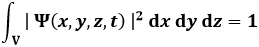
Per risolvere un'equazione differenziale occorrono delle condizioni. In particolare, occorrono le condizioni al contorno, dette anche B.C. (Boundary Conditions):
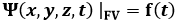
con f (t) nota, dove con FV si intende la frontiera del dominio V. Inoltre, necessitano anche le condizioni iniziali, dette anche I.C. (Initial Conditions):
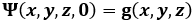
f (t) e g (x, y, z) vanno trovate mediante misure, oppure attraverso opportune ipotesi. Usando le B.C. e le I.C. è possibile definire come varia la Ψ nello spazio e nel tempo, cioè l'evoluzione del sistema quantistico. Ora, il teorema di Cauchy-Kovalevskaja, dimostrato da Augustin-Louis Cauchy (1789-1857) e Sofja Vasilevna Kovalevskaja (1850-1891), ci dice che, a partire da precise B.C. e I.C., un'equazione differenziale alle derivate parziali restituisce una soluzione ed una sola; dunque, l'evoluzione del sistema è di tipo deterministico. Questo ci può lasciare perplessi, perchè la Ψ ha piuttosto un significato probabilistico. Non bisogna però confondere il senso fisico della Ψ con la sua evoluzione: la distribuzione statistica delle particelle quantistiche evolve in modo deterministico. È solo l'ennesimo paradosso del mondo quantistico.
Inoltre, come anticipato nel capitolo precedente, l'equazione (6.4) è lineare, e quindi una combinazione lineare delle sue soluzioni è ancora una sua soluzione. Questo è noto come Principio di Sovrapposizione degli Stati., e il suo carattere paradossale ha portato al mito del Gatto di Schrödinger, noto per sentito dire anche a chi è del tutto digiuno di Meccanica Quantistica, del quale abbiamo già parlato ampiamente.
L'equazione (6.4) è un'equazione parabolica, e cioè, a differenza di quella di Laplace, non ammette soluzioni che si propagano inalterate nello spazio, a meno che U = 0. Inoltre, la presenza dell'unità immaginaria fa sì che le Ψ siano, in generale, funzioni a valori complessi; ciò conferma il fatto che Ψ non descrive alcuna grandezza fisica, altrimenti dovrebbe essere reale.
L'equazione muta forma a seconda del campo di forze F (r) che agisce sulla particella; tale informazione è contenuta nell'energia potenziale U, perchè:
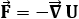
.
6.2 Gli stati stazionari
L'equazione di Schrödinger si può scrivere in una forma compatta, detta forma operatoriale, se introduciamo il cosiddetto operatore hamiltoniano:
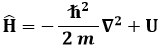
dove U è un fattore moltiplicativo. Allora la (6.4) si può riscrivere:
La Meccanica Quantistica si può riscrivere TUTTA in termini di operatori (la formulazione detta Meccanica degli Operatori); e siccome anche le matrici, se applicata ai vettori, sono degli operatori, se ne conclude che aveva ragione Gamow, quando diceva che sia la meccanica matriciale sia la meccanica ondulatoria costituiscono diverse descrizioni matematiche della stessa realtà!
Domanda: esistono funzioni d'onda il cui modulo quadrato non dipende dal tempo? Per rispondere, vediamo se è possibile disaccoppiare la dipendenza spaziale da quella temporale, scrivendo Ψ come il prodotto di una funzione della sola x con una della sola t:
ψ(r) si dice funzione d'onda spaziale. Si osserva che l'operatore hamiltoniano "lavora" solo sulle variabili spaziali, mentre la derivata spaziale a secondo membro della (6.5) opera solo sul tempo. Sostituisco la (6.6) nella (6.5) ed ho:
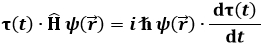
Infatti τ è costante rispetto ad r, e ψ lo è rispetto a t. Siccome τ dipende solo dal tempo, la derivata al secondo membro non è parziale, ma totale, e si può scivere τ'(t). Ho allora:
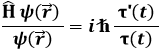
Abbiamo così separato le variabili! A sinistra ho una funzione della sola r, a destra una della sola t. Esse però sono identicamente uguali; ciò può accadere solo solo se sono entrambe costanti. Le porremo uguali alla costante di separazione E. Ho così due equazioni distinte, di cui la seconda è:
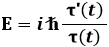
Separo le variabili ed ho subito:
Dunque, la dipendenza dal tempo della Ψ è esponenziale immaginaria. Poiché l'onda piana monocromatica è del tipo:
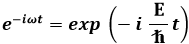
se ne deduce che, nella (6.7), la costante E rappresenta l'energia totale della particella. La (6.6) ha allora la forma:
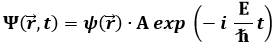
con A costante, e quindi, per nota proprietà dell'esponenziale immaginario:
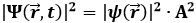
Il modulo quadrato è indipendente dal tempo; queste funzioni d'onda si dicono stati stazionari. Beninteso, le particelle non sono ferme, però la loro evoluzione non cambia nel tempo. Possiamo così finalmente capire perché l'elettrone non perde energia sulle orbite di Bohr: l'elettrone nell'atomo si muove in modo che le sue proprietà statistiche siano stazionarie! Quelle che nel modello quantomeccanico di Bohr-Sommerfeld erano le orbite quantizzate, delle quali nessuno capiva il perché fossero quantizzate, nel modello quantistico diventano gli stati stazionari dell'equazione di Schrödinger per l'atomo di idrogeno!
Questi stati stazionari hanno funzioni d'onda indipendenti dal tempo, fornite dall'altra delle due equazioni disaccoppiate:
detta equazione di Schrödinger per gli stati stazionari. Anche questa è lineare, ed è anche omogenea. Infatti ammette sempre la soluzione identicamente nulla, che però non soddisfa la condizione di normalizzazione. Ammette soluzioni diverse da quella nulla solo in corrispondenza di particolari valori discreti di E, detti autovalori dell'energia. Le equazioni come la (6.8) si dicono equazioni agli autovalori, e l'insieme degli autovalori costituisce lo spettro dell'operatore Ĥ. Essendo discreti, i valori di E si possono etichettare con un numero intero n, che prende il nome di numero quantico. Ad ogni autovalore corrisponde una o più soluzioni della (6.8), dette autofunzioni o autostati. Anch'essi sono etichettati dal numero quantico n, per cui si può scrivere:
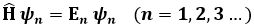
Se ad un solo autovalore En sono associati più autostati ψn, si parla di stati degeneri, e sono caratterizzati dal fatto di avere tutti la stessa energia, e cioè la stessa posizione nello spettro. Si può dimostrare che la degenerazione è sempre legata alle simmetrie del campo di forze considerato.
Siccome l'equazione agli autovalori ha solo soluzioni discrete, ne discende che la quantizzazione dei livelli energetici di un sistema quantistico emerge in maniera naturale dall'equazione di Schrödinger, cioè dalla stessa ipotesi ondulatoria, né è scindibile da questa. Ne segue che fisica atomica e fisica quantistica sono tutt'uno. E siccome anche una matrice ha autovalori ed autovettori, come ci insegna l'algebra matriciale, si scopre un nuovo punto di contatto tra la meccanica di Schrödinger e quella di Heisenberg. Cercare gli autostati di un sistema quantistico significa risolvere un problema agli autovalori. Dunque, le grandezze fisiche sono quantizzate semplicemente perché l'equazione a cui obbediscono è un'equazione agli autovalori, cioè ammette soluzioni non nulle solo in corrispondenza di particolari valori di quei parametri!

Il gatto di Schrödinger in carne ed ossa, grazie ad uno studente spiritoso (:
.
6.3 La particella nella... scatola
Vediamo un'applicazione di quanto si è detto nei paragrafi precedenti: il caso della particella libera, cioè non soggetta a forze. Insomma, quella con U = 0. Allora l'equazione di Schrödinger degli stati stazionari si riduce a:
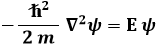
cioè, nel caso monodimensionale:
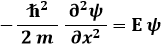
Una possibile soluzione di questa equazione è l'onda piana monocromatica:
Sostituendo nella precedente ho:
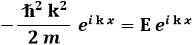
che è identicamente verificata, perchè le equazioni di de Broglie ci dicono che:
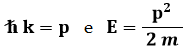
Gli autovalori dell'energia risultano allora:
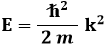
Se vario k con continuità, anche E varia con continuità. Inoltre, la (6.9) non è normalizzabile, perchè:
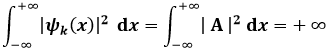
Su queste basi non si può studiare il caso di una particella libera. È però possibile studiare il caso della particella libera intrappolata in una scatola di ampiezza L, come in figura:
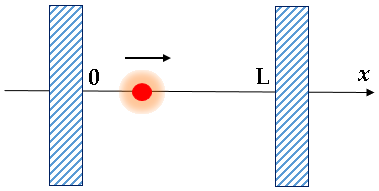
La particella è costretta ad andare avanti e indietro tra due pareti rigide. Posso allora imporre le semplici condizioni al contorno:
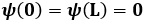
perché allora, nei punti x = 0 ed x = L, la particella incontra delle forze intensissime (al limite, infinite), causate dalla buca di potenziale perfettamente rettangolare, che la costringono a fermarsi e a tornare indietro. Questa situazione prende il nome di buca di potenziale, e la si può utilizzare per schematizzare varie situazioni fisiche, dall'elettrone intrappolato dentro l'atomo al protone intrappolato dentro il nucleo. In pratica, l'aspetto di questo potenziale sentito dall'elettrone nella buca è:
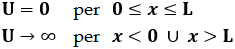

Più in generale, scriviamo la soluzione (6.9) nella forma:
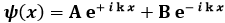
Essa verifica univocamente l'equazione di Schrödinger per la particella libera, come si verifica dopo immediata sostituzione. Sostituiamo in essa x = 0:
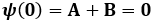
da cui B = – A. Ne ricaviamo:
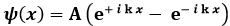
Moltiplicando e dividendo per 2 i, e poi chiamando 2 A i = C, si ha:
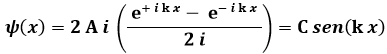
Ricordiamo che ψ non ha immediato significato fisico, per cui A, B e C possono essere anche numeri complessi. Come si vede, questa è un'oscillazione non smorzata. Sostituiamo allora ed imponiamo che ψ(L) = 0:
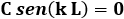
Questa è verificata se sen (k L) = 0, cioè se:
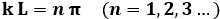
Ma k = 2 π / λ; ne segue che questa condizione si verifica se:
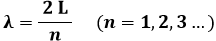
Ma queste sono le lunghezze d'onda di onde stazionarie intrappolate in una scatola. Dunque, il problema della particella libera in una buca di potenziale infinita equivale a quello delle oscillazioni di una corda vincolata agli estremi. Qui sotto vedete alcuni dei nostri autostati:
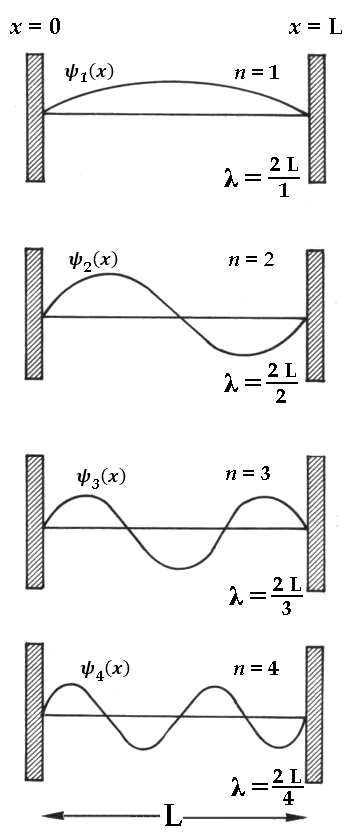
Da questi grafici è possibile ricavare quelli delle corrispondenti densità di probabilità di trovare l'elettrone. Ecco per esempio l'aspetto di quella per n = 3:
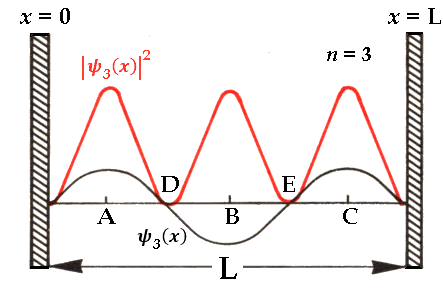
Come si vede, le "traiettorie" delle particelle quantistiche somigliano incredibilmente ad onde come noi le intendiamo. I corrispondenti autostati sono:
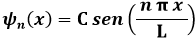
e i corrispondenti autovalori dell'energia risultano:
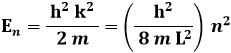
Rappresentandoli in funzione di n, si ottiene il grafico qui sotto:
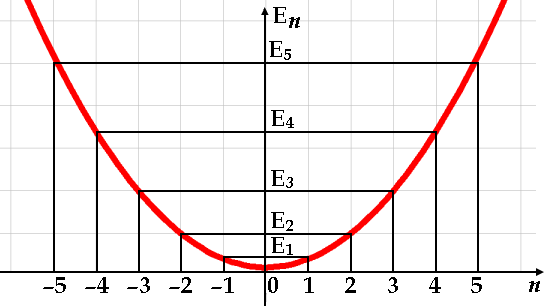
Si può osservare come gli autovalori dell'energia risultino due volte degeneri, giacché la stessa energia è posseduta da DUE diverse onde piane monocromatiche: e+ikx ed e–ikx. Come detto, tutto questo vale nel caso monodimensionale; di ciò che accadrebbe nel caso tridimensionale parleremo tra poco. Ora esaminiamo un altro problema che ci condurrà a delle conclusioni sconcertanti, se mai ci può creare ancora sconcerto qualcosa in un guazzabuglio come quello in cui ci siamo gettati a capofitto!
.
6.4 L'effetto tunnel
Discutiamo ora un problema più complesso, e cioè quello della particella in modo in una regione di spazio dove si trova un gradino di potenziale come quello in figura:
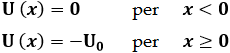
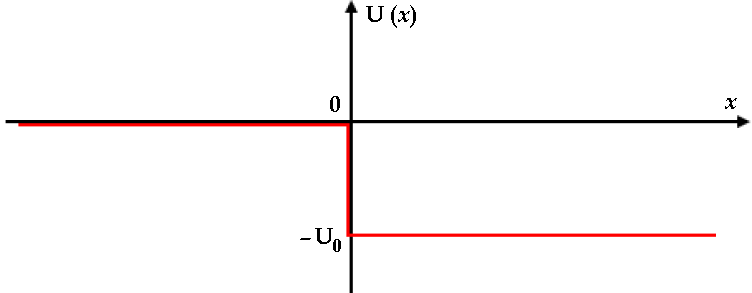
Evidentemente il problema andrà suddiviso in casi. Da un punto di vista classico, sono possibili tre situazioni diverse:
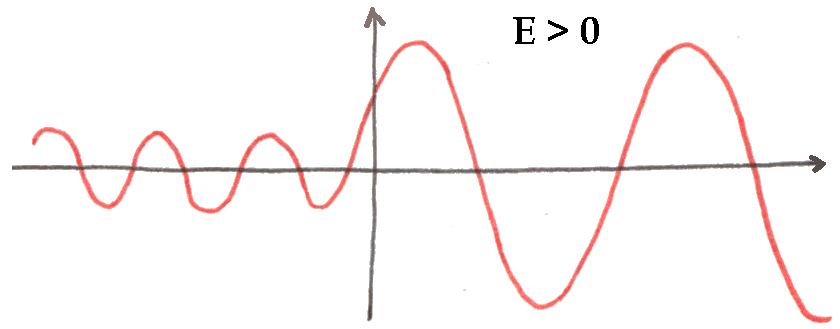
a) E > 0. Allora la particella trasla da – ∞ a + ∞, e si limita a cambiare velocità quando passa attraverso l'origine, "sentendo" un diverso potenziale dalle due parti.
b) – U0 < E < 0. Allora l'elettrone può muoversi solo da 0 a + ∞; non può muoversi nella regione negativa, perché lì l'energia cinetica sarebbe negativa.
c) E < – U0. In questo caso il moto non è possibile in nessuna regione dello spazio.
Vediamo ora di affrontare lo studio del medesimo problema dal punto di vista quantistico, imponendo una funzione d'onda ψ(x) del tipo:
a) Sia anzitutto E > 0. L'equazione di Schrödinger per x < 0 è la solita:
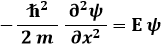
mentre per x > 0 diventa:
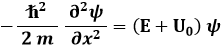
perchè qui U = – U0. In esse dobbiamo sostituire le (6.10). Per semplificare le cose, però, chiameremo:
A+ = 1 ; A– = ρ ; B+ = τ ; B– = 0
ρ si dice coefficiente di riflessione, e τ coefficiente di trasmissione; infatti l'onda piana monocromatica verrà in parte riflessa e in parte trasmessa. Otteniamo così:
È evidente che la (6.11) e la (6.12) devono raccordarsi tra di loro con continuità, ma devono raccordarsi tra di loro anche le rispettive derivate prime. Deve cioè risultare:
ψ (0–) = ψ (0+)
ψ ' (0–) = ψ ' (0+)
Otteniamo così il sistema:
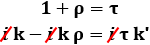
da cui si ricava:
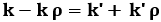
e quindi:

Rappresentando le (6.11) e (6.12) si ottiene il diagramma sottostante. Si osservi che, se k → 0 (cioè se λ → ∞), ρ → – 1 e τ → 0. Allora, tutta l'onda viene riflessa e nulla viene trasmesso.
b) Consideriamo ora il caso con – U0 < E < 0. In tale situazione, noi sappiamo che:
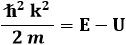
per cui:
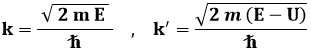
Se E < 0, k è immaginario, mentre k' è reale. Chiamiamo:
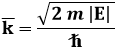
per cui:
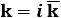
Sostituisco nelle mie due equazioni e trovo facilmente:
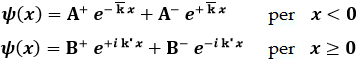
Ma noi sappiamo che entrambe le funzioni d'onda devono essere normalizzate, e la condizione affinché ciò avvenga è che non divergano. Deve dunque essere:
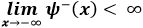
Ora, si ha certamente:
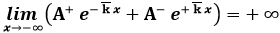
a meno che non risulti A+ = 0. Imposta questa condizione, le suddette equazioni diventano:
Anche queste, come le precedenti, devono raccordarsi in x = 0 assieme alle loro derivate prime. Il sistema che si imposta stavolta è:
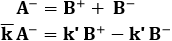
da cui:

e dunque:
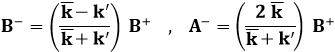
Rappresentando le (6.13) e (6.14) da noi calcolate si ottiene l'andamento seguente:
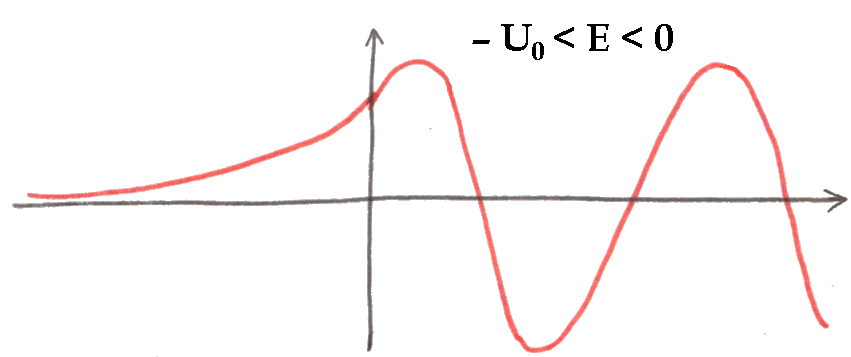
c) Sia infine E < – U0. È allora possibile verificare che, in questo caso, Meccanica Classica e Meccanica Quantistica sono d'accordo nell'affermare che non vi è alcun moto da parte della particella.
In teoria, anche nel caso b) il moto non dovrebbe essere possibile, se ci trovassimo nel mondo classico; e invece, ecco che la particella quantistica può penetrare la buca di potenziale, e può muoversi anche in regioni "proibite" nel caso classico. È come se io tirassi una palla da basket contro il muro: nella Fisica Classica, la palla ha il 100 % di probabilità di rimbalzare indietro, e lo 0 % di attraversarlo. Al contrario, nella Meccanica Quantistica la palla ha una probabilità, per quanto piccola, di attraversare il muro! Questo strano fenomeno prende il nome di effetto tunnel, ed è una caratteristica precipua delle particelle quantistiche. Lo si vede esemplificato in questa vignetta (tratta da questo sito):

È importante osservare che, per il Principio di Indeterminazione di Heisenberg, non è mai possibile osservare una particella mentre attraversa la barriera di potenziale, ma solo prima e dopo tale transizione. L'effetto tunnel fu introdotto per la prima volta nel 1928 dal fisico statunitense Julius Robert Oppenheimer (1904-1967), meglio noto al grande pubblico (soprattutto dopo l'uscita nel 2023 del film di Christopher Nolan a lui dedicato) per i contributi dati al Progetto Manhattan per la realizzazione della prima bomba atomica, del quale fu direttore. L'idea fu poi ripresa e sviluppata dal fisico ucraino George Gamow (1904-1968) in un articolo pubblicato pochi mesi dopo la prima ipotesi di Oppenheimer, e dagli americani Ronald Gurney (1898-1953) ed Edward Condon (1902-1974): i tre elaborarono indipendentemente l'uno dall'altro un modello per spiegare l'emissione di particelle alfa da parte di un nucleo atomico pesante (qui un approfondimento) e la loro penetrazione in un nucleo leggero, causando una trasmutazione nucleare. Sia il nucleo che la particella alfa hanno carica positiva, per cui dovrebbero respingersi reciprocamente; dunque appare assai difficile portarli a distanza tale (dell'ordine delle dimensioni nucleari) da farli interagire tra loro. Quanto alle particelle alfa che si trovano dentro il nucleo, ad esse viene impedito di sfuggire dalle forze nucleari, 100 volte più intense della repulsione coulombiana. Sia le forze elettromagnetiche per le particelle in entrata nei nuclei, che quelle nucleari forti per le particelle in uscita, costituiscono proprio delle barriere di potenziale, analoghe a quelle che abbiamo appena studiato. Eppure si osservò che alcuni elementi radioattivi (radio, torio, uranio) espellono tranquillamente delle particelle α, nonostante la loro energia cinetica sia molto inferiore a quella necessaria per scavalcare la barriera. Idem per le particelle α "sparate" contro i nuclei con energia cinetica inferiore a quella necessaria per superare la barriera di potenziale, che invece possono tranquillamente penetrare nei nuclei e dare vita a radioattività artificiale. Entrambi i processi sarebbero impossibili dal punto di vista classico; essi dunque sono spiegabili solo ipotizzando che l'onda di de Broglie associata alle particelle α venga in parte riflessa e in parte trasmessa per effetto tunnel! In realtà non è la particella a "disintegrarsi" e a venire in parte riflessa e in parte trasmessa, ma è la densità di probabilità di trovarla a suddividersi. Le α hanno cioè una probabilità di essere riflesse e un'altra di penetrare nel nucleo (o di lasciarlo), in accordo con l'interpretazione probabilistica di Max Born da noi esposta nel § 5.5! Tuttavia, il contributo iniziale dato da Oppenheimer è spesso sottovalutato (se non proprio omesso) nella maggior parte dei libri di testo, a vantaggio di Gamow, Gurney e Condon, ed è per questo che mi preme sottolinearlo.
In seguito proprio Max Born (1882-1970) comprese che l'effetto tunnel non è esclusivo della Fisica Nucleare, ma si presenta anche in molti altri fenomeni fisici. Qui sotto potete vedere una simulazione dell'evoluzione della funzione d'onda di un elettrone che in parte si riflette e in parte filtra attraverso una barriera di potenziale, realizzata dal francese Jean-Christophe Benoist:
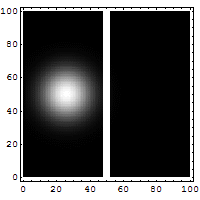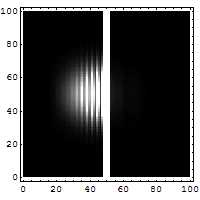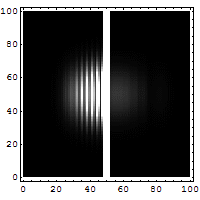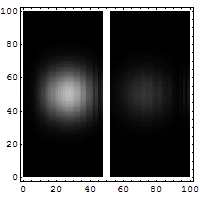
Sebbene l'effetto tunnel sia estremamente controintuitivo e appaia addirittura paradossale (come può una palla da basket attraversare il muro contro cui è scagliata?), esistono innumerevoli prove sperimentali a sostegno della sua esistenza, in primis l'orbitale 2p dell'atomo di idrogeno, in cui l'elettrone sembra passare "attraverso" il nucleo. Inoltre, se avviciniamo due atomi a formare una molecola, un elettrone di valenza inizialmente legato al primo atomo può, di punto in bianco, ritrovarsi a ruotare attorno al secondo, proprio per effetto tunnel.
Allo stesso fenomeno è dovuto il decadimento radioattivo che si manifesta attraverso la fissione spontanea. Inoltre, senza l'effetto tunnel, le temperature presenti nei nuclei delle stelle non sarebbero sufficienti a innescare le reazioni nucleari che le fanno brillare; in altre parole, il nostro Sole brilla proprio grazie all'effetto tunnel. E non è tutto: come si legge in questo articolo, nel settembre 2013 Robert J. Shannon dell'Università di Leeds è riuscito a spiegare in laboratorio la possibilità di formazione di molecole di alcool, come il radicale metossile (CH3O) rilevato nello spazio interstellare, mediante l'effetto tunnel. Nel 2023, poi, Roland Wester dell'Università di Innsbruck e colleghi sono riusciti a individuare l'effetto tunnel quantistico in quella che la fisica classica riterrebbe una reazione impossibile tra molecole di idrogeno e ioni deuterio. È stata la prima conferma sperimentale di una previsione teorica sul tasso di effetto tunnel in una reazione chimica che coinvolge ioni. Anche molti dispositivi elettronici, come i diodi tunnel e il microscopio elettronico ad effetto tunnel, sfruttano questo effetto per il loro funzionamento.
.
6.5 Condizioni periodiche al contorno
Torniamo ora al problema della particella libera nello spazio infinito, e proviamo ad imporle quelle che vengono chiamate le condizioni periodiche al contorno di Born-von Kármán, da nomi del già citato Max Born e del matematico ungherese Theodore von Kármán (1881-1963):
ψ (x + L) = ψ (x)
Ciò vuol dire che, sulla superficie di equazione x = L, la situazione è identica a quella che si verifica sulla superficie con x = 0. Questo è il trucco che si applica nei vecchi videogiochi, quando un personaggio sparisce sul lato destro del teleschermo e riappare sul lato sinistro, come se si muovesse in modo continuo. In pratica, è come se dividessimo lo spazio in tante cellette, nelle quali si ripete all'infinito la medesima situazione: se una molecola esce da una faccia, un'altra rientra dalla faccia opposta.
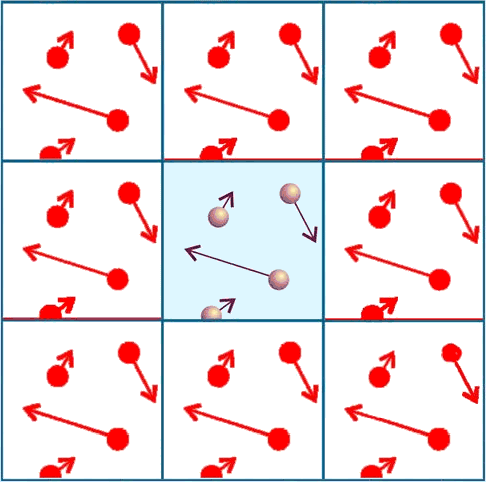
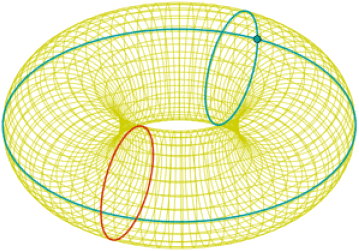
Nel caso monodimensionale, ciò si verifica lungo una circonferenza, perchè dopo ogni giro si ripete identica la stessa situazione. In due dimensioni, invece le condizioni periodiche al contorno sono verificate sulla superficie di un solido chiamato toro, ottenuto dalla rotazione di una circonferenza intorno ad una retta che non la attraversa (la parola "torus" in latino indicava un cuscino a forma di ciambella). Il toro infatti può essere spazzato da due famiglie di circonferenze ortogonali tra di loro: alla fine di ogni giro in ciascuna direzione, si torna al punto di partenza. In tre dimensioni non esiste invece un modello geometrico in grado di esemplificare le condizioni al contorno periodiche.
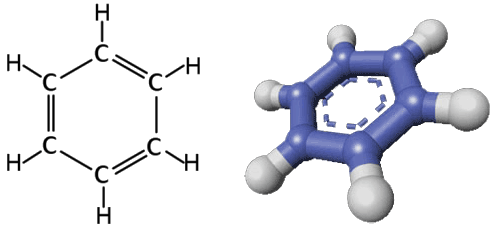
Questo sembra un discorso astratto, ed invece in Fisica Molecolare le condizioni al contorno periodiche sono molto utili: basta pensare alla molecola di benzene (C6H6), che è chiusa ad anello. Gli elettroni al suo interno si possono muovere lungo questo anello, risultando quasi liberi. Anche i solidi sono ritenuti di dimensioni infinite, perchè sono molto più grandi delle singole molecole che li compongono, per cui la condizione di applicabilità delle condizioni periodiche al contorno di Born-Von Kármán è perfettamente soddisfatta, e dunque è comodo introdurle per studiare la struttura elettronica dei cristalli.
In tre dimensioni, le condizioni periodiche al contorno diventano:
ψ ( x + L, y, z ) = ψ ( x, y, z )
ψ ( x, y + L, z ) = ψ ( x, y, z )
ψ ( x, y, z + L ) = ψ ( x, y, z )
e l'onda monocromatica ha equazione:
![]()
Sostituendola nelle precedenti si ha:
exp ( i kx x ) = exp [ i kx ( x + L )]
exp ( i ky y ) = exp [ i ky ( y + L )]
exp ( i kz z ) = exp [ i kz ( z + L )]
da cui:
exp ( i kx L ) = exp ( i kx L ) = exp ( i kx L ) = 0
Il che implica:
kx L = 2 π nx
ky L = 2 π ny
kz L = 2 π nz
dove nx, ny, nz sono tre numeri quantici. Abbiamo così:
![]()
e quindi:
![]()
dove i, j, k sono i versori dei tre assi. Ogni volta che nx, ny, nz aumentano di 1, k subisce le seguenti variazioni:
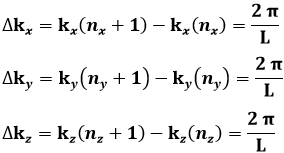
Quindi Δkx, Δky, Δkz sono inversamente proporzionali allo spigolo L della cella elementare. Anche k descrive dunque un reticolo regolare, quando x descrive le "celle" in cui abbiamo periodizzato lo spazio, per cui si parla di reticolo reciproco. Mentre il passo del reticolo diretto è L, quello del reticolo reciproco è 2 π / L. Se L → ∞, 2 π / L → 0, e si ritorna nella situazione di particella libera da – ∞ a + ∞ e spazio continuo.
Esempio di gif animata in cui la pallina azzurra
scompare a sinistra e ricompare a destra, e viceversa!
Ora impongo la normalizzazione nella cella di volume L3. Poiché:
![]()
devo imporre |A|2 L3 = 1, per cui:
![]()
Si ha così:
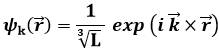
e gli autovalori dell'energia risultano:
![]()
perché:
![]()
In una sola dimensione, otteniamo:
![]()
Se rappresentiamo En in funzione di n, si osserva che En è lo stesso per n = n e per n = – n. Ciò significa che questi stati sono due volte degeneri, perchè la stessa energia è posseduta da due diverse onde piane monocromatiche, cioè e+ikx ed e–ikx. In tre dimensioni, avrebbero la stessa energia tutti gli stati che si trovano su di una superficie sferica nello spazio ( nx, ny, nz ). C'è un solo stato non degenere, quello corrispondente ad energia nulla.
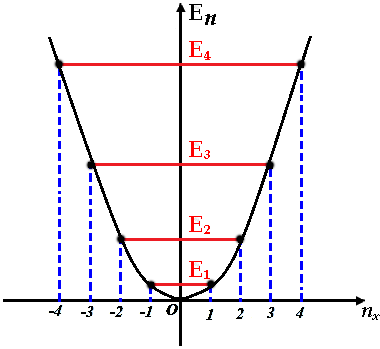
Le righe rosse nella figura soprastante rappresentano lo spettro energetico della mia particella confinata nella scatola. È facile verificare che le onde così costruite sono stazionarie; a k = ( 2 π / L ) n corrisponde infatti λ = L / n, per cui la lunghezza d'onda delle onde piane monocromatiche è sempre un sottomultiplo intero della lunghezza della scatola!
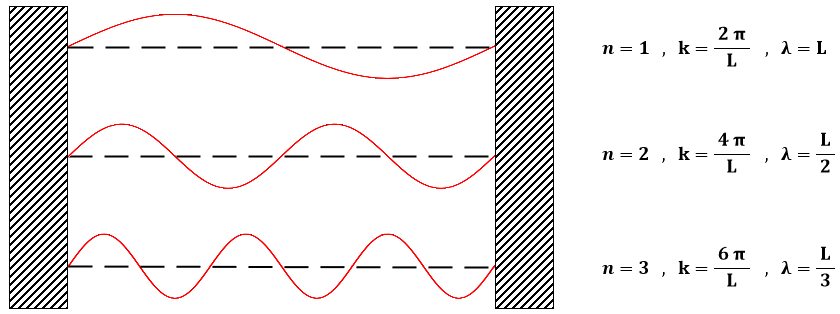
.
6.6 Il pendolo quantistico
I casi che abbiamo esaminato finora prendevano tutti in considerazione dei potenziali costanti a tratti. Vogliamo concludere questo capitolo mostrando un esempio, peraltro famosissimo, di potenziale non costante: quello dell'oscillatore armonico quantistico. Il potenziale è del tipo:
![]()
 Nell'ambito della Fisica Classica, basta applicare
l'equazione di conservazione dell'energia:
Nell'ambito della Fisica Classica, basta applicare
l'equazione di conservazione dell'energia:
Ec + U = E cost.
cioè:
![]()
derivando ambi i membri, e ricordando che la derivata rispetto al tempo della velocità è l'accelerazione, cioè la derivata seconda dello spostamento rispetto al tempo, si ottiene:
![]()
Questa è l'equazione dei moti armonici. Com'è ben noto, il suo integrale generale è:
![]()
dove:
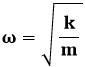
Tale moto è quello di una massa vincolata elasticamente ad una molla di costante elastica k, che perciò oscilla intorno ad un punto fisso lungo l'asse x. Si osservi che il potenziale in questione è di forma parabolica, e a sua volta rappresenta una buca di potenziale, anche se non di forma rettangolare, a differenza del caso visto nel § 6.3. Si tratta di una buca di potenziale parabolica, e dunque la sua ampiezza cresce al crescere dell'energia.
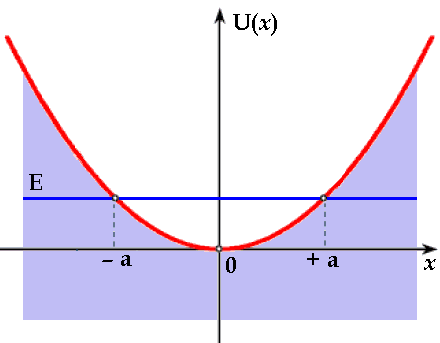
Da un punto di vista classico, il moto si può studiare anche ricordando che l'energia cinetica deve essere necessariamente positiva, e quindi deve necessariamente risultare E > U. Fissato un livello E di energia, si ha il moto in senso classico solo tra – a e + a. Questi due punti, dove la velocità si annulla e cambia verso, si dicono punti di inversione o di riflessione. Invece, nel caso quantistico ci aspettiamo ovviamente un effetto tunnel. L'equazione di Schrödinger in questo caso diventa:
Ovviamente ci riferiamo sempre al caso monodimensionale. Come si vede, il secondo termine dipende da x, e dunque non potremo più trovare una soluzione del tipo e± i k x. Come risolvere questa complicata equazione?
L'idea è quella di operare un cambio di coordinate, ponendo:
![]()
con α da determinare. Allora si ha:
![]()
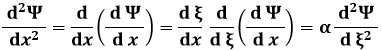
La (6.15) diventa allora:
![]()
cioè:
pongo ora:
![]()
Per ottenere questo risultato, deve aversi:
![]()
Le sue dimensioni fisiche sono:
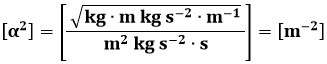
Dunque α è l'inverso di una lunghezza, per cui ξ è una variabile adimensionale. Introduciamo adesso:
![]()
In analogia con il caso classico, si è posto:
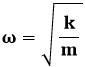
Poiché h ω è un'energia, anche ε è adimensionale. Allora la (6.16) diviene:
Questa è un'equazione adimensionale, detta equazione di Hermite-Schrödinger, dal nome del matematico francese Charles Hermite (1822-1901). In forma operatoriale la si può riscrivere:
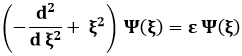
Analogamente alla (6.8), come i valori di E sono gli autovalori dell'operatore Ĥ, così i valori di ε sono gli autovalori dell'operatore di Hermite-Schrödinger, che è tra parentesi nella formula soprastante. Per risolvere questo rebus, un'idea geniale è la seguente. Osserviamo che, per ξ → ∞, la (6.17) ammette la cosiddetta soluzione asintotica:
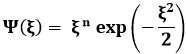
perché:
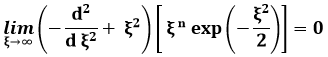
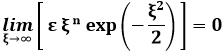
in quanto l'esponenziale prevale sempre sulle potenze di ξ. A questo risultato si può arrivare per via euristica (cioè non matematicamente rigorosa) ricordando che, nel caso del gradino di potenziale studiato sopra, ψ(x) diminuisce per x molto grande con andamento del tipo e– α x, dove:
![]()
Nel nostro caso, ad U va sostituita l'energia potenziale elastica:
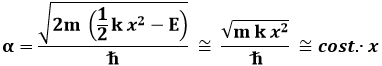
Dunque il decadimento deve ora essere del tipo exp (– α x2). Se allora sostituisco nell'equazione di Hermite-Schrödinger una soluzione del tipo:
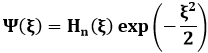
dove Hn(ξ) è un opportuno polinomio di grado n, ottengo un'equazione famosissima della Fisica Matematica, la cosiddetta equazione di Hermite:
Siccome le sue soluzioni non nulle sono dei polinomi, tentiamo una soluzione per serie:
Sostituendola nella (6.18) troviamo, come succede in questi casi, una relazione di ricorrenza tra i coefficienti della serie:
![]()
Noti a0 ed a1, possiamo trovare tutti i coefficienti della serie (6.19). Si osserva che, se a0 ≠ 0 e a1 = 0, avremo solo coefficienti pari non nulli, cioè Hn(ξ) è pari. Se invece a0 = 0 e a1 ≠ 0, avremo solo coefficienti dispari non nulli, cioè Hn(ξ) è dispari. Siamo perciò certi di avere due soluzioni linearmente indipendenti.
Ora dobbiamo cercare gli autovalori. Proviamo ad imporre εn = 2 n + 1. Allora:
![]()
Scegliamo una soluzione s con la stessa parità di n. Allora, a partire da as, tutti i coefficienti sono nulli. Ne segue che le (6.19) non sono più serie, bensì polinomi! Costruendo tali polinomi secondo la regola suddetta, si verifica che essi sono tali che:
![]()
Questi si dicono polinomi di Hermite. Osservando che vale la condizione di ricorrenza:
![]()
è possibile costruire i primi polinomi di Hermite:
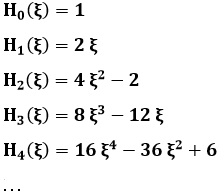
Effettivamente, essi hanno la stessa parità di n: quelli di posto pari sono pari, quelli di posto dispari sono dispari. Tuttavia le nostre soluzioni vanno normalizzate. Si può dimostrare che il risultato finale è allora:
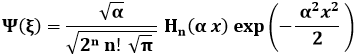
E gli autovalori dell'energia? Si ricavano da:
![]()
cioè:
![]()
Questo risultato è estremamente significativo. Come si vede, la frequenza delle oscillazioni è la stessa dell'oscillatore classico; quest'ultimo, però, poteva oscillare con tutte le energie che voleva. L'oscillatore armonico quantistico, invece, può oscillare solo per particolari valori dell'energia. Si osserva subito che i livelli energetici sono equispaziati, mentre quelli dell'atomo d'idrogeno si infittiscono al crescere dell'energia.
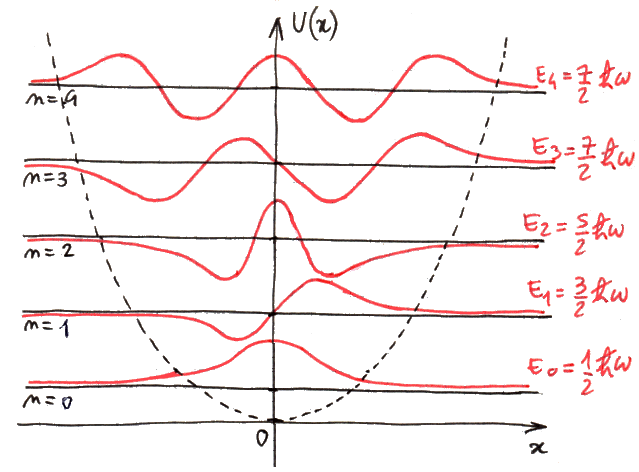
Come si vede dalla figura soprastante,disegnata a mano libera dall'autore di questo ipertesto, il primo livello energetico (per n = 0) non ha energia zero. Nell'oscillatore armonico classico è intuitivo che, ovviamente, l'oscillatore di energia minima è quello fermo nella posizione d'equilibrio. Ma nella Meccanica Quantistica questo fatto è inammissibile: se l'oscillatore fosse fermo con energia nulla, avrei che la quantità di moto sarebbe nulla ed anche x = 0, in completo disaccordo con il Principio di Indeterminazione.
L'energia non nulla del primo livello energetico si dice energia di punto zero. Il fatto che i livelli sono equispaziati è una caratteristica unica dell'oscillatore armonico quantistico. Tutto questo può sembrare solo un'applicazione accademica, ma in realtà l'oscillatore armonico quantistico sta alla base di tutto lo studio dello scambio di energia tra la radiazione e la cavità di un corpo nero, da noi discussa nel § 2.2. Infatti, il quanto fondamentale di energia che gli ipotetici oscillatori armonici armonici possono scambiare con la radiazione è:
![]()
cioè proprio l'ipotesi di Planck che è alla base di tutto lo studio che stiamo portando avanti da sei capitoli a questa parte!

Charles Hermite (Dieuze, 24 dicembre 1822 – Parigi, 14 gennaio 1901)
Prima di chiudere questo capitolo così complesso e specialistico, vorrei aggiungere che, se vogliamo applicare tutto quanto visto in esso all'atomo di idrogeno, nella (6.4) bisogna inserire l'espressione dell'energia potenziale elettrostatica prodotta dal nucleo. Otteniamo così l'equazione:
![]()
dove:
![]()
è la distanza dal nucleo. Nonostante le apparenze, tale equazione è davvero impegnativa, e richiede calcoli complicatissimi per essere risolta; tuttavia, a differenza di altri casi, è possibile portarla alle quadrature, cioè darne una soluzione rigorosa, non attraverso approssimazioni numeriche o simulazioni al computer. Risolvendo l'equazione di Schrödinger dell'atomo di idrogeno, è possibile ricavare su di esso tutto quanto già sappiamo a livello empirico, escluso lo spin, come vedremo nel capitolo 9. Il risultato più importante consiste nel fatto che, al posto delle orbite quantomeccaniche previste da Bohr e Sommerfeld, troveremo delle funzioni d'onda che obbediscono alle leggi di quantizzazione da noi già viste per l'energia, il momento angolare e il momento magnetico. Tali funzioni d'onda prendono il nome di orbitali, e rappresentano delle distribuzioni di probabilità, cioè delle zone dello spazio in cui è più probabile trovare l'elettrone. Proprio alla discussione di tali orbitali, sia atomici che molecolari, dedicheremo il capitolo successivo.
.
Se non vi ho stancato con questa lunga cavalcata attraverso l'Analisi Matematica, vi consiglio di cliccare qui e di passare con me al prossimo capitolo, nel quale vedremo come si costruiscono nell'ambito della Fisica Quantistica gli atomi degli elementi della tavola periodica. Per tornare all'indice, invece, il link è questo.
